浅析力学中能量守恒定律的作用与意义

蒋欣吕

摘 要：作为现代高中学生，我们要积极树立起能量守恒观念，不断增强运用能量守恒定律解题的主动性。能量守恒定律贯穿整个高中物理力学学习过程，分析与探讨它的作用与意义，以能量守恒为基点，能够帮助高中学生高效地解决各种力学难题。

关键词：力学；高中物理；能量守恒定律

中图分类号：G63 文献标识码：A 文章编号：1673-9132（2018）03-0027-02

DOI：10.16657/j.cnki.issn1673-9132.2018.03.015

能量守恒定律贯穿了整个高中物理力学学习内容，在经典物理学中具有广泛的应用。在高中力学内容中主要包括了三个能量守恒定律，分别是动能定理、功能定理以及机械能守恒定律。学习掌握好这些能量守恒定律内容，能够帮助高中生高效解决各种力学难题[1]。

一、力学中能量守恒定律解题的规律性作用

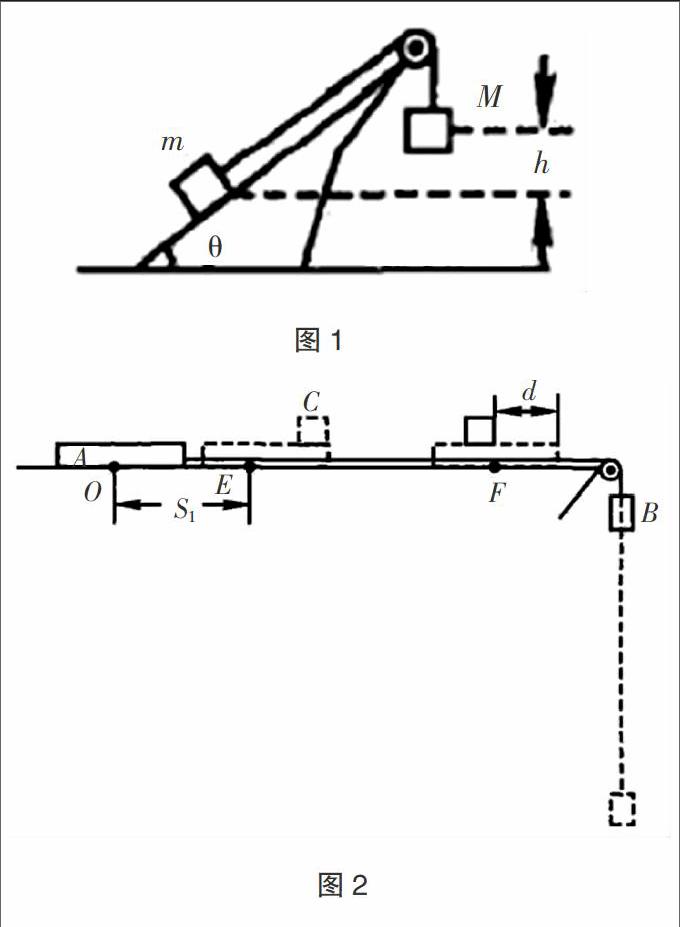
例1：如下图1所示，存在两个物体质量分别为m和M，使用不可伸长的非弹性轻绳将这两个物体有效连接起来，轻绳会跨过轻质无摩擦的定滑轮。其中m和斜面前的动摩擦因数为μ，斜面倾斜角为θ，在最开始这两个物体的高度差为h。如果在力的作用下，两个物体从静止开始运动，那么求出M落到m最初所在水平位置时的速度。

对于该题的解法，高中生可以利用能量守恒定律相关知识内容，将物体和地球作为力学系统，该系统的内力为M和m的重力。系统所受到的外力是斜面对m的支持力N以及滑动摩擦力f。根据图1可知，绳子对M做负功，对m做正功，对系统所做总功为0，等效不做功，所以可得只有f在做功。我们取m最开始所在水平面为重力势能参考平面，就能够得出该力学系统的末态机械能为[（M+m）v2/2+mghsinθ]。从初态到末态，机械能有效转化为内能的量值是μmghcosθ。根据物理能量守恒定律可得：Mgh=（M+m）v2/2+mghsinθ+μmghcosθ，最后解出M落到m最初所在水平位置时的速度v=[2Mgh-2mgh（sinθ+μcosθ）/（M+m）]1/2。

二、在力学中运用能量守恒定律解题的优越性

例2：如下图2所示，存在一块木板A质量mA=1kg，物体B质量也为1kg。在开始阶段通过用手托住物体B，木板A在O点处于静止状态，绳子则正好处于绷紧拉直状态。接着，放开托住物体B的手，让A、B进行加速运动，当木板A在水平桌面上滑过距离s1=1m至E点时，在该木板上轻缓地放上质量为mC=5kg的物体C，物体C相对于木板A后退距离d=0.5m后，与木板A相对静止而一起发生运动，最后在F点停止运动。已知物体C与木板A以及木板A与桌面间的动摩擦因素都为μ=0.2，那么求出点E与点F之间的实际距离。

我们可以使用能量守恒定律进行科学解题，将物体A、B、C和地球当做一个系统，在系统状态发生具体变化过程中，外力仅仅只有桌面对木板A的滑动摩擦力做功，而内力除了物体B的重力做功外，仅仅只有物体A与物体C之间的滑动摩擦力做功[2]。由于物体A与C的重力势能不会产生变化，我们可以将其设定为0，对物体B取其终止位置为重力势能零势能点。那么可知，该系统初始状态的机械能为E=mBg（s1+sEF），末态机械能则为E′=0，系统从初始状态到末状态的机械能向内能有效转化的量值为△E内=umAgs1+u（mA+mB）gsEF+umcgd。

根据能量守恒定律可得，E-△E内=E′，通过将E、E′以及△E内的表达公式分别带入到上面式子中，就可以得到SEF=1.5m。因为力学系统从初始状态到末状态机械能量的变化通常可用滑动摩擦力与相对位移的乘积简单的量度出来，所以通过使用能量守恒定律解该类型题目更加快捷方便，具有一定的优越性。

三、力学中能量守恒定律解题的高效性

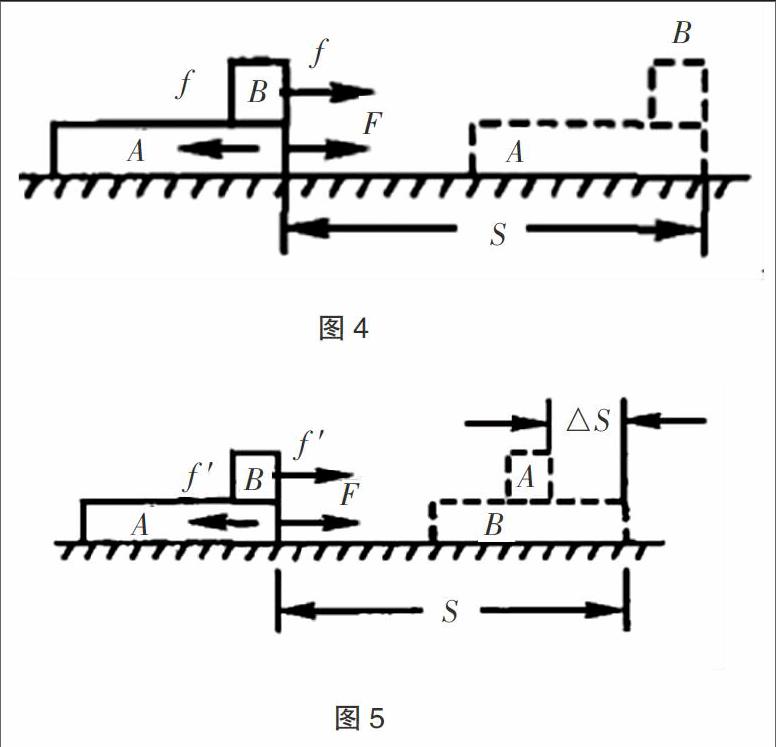
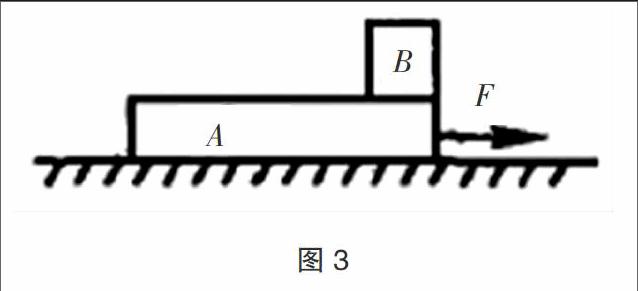
例3：如下图3所示，木板A静止在光滑的水平面上，在其上面的小木板B则放置在最右端。当给木板A一水平外力F时，木板A会随之产生位移s。第一次的外力F较小，木板B在木板A上不会发生相对滑动，它们两者之间的摩擦力为f；第二次的外力增大时，木板B在木板A上发生了明显的滑动，距离为△s，A和B之间的摩擦力为f′。那么基于这两种情况下，木板A与木板B系统动能的增量、能量的增量以及摩擦力对A、B系统做的总功为多少？

在第一种外力F较小的情形下，A、B水平方向的受力如下图4所示，其中f是静摩擦力，我们根据动能定理可知物体B动能增量为△EkB=fs，物体A的动能增量为△EkA=Fs-fs。A、B系统的动能增量为△Ek=△EkA+△EkB=Fs。

在第二种外力F较大的情形下，A、B之间的摩擦力f′是滑动摩擦力，如下图5所示，我们根据动能守恒定律可得，B动能增量为△EkB′=f′（s-△s），A的动能增量为△EkA′=Fs-f′s，A、B系统的动能增量为△Ek′=△EkA′+△EkB′=Fs-f′△s，最终得到Fs-△Ek′=f′△s。

在上式中，Fs是外界传递给A、B系统的能量，△Ek′则是A、B系统动能的增量。由于A、B系统出了动能量增加外，还会存在内能发生变化，比如滑动摩擦产生热量。根據能量守恒定律可得，Fs-△Ek′表示的是系统内能的实际增量，其准确数值等于f′△s。滑动摩擦力f′对物体B做正功为f′（s-△s），对物体A做负功为-f′s，最终得出对A、B系统做的总攻为Wf=f′（s-△s）-f′s=-f′△s。从这道题的解题过程中，我们得出以下结论：（1）外力所做的功是系统与外界能量交换的量度；（2）滑动摩擦力与受它作用的两物体之间的相对位移大小的乘积是机械能转化为内能的量度。高中生掌握该结论知识，有利于提高用能量守恒定律解题的效率和质量。

四、结语

综上所述，力学作为高中物理的重要组成部分，高中生要正确认识到其重要性，通过学习掌握到能量守恒定律知识内容，能够最大程度提升对力学题目的解题水平，培养自身良好的物理综合学习能力。

参考文献：

[1] 代娟娟.力学中三个能量守恒定律的应用[J].湖南中学物理，2009（10）.

[2] 付昱华.能量守恒定律为唯一源定律的新牛顿力学[J].前沿科学，2014（2）：74.endprint