蚁群遗传融合算法在移动机器人路径规划中的应用*

于树科，瞿国庆，祁宏宇，赵开新

（1.江苏商贸职业学院，江苏 南通 226011；2.河南工学院，河南 新乡 453002）

0 引言

路径规划是移动机器人导航领域研究的首要任务，也是机器人安全无碰撞地执行各项任务的基本保障，目前在移动机器人路径规划过程中经常使用的智能算法有蚁群算法、遗传算法、神经网络法、粒子群算法等［1］。针对传统蚁群算法在路径搜索初期存在盲目性，搜索空间大、效率较低，而遗传算法全局搜索方面的能力较强，但在搜索后期启发信息利用不足等缺陷［2］。本文融合蚁群和遗传算法，并把融合后的算法应用到移动机器人路径规划中。

1 蚁群和遗传算法分析

1.1 蚁群算法

蚁群算法（Ant Colony Algorithm，ACA）［3］是根据自然界中蚂蚁觅食行为而提出的一种模拟进化算法。算法中要求蚂蚁在搜索路径时不能重复经过同一节点，通过在算法中加入了禁忌表项来实现。表示第k只蚂蚁在t时刻的i节点选择向j节点移动的概率。

蚁群算法是一种求解组合最优路径问题的启发式方法，该算法具有分布式计算、正反馈机制和良好的并行性、健壮性和可扩展性，并且蚂蚁觅食行为与机器人路径规划有着天然的关联性，因此，可以被应用到移动机器人路径规划中。但该算法在搜索初期存在盲目性大，在搜索后期存在着耗时长和容易出现停滞等缺陷。因此，传统蚁群算法需要经过改进后才能应用到移动机器人路径规划中。

1.2 遗传算法

遗传算法（Genetic Algorithm，GA）［4-5］是基于进化论遗传学机理上产生的搜索优化方法。遗传算法具有良好的并行性和较强的通用性，并且该算法具有良好的全局优化和稳定性，操作简单，但是当求解到一定范围时也容易陷入局部最优解。

2 蚁群和遗传算法的改进与融合

蚁群算法［6］和遗传算法［7］是目前应用比较广泛的两种智能仿生算法，已经被应用到科研工程等相关领域。蚁群算法的正反馈机制使其具有更好的全局优化能力以及分布并行计算能力，但在搜索初期由于信息素的匮乏，导致求解效率较低。遗传算法在搜索初期速度快，又适合大范围的搜索，但搜索后期由于无法充分利用系统中的反馈信息，会在冗余迭代上耗费大量的时间。为了克服两种智能算法存在的缺陷，可以对蚁群和遗传算法进有效的融合。

2.1 融合的策略

通过大量的分析研究与实验论证，发现蚁群和遗传两种算法在求解速度与时间上的总体态势如图 1 所示［7-8］。

图1 蚁群算法与遗传算法的速度-时间曲线

由图1可以看出，遗传算法在搜索初期t0～tc时间段，求解速度较快，经过tc时刻后，遗传算法效率开始急速下滑；蚁群算法搜索初期由于信息素信息缺乏，在 t0～tc时刻，效率较低，过了 tc时刻后，蚁群算法效率开始快速上升，最后达到一个较高的稳定状态。

融合算法的思路是在融合算法前期，用遗传算法产生的最优解来初始化蚁群算法的信息素。融合算法后期利用蚁群算法的收敛速度快来寻找最优路径。在遗传算法阶段，统计迭代过程中子代种群的进化率，如果连续n代的进化率都小于预先设定的迭代次数的最小进化率，则遗传算法终止，蚁群算法执行。

2.2 蚁群算法的改进

在蚁群算法中，路径上的信息素的值会随着时间的流逝而减小，在本文中用Rij来进行表示，通过一个递减的指数函数来表示。

式中，tij是蚂蚁从节点i到节点j所花费的时间，是一个常数，Rij的值越大，代表着蚂蚁从节点i到节点j的路径越好。

在每次迭代过程中，只有在指定时间内，最优的蚂蚁才会更新此路径上信息素的值。在式（4）中是最优的蚂蚁经过该路径后此路径上信息素的改变量。Lk第k只蚂蚁走过的路径，是第k只蚂蚁从i节点到k节点花费的时间，是第k只蚂蚁从i节点到k节点学习到的信息。

3 融合算法在移动机器人路径规划中的应用

本文提出融合蚁群和遗传算法（Fusing of Ant Colony and Genetic Algorithm，FACGA），并把该算法应用到移动机器人路径规划中，应用的流程如下页图2。在融合算法中设置遗传算法的最小迭代次数为Gmin，最大迭代次数为Gmax，最小进化率为Gratio，当给定迭代次数范围内连续Gend代的进化率低于Gratio，则终止遗传算法搜索，用遗传算法得到的信息来初始蚁群算法中信息素的初始值，转入蚁群算法求解。算法的步骤如下。

步骤1：初始化交叉概率pc，变异概率pm，以及最大进化代数Gmax，最小进化代数Gmin，最小进化率Gratio，进化结束代数 Gend。

步骤2：设置种群规模为S得初始群体G，使Gmin＜G＜Gmax，根据实际问题进行编码，确定适应度函数，计算种群中个体的适应度值。

步骤3：对种群个体进行解码，执行选择、交叉、变异操作。

步骤4：比较新个体与原父代种群中的个体，根据结果进行个体的优劣替换，选择优良个体作为下一代新的子个体。

步骤 5：若 Gmin＜G＜Gmax且 Gend的进化率 ＞Gratio，则转向步骤3，否则转向步骤6。

步骤6：用遗传算法生成的较优解初始化蚁群算法信息素的初始值。

步骤7：设置蚁群算法最大循环次数为Nmax，蚂蚁个数为m，循环次数k为0。

步骤8：每只蚂蚁根据状态移动规则式（1）选择下一个节点。

步骤9：当蚂蚁k到达终点End时，按式（2）～式（4）对其经过路段上的信息浓度进行更新。

步骤10：重复步骤8、步骤9，直至所有蚂蚁都到达终点End。

步骤11：更新本次迭代最差路径长度及其所包含路段信息，全局最优路径长度及其包含路段信息。

步骤12：把m只蚂蚁的位置重置为起点Start，置空禁忌表。

步骤13：若循环次数k＞Nmax则程序结束，否则转到步骤8。

4 仿真实验

用VC++6.0和MATLAB构建仿真平台，在栅格环境下建模对蚁群算法（ACA）、遗传算法（GA）和本文提出的算法（FACGA）进行分析，设置仿真环境如图3，设定障碍物分布在全局静态10×10的栅格矩阵中，蚂蚁起点为图3中Start，终点为End，蚁群算法中参数为：蚂蚁数量m=20，信息启发算子α和期望启发算子β分别为1和5；信息挥发系数ρ=0.6，遗传算法中参数为：初始种群G为60，运行遗传算法Gmax为60次，每次产生260代，变异概率pm为0.07，交叉概率pc为0.8，图3中障碍物为黑色填充单元格。

仿真结果表明在相同的环境下，在搜索初始阶段，由于基本蚁群算法（ACA）搜索的盲目性，增加了不必要的搜索范围，降低了搜索效率，并且难以搜寻到最优路径；而遗传算法（GA）搜索后期由于无法充分利用系统中的反馈信息，在冗余迭代上需要耗费大量的时间，并且陷入了局部最优。融合蚁群和遗传算法（FACGA）在搜索前期通过把遗传算法的最优解引入到蚁群算法的初始化信息素中，缩小了算法的查询范围，搜索后期又切换到蚁群算法，从而避免了算法陷入局部最优，缩短了寻找最优路径的时间，获得了从Start到End的全局最优路径。验证了本文所提算法的随机性、有效性和全局收敛性。

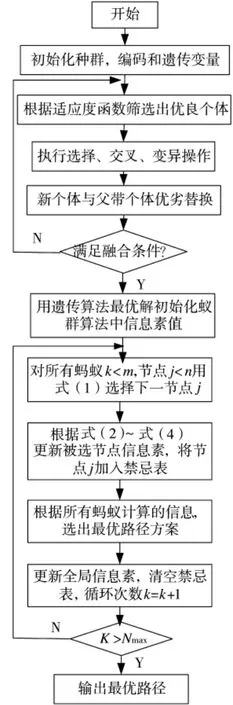
图2 蚁群遗传融合算法路径规划流程图

图3 3种算法路径规划图对比

图4 3种算法路径长度迭代次数对比图

图4中当采用ACA算法进行路径规划时算法收敛需迭代39次，最优路径长度为17.914，当采用GA算法进行路径规划时算法收敛需迭代45次，最优路径长度为17.438，当采用FACGA算法进行路径规划时算法收敛需迭代22次，最优路径长度为16.352，可以看出本文所设计算法FACGA收敛速度更快，收敛路径更短，效率更高。

5 结论

本文通针对蚁群算法和遗传算法在移动机器人路径规划中存在的搜索盲目性大、效率低以及容易陷入局部最优等缺陷，改进了蚁群算法中信息素更新的方法，并且提出了一种基于改进蚁群和遗传算法的融合方案（FACGA），该方案使蚁群和遗传算法优势互补。实验结果表明，本文所提出的方案能提高移动机器人搜索效率，快速找到从起点到终点的较优路径。

［1］赵开新，魏勇.改进蚁群算法在DSR路由协议中的应用［J］.火力与指挥控制，2015，40（7）:135-138.

［2］胡飞虎，田朝晖.基于遗传算法的应急物资分层联动调度研究［J］.计算机应用研究，2016，33（11）:439-443.

［3］赵开新，魏勇.改进蚁群算法在P2P网络资源搜索中的应用［J］.火力与指挥控制，2015，40（5）:139-142.

［4］韩建妙，刘业政.基于遗传算法的超市最短导购路径推荐［J］.计算机工程与应用，2016，52（4）:238-242.

［5］石悦，邱雪松.基于改进遗传算法的电力光传输网规划方法［J］.通信学报，2016，37（1）:116～122.

［6］罗建，薛锋.旅客列车线路选择的蚁群算法求解［J］.计算机工程与应用，2013，49（11）:11-15.

［7］李琳.基于免疫遗传算法的移动机器人轨迹跟踪［J］.华南理工大学学报，2013，47（7）:13-18.

［8］黄永青，杨善林.交互式蚁群遗传算法［J］.小型微型计算机系统，2016，37（11）：2567-2570.