SOME PROPERTIES IN THE GENERALIZED MORREY SPACES ON HOMOGENOUS CARNOT GROUPS

LONG Pin-hong,HAN Hui-li

(School of Mathematics and Computer Science,Ningxia University,Yinchuan 750021,China)

1 Introduction

In the paper,we are mainly concerned with some properties in the generalized Morrey spaces on homogenous Carnot group.As is now well known to all,Morrey space is the classical generalization for Lebesgue space in function space theories.Since the classical Morrey spaces were introduced by Morrey in[26](or refer to[40]),there were many variants and a great deal of progress in the aspect.The classical Morrey spaces together with the weighted Lebesgue spaces,were applied to deal with the local regularity properties of solutions of partial differential equations(refer to[22]).In the local Morrey(or Morrey type)spaces and the global Morrey(or Morrey type)spaces the boundednesses of various classical operators were largely considered,for example,maximal,potential,singular,Hardy operators and commutators and others,here we may refer to Adams[1],Akbulut et al.[2],Adams and Xiao[3–6],Burenkov et al.[9,11],Guliyev et al.[12,15],Chiarenza and Frasca[13],Kurata et al.[23],Komori and Shirai[24],Lukkassen et al.[25],Nakai et al.[27,28],Persson et al.[30],Softova[35],Sugano and Tanaka[36]and references therein.In the classical harmonic analysis,the vanishing Morrey space was firstly introduced by Vitanza[38]to discuss the regularity results for elliptic partial differential equations,and later Ragusa[31]and Samko et al.(see[32,34]and references therein)together systematically studied the boundedness of various classical operators in such these type of spaces.For the characterizations for classical operator in the abstract harmonic analysis,we may refer to some books by Folland and Stein[14],Varopoulos et al.[39]and Thangavelu[37].Guliyev et al.(see[17,18])studied Riesz potential and fractional maximal operator in the generalized Morrey spaces on the Heisenberg group.As for the properties of Lebesgue space on Carnot group in abstract potential theory,we may refer to Bonfiglioli et al.(see[7,8]),Gafofalo and Rotz[19]and Han Yazhou et al.[21].In fact,we know little about the properties of the generalized Morrey space on Carnot group(see only[16]and[29]).Stimulated by the above statements,we continue to study the boundedness of some operators from Samko(see[32–34])in the generalized Morrey spaces on Carnot group and simultaneously develop the results from Bonfiglioli et al.(see[8])on Carnot group.To be exact,our aim is to character the boundedness of the weighted Hardy operator,fractional maximal operator and fractional potential operator in the vanishing generalized Morrey spaces on Carnot group,and simultaneously consider the Morrey-Sobolev type embedding theorems in the generalized Morrey spaces on Carnot group.To establish our results on Carnot group,at first we will recall some notations,classical operators and basic properties on Carnot group below.

A Carnot group is a simply connected nilpotent Lie group G≡(RN,◦)whose Lie algebraGadmits a stratification.That is to say,there exist linear subspacesV1,···,VkofGso that the direct sum vector space decomposition below

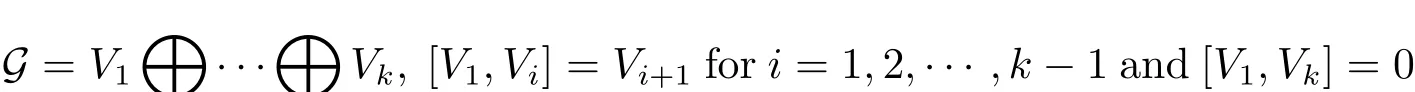
holds,where[V1,Vi]is the subspace ofGgenerated by the elements[X,Y]withX∈V1andY∈Vi.

The dilationsδλ:RN→RN(λ＞0)is a family of automorphisms of group G satisfying

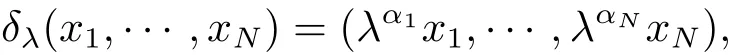
here 1=α1=···=αm＜αm+1≤···≤αNare integers andm=dim(V1).

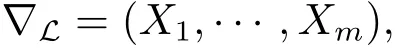
where{X1,···,Xm}is a family of vector fields to form a linear basis of the first layer ofG.

The curveγ:[a,b]→G is called horizontal ifγ(a)=x,γ(b)=y∈G andγ′(t)∈V1for allt.De fine the Carnot-Caratheodory distance betweenxandyby

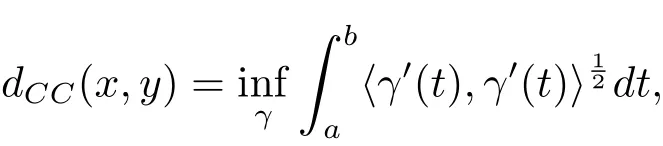
where the infimum is taken over all horizontal curvesγconnecting toxandy.Accordingly,the Carnot-Caratheodory ball is denoted byBCC(x,r)={y∈G:dCC(x,y)＜r}.By the left invariant properties,we see that

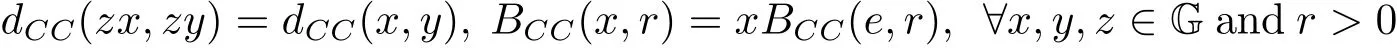
and

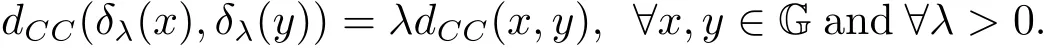
Forx∈G andr＞0,we denote byB(x,r)={y∈G:ρ(y−1◦x)=|y−1◦x|＜r}the G-ball withxand radiusr,and byB(e,r)={y∈G:ρ(y)＜r}the open ball centered at the identity elementeof G with radiusr.Here the continuous functionρ:G→[0,∞)is a homogenous norm on G and satisfiesρ(x−1)=ρ(x),ρ(δtx)=tρ(x)for allx∈G.Moreover,there exists a constantc≥1 such thatρ(xy)≤c(ρ(x)+ρ(y))for allx,y∈G.We remark that the pseudometricρ(x,y)=|x−1◦y|is equivalent to the metricdCCin the following sense

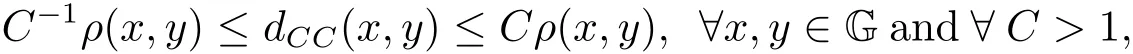
and satisfies

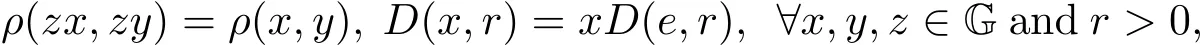
whereD(x,r)={y∈G:ρ(x,y)＜r}is the metric ball associated withρ.For convenience,we will usedandB(x,r)instead ofdCCandBCC(x,r),respectively.

According to the left translation and dilation,it is clearly to know that

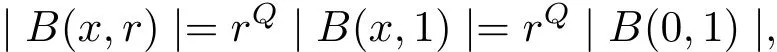
where the homogeneous dimensionQof G is equivalent to

The classical generalized Morrey type spaceLp,ϕ(G)on G is defined by the following norm

for 0≤λ ≤Qand 1≤p≤∞.Hereϕ(x,r)belongs to the class=(G×(0,∞))of non-negative measurable functions on G×[0,∞),which are positive on G×(0,∞).Ifϕ(x,r)=rλ,thenLp,ϕ(G)is exactly the classical Morrey spaceLp,λ(G)for 0≤λ≤Q.Forλ=0 andλ=Q,we know thatLp,0(G)=Lp(G)andLp,Q(G)=L∞(G),respectively.As forλ＜0 andλ＞Q,we knowLp,λ(G)= Θ,where Θ is the set of all functions equivalent to 0 on G.Note that this definition of generalized Morrey type spaceLp,ϕ(G)is slightly different from the Guliyev’s one(refer to[16–18]).

Denote byWLp,ϕ(G)the generalized weak Morrey space of all functionsf∈via

whereWLp(B(x,r))is the weakLp-space of measurable functionsfonB(x,r)with the norm

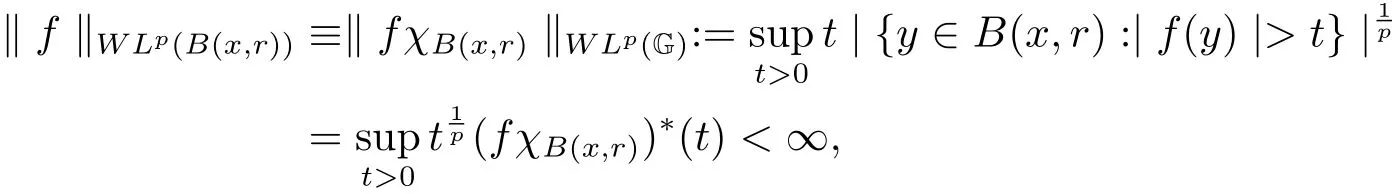
whereg∗denotes the non-increasing rearrangement of the functiong.

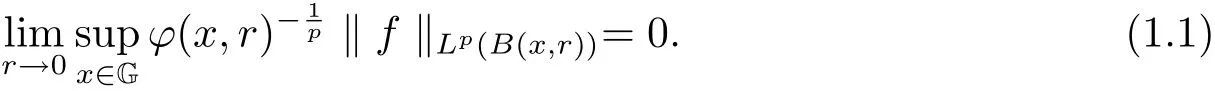
The vanishing generalized Morrey spaceV Lp,ϕ(G)is defined as the spaces of all functionsf∈Lp,ϕ(G)such that Correspondingly,the vanishing generalized weak Morrey spaceV WLp,ϕ(G)is defined as the spaces of all functionsf∈WLp,ϕ(G)such that

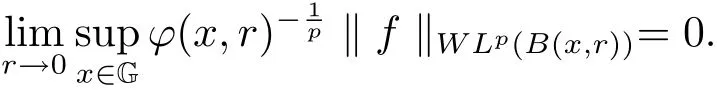
Obviously,it is natural to impose onϕ(x,r)with the following conditions

and

From conditions(1.2)and(1.3),we easily know that the bounded functions with compact support belong toV Lp,ϕ(G)andV WLp,ϕ(G).

In the paper,we firstly consider the multi-dimensional weighted Hardy operators as follows

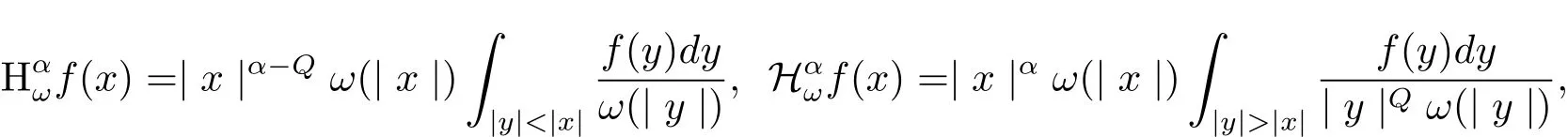
whereα≥0.In the sequel G withQ=1,the Hardy operators above may be read with the versions Ifω(t)=tβ,then the operators above are denoted by

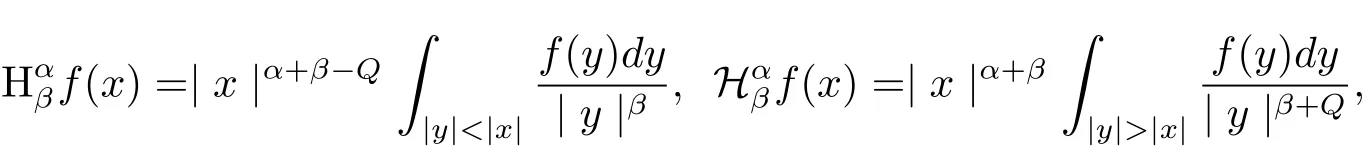
and the one-dimensional by

Besides,we also consider some operators as follows.

(1)Forf∈the fractional maximal operatorMαfwith orderαof the functionfis defined by

where the supremum is taken over all the ballsB(·,r)in G.Whenα=0,Mαis the centered Hardy-Littlewood maximal operatorM.

(2)The potential type operator with orderαis denoted by

hereI(·,y)=d(·,y)α−Q.Here we also callIαfthe G-fractional integral with orderαoff.

Letfbe a non-negative function on[0,ℓ].If there exists a constantC≥1 such thatf(x)≤Cf(y)for allx≤yorx≥y,thenfis named almost increasing or decreasing.Moreover,if the two almost increasing or decreasing functionsfandgsatisfyc1f≤g≤c2fforc1,c2＞0,then they are equivalent.

Definition 1.1 Let 0＜ℓ≤∞.

Denote byW=W([0,ℓ])the class of continuous and positive functionsφ(r)on(0,ℓ]such that the limitexists and is finite.

Denote byW0=W0([0,ℓ])the class of almost increasing functionsφ(r)∈Won(0,ℓ).

In the rest of this paper,we will make some arrangement as follows.In Section 2,we will introduce some necessary lemmas.In Section 3,we will discuss our main theorems and their proofs.

2 Some Necessary Lemmas

In the section,we have something in mind to list the related lemmas.At first we provide two results with similar ones from Persson and Samko(see[30,Proposition 3.6,3.8])as well as Euclidean setting.

Lemma 2.1 For 1≤p＜∞,0＜s≤pand 1≤ℓ≤∞,letν(t)∈ν(2t)≤Cν(t)([0,ℓ])forx∈G.Then

whereC＞0 does not depend onyandf,and

Lemma 2.2 For 1≤p＜∞and 0≤s≤p,letϕ(r)≥CrQandν(t)∈W(R+).Then

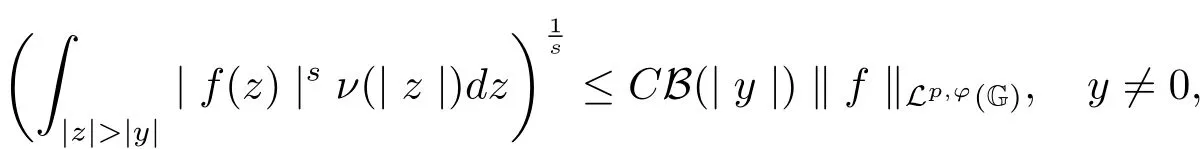
whereC＞0 does not depend onyandf,and

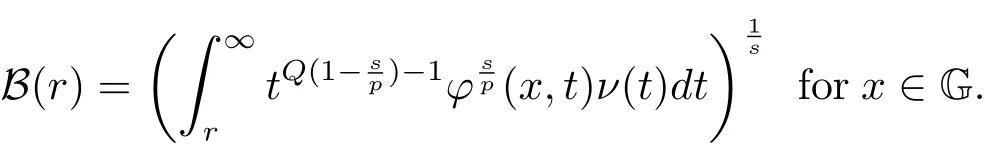
Next we will introduce the Hardy-Littlewood-Sobolev theorem for subLaplacians,which was proved by Bonfiglioli et al.in[8].

Lemma 2.3(see[8],Theorem 5.9.1)LetLbe a subLaplacian on the homogeneous Carnot group G anddbe anL-gauge.Suppose 0＜α＜Q,1＜pThen there exists a positive constantC=C(α,p,G,d,L)such that

here the notation‖·‖Lrdenotes theLrnorm in G=RNwith respect to the Lebesghe measure.

3 Statements of Main Results

In the section we start to sate our main theorems.Firstly we consider the boundedness of weighted Hardy operator in the vanishing Morrey type space.

Theorem 3.1 Let 1≤p,q＜∞andϕsatisfy conditions(1.1)–(1.3).

(I)Suppose thatω ∈W([0,ℓ]),ω(2t)≤Cω(t),

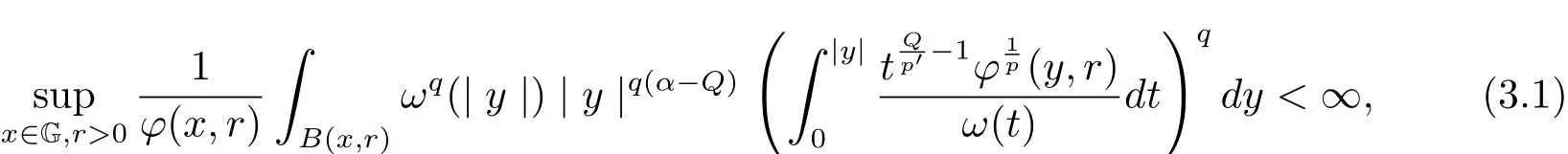
(II)Suppose thatω∈andω(2t)≤Cω(t)or

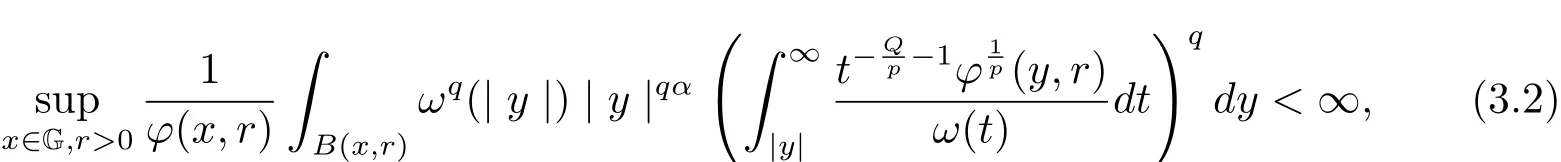
Proof Puts=1 andν(t)=ω(t)in Lemma 2.1.Then

fory∈B(x,r),and we obtain

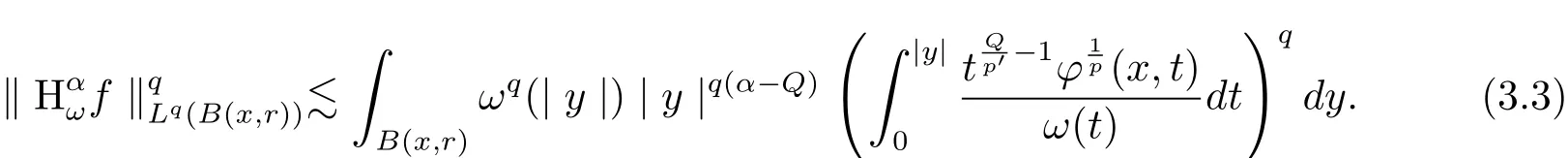
That is to say

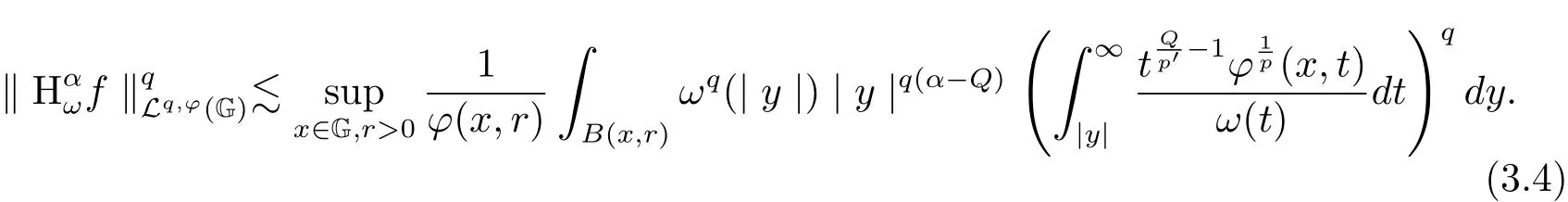
On the other hand,by inequality(3.3)and conditions(1.1)–(1.2),we get that

Similarly,applying Lemma 2.2 intowe have

fory∈B(x,r),and we know that

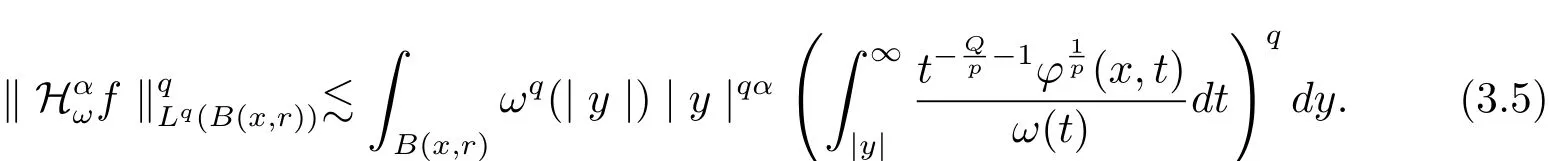
Therefore

Second,we will deal with the boundedness of fractional maximal operator and potential operator in the vanishing generalized Morrey space.Whenϕ(x,r)=rλandψ(x,r)=rµ,we may obtain Corollary 3.1.

Theorem 3.2 LetLbe a subLaplacian on the homogeneous Carnot group G anddbe anL-gauge.Suppose 0＜α＜Q,1＜pandϕ,ψ∈.If

for everyδ＞0 and

whereC0doesn’t depend onx∈G andr＞0,then there exists a positive constantC=C(α,p,G,d,L)such that‖‖Lq,ψ(G)≤C‖f‖Lp,ϕ(G),‖Iαf‖Lq,ψ(G)≤C‖f‖Lp,ϕ(G).Moreover,ifϕandψalso satisfy conditions(1.1)–(1.3),then the operatorsandIαare bounded fromV Lp,ϕ(G)toV Lq,ψ(G).

Here we firstly recall the definition ofL-gauged.Ifdis a homogeneous symmetric norm being smooth out of the origin and satisfyingL(d2−Q)=0 in G{0},then we calld L-gauge on G(see Section 5.4 in[8]).

Proof As is well known,Mαf≤CIα(|f|),and we only consider the case forIα.At first we divide the functionfinto the expressionf=f1+f2so thatIαf=Iαf1+Iαf2,wheref1=fχB(x,2r)andf2=fχGB(x,2r).From Lemma 2.3,we see that

Then

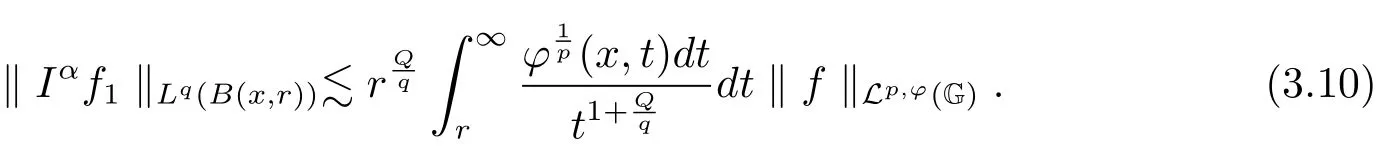
Since there exist two constantsc1,c2≥1 so that the inequality≤d(x,y)≤c2d(y,z)holds forz∈B(x,r)andy∈GB(x,2r),and therefore

Putγ＞Since‖χB(x,R)‖Lp(G)～,by the H¨older inequality and Fubini’s theorem,it follows that

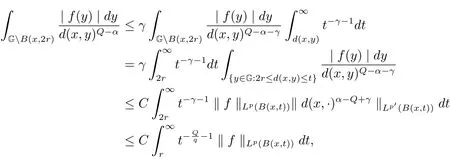
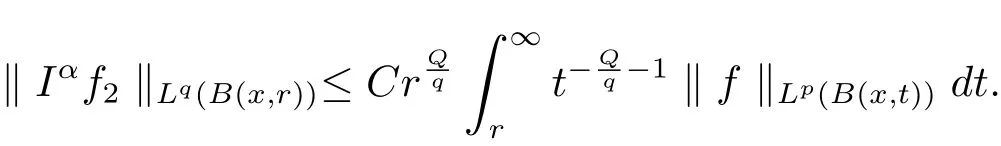
Hence

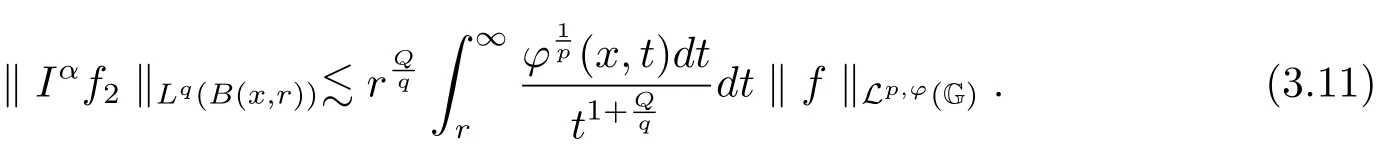
From inequalities(3.10)and(3.11),we see that

By inequalities(3.7)–(3.8)and conditions(1.1)–(1.3),it follows that‖Iαf‖Lq,ψ(G)≤C‖f‖Lp,ϕ(G),and the potential operatorIαis bounded in the vanishing generalized Morrey spaceV Lp,ϕ(G)to another vanishing generalized Morrey spaceV Lp,ψ(G).

Corollary 3.1 LetLbe a subLaplacian on the homogeneous Carnot group G anddbe anL-gauge.Suppose 0＜α＜Q,1＜pand 0＜λ＜Q−αp.then the operatorsare bounded fromV Lp,λ(G)toV Lq,µ(G),where

In Section 5.3 in[8],the function Γ is defined as the fundamental solution for subLaplacianLon homogeneous Carnot group.That is to say,−L(Γ(y−1◦·))=Diracyholds in the weak sense of distribution,where Diracyis the dirac measure supported aty.Now we intend to study the Sobolev-Stein embedding theorem and accordingly give the the Morrey-Sobolev-Stein embedding theorem in generalized Morrey space on homogenous Carnot group.

Theorem 3.3 LetLbe a subLaplacian on the homogeneous Carnot group G of homogenous dimensionQanddbe anL-gauge.Suppose 0＜α＜Qandϕ,ψ∈.If

for everyδ＞0 and

whereC0doesn’t depend onx∈G andr＞0,then there exists a positive constantC=C(α,p,G,d,L)such that

Proof Applying the representation formula of solution of Dirichlet problem for sub-Laplacian tou∈(G,R),by integrating by parts,we see that

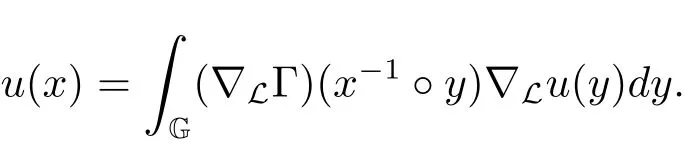
Since∇Lis smooth in G{0}andδ-homogeneous of degree zero,there exists a suitable constantCdepending only onLso that

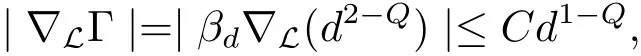
whereβdis a constant depended ond.Consequently,

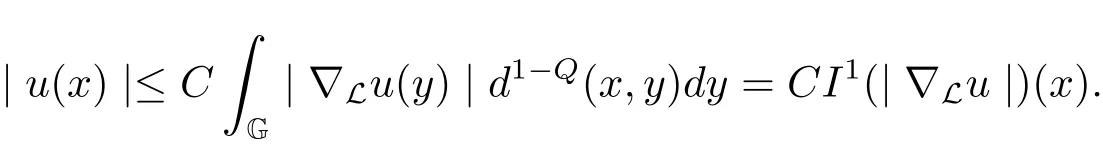
Therefore,from Theorem 3.2,we obtain that

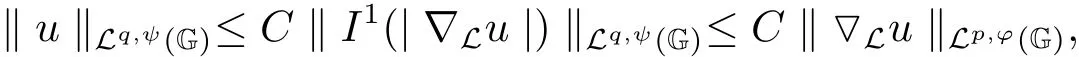
which is exactly the desired results to prove.Setϕ(x,r)=rλandψ(x,r)=rµin Theorem 3.3.It is known that(G,R)is sense in(G,R)but notLp,λ(G,R).Hence by Theorem 3.3,we may easily infer the next corollary.

Corollary 3.2 LetLbe a subLaplacian on the homogeneous Carnot group G anddbe anL-gauge.Suppose 0＜α,λ＜Qand 1＜pThen there exists a positive constantC=C(α,p,G,d,L)such that

where

[1]Adams D R.A note on Riesz potentials[J].Duke Math.J.,1975,42(4):765–778.

[2]Akbulut A,Guliyev V S,Mustafayev R Ch.On the boundedness of the maximal operators and singular integral operators in generalized Morrey spaces[J].Math.Bohem.,2012,137(1):27–43.

[3]Adams D R,Xiao J.Nonlinear potential analysis on Morrey spaces and their capacities[J].Indiana Univ.Math.J.,2004,53(6):1629–1663.

[4]Adams D R,Xiao J.Morrey potentials and harmonic maps[J].Comm.Math.Phys.,2011,308:439–456.

[5]Adams D R,Xiao J.Regularity of Morrey commutators[J].Trans.Amer.Math.Soc.,2012,364:4801–4818.

[6]Adams D R,Xiao J.Morrey spaces in harmonic analysis[J].Ark.Mat.,2012,50:201–230.

[7]Bonfiglioli A,Lanconelli E.Subharmonic functions on Carnot groups[J].Math.Ann.,2003,325:97–122.

[8]Bonfiglioli A,Lanconelli E,Uguzzoni F.Strati field Lie groups and potential theory for their sub-Laplacian[M].Berlin,Heidelberg:Springer-Verlag,2007.

[9]Burenkov V I,Guliyev V S.Necessary and suきcient conditions for the boundedness of the Riesz potential in local Morrey type spaces[J].Potential Anal.,2009,30(3):211–249.

[10]Burenkov V,Gogatishvili A,Guliyev V S,Mustafayev R Ch.Boundedness of the fractional maximal operator in local Morrey type spaces[J].Compl.Var.Ell.Equ.,2010,55(8-10):739–758.

[11]Burenkov V,Gogatishvili A,Guliyev V S,Mustafayev R Ch.Boundedness of the fractional maximal operator in local Morrey type spaces[J].Potential Anal.,2011,35(1):67–87.

[12]Burenkov V I,Guliyev V S,Serbetci A,Tararykova T V.Necessary and suきcient conditions for the boundedness of genuine singular integral operators in local Morrey type spaces[J].Eurasian Math.J.,2010,1:32–53.

[13]Chiarenza F,Frasca M.Morrey spaces and Hardy-Littlewood maximal function[J].Rend.Math.,1987,7(7):273–279.

[14]Folland G B,Stein E M.Hardy spaces on homogeneous groups,mathematical notes,28[M].New York:Princeton University Press,1982.

[15]Guliyev V S,Aliyev S S,Karaman T,Shukurov P S.Boundedness of sublinear operators and commutators on generalized Morrey spaces[J].Integ.Equ.Oper.The.,2011,71(3):327–355.

[16]Guliyev V S,Akbulut A,Mammadov Y Y.Boundedness of fractional maximal operators and their higher order commutators in generalized Morrey spaces on Carnot groups[J].Acta Math.Sci.,2013,33B(5):1329–1346.

[17]Guliyev V S,Eroglu A,Mammadov Y Y.Riesz potential in generalized Morrey spaces on the Heisenberg group[J].J.Math.Sci.,2013,189(3):365–382.

[18]Guliyev V S,Mammadov Y Y.Boundedness of fractional maximal operators in generalized Morrey spaces on the Heisenberg group[J].Indian J.Pure Appl.Math.,2013,44(2):185–202.

[19]Garofalo N,Rotz K.Properties of a frequency of Almgren type for harmonic functions in Carnot groups[J].Calc.Var.,2015,54:2197–2238.

[20]Heinonen J,Kilpel¨ainen T,Martio O.Nonlinear potential theory of degenerate elliptic equations,Oxford mathematical monographs[M].Oxford:Oxford University Press,1993.

[21]Han Yazhou,Luo Xuebo,Niu Pengcheng.A Liouville type theorem of semilinear equations on the Carnot group[J].J.of Math.(PRC),2007,27(6):149–153.

[22]Kufner A O,John O,Fucik S.Function spaces[M].Leyden:NoordhoffInternational Publishing,Prague:Publishing House Czechoslovak Academy of Sciences,1977.

[23]Kurata K,Nishigaki S,Sugano S.Boundedness of integral operators on generalized Morrey spaces and its application to Schr¯odinger operators[J].Proc.Am.Math.Soc.,2000,128(4):1125–1134.

[24]Komori Y,Shirai S.Weighted Morrey spaces and a singular integral operator[J].Math.Nachr.,2009,282(2):219–231.

[25]Lukkassen D,Meidell A,Persson L E,Samko N.Hardy and singular operators in weighted generalized Morrey spaces with applications to singular integral equations[J].Math.Meth.Appl.Sci.,2012,35(11):1300–1311.

[26]Morrey C B.on the solutions of quasi-linear elliptic partial differential equations[J].Trans.Amer.Math.Soc.,1938,43:126–166.

[27]Nakai E.Hardy-Littlewood maximal operator,singular integral operators and the Riesz potentials on generalized Morrey spaces[J].Math.Nachr.,1994,166:95–103.

[28]Nakai E.Generalized fractional integrals on generalized Morrey spaces[J].Math.Nachr.,2014,287(2-3):339–351.

[29]Nakai E.The Campanato,Morrey and H¨older spaces on spaces of homogeneous type[J].Studia Math.,2006,176(1):1-19.

[30]Persson L E,Samko N.Weighted Hardy and potential operators in the generalized Morrey spaces[J].J.Math.Anal.Appl.,2011,377(2):792–806.

[31]Ragusa M A.Commutators of fractional integral operators on Vanishing Morrey spaces[J].J.Glob.Optim.,2008,40(1-3):361–368.

[32]Samko N.Weighted Hardy and singular operators in Morrey spaces[J].J.Math.Anal.Appl.,2009,350(1):56–72.

[33]Samko N.Weighted Hardy operators in the local generalized vanishing Morrey spaces[J].Positivity,2013,17(3):683–706.

[34]Samko N.On Maximal,potential and singular operators in vanishing generalized Morrey spaces[J].J.Glob.Optim.,2013,57(4):1385–1399.

[35]Softova L.Singular integrals and commutators in generalized Morrey spaces[J].Acta Math.Sin.,Engl.Ser.,2006,22(3):757–766.

[36]Sugano S,Tanaka H.Boundedness of fractional integral operators on generalized Morrey spaces[J].Sci.Math.Jpn.,2003,58(3):531–540.

[37]Thangavelu S.Harmonic analysis on the Heisenberg group,vol.159 of progress in mathematics[M].Boston:Birkh¨auser,1998.

[38]Vitanza C.Functions with vanishing Morrey norm and elliptic partial differential equations[A].Proceedings of methods of real analysis and partial differential equations[C].Capri:Springer,1990.

[39]Varopoulos N,Saloff-Coste L,Coulhon T.Analysis and geometry on groups[M].New York:Cambridge Univ Press,1992.

[40]Zorko C T.Morrey space[J].Proc.Amer.Math.Soc.,1986,98(4):586–592.