THE NEHARI MANIFOLD FOR A QUSILINEAR SUB-ELLIPTIC EQUATION WITH A SIGN-CHANGING WEIGHT FUNCTION ON THE HEISENBERG GROUP

CHEN Nan-bo,TU Qiang

(School of Mathematics and Statistics,Wuhan University,Wuhan 430072,China)

1 Introduction

In this paper,we shall discuss the existence and multiplicity of non-negative solutions for the following nonlinear boundary value problem

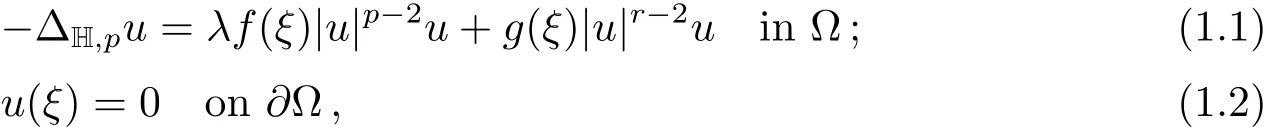
where Ω is a bounded region with smooth boundary in HN,1＜p＜r0 is a real parameter andf,g:Ω→R are given functions which change sign on Ω,i.e.f,gare indefinite weight functions.We assume thatf(ξ),g(ξ)∈L∞(Ω),f(ξ)|u|pdξ＞0}/=Øand{u

Problems(1.1)–(1.2)are studied in connection with the corresponding eigenvalue problem for thep-sub-Laplacian

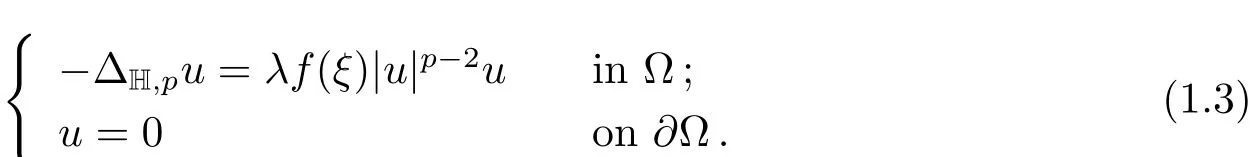
Over the recent past decade,several authors used the Nehari manifold and fibering maps(i.e.,maps of the formt→Jλ(tu),whereJλis the Euler function associated to the equation)to solve semilinear and quasilinear problems(see[3–9,12]).By the fibering method,Drabek and Pohozaev[9],Bozhkov and Mitidieri[12]studied respectively the existence of multiple solutions to the followingp-Laplacian equation

In[6],from the viewpoint of the Nehari manifold,the authors studied the following subcritical semilinear elliptic equation with a sign-changing weight function(

where 2＜rλis constant,andf(x),g(x)are smooth functions which may change sign in Ω.Exploiting the relationship between the Nehari manifold and fibering maps,they gave an interesting explanation of the well-known bifurcation result.In fact,the nature of the Nehari manifold changes as the parameterλcrosses the bifurcation value.In[8],the author dealt with the similar problem for the case 1＜r＜2 and discussed the existence and multiplicity of non-negative solutions of(1.5)from a variational viewpoint making use of the Nehari manifold.

The Dirichlet problems(1.1)–(1.2)on the Heisenberg group is a natural generalization of the classical problem on RN,see[6–11]and their references.It is well known that(1.4)and(1.5)are counterparts of(1.1)–(1.2)in RN.In this work,we use a variational method which is similar to the fibering method(see[9])to prove the existence and multiplicity of positive weak solution for problems(1.1)–(1.2),particularly,by using the method of[6].

This paper,except for the introduction,is divided into four sections.In Section 2,we firstly recall some basic facts and necessary known results on the Heisenberg group,and then we consider the eigenvalue problem(1.3).In Section 3,we focus on the Nehari manifold and the connection between the Nehari manifold and the fibrering maps.In Section 4,we discuss the Nehari manifold whenλ＜λ1(f)and show how the behaviour of the manifold asdepends on the sign ofdξ.In Section 5,using the properties of Nehari manifold we give simple proofs of the existence of two positive solutions.

2 Notations and Preliminaries

Letξ=(x1,···,xN,y1,···,yN,t)=(x,y,t)=(z,t)∈R2N+1withN≥1.The Heisenberg group HNis the set R2N+1equipped with the group law

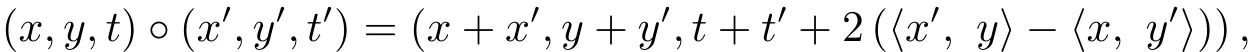
where〈·,·〉denotes the inner product in RN.This group multiplication endows HNwith a structure of a Lie group.A family of dilations on HNis defined asδτ(x,y,t)=(τx,τy,τ2t),τ＞0.The homogeneous dimension with respect to dilations isQ=2N+2.The sub-Laplacian ΔHis obtained from the vector fieldsXi=∂xi+2yi∂t,Yi=∂yi−2xi∂t,i=1,···,N,as

i.e.,

where∇His the 2n-vector(X1,···,XN,Y1,···,YN).

Forp＞1,the sub-p-Laplacian ΔH,pis defined as

For more details concerning the Heisenberg group,see[1,2].

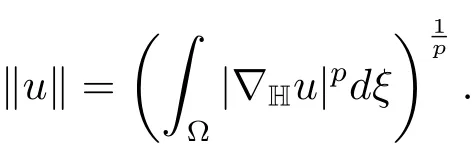
For notational convenience,we denote(Ω)and define the norm inLp(Ω)by‖u‖p.

The following lemma will be referred to as the Folland-Stein embedding theorem.

Lemma 2.1(see[19])Let Ω⊂HNbe a bounded domain.Then the following inclusion is compact

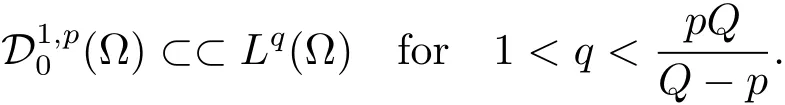
According to the continuity of the Nemytskii operator(see[20,22])and Lemma 2.1,f∈L∞(Ω)implies that

(f)the functional

is weakly continuous onX.

Analogously,it follows fromg∈L∞(Ω)and 1＜r

(g)the functional

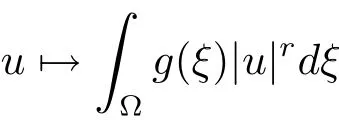
is weakly continuous onX.

Now,we consider the nonlinear eigenvalue problem(1.3).This eigenvalue problem is also of independent interest(see[13–15]).Set

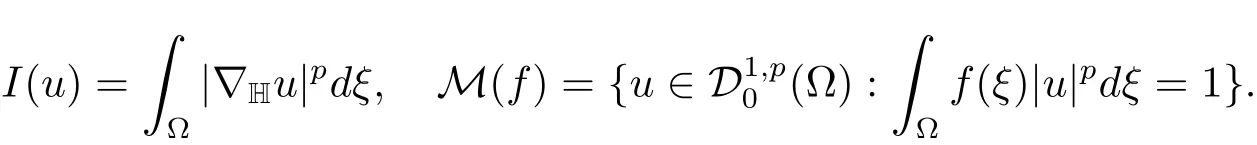
From the definition of the spaceit is obvious thatIis coercive and weakly lower semi-continuous.We have the following theorem.

Theorem 2.1 If 1＜p＜Qandf(ξ)satisfies the conditions above,then

(i)there exists the first positive eigenvalueλ1(f)of(1.3)which is variationally expressed as

(ii)λ1(f)is simple,i.e.,the eigenfunctions associated toλ1(f)are merely a constant multiple of each other;

(iii)λ1(f)is unique,i.e.,ifv≥0 is an eigenfunction associated with an eigenvalueλwiththenλ=λ1(f).

A key point of the proof of Theorem 2.1 lies on the following lemma.

Lemma 2.2(see[16])Letu≥0 andv＞0 be differentiable functions on Ω⊂HN,where Ω is a bounded or unbounded domain in HN.Then we have

where

forp＞1.Moreover,L(u,v)=0 a.e.on Ω if and only ifa.e.on Ω.

A direct consequence of Theorem 2.1 is

Corollary 2.1 If 1＜p＜Q,0＜λ＜λ1(f)andf(ξ)satisfies the conditions above,then the eigenvalue problem

has the first positive eigenvalueµ1(λ)which is variationally expressed as

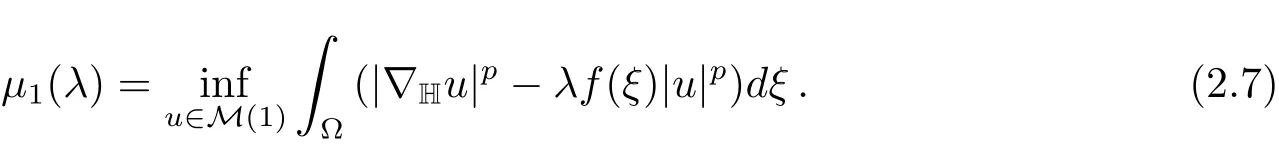
Moreover,µ1(λ)is simple and unique.

3 The Nehari Manifold

The Euler-Lagrange functional associated with(1.1)–(1.2)is

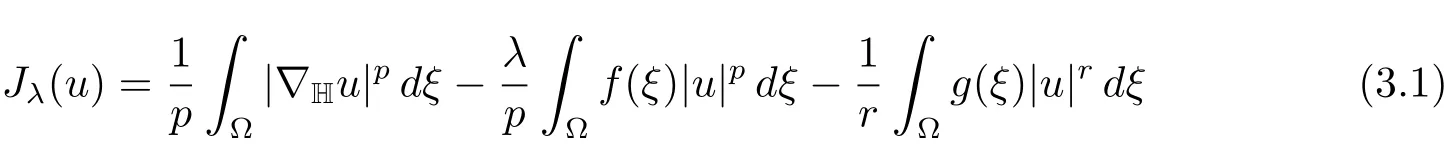
for allu∈X.Jλmay be not bounded from below on wholeX,sincep＜r.In order to obtain existence results in this case,we introduce the Nehari manifold

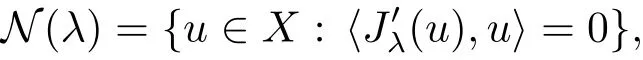
where〈,〉denotes the usual duality betweenXandX∗.Thusu∈N(λ)if and only if

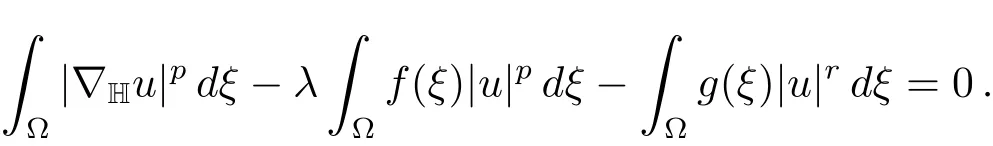
ClearlyN(λ)is a much smaller set thanXand,as we will see below,Jλis much better behaved onN(λ).In particular,onN(λ)we have that

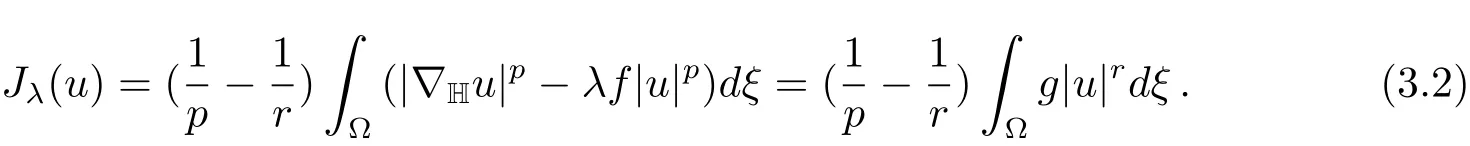
The Nehari manifold is closely linked to the behaviour of the functions of the formφu:t→Jλ(tu)(t＞0).Such maps are known as fibrering maps and were introduced by Drabek and Pohozaev in[9].They were also discussed in[6]and[8].Ifu∈X,we have

It is easy to see thatu∈N(λ)if and only ifMore generally,if and only iftu∈N(λ),i.e.,elements inN(λ)correspond to stationary points of fibering maps.Thus it is natural to subdivideN(λ)into sets corresponding to local minima,local maxima and points of inflection,respectively.It follows from(3.4)and(3.5)that,implies

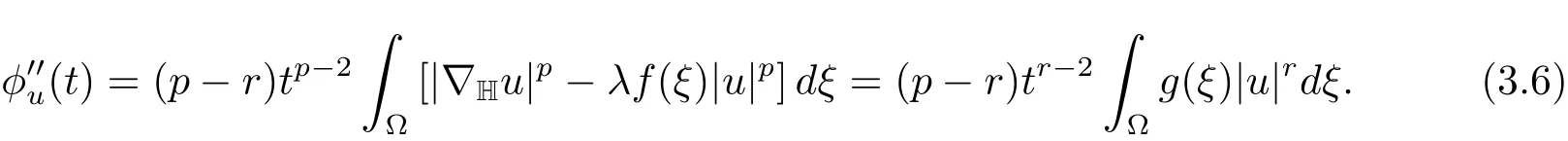
Thus we define

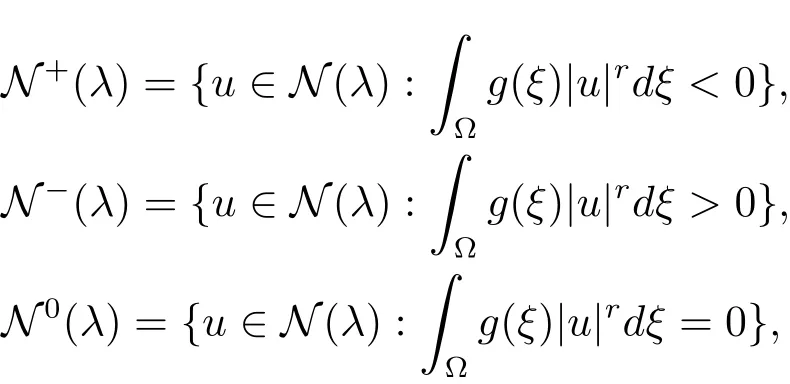
so thatN+(λ),N−(λ),N0(λ)correspond to minima,maxima and points of inflection,respectively.

Letu∈X.Then

(i)ifdξand have the same sign,φuhas exactly one turning point at

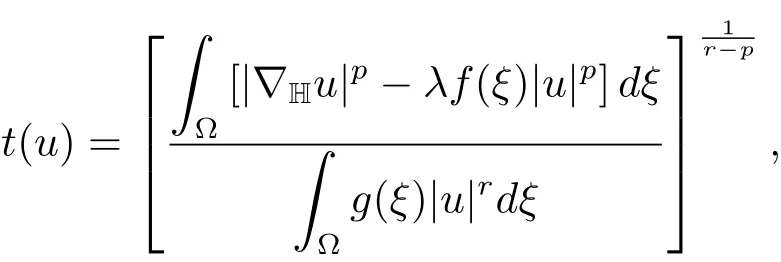
this turning point is a minimum(maximum)so thatt(u)u∈N+(λ)(N−(λ))if and only if

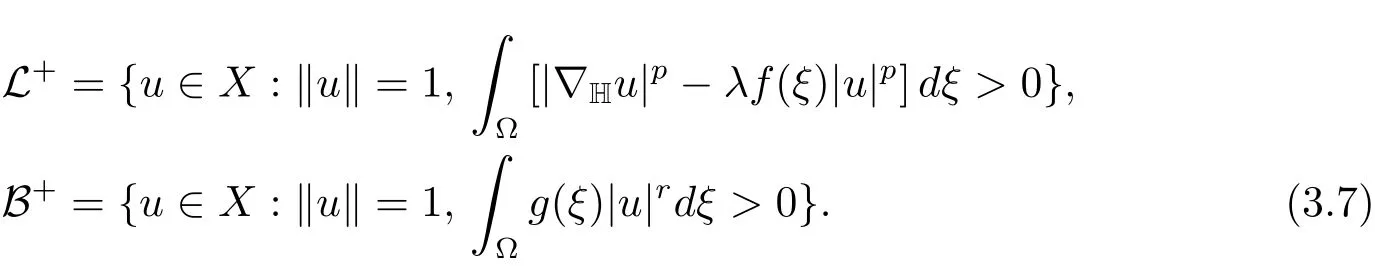
Analogously we can defineL−,L0,B−,B0by replacing ‘＞0’in(3.7)by ‘＜0’or ‘=0’,respectively.Then we have

(i)ifu∈L+∩B+,then the fibering mapφuhas a unique critical point which is a local maximum.Moreover,t(u)u∈N−(λ);

(ii)ifu∈L−∩B−,then the fibering mapφuhas a unique critical point which is a local minimum.Moreover,t(u)u∈N+(λ);

(iii)ifu∈L+∩B−,then the fibering mapφuis strictly increasing and no multiple ofulies inN(λ);

(iv)ifu∈L−∩B+,then the fibering mapφuis strictly decreasing and no multiple ofulies inN(λ).

Thus the following theorem holds.

Theorem 3.1 Ifu∈X{0},then

(a)a multiple ofulies inN−(λ)if and only iflies inL+∩B+;

(b)a multiple ofulies inN+(λ)if and only iflies inL−∩B−;

(c)no multiple ofulies inN(λ)ifu∈L+∩B−oru∈L−∩B+.

The following lemma was stated in[6](see also[17])which showed that minimizers onN(λ)are also critical points forJλonX.

Lemma 3.1 Suppose thatu0is a local maximum or minimum forJλonN(λ).Then ifu0/∈N0(λ),u0is a critical point ofJλ.

4 The Case When λ＜λ1(f)

In this section,we discuss the Nehari manifold whenλ＜λ1(f)and show how the behaviour of the manifold asλ→depends on the sign ofAs a consequence,we obtain that equations(1.1)–(1.2)have at least one positive solution in this case.

Suppose 0＜λ＜λ1(f).It follows from(2.7)that there existsδ(λ)＞0 such that

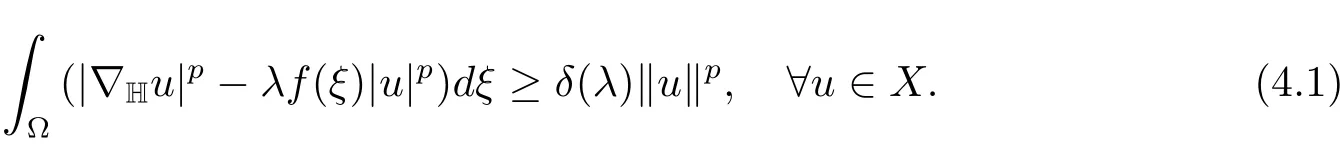
Thus by(4.1),we have

Lemma 4.1 If 1＜λ＜λ1(f),thenL−,L0andN+(λ)are empty andN0(λ)={0}.Moreover,N−(λ)={t(u)u:u∈B+}andN(λ)=N−(λ)∩{0}.

We now investigate the behavior ofJλonN−(λ).In view of the preceding lemma,we have

Theorem 4.1 If 0＜λ＜λ1(f),then

Proof By(3.2)and the structure ofN−(λ),we easily obtainJλ(u)＞0 wheneveru∈N−(λ)and soJλ(u)is bounded from below by 0 onN−(λ).Letu∈N−(λ),thenandu=t(v)vwheret(v)=DenoteandK1/ris a Folland-Stein embedding constant.Thenb∗＞0 and

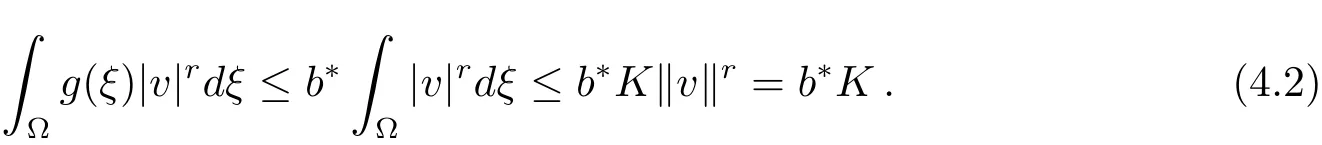
Combining(4.1)and(4.2),it yields that and

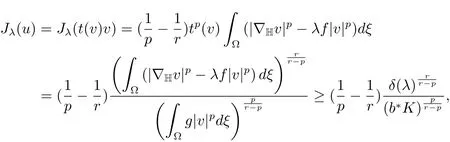
Next,we will show that there exists a minimizer onN−(λ)which is a critical point ofJλand also a nontrivial solution of(1.1)–(1.2).

Theorem 4.2 If 0＜λ＜λ1(f),then there exists a minimizer ofJλonN−(λ)which is a critical point ofJλ.

ProofLet{um}⊂N−(λ)be a minimizing sequence,i.e.,

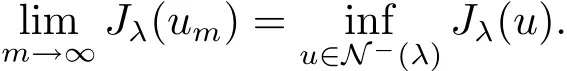
Using(3.2)and(4.1),we obtain

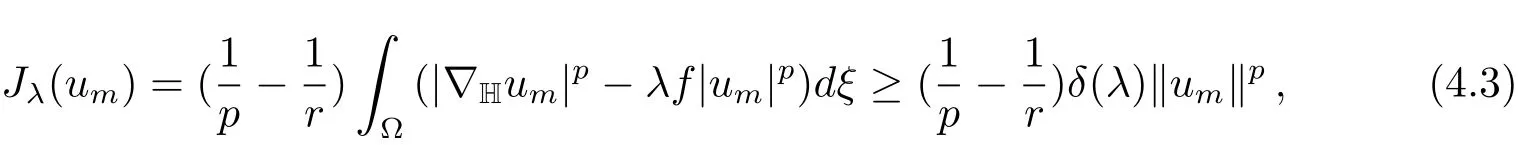
thus the sequence{um}is bounded inX,and so we may assume passing to a subsequence thatum⇀u0inX.Since

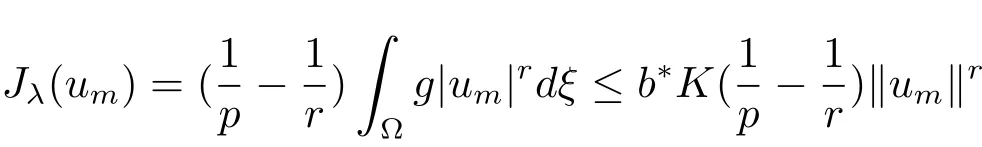
together with(4.3)implies that‖um‖ ≥εfor someε＞0.Using(4.3)again,we deduce that

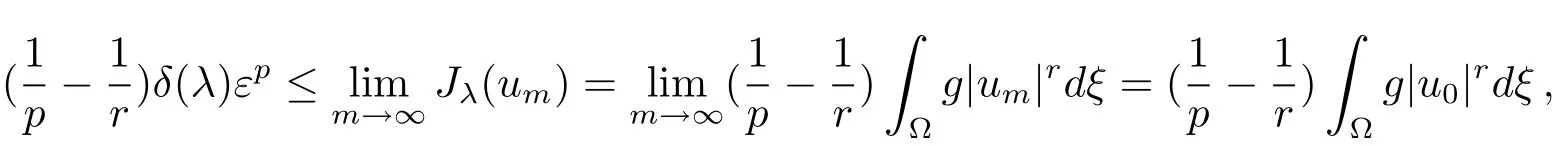
which implies thatu0/=0.By(4.1),we get

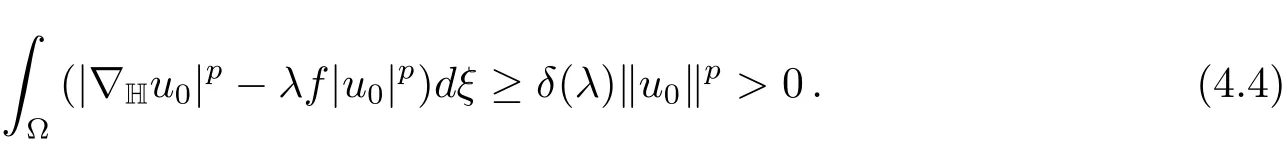
We claim thatum→u0inX.Suppose the contradiction,then we have‖u0‖＜Together with(f)and(g)in Section 2,it yields

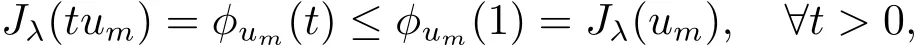
andJλ(αum)≤Jλ(um).Note thatαum⇀αu0and‖u0‖we obtain

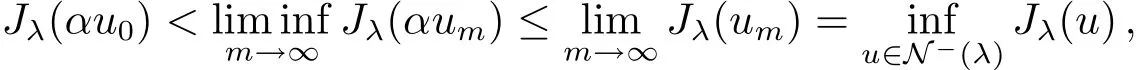
i.e.,it is a contradiction.Thereforeum→u0inX.This implies that

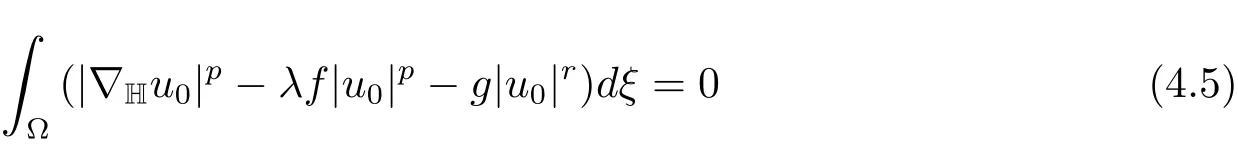
and

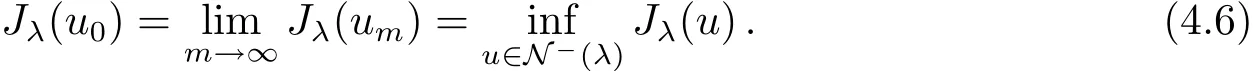
From(4.5),(4.4)and(4.6),we conclude thatu0is a minimizer forJλonN−(λ).Sincedξ＞0,u0∈/N0(λ).By Lemma 3.1u0is a critical point ofJλ.SinceJλ(|u|)=Jλ(u),by applying Harnack inequality[18],we may assume thatu0is positive.

As a direct consequence of Theorem 4.2,we obtain the following existence theorem.

Theorem 4.3 Equations(1.1)–(1.2)have at least one positive solution whenever 0＜λ＜λ1(f).

We conclude this section by proving some properties of the branch of solutions bifurcated fromλ1(f)whenever the conditiondξ＞0 is satisfied.The case wheredξ＜0 which gives rise to multiple solutions whenλ＞λ1(f)will be discussed in the next section.

(ii)ifλm→andumis a minimizer ofJλmonN−(λ)(we may assume thatum＞0),thenMoreover,

Proof(i)We may assume,without loss of generality,that‖φ1‖=1.Sincedξ＞0 andλ＜λ1(f),we haveφ1∈L+∩B+.Hencet(φ1)φ1∈N−(λ),where

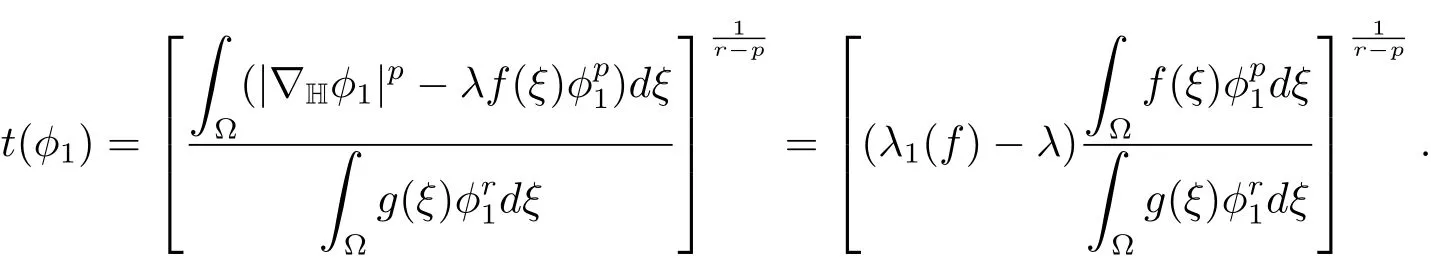
Therefore we have

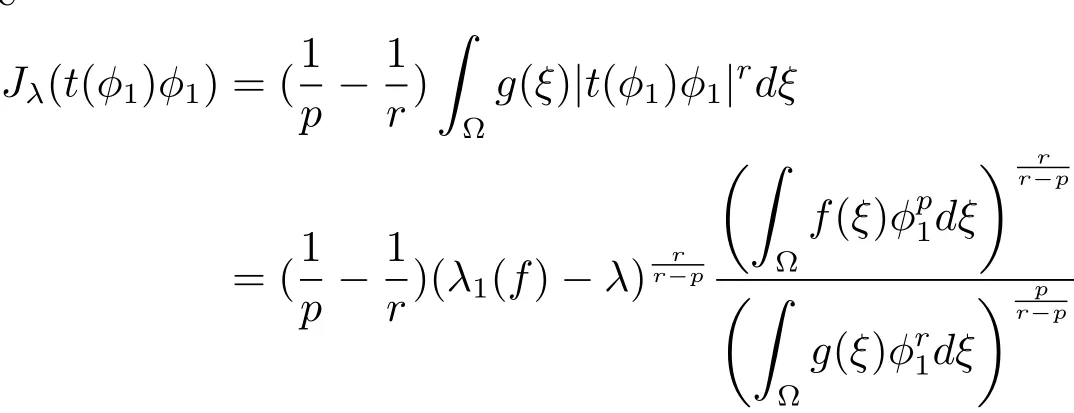
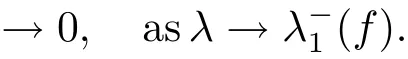
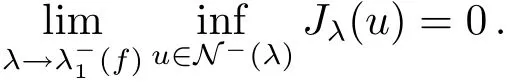
(ii)First,we show that every minimizing sequence{um}onN−(λ)is bounded.Suppose otherwise,then we may assume without loss of generality that‖um‖→∞.we may assume thatvm⇀v0inX.By(f)and(g),we have

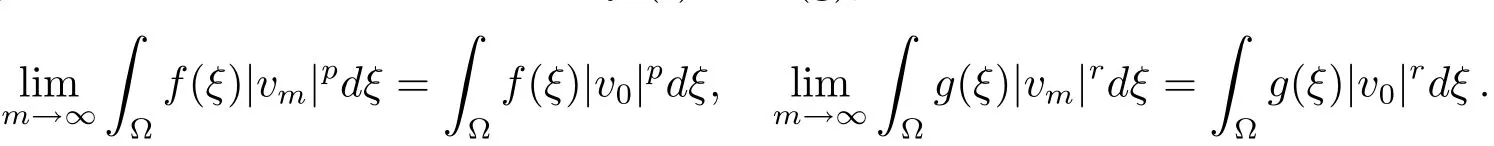
Using(i),we obtain

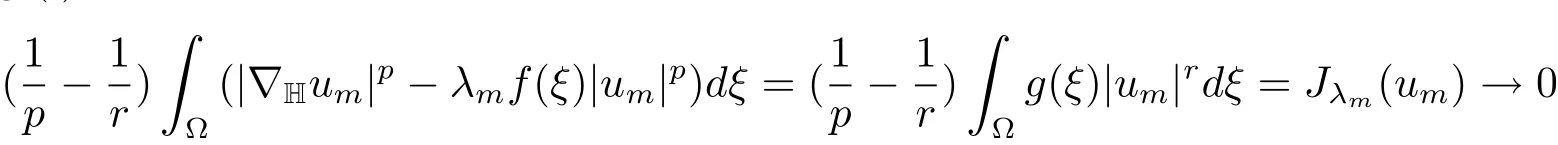
asm→∞.Divided by‖um‖p,we have

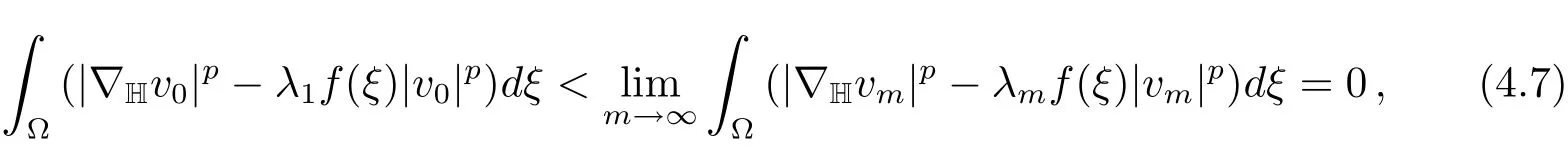
which is a contradiction for(2.4).Hencevm→v0inX.Thus we have

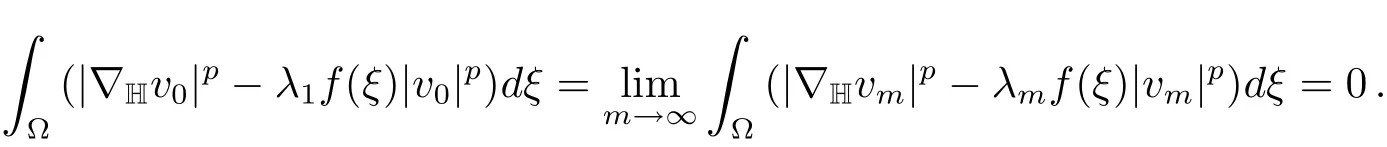
Since‖vm‖=1,we have‖v0‖=1.It then follows from Theorem 2.1 thatv0=φ1and a contradiction.Therefore{un}is bounded.

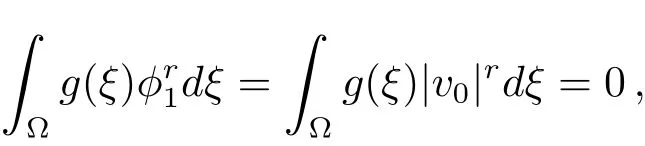
Thus we may assume,without loss of generality,thatum⇀u0.Then by analogous argument above on{um},it follows thatum→u0andu0=0.Moreover,and so the proof is complete.

5 The Case When λ＞λ1(f)

In this section,with the properties of Nehari manifold,we shall give simple proofs of the existence of two positive solutions,one inN−(λ)and the other inN+(λ).

Ifλ＞λ1(f),then

This yieldsφ1∈L−.Hence,φ1∈L−∩B−andN+(λ)/=Øif see,N(λ)may consist of two distinct components.Problems(1.1)–(1.2)have at least two positive solutions,if we show thatJλhas an appropriate minimizer on each component.

The following lemma provides a useful property of the positive solutions to our problem.＜0.As we shall

Proof Suppose that the result is false.Then there exist sequences{λm}and{um}

such that‖um‖=1,and

Since{um}is bounded,we assume without loss of generality thatum⇀u0inX.

We now show thatum→u0inX.Suppose otherwise,then‖u0‖and(f)implies that

which is a contradiction to(2.4).It follows from(5.1),(f)and(g)that

Using(i)and Theorem 2.1,we obtainu0=kφ1for some constantk.Hence,from(ii)we deduce thatk=0 which is impossible as‖u0‖=1.

(i)N0(λ)={0};

(ii)0∈/N−(λ)andN−(λ)is closed;

(iii)N−(λ)andN+(λ)are separated,i.e.,N−(λ)=Ø;

(iv)N+(λ)is bounded.

Proof (i)Supposeu0∈N0(λ){0},thenL0∩B0⊂L0∩B+=Ø.HenceN0(λ)={0}.

(ii)Suppose 0∈then there exists{um}⊆N−(λ)such thatum→0 inX.Hence

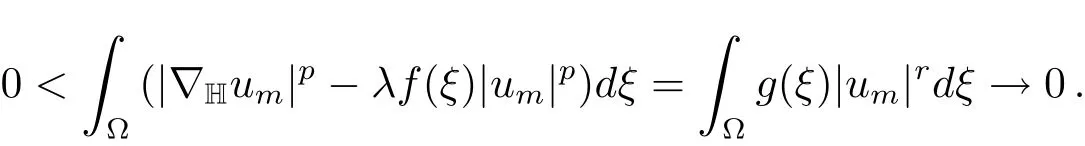
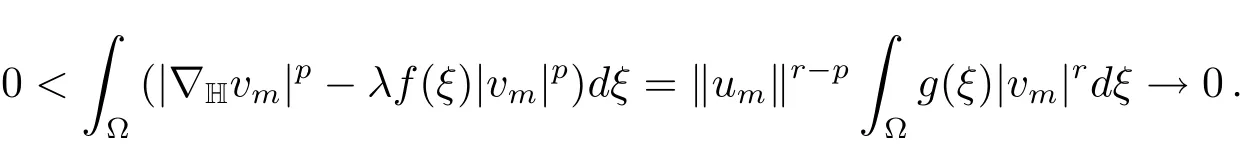
Thus by(f),we have

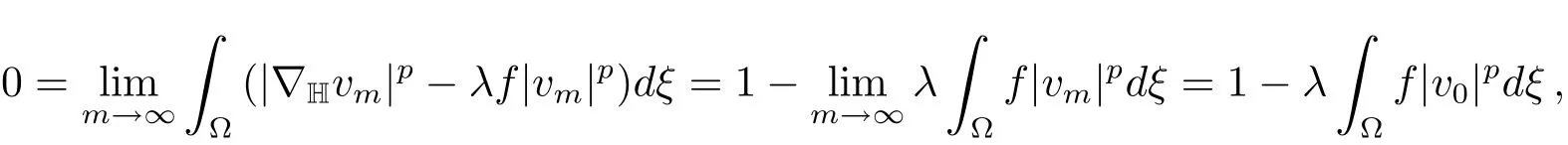
and thenv0/=0.Moreover,by the weak lower semicontinuity of the norm and(f),we get

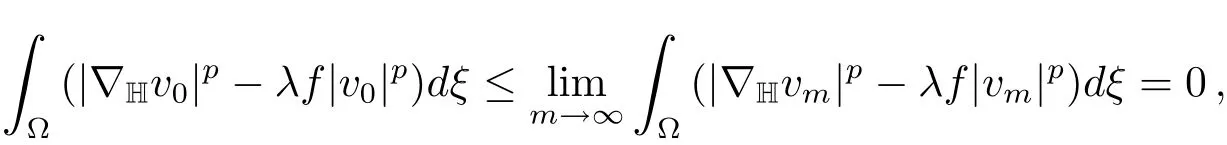
(iii)By(i)and(ii),

and thenN−(λ)andN+(λ)are separated.

(iv)Suppose thatN+(λ)is unbounded,then there exists{um}⊆N+(λ)such that‖um‖→∞asm→∞.By definition,

LetvmAccording to the above formula,we get

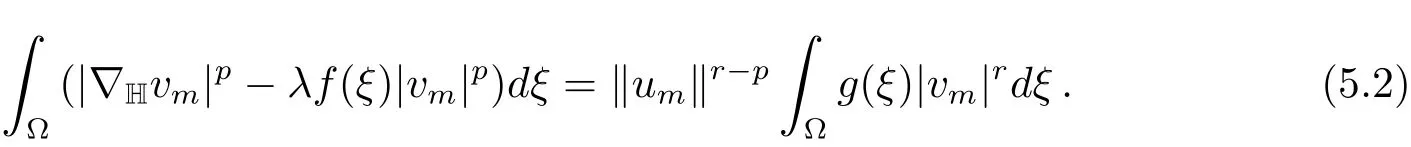
We can assume thatvm⇀v0inX.Since the left-hand side(l.h.s)of(5.2)is bounded but‖um‖→∞,it follows that|vm|rdξ=0.Then(g)implies=0.

Now we prove thatvm→v0inX.Suppose otherwise,then‖v0‖and

Sincevm→v0,we have‖v0‖=1.Hencev0∈B0and moreoverv0∈B+.By(f),we have

and thenv0∈L−.Thusv0which is again impossible.HenceN+(λ)is bounded.

WhenN−(λ)andN+(λ)are separated andN0(λ)={0},any non-zero minimizer forJλonN−(λ)(or onN+(λ))is also a local minimizer onN(λ)which is a critical point forJλonN(λ)and a solution of(1.1)–(1.2).

(i)every minimizing sequence forJλonN−(λ)is bounded;

(ii)infu∈N−(λ)Jλ(u)＞0;

(iii)there exists a minimizer ofJλonN−(λ).

Proof(i)Suppose that{um}∈N−(λ)is a minimizing sequence ofJλ.Then

wherec≥0.

Assume that{um}is unbounded,i.e.,‖um‖→∞asm→∞.Divided(5.3)by‖um‖pgives

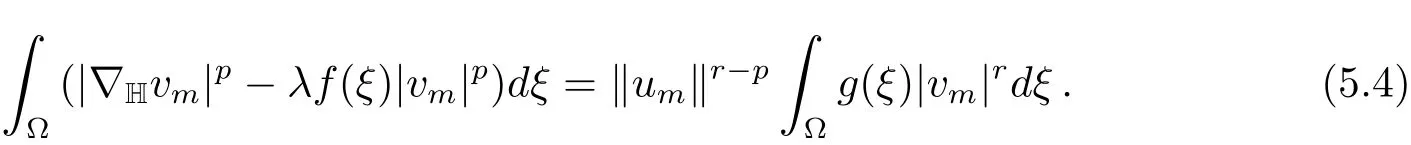
Since‖vm‖=1,we may assume thatvm⇀v0inX.Since the l.h.s of(5.4)is bounded,it follows thatdξ=0 and therefore

We now show thatvm→v0inX.Suppose otherwise,then

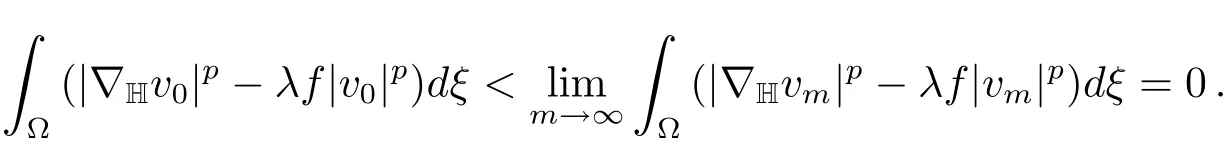
Thusv0/=0 andL−∩B0which is impossible.Hencevm→v0inX.It follows that‖v0‖=1.Moreover,by(f)

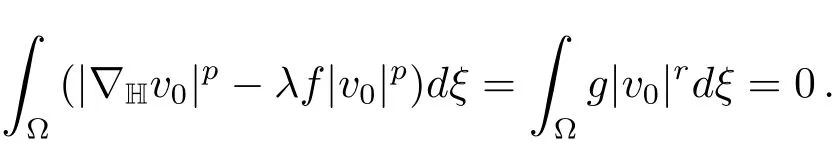
This implies thatv0∈L0∩B0which contradicts to the assumptionØ.Henceumis bounded.

(ii)SinceJλ(u)＞0 onN−(λ),we haveJλ(u)≥0.SupposeJλ(u)=0.Let{um}∈N−(λ)is a minimizing sequence,then

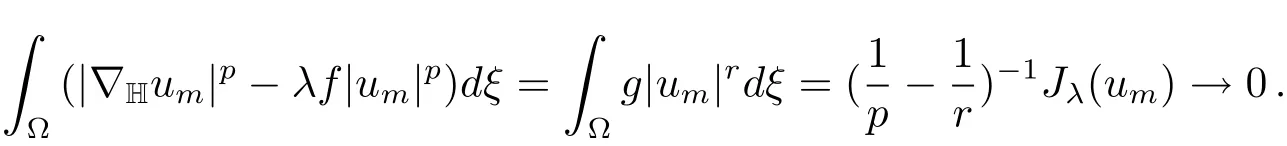
By(i)we know that{um}is bounded and we may supposeum⇀u0inX.By using exactly the same argument on{vm}in(i),it may be shown thatum→u0inX.By Theorem 5.1 we know thatand sou0/=0.It then follows exactly as in the proof in(i)thatand this contradicts the assumption

(iii)Let{um}∈N−(λ)is a minimizing sequence ofJλ,then

and then

By(i)we know that{um}is bounded.We may assume thatum⇀u0inX.Then by(g),we havedξ＞0 and soSince(L0∪L−)∩B+=Ø,it follows that⊆L+.HenceB+∩L+and−λf|u0|p)dξ＞0.

Furthermore,we havet(u0)u0∈N−(λ)wheret(u0)=

We will show thatum→u0inX.Suppose not,then

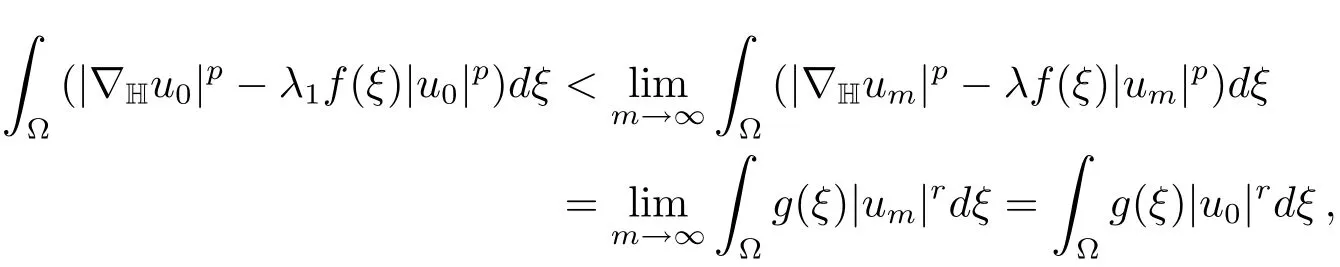
sot(u0)＜1.Sincet(u0)um⇀t(u0)u0and the map(tum)attains its maximum value att=1,we obtain

a contradiction.Henceum→u0.

We can easily deduce that

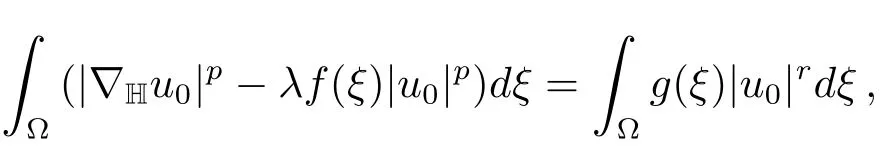
and thereforeu0∈N(λ).Sinceu0∈N−(λ).Also

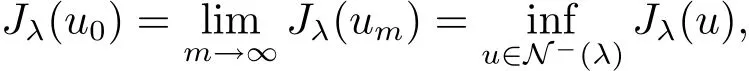
which impliesu0is a minimizer forJλ(u)onN−(λ).

We now turn our attention toN+(λ).

Theorem 5.3 SupposeL−is non-empty and=Ø,then there exists a minimizer ofJλ(u)onN+(λ).

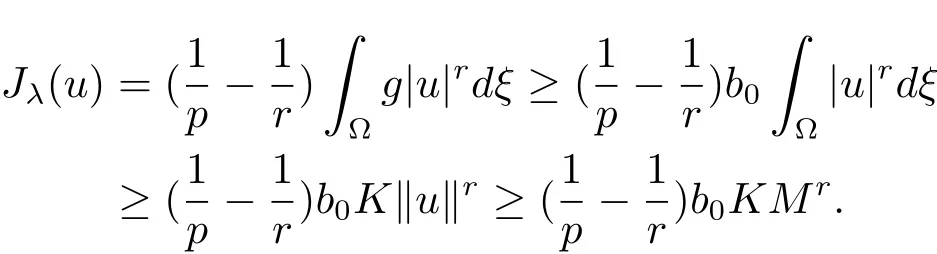
It follows thatJλ(u)is bounded from below onN+(λ)andJλ(u)exists.ClearlyJλ(u)＜0.Suppose that{um}⊆N+(λ)is a minimizing sequence ofJλ,then

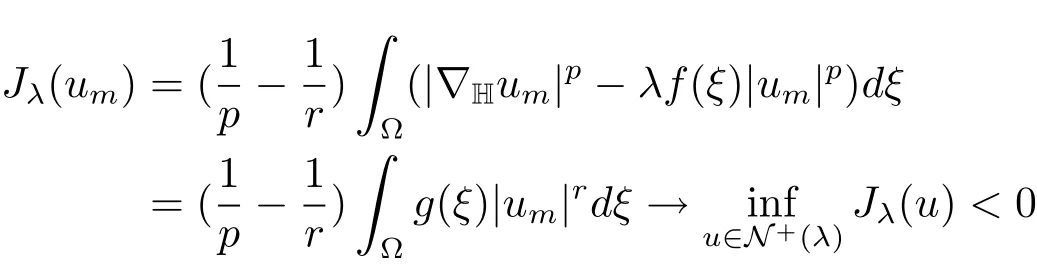
asm→∞.SinceN+(λ)is bounded,we may assumeum⇀u0inX.Then by(g)and(f),we have

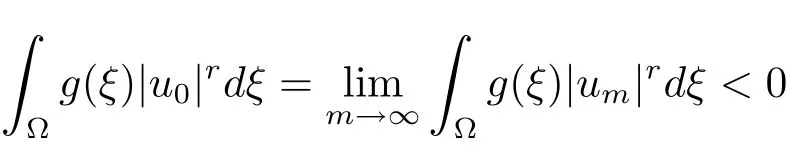
and

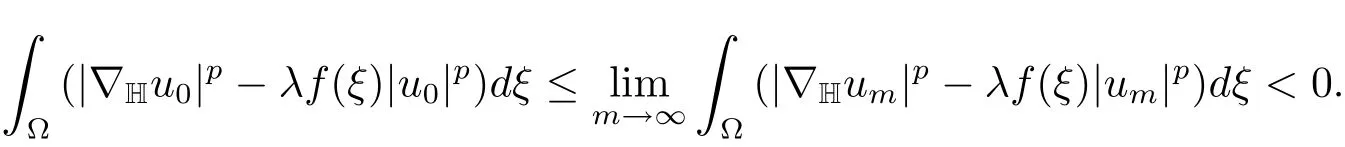
Supposeum/→u0inX.Then we get

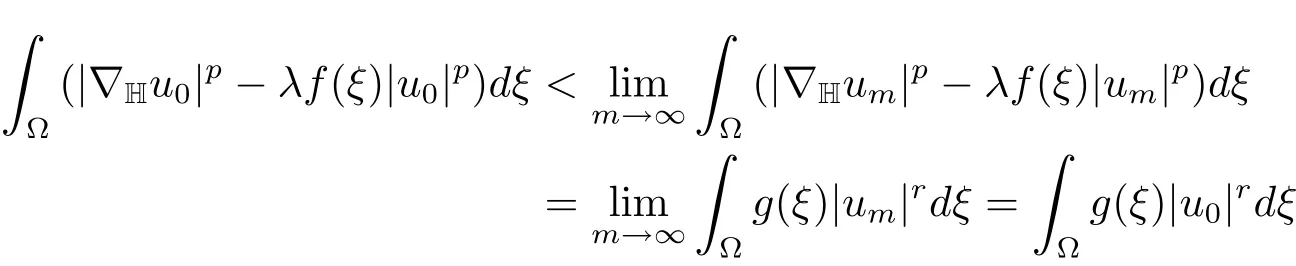
andt(u0)1.It follows thatJλ(t(u0)u0)≤Jλ(u0)＜J(u)and this is impossible.Henceu→uinX.We thus deduceλm0that

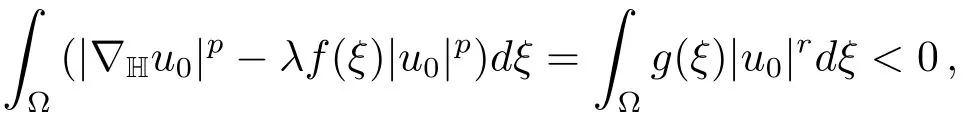
which showsu0∈N+(λ)and thenJλ(u0)=Jλ(u).Henceu0is a minimizer forJλ(u)onN+(λ)

Proof Sinceλ＞λ1(f),we have thatφ1∈L−.By Theorems 5.2 and 5.3,there exist minimizersofJλ(u)onN+(λ)andN−(λ),respectively.According to Theorem 5.1,N−(λ)andN+(λ)are separated andN0(λ)={0}.Hence there exist at least two minimizers which are local minimizers forJλonN(λ).These minimizers does not belong toN0(λ).Moreoverso we may assume≥0.By Lemma 3.1,are critical points ofJλonXand hence are weak solutions of(1.1)–(1.2).Finally,by the Harnack inequality[18],we obtain thatare positive solutions of(1.1)–(1.2).

Finally in this section,we investigate the nature ofN+(λ)asλ→

Theorem 5.4 Suppose point ofJλ(u)corresponding toλ=λm(we may assume thatum＞0).Then asm→∞,

(i)um→0;＜0,λm→andum∈N+(λ)is a critical

Proof(i)Sinceum∈N+(λ)is a critical point ofJλm(u),we have

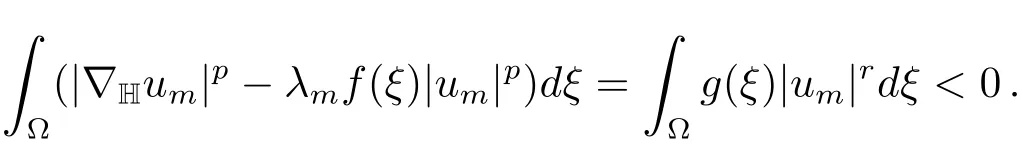
By Lemma 5.1 and Theorem 5.2,we getN+(λ)is bounded,and so is{um}.We may suppose thatum⇀u0inX.Supposeum/→u0,then

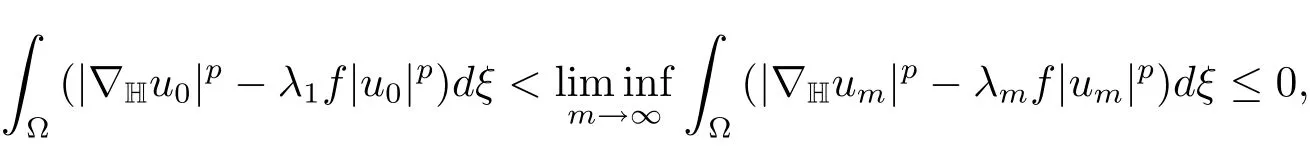
which is impossible because of(2.4).Henceum→u0asm→∞.This,together with(f)and(g),implies that

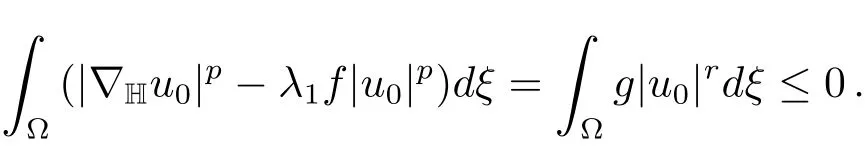
Combining with(2.4),it yieldsdξ=0.Thus by Theorem 2.1,we haveu0=kφ1for somek.But,as＜0,it follows thatk=0.Henceum→0 inX.

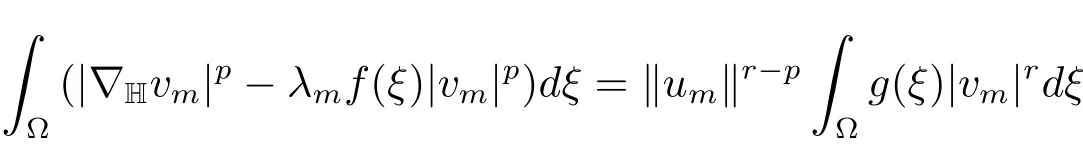
and so,since‖um‖→0,dξ=0.Supposevm/→v0,then‖v0‖and therefore＜0 which gives us a contradiction.Hencevm→v0,so‖v0‖=1 and=0.It then follows from Theorem 2.1 thatv0=φ1and the proof is completed.

[1]Stein E M.Harmonic analysis[M].Princeton:Princeton Univ.Press,1993.

[2]Bonfiglioli A,Lanconelli E,Uguzzoni F.Stratified Lie groups and potential theory for their sub-Laplacians[M].New York:Springer,2007.

[3]Alves C O,Hamidi A El.The Nehari manifold and existence of positive solutions to a class of quassilinear problems[J].Nonl.Anal.,2005,60(4):611–624.

[4]Fan Haining,Liu Xiaochun.Multiple positive solutions to a class of quasi-linear elliptic equations involving critical Sobolev exponent[J].Monatshefte F¨ur Mathematik,2014,174(3):427–447.

[5]Fan Haining,Liu Xiaochun.Multiple positive solutions for a class of quasi-linear elliptic equations involving critical sobolev exponent[J].Acta Math.Scientia:English,2014,34(4):1111–1126.

[6]Brown K J,Zhang Yangping.The Nehari manifold for a semilinear elliptic equation with a signchanging weight function[J].J.Diff.Equ.,2003,193(2):481–499.

[7]Brown K J,Wu Tsung-fang.Afibrering map approach to a semilinear elliptic boundary value problem[J].Electron.J.Diff.Equ.,2007,69:1–9.

[8]Brown K J.The Nehari manifold for a semilinear elliptic equation involving a sublinear term[J].Calc.Var.,2005,22(4):483–494.

[9]Drabek P,Pohozaev S I.Positive solutions for thep-Laplacian:Application of the fibering method[J].Proc.Roy.Soc.Edinburgh Sect.,1997,A127:703–727.

[10]Zhang Jinguo,Liu Xiaochun.The existence of solutions for a class of elliptic hemivariational inequality[J].J.Math.,2012,32(4):571–581.

[11]Luo Lin,Peng Shuangjie.The concentration behavior of the ground state solutions for Henon equation[J].J.Math.,2003,23(4):417–422.

[12]Bozhkov Y D,Mitodieri E.Existence of multiple solutions for quasilinear systems via Fibering Method[J].J.Diff.Equ.,2003,190(1):239–267.

[13]Dou Jingbo,Niu Pengcheng,Yuan Zixia.A Hardy inequality with remainder terms in the Heisenberg group and the weighted eigenvalue problem[J].J.Ineq.Appl.,2007,2(2):295–314.

[14]Huang Guangyue,Chen Wenyi.Inequalities of eigenvalues for bi-kohn laplacian on heisenberg group[J].Acta Math.Sci.,2010,30(1):125–131.

[15]Dou Jingbo,Han Yazhou.Eigenvalue problems of thep-sub-Laplacian with indefinite weight on the Heisenberg group[J].Adv.Math.,2011,40(6):687–696.

[16]Niu Pengcheng,Zhang Huiqing,Wang Yong.Hardy type and Rellich type inequalities on the heisenberg group[J].Proc.Amer.Math.Soc.,2001,129(12):3623–3630.

[17]Binding P A,Drabek P,Huang Yinxing.On Neumann boundary value problems for some quasilinear elliptic equations[J].Electron.J.Diff.Equ.,1997,5:1–11.

[18]Capogna L,Danielli D,Garofalo N.An embedding theorem and the Harnack inequality for nonlinear subelliptic equations[J].Comm.P.D.E.,1993,18:1765–1794.

[19]Folland G B,Stein E M.Estimates for the¯∂bcomplex and analysis on the Heisenberg group[J].Comm.Pure Appl.Math.,1974,27:429–522.

[20]Fuˇcik S,Kufner A.Nonlinear differential equations[M].Amsterdam:Elsevier,1980.

[21]Struwe M.Variational methods[M].New York:Springerr-Verlag,1984.

[22]Willem M.Minimax theorem[M].Berlin:Birkhauser,1996.