NOTES ON STRONGLY SEPARABLE EXTENSIONS

XU Ai-min

(School of Mathematical Sciences,Qufu Normal University,Qufu 273165,China)

1 Introduction

For any ring extensionϕ:R→S,we can always consider the triple of functors Γ =(S⊗R−,ϕ∗,HomR(RS,−)),whereS⊗R−and HomR(RS,−)are,respectively,the left and the right adjoint of the restriction of scalars functorϕ∗:S-Mod→R-Mod.The functorϕ∗is termed a quasi-Frobenius(Frobenius)functor ifS⊗R−and HomR(RS,−)are similar(naturally isomorphic).It was shown in[8](see[22])thatϕ∗is a quasi-Frobenius(Frobenius)functor if and only ifϕis a quasi-Frobenius(Frobenius)extension in the sense of[21](see[18]),i.e.,Sis finitely generated and projective as a leftR-module and the(S,R)-bimodulesSand HomR(RS,RR)are similar(i.e.,Sis finitely generated and projective as a leftR-module andS～=HomR(RS,RR)as(S,R)-bimodules).It was known[8]that ifϕis a quasi-Frobenius extension,then the functorsS⊗R−,ϕ∗and HomR(RS,−)are exact and preserve all limits and colimits as well as injective and projective objects.Separable extensions were studied in[10,14,16,17,19,23,27,28]among others.The ring extensionϕis separable[25]if the natural multiplication mapS⊗RS→Sis a split epimorphism asS-bimodules;ϕis separable if and only ifϕ∗is a separable functor in the sense of[23];ϕis split[25]ifϕis a split monomorphism ofR-bimodules;ϕis split if and only ifS⊗R−is a separable functor;ϕis called strongly separable[10]ifϕis a separable,split and quasi-Frobenius extension.Butϕis called strongly separable in[19]ifϕis a separable,split and Frobenius extension.And hence the notion of strongly separable extensions in[10]is weaker than that of[19].

Gorenstein homological algebra was initiated by Auslander and Bridger in[1,2],where they introduced theG-dimension of any finitely generated module over a two-sided Noetherian ring.Over a general ring,Enochs and Jenda[12]introduced Gorenstein projective modules,which is a generalization of finitely generated modules ofG-dimension zero.And to complete the analogy with the classical homological algebra,Gorenstein injective and fl at modules were introduced by Enochs et al.in[12,13].The Gorenstein homological dimensions are similar to(and refinements of)the classical homological dimensions.In 2004,Holm[15]generalized several well-known results on Gorenstein dimensions over Noetherian rings to arbitrary rings,and then the Gorenstein homological dimensions theory witnessed a new impetus.LetRbe a ring andMa leftR-module.We useGpd(M),Gid(M)andGfd(M)to denote,respectively,the Gorenstein projective,injective,and fl at dimensions ofM.In[5],several classical results on global homological dimensions were extended to global Gorenstein homological dimensions.Namely,it was proved in[5]that for a ringR,sup{Gpd(M)|Mis a leftR-module}=sup{Gid(M)|Mis a leftR-module}.The common value of the terms of this equality is called,the left Gorenstein global dimension ofR,and denoted byl.Ggldim(R).Also,the left Gorenstein weak global dimension of a ringR,l.wGgdim(R)=sup{Gfd(M)|Mis a leftR-module},is investigated.

Recall that an Artin algebraRis said to be of finite representation type if there exist only finitely many isomorphism classes of finitely generated indecomposableR-modules.It is well known that determining the representation type of algebras is fundamental and important in representation theory of Artin algebras.As an analogy of Artin algebras of finite representation type,recall that an Artin algebraRis calledCM- finite if there exist only finitely many isomorphism classes of finitely generated indecomposable Gorenstein projectiveR-modules.This notion was introduced by Beligiannis in[3].Since thenCM- finite Artin algebras have attracted considerable attentions[3,4].Recall from[9]that an Artin algebraRis calledCM-free if any finitely generated Gorenstein projectiveR-module is projective.Note thatCM-free algebras are an extreme case ofCM- finite algebras.

In this paper,we study the invariant properties under strongly separable extensions,such as the Gorenstein(weak)global dimensions,the representation type andCM- finite type of Artin algebras.In Section 2,we show that ifϕ:R→Sis a strongly separable extension,thenRandShave the same left global dimension,left weak global dimension,left Gorenstein global dimension.Moreover,ifSis right coherent,then they have the same left Gorenstein weak global dimension.Finally,it is proved that ifϕis a strongly separable extension of Artin algebras,thenRisCM- finite(resp.,CM-free,of finite representation type)if and only if so isS.

Throughout this paper,all rings are associative with identity and all modules are unitary.LetRbe a ring,R-Mod denotes the category of all leftR-modules.We writeRM(MR)to indicate a left(right)R-module.For anR-moduleM,we usepd(M)andfd(M)to denote,respectively,projective, fl at dimension ofM.lD(R)andwD(R),stand for the left global dimension,the weak global dimension of a ringR,respectively.addMdenotes the class of all direct summands of finite direct sums of copies ofM.LetM,Nbe two leftR-modules.IfMis a direct summand ofN,then we denote it byM|N.For unexplained concepts and notations,we refer the reader to[11,20,25,26].

2 Main Results

Definition 2.1[10]A ring extensionϕ:R→Sis called strongly separable ifϕis a separable,split and quasi-Frobenius extension.

Example 2.2[10,19](1)LetGbe a group with a subgroupHof finite index,sayn,ifRis a ring withnR=R,thenRGis a strongly separable extension ofRH.

(2)LetRbe any ring,then the ringMn(R)ofn×nmatrices overRis a strongly separable extension ofR.

(3)SupposeHis a finite dimensional,semisimple,cosemisimple Hopf algebra over a fieldK.IfAis anH-Galois extension ofS,thenAis a strongly separable extension ofS.

For a ring extensionϕ:R→S,we consider the following conditions

(C1)SY|S(S⊗RY)for everyY∈S-Mod.

(C2)Ris anR-bimodule direct summand ofS.

(C3)HomR(RS,−)preserve all projective objects,− ⊗RSandϕ∗preserve all injective objects.

(C4)RSandSRare finitely generated projective.

By[7,Lemma 3.1],we know that ifϕ:R→Sis separable,thenϕsatisfies(C1).And hence any strongly separable extensionϕ:R→Ssatisfies the conditions(C1)–(C4),there are some other examples satisfy the above conditions.For example,

(1)the extensionϕ:R→A⊗kF=S,whereRis a finite-dimensional algebra over a fieldk,andFa finite separable field extension ofkby[6,p.6,Lemma 1]and[24,p.275,Lemma 2.3].

(2)the extensionϕ:R→R∗G=S,whereRis any ring andGis a finite group such that|G|−1∈R.

Lemma 2.3 Letϕ:R→Sbe a ring extension with(C1)and(C4).IfMis a leftS-module,then we have

1.Mis a projective leftR-module if and only ifMis a projective leftS-module;

2.Mis a fl at leftR-module if and only ifMis a fl at leftS-module

Proof(1)IfMis a projective leftR-module,thenS⊗RMis a projectiveS-module and henceMis a projective leftS-module sinceSM|S(S⊗RM).Conversely ifMis a projective leftS-module,thenMis a projective leftR-module by(C4).

(2)IfMis a fl at leftS-module,then it is a fl at leftR-module sinceSis projective as a leftR-module.Conversely,assumeMis a fl at leftR-module,thenS⊗RMis a fl at leftS-module.ButSM|S(S⊗RM)and henceMis a fl at leftS-module.

Lemma 2.4 Letϕ:R→Sbe a ring extension with(C1)and(C4).IfMis a leftS-module,then we have

1.pd(SM)=pd(RM)=pd(S(S⊗RM));

2.fd(SM)=fd(RM)=fd(S(S⊗RM)).

Proof(1)By Lemma 2.3(1)we havepd(SM)≥pd(RM).By(C1),we getpd(S(S⊗R M))≥pd(SM).Ifpd(RM)=n＜∞,then there exists a projective resolution ofRM:

By(C4),we get a projective resolution of theS-moduleS⊗RM:

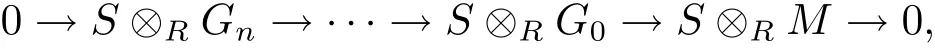
this impliespd(RM)≥pd(S(S⊗RM)),and hencepd(SM)=pd(RM)=pd(S(S⊗RM)).

(2)By Lemma 2.3(2),we havefd(SM)≥fd(RM).By(C1),we getfd(SM)≤fd(S(S⊗RM)).By(C4),we find thatfd(RM)≥fd(S(S⊗RM)),it follows thatfd(SM)=fd(RM)=fd(S(S⊗RM)).

The following theorem extends[19,Theorem 4.2].

Theorem 2.5 Letϕ:R→Sbe a ring extension with(C1),(C2)and(C4).ThenlD(R)=lD(S)andwD(R)=wD(S).

Proof By Lemma 2.4,we havelD(R)≥lD(S)andwD(R)≥wD(S).We now provelD(R)≤lD(S).For any leftR-moduleM,we haveRM|R(S⊗RM)by(C2),and hencepd(RM)≤pd(R(S⊗RM))=pd(S(S⊗RM))≤lD(S)by Lemma 2.4,that is,lD(R)≤lD(S).Similarly we havewD(R)≤wD(S).

By[7,Lemma 3.1],we get the following.

Corollary 2.6 Letϕ:R→Sa separable split ring extension with(C4),thenlD(R)=lD(S)andwD(R)=wD(S).

The following lemma is very useful for us.

Lemma 2.7 Letϕ:R→Sbe a ring extension with(C3)and(C4).

1.IfM∈R-Mod is Gorenstein projective(resp.Gorenstein flat),thenS⊗RMis Gorenstein projective(resp.Gorenstein flat).

2.IfM∈S-Mod is Gorenstein projective(resp.Gorenstein flat),thenRMis Gorenstein projective(resp.Gorenstein flat).

Proof(1)IfM∈R-Mod is Gorenstein projective,then we have an exact sequenceξ=···F−1→F0→F1→···of projectiveR-modules withM=ker(F0→F1)and such that it remains exact whenever HomR(−,P)is applied for every projectiveR-moduleP.SinceSis a fl at rightR-module,we get thatS⊗Rξis exact andS⊗RM=ker(S⊗RF0→S⊗RF1).We also get thatS⊗RFiis projective for everyi.Let us suppose finally thatP∈S-Mod is projective.Notice thatPis also a projectiveR-module by(C4)and HomS(S⊗RFi,P)～=HomR(Fi,HomS(S,P))～=HomR(Fi,P).ThusS⊗RMis Gorenstein projective.

IfM∈R-Mod is Gorenstein flat,then we have an exact sequenceξ=···F−1→F0→F1→···of fl atR-modules withM=ker(F0→F1)and such that it remains exact wheneverE⊗R−is applied for every injective rightR-moduleE.SinceSis a fl at rightR-module,we get thatS⊗Rξis exact andS⊗RM=ker(S⊗RF0→S⊗RF1).We also get thatS⊗RFiis fl at for everyi.Let us suppose finally thatE∈S-Mod is injective.Notice thatEis also an injectiveR-module by(C3)andE⊗SS⊗RFi～=E⊗RFi.ThusS⊗RMis Gorenstein flat.

(2)IfM∈S-Mod is Gorenstein projective,then we have an exact sequenceξ=···F−1→F0→F1→···of projectiveS-modules withM=ker(F0→F1)and such that it remains exact whenever HomS(−,P)is applied for every projectiveS-moduleP.EveryFiis a projective leftR-module by(C4).Let us suppose finally thatP∈RMod is projective.Notice that HomR(RS,P)is also a projectiveS-module by(C3)and HomS(Fi,HomR(RS,P))～=HomR(S⊗SFi,P)～=HomR(Fi,P).ThusMis a Gorenstein projectiveR-module.

IfM∈S-Mod is Gorenstein flat,then we have an exact sequenceξ=···F−1→F0→F1→···of fl atS-modules withM=ker(F0→F1)and such that it remains exact wheneverE⊗S−is applied for every injective rightS-moduleE.EveryFiis a fl at leftR-module by(C4).Let us suppose finally thatE∈R-Mod is injective.Notice thatE⊗RSis also an injectiveS-module by(C3)andE⊗RS⊗SFi～=E⊗RFi.ThusMis a Gorenstein flat leftR-module.

Lemma 2.8 Letϕ:R→Sbe a ring extension with(C1),(C2)and(C4).ThenRis right coherent if and only ifSis right coherent.

Proof LetRbe right coherent and{Mi|i∈I}a family of fl at leftS-modules.TheneveryMiis a flat leftR-module by(C4)andMiis a flatleftR-module.And henceS⊗RMiis a fl at leftS-module.SinceSMi|S(S⊗RMi),Miis a flat leftS-module which implies thatSis right coherent.Conversely,we suppose thatSis right coherent.Let{Mi|i∈I}be a family of flat leftR-modules.It is easy to see that(S⊗RMi)is a flat leftS-module.By(C4),it is also a fl at leftR-module.Note that(S⊗RMi)～=S⊗RMisinceSRis finitely presented.R(Mi)|R(S⊗RMi)by(C2).ThusMiis a flat leftR-module,and soRis right coherent.

Corollary 2.9 Letϕ:R→Sbe strongly separable,thenRis right coherent if and only ifSis right coherent.

We now give a Gorenstein version of Lemma 2.3.

Lemma 2.10 Letϕ:R→Sbe a ring extension with(C1),(C3)and(C4)andMbe a leftS-modules.

1.Mis a Gorenstein projective leftR-module if and only ifMis a Gorenstein projective leftS-module.

2.IfSis right coherent,thenMis a Gorenstein flat leftR-module if and only ifMis a Gorenstein flat leftS-module.

Proof(1)Assume thatRMis Gorenstein projective,thenS⊗RMis a Gorenstein projectiveS-module by Lemma 2.7.And henceSMis Gorenstein projective by[15,Theorem 2.5]and(C1).Conversely,it is immediate by Lemma 2.7.The corresponding proof for Gorenstein flat modules are analogous to that of(1).

Theorem 2.11 Letϕ:R→Sbe a ring extension.Then

1.Ifϕsatisfies(C1),(C3)and(C4),thenl.Ggldim(S)≤l.Ggldim(R).Moreover,ifϕalso satisfies(C2),thenl.Ggldim(S)=l.Ggldim(R).In particular,ifϕ:R→Sis a strongly separable extension,thenl.Ggldim(S)=l.Ggldim(R).

2.IfSis right coherent andϕsatisfies(C1),(C3)and(C4),thenl.wGgldim(S)≤l.wGgldim(R).Moreover,ifϕalso satisfies(C2),thenl.wGgldim(S)=l.wGgldim(R).In particular,ifSis right coherent andϕ:R→Sis a strongly separable extension,thenl.wGgldim(S)=l.wGgldim(R).

Proof(1)Suppose thatl.Ggldim(R)=m＜∞.LetSMbe anS-module.Thenl.Gpd(RM)≤m.So there exists a Gorenstein projective resolution ofRM:

whereGk,···,G0are Gorenstein projectiveR-modules.SinceS⊗RGiis a Gorenstein projectiveS-module for all 0≤i≤kby Lemma 2.7,we get a Gorenstein projective resolution of theS-moduleS⊗RM:

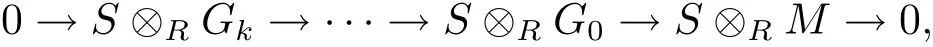
butSM|S(S⊗RM)by(C1).SoGpdS(SM)≤mby[15,Propositions 2.19].Thus

Ifϕalso satisfies(C2),suppose thatl.Ggldim(S)=n＜∞.LetRMbe anR-module.Thenl.GpdS(S⊗RM)≤n.So there exists a Gorenstein projective resolution ofS(S⊗RM):

whereGk,···,G0are Gorenstein projectiveS-modules.SinceRGiis a Gorenstein projectiveR-module for all 0≤i≤kby Lemma 2.7,we get a Gorenstein projective resolution of theR-moduleR(S⊗RM):

butRM|R(S⊗RM)by(C2).SoGpdR(RM)by Lemma[15,Propositions 2.19].Thusl.Ggldim(R)≤l.Ggldim(S)and hencel.Ggldim(R)=l.Ggldim(S).

(2)Suppose thatl.wGgldim(R)=m＜∞.LetSMbe anS-module.Thenl.Gfd(RM)≤m.So there exists a Gorenstein flat resolution ofRM:

whereGk,···,G0are Gorenstein flatR-modules.SinceS⊗RGiis a Gorenstein flatS-module for all 0≤i≤kby Lemma 2.7,we get a Gorenstein flat resolution of theS-moduleS⊗RM:

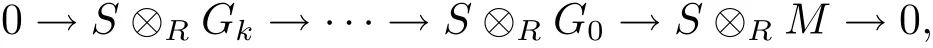
butSM|S(S⊗RM)by(C1).SoGfdS(SM)by[15,Propositions 3.13].Thus

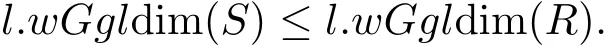
Ifϕalso satisfies(C2),suppose thatl.wGgldim(S)=n＜∞.LetRMbe anR-module.Thenl.GfdS(S⊗RM)≤n.So there exists a Gorenstein flat resolution ofS(S⊗RM):

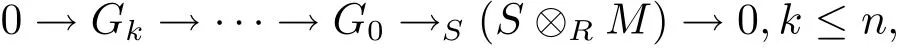
whereGk,···,G0are Gorenstein flatS-modules.SinceRGiis a Gorenstein flatR-module for all 0≤i≤kby Lemma 2.7,we get a Gorenstein fl at resolution of theR-moduleR(S⊗RM):butRM|R(S⊗RM)by(C2).SoGfdR(RM)≤nby Lemma and[15,Propositions 3.13].Thusl.wGgldim(R)≤l.wGgldim(S)and hencel.wGgldim(R)=l.wGgldim(S).

It is known that a ringRis quasi-Frobenius if and only ifl.Ggldim(R)=0,so we have

Corollary 2.12[10,Proposition 5.13]Letϕ:R→Sbe strongly separable,thenRis quasi-Frobenius if and only ifSis quasi-Frobenius.

For an Artin algebraR,letR-mod denote the category of finitely generated leftR-modules.Recall that a moduleM∈R-mod is called an additive generator forR-mod if any indecomposable module inR-mod is in addM.Obviously,an Artin algebraRis of finite representation type if and only ifR-mod has an additive generator.LetGp(R)be the full subcategory ofR-mod consisting of Gorenstein projective modules.Clearly,RisCM- finite if and only if there exists a moduleN∈R-mod such thatGp(R)=addN.

Theorem 2.13 Letϕ:R→Sbe a ring extension with(C1)–(C4).IfRandSare Artin algebras,then

1.RisCM-free if and only ifSisCM-free.

2.Ris of finite representation type if and only ifSis of finite representation type.

3.RisCM- finite if and only ifSisCM- finite.

Proof(1)LetRbeCM-free and letM∈S-mod be Gorenstein projective.ThenRMis Gorenstein projective by Lemma 2.7.SoRMis projective and henceSMis also projective by Lemma 2.3(1).ThusSisCM-free.Conversely,LetSbeCM-free andM∈R-mod be Gorenstein projective.ThenS(S⊗RM)is Gorenstein projective by Lemma 2.7.SoS(S⊗RM)is projective and henceR(S⊗RM)is also projective by Lemma 2.3.SinceRM|R(S⊗RM),RMis projective and soRisCM-free.

(2)LetRbe of finite representation type andM∈R-mod an additive generator forR-mod.It suffces to prove thatS⊗RMis an additive generator forS-mod.LetT∈S-mod be indecomposable.ThenT∈R-mod,T|Mnfor some positive integern.SoS⊗RT|(S⊗RM)n.It follows from(C1)thatT∈add(S⊗RM)asS-modules andS⊗RMis an additive generator forS-mod.Conversely,ifSbe of finite representation type,then there exists an additive generatorN∈S-mod forS-mod.It suffces to prove thatNis an additive generator forR-mod.LetT∈R-mod be indecomposable.It follows from(C2)thatT|S⊗RTasR-modules.Note thatS⊗RT|NnasS-modules for some positive integern,soS⊗RT|NnasR-modules andNis an additive generator forR-mod.

(3)The proof is similar to that of(2).

Corollary 2.14 Letϕ:R→Sbe a strongly separable extension of Artin algebras,thenRisCM-free(resp.,CM- finite,of finite representation type)if and only if so isS.

[1]Auslander M.Anneaux de Gorenstein,et torsion en alg`ebre commutative[M].Paris:Secr´etariat Math´ematique,1967,S´eminaire d’Alg`ebre Commutative dirig´e par Pierre Samuel,1966.

[2]Auslander M,Bridger M.Stable module theory[M].Memoirs Amer.Math.Soc.,1969.

[3]Beligiannis A.Cohen-Macaulay modules,(co)torsion pairs and virtually Gorenstein algebras[J].J.Alg.,2005,288:137–211.

[4]Beligiannis A.On algebras of finite Cohen-Macaulay type[J].Adv.Math.,2011,226:1973–2019.

[5]Bennis D,Mahdou N.Global gorenstein dimension[J].Proc.Amer.Math.Soc.,2010,138(2):461–465.

[6]Bonami L.On the structure of skew group rings[M].Algebra Berichte 48,Munchen:Verlag Reinhard Fisher,1984.

[7]Caenepeel S,Zhu Bin.Separable bimodules and approximation[J].Alg.Rep.The.,2005,8:207–223.

[8]Casta˜no F,Nˇastˇasescu C,Vercruysse J.Quasi-Frobenius functors,applications[J].Comm.Alg.,2010,38:3057–3077.

[9]Chen Xiaowu.Algebras with radical square zero are either self-injective or CM-free[J].Proc.Amer.Math.Soc.,2012,140:93–98.

[10]Cunningham R S.Strongly separable pairings of rings[J].Tran.Amer.Math.Soc.,1970 148(2):399–416.

[11]Enochs E E,Jenda O M G.Relative homological algebra[M].Berlin,New York:Walter de Gruyter,2000.

[12]Enochs E E,Jenda O M G.Gorenstein injective and projective modules[J].Math.Z.,1995,220(4):611–633.

[13]Enochs E E,Jenda O M G,Torrecillas B.Gorenstein flat modules[J].J.Nanjing Univ.Math.Biquart.,1993,10:1–9.

[14]Hirata K,Sugano K.On semisimple extensions and separable extensions over non-commutative rings[J].J.Math.Soc.Japan,1966,18(4):369–372.

[15]Holm H.Gorenstein homological dimensions[J].J.Pure Appl.Algebra,2004,189:167–193.

[16]Kadison L.On split,separable subalgebras with counitality condition[J].Hokkaido Math.J.,1995,24:527–549.

[17]Kadison L.New examples of Frobenius extensions[M].University Lecture Series 14,Providence RI:Amer.Math.Soc.,1999.

[18]Kasch F.Projektive Frobenius-Erweiterungen[M].Sitzungsber Heidelb.Akad Wiss,1960.

[19]Kadison L.The Jones polynomial and certain separable Frobenius extensions[J].J.Alg.,1996,186:461–475.

[20]Meng Fanyun,Sun Juxiang.Cotorsion pairs over finite graded rings[J].J.Math.,2015,35(2):227–236.

[21]Müller B.Quasi-Frobenius-Erweiterungen[J].Math.Z.,1964,85:345–368.

[22]Morita K.Adjoint pairs of functors and Frobenius extensions[J].Sc.Rep.T.K.D.A.,1965,9:40–71.

[23]N˘ast˘asescu C,Van den Bergh M,Van Oystaeyen F.Separable functors applied to graded rings[J].J.Alg.,1989,123:397–413.

[24]Passman D.S.The algebraic structure of group rings[M].New York.Wiley-Interscience 1977

[25]Pierce R.Associative Algebras[M].Berlin.Springer Verlag 1982.

[26]Rotman J.J.An introduction to homological algebra[M].New York:Academic Press,1979.

[27]Sugano K.Note on semisimple extensions and separable extensions[J].Osaka J.Math.,1967,4:265–270.

[28]Sugano K.Separable extensions and Frobenius extensions[J].Osaka J.Math.,1970,7:291–299.