A NONTRIVIAL PRODUCT OFIN THE COHOMOLOGY OF THE STEENROD ALGEBRA

WANG Chong,LIU Xiu-gui

(1.College of Mathematical and Statistics,Cangzhou Normal University,Cangzhou 061001,China)

(2.School of Mathematical Sciences,Nankai University,Tianjin 300071,China)

1 Introduction

To determine the stable homotopy groups of spheres is one of the most important problems in algebraic topology.So far,several methods were found to determine the stable homotopy groups of spheres.For example,we have the classical Adams spectral sequence(ASS)(see[1])based on the Eilenberg-MacLane spectrumKZp,whoseE2-term is(Zp,Zp)and the Adams differential is given bywhereAdenotes the modpSteenrod algebra.There are three problems in using the ASS:calculation ofE2-termcomputation of the differentials and determination of the nontrivial extensions fromE∞to the stable homotopy groups of spheres.So,for computing the stable homotopy groups of spheres with the classical ASS,we must compute theE2-term of the ASS,(Zp,Zp).

Throughout this paper,pdenotes an odd prime andq=2(p−1).The known results onare as follows.is trivial by its definition.From[2],(Zp,Zp)has Zp-basis consisting ofa0∈(Zp,Zp),hi∈(Zp,Zp)for alli≥ 0 and(Zp,Zp)has Zp-basis consisting ofα2,(i＞0),gi(i≥ 0),ki(i≥ 0),bi(i≥0),andhihj(j≥i+2,i≥0)whose internal degrees are 2q+1,2,piq+1,pi+1q+2piq,qandpiq+pjq,respectively.In 1980,Aikawa[3]determined(Zp,Zp)byλ-algebra.

Studying higher-dimensional cohomology of the modpSteenrod algebraAwas an interesting subject and studied by several authors.For example,Liu and Zhao[4]proved the following theorems,respectively.

Theorem 1.1Forp≥11 and 4≤s＜p,the product/=0 in the classical Adams spectral sequence,wherewas given in[5].

In this paper,our main result can be stated as follows.

Theorem 1.2 Letp≥7,and 0≤s＜p−5.Then in the cohomology of the modpSteenrod algebraA,the product(Zp,Zp)is nontrivial,where

The main method of proof is the(modified)May spectral sequence,so we will recall some knowledge on the May spectral sequence in Section 2.After detecting the generators of some MayE1-terms in Section 3,we will prove Theorem 1.2.

2 The May Spectral Sequence

As we know,the most successful method to compute(Zp,Zp)is the MSS.From[6],there is a May spectral sequence(MSS)which converges to(Zp,Zp)withE1-term

whereE()is the exterior algebra,P()is the polynomial algebra,and

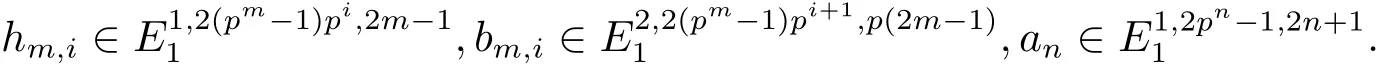
One has

and ifx∈andy∈then

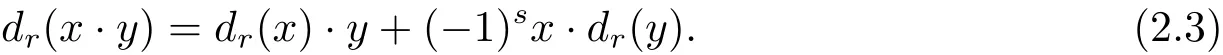
In particular,the first May differentiald1is given by

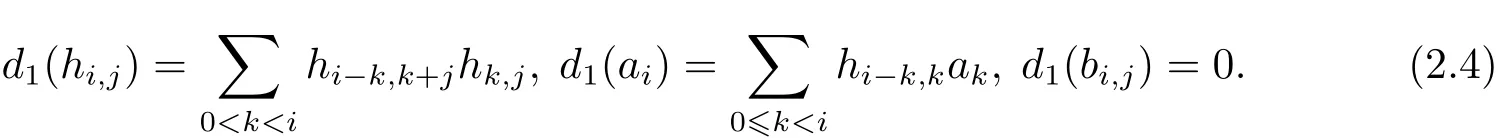
There also exists a graded commutativity in the MSS:

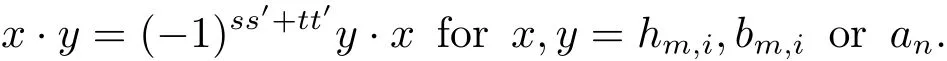
For each elementx∈we define dimx=s,degx=t,M(x)=u.Then we have that

wherei≥1,j≥0.

Note that by the knowledge on thep-adic expression in number theory,for each integert≥ 0,it can be expressed uniquely ast=q(cnpn+cn−1pn−1+···+c1p+c0)+e,where 0≤ci＜p(0≤i＜n),p＞cn＞0,0≤e＜q.

3 Proof of Theorem 1.2

Before showing Theorem 1.2,we first give some important lemmas which will be used in the proof of it.The first one is a lemma on the representative of˜δs+4in the May spectral sequence.

Lemma 3.1 Forp≥7 and 0≤s＜p−4.Then the fourth Greek letter element(Zp,Zp)is represented by

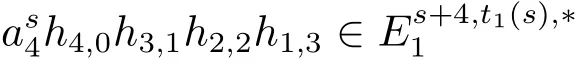
in theE1-term of the May spectral sequence,whereis actuallydescribed in[6]andt1(s)=q[(s+1)+(s+2)p+(s+3)p2+(s+4)p3]+s.

By(2.2),we know that to prove the non-triviality of(Zp,Zp),we have to show that the representative of the product cannot be hit by any May differential.For doing it,we give the following two lemmas.

Lemma 3.2 Letp≥7,0≤s＜p−5.Then we have the MayE1-term

wheret(s,n)=q[(s+1)+(s+5)p+(s+3)p2+(s+4)p3]+s,and

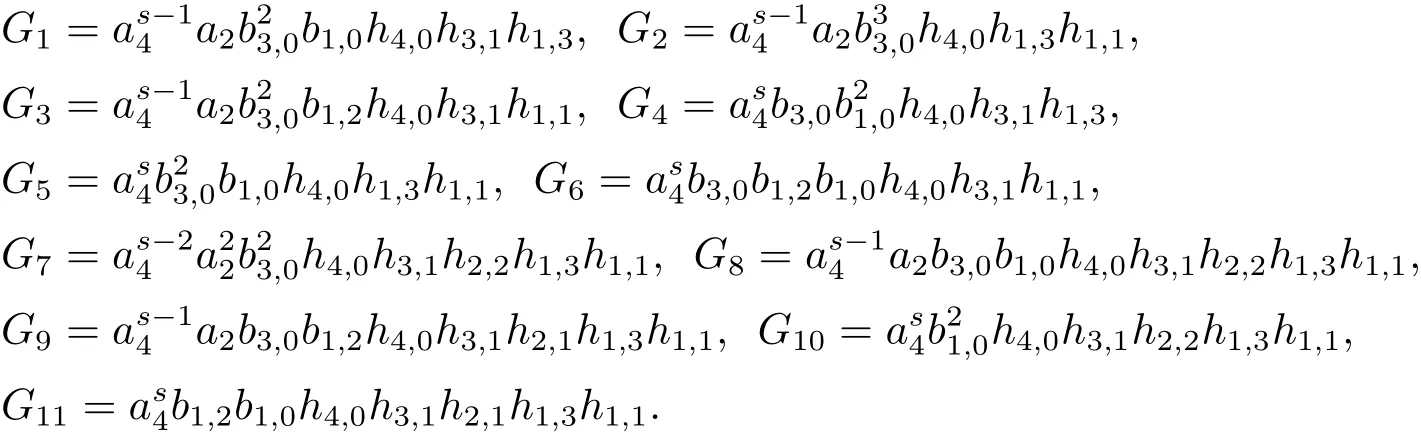
For the convenience of writing,we make the following rules:

(i)ifi＞j,we putaion the left side ofaj;

(ii)ifj＜k,we puthi,jon the left side ofhw,k;

(iii)ifi＞w,we puthi,jon the left side ofhw,j;

(iv)apply the rules(ii)and(iii)tobi,j.

Now we give the proof of the above lemma.

Proof The proof of this lemma is divided into the following six cases.Consider

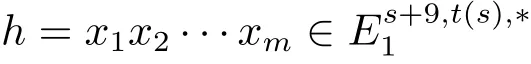
in the MSS,wherexiis one ofak,hr,jorbu,z,0≤k≤4,0≤r+j≤4,0≤u+z≤3,r＞0,j≥0,u＞0,z≥0.By(2.5),we can assume that degxi=q(ci,3p3+ci,2p2+ci,1p+ci,0)+ei,

whereci,j=0 or 1,ei=1 ifxi=akiorei=0.It follows that dim=s+9 and

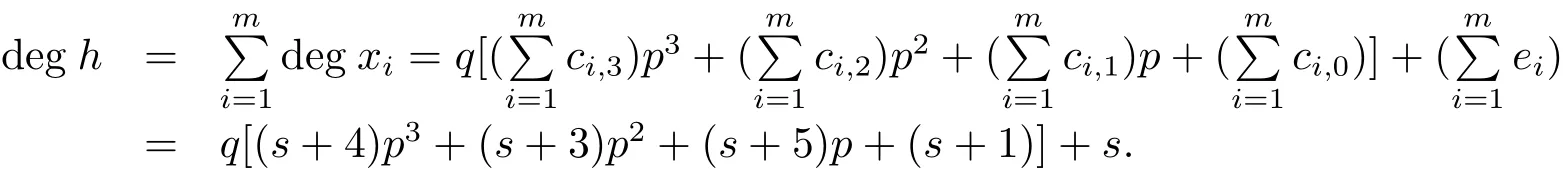
Note that

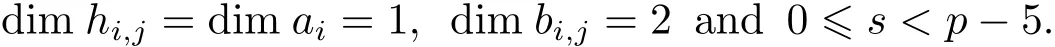
Using 0≤s+5,s+4,s+3,s+1,s＜pand the knowledge on thep-adic expression in number theory,we have that

Byci,2=0 or 1,one hasm≥s+4 from=s+4.Note thatm≤s+9.Thusmmay equals+4,s+5,s+6,s+7,s+8 ors+9.Since=s,deghi,j≡0(modq)(i＞0,j≥0),degai≡1(modq)(i≥0)and degbi,j≡0(modq)(i＞0,j≥0),then by the graded commutativity ofand degree reasons,we can assume thath=withh′=xs+1xs+2···xm,where 0 ≤x,y,z,k,l≤s,x+y+z+k+l=s.Consequently,we have

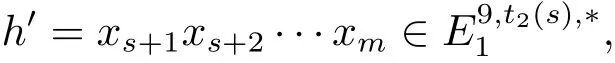
wheret2(s)=q[(s+4−l)p3+(s+3−l−k)p2+(s+5−l−k−z)p+(s+1−l−k−z−y)].From(3.1),we have

By the reason of dimension,all the possibilities ofh′can be listed as whereyiis in the form ofhr,jwith 0≤r+j≤4,r＞0,j≥0 andziis in the form ofbu,zwith 0≤u+z≤3,u＞0,z≥0.

Case 1m=s+4.Soh′=xs+1xs+2xs+3xs+4∈and it is impossible to exist.Thenhdoesn’t exist either.

Case 2m=s+5.From=s+4−lin(3.2),we have thatl=s+4−s−1.Thusl=s−1 orsandh′=y1z1···z4∈We list all the possibilities in Table 1.

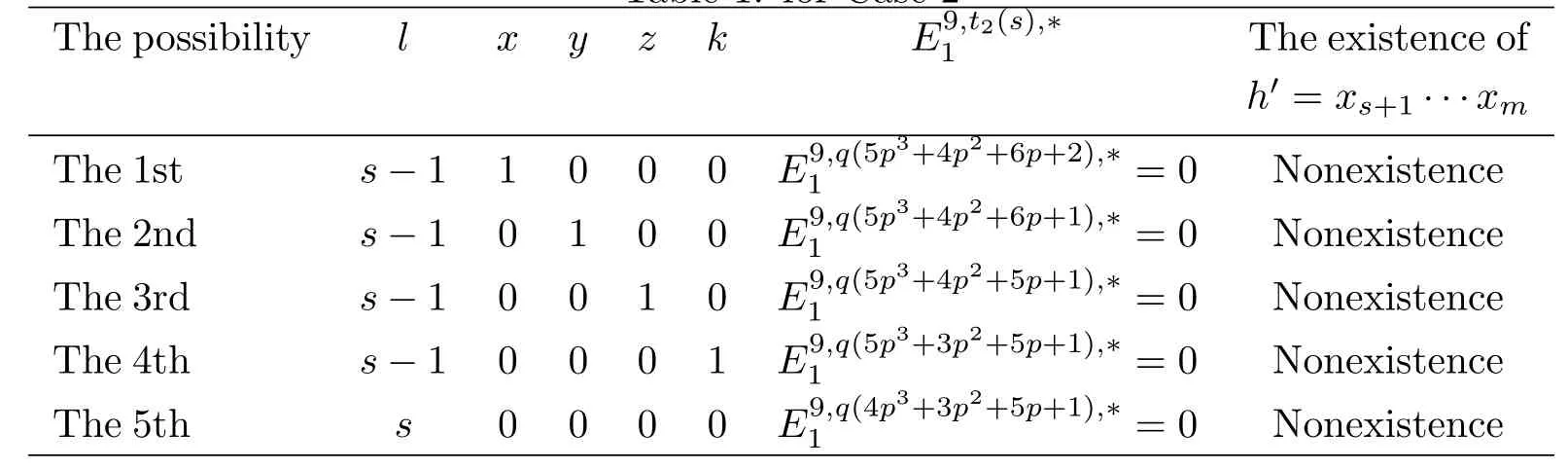
Table 1:for Case 2

Case 3m=s+6.Fromci,3=s+4−lin(3.2),we have thatl=s+4−≥s−2.Thusl=s−2,s−1 orsandWe list all the possibilities in Table 2.

In the table,denoted by g1,g2,g3,g4,g5,g6,respectively.Consequently,in this case up to signdenoted by G1,G2,G3,G4,G5,G6,respectively.

Case 4m=s+7.Fromci,3=s+4−lin(3.2),we have thatl=s+4−c≥i,3s−3.Thusl=s−3,s−2,s−1 ors,andh′=y1···y5z1z2∈Whenl=s−3,we

have thatt2(s)=q[7p3+···].In this case,h′is impossible to exist.Thenhdoesn’t exist either.Next we list all the rest of possibilities in Table 3.

Table 2:for Case 3

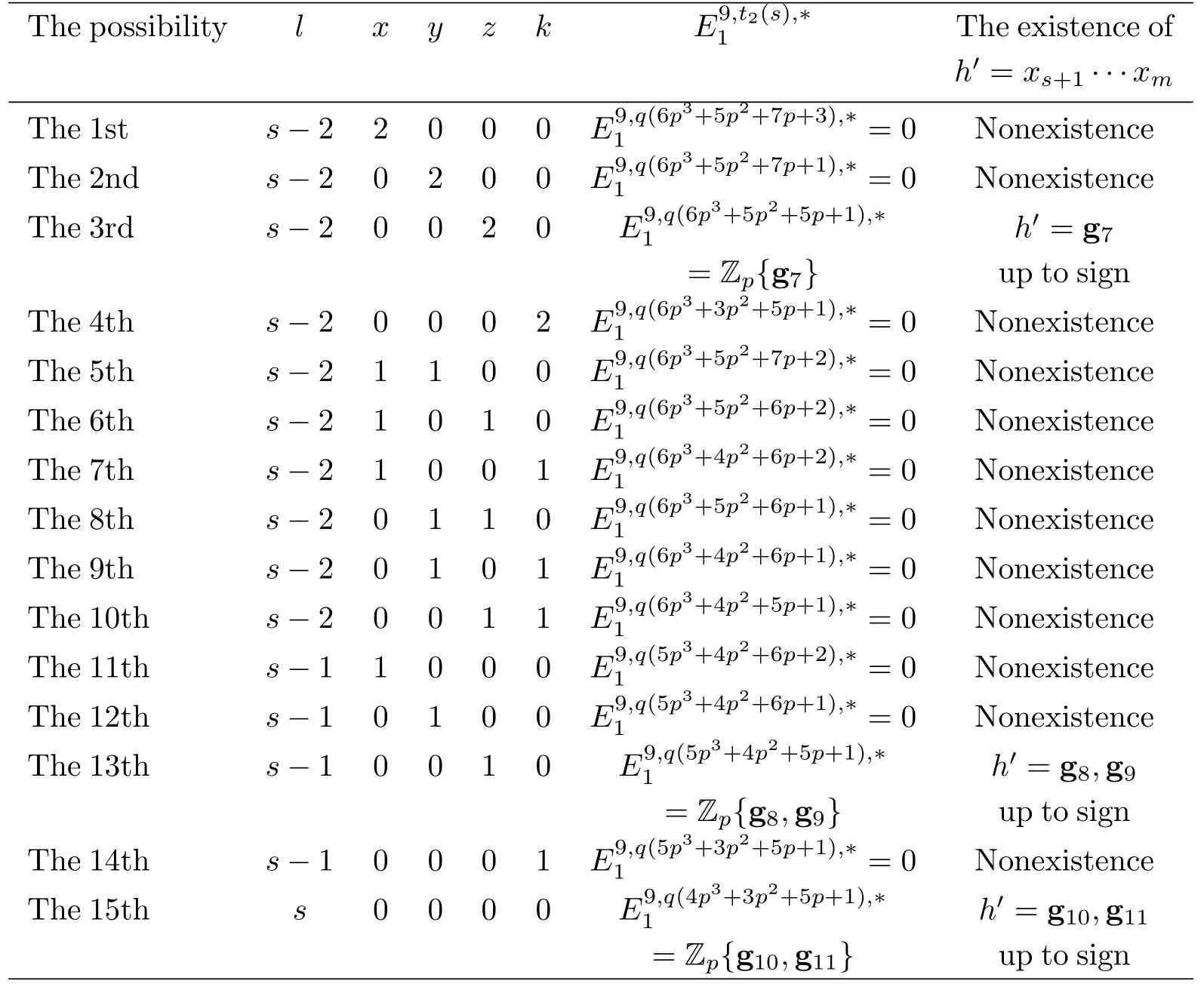
Table 3:for Case 4

In the tableh4,0h3,1h2,2h1,3h1,1,b3,0b1,0h4,0h3,1h2,2h1,3h1,1,b3,0b1,2h4,0h3,1h2,1h1,3h1,1,h4,0h3,1h2,2h1,3h1,1,b1,2b1,0h4,0h3,1h2,1h1,3h1,1,denoted by g7,g8,g9,g10,g11,respectively.Consequently,in this case up to signh=denoted by G7,G8,G9,G10,G11,respectively.

Case 5m=s+8.From=s+4−lin(3.2),we have thatl=s+4−s−4.Thusl=s−4,s−3,s−2,s−1 ors,andh′=y1···y7z1∈Whenl≤s−2,the coeあcient ofP3∈t2(s)is＞5.In these cases,h′is impossible to exist.Thenhdoesn’t exist either.Next we list all the other possibilities in Table 4.

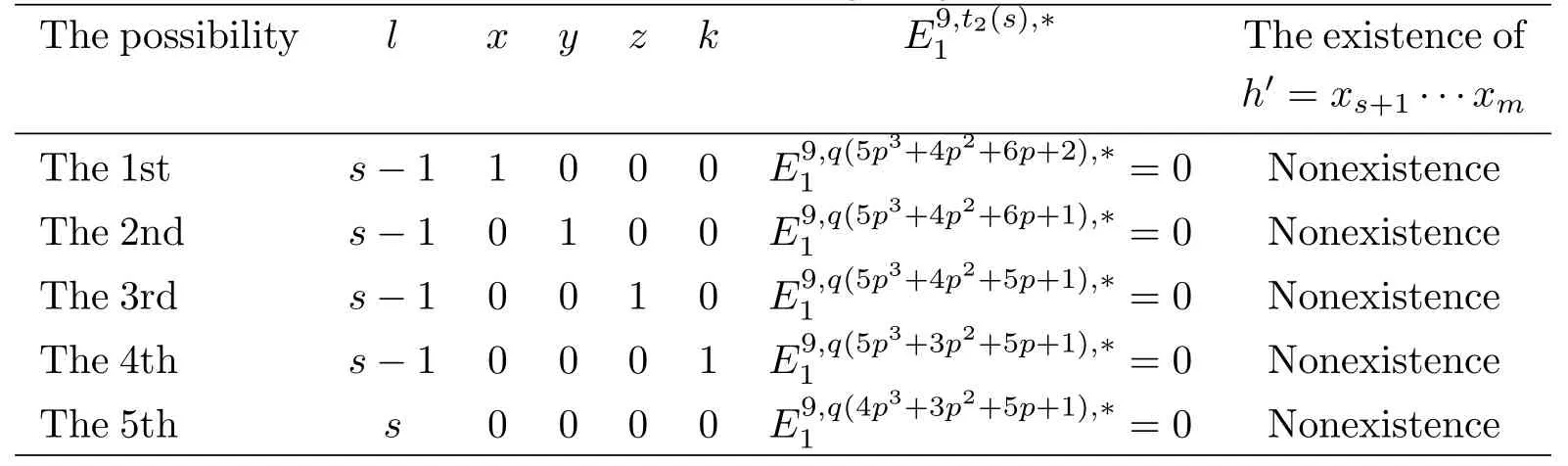
Table 4:for Case 5

Case 6m=s+9.Fromci,3=s+4−lin(3.2),we have thatl=s+4−c≥i,3s−5.Thusl=s−5,s−4,s−3,s−2,s−1 ors,andh′=y1···y9∈Whenl≤s−1,the coeあcient ofP3∈t2(s)is ≥ 5.In these cases,h′is impossible to exist.Thenhdoesn’t exist either.In the last possibility,t2(s)=4p3+3p2+5p+1,soh4,0,h3,1,h2,2,h1,3∈h′,h′is impossible to exist in this case by the reason of dimension.Thenhdoesn’t exist either.

Combining Cases 1–6 above,we obtain thatThis completes the proof of Lemma 3.2.

(2)For the eleven generators ofwe have that

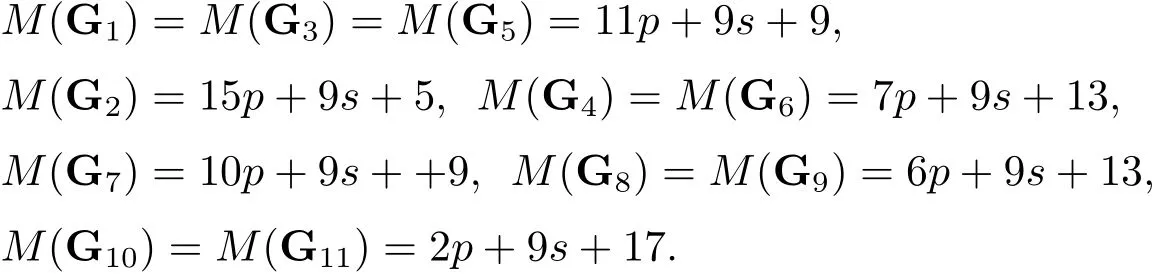
Moreover,we have thatM()=3p+9s+16.

Proof(1)Since it is known thatb1,iandare all permanent cycles in the MSS as[7]and converge nontrivially tobi,(Zp,Zp)for 0≤s＜p−5andi≥0,respectively(cf.Lemma 3.1),then∈is a permanent cycle in the MSS and converges to(Zp,Zp).

(2)From(2.5),the result follows by direct calculation.

Now we give the proof of Theorem 1.2.

Proof of Theorem 1.2From Lemma 3.3(1),(Zp,Zp)is represented byin the MSS.Now we will show that nothing hits the permanent cycleunder the May diあerentialdrforr≥ 1.From Lemma 3.2,we have=Zp{G1,G2,···,G11}.

For the generators G1,G3and G5whose May fi ltration are

(see Lemma 3.3),by the reason of May fi ltration,from(2.2)we see that

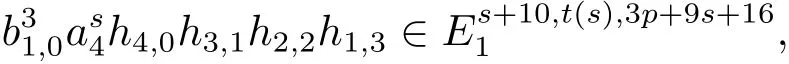
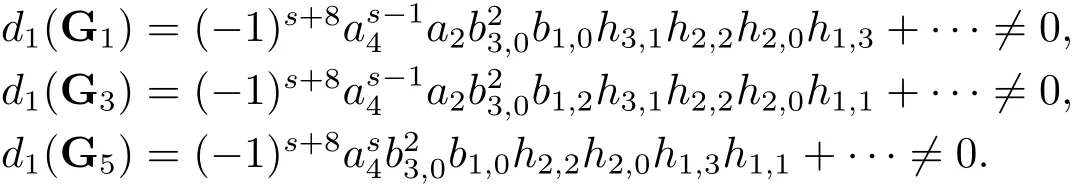
It is easy to see that the fi rst May diあerentials of G1,G3and G5are linearly independent.Consequently,the cocycle ofmust be zero.This means that=0 forr≥2,from which we have that

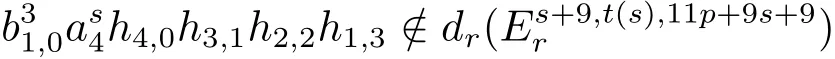
forr≥2.In all,forr≥1.

For the generator G2with May fi ltrationM(G2)=15p+9s+5(see Lemma 3.3),by an easy calculation,from(2.3)and(2.4),we have the fi rst May diあerentials of G2as follows

For the generators G4and G6whose May fi ltration areM(G4)=M(G6)=7p+9s+13(see Lemma 3.3),by the reason of May fi ltration,from(2.2)we see thatandi≥0,respectively(cf.Lemma 3.1),then∈is a permanent cycle in the MSS and converges to(Zp,Zp).

(2)From(2.5),the result follows by direct calculation.

Now we give the proof of Theorem 1.2.

Proof of Theorem 1.2From Lemma 3.3(1),(Zp,Zp)is represented byin the MSS.Now we will show that nothing hits the permanent cycleunder the May diあerentialdrforr≥ 1.From Lemma 3.2,we have=Zp{G1,G2,···,G11}.

For the generators G1,G3and G5whose May fi ltration are

(see Lemma 3.3),by the reason of May fi ltration,from(2.2)we see that

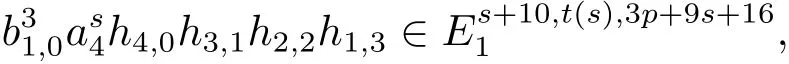
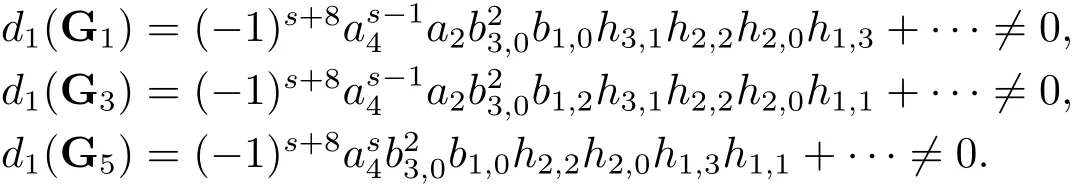
It is easy to see that the fi rst May diあerentials of G1,G3and G5are linearly independent.Consequently,the cocycle ofmust be zero.This means that=0 forr≥2,from which we have that

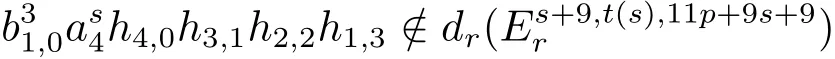
forr≥2.In all,forr≥1.

For the generator G2with May fi ltrationM(G2)=15p+9s+5(see Lemma 3.3),by an easy calculation,from(2.3)and(2.4),we have the fi rst May diあerentials of G2as follows

For the generators G4and G6whose May fi ltration areM(G4)=M(G6)=7p+9s+13(see Lemma 3.3),by the reason of May fi ltration,from(2.2)we see that

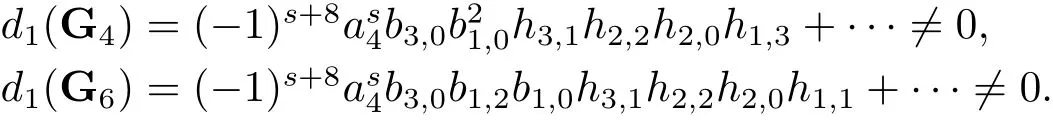
It is easy to see that the first May differentials of G4and G6are linearly independent.Consequently,the cocycle ofmust be zero.This means that

forr≥2,from which we have that∈/dr()forr≥2.In all,∈/dr()forr≥1.

For the generator G7with May filtrationM(G7)=10p+9s+9(see Lemma 3.3),by an easy calculation,from(2.3)and(2.4)we have the first May differentials of G7as follows

Finally,for the generators G8and G9whose May filtration areM(G8)=M(G9)=6p+9s+13(see Lemma 3.3),by the reason of May filtration,from(2.2)we see thatwhich represents(Zp,Zp)in the MSS is not indrforr≥1.

The discussion of G10and G11whose May filtration areM(G10)=M(G11)=2p+9s+17 is just like the analysis about G10and G11.

From the above discussion,we see the permanent cyclecannot be hit by any May differential in the MSS.Thus,converges nontrivially to(Zp,Zp)in the MSS.Consequently，This finishes the proof of Theorem 1.2.

Remark For further study on the typesetting based on English-Chinesesome special techniques,we may refer to[1–7].

[1]Adams J F.Stable homotopy and generalised homology[M].Chicago:University of Chicago Press,1974.

[2]Liulevicius.A.The factorizations of cyclic reduced powers by secondary cohomology operations[J].Mem.Amer.Math.Soc.,1962,42:978–981.

[3]Aikawa.T.3-dimensional cohomology of the modpSteenrod algebra[J].Math.Scand.,1980,47:91–115.

[4]Liu Xiugui,Zhao Hao.On a product in the classical Adams spectral of sequence[J].Pro.Amer.Math.Soc.,2009,137(7):2489–2496.

[5]Wang Xiangjun,Zhen Qibing.The convergence of[J].China Ser.A,1998,6:622–628.

[6]Ravenel D C.Complex cobordism and stable homotopy groups of spheres[M].Orlando:Academic Press,1986.

[7]Liu Xiugui.A nontrivial product in the stable homotopy groups of spheres[J].Sci.China Ser.A,2004,47(6):831–841.