气缸体对船舶柴油机模型精度的影响
2018-01-15唐元元张均东贾宝柱沈浩生
唐元元, 张均东, 贾宝柱, 沈浩生
(大连海事大学 轮机工程学院,辽宁 大连 116026)
计算机仿真拥有许多优点,但是仿真模型结构不合理、精度过低也会导致仿真结果可信度低、无实用价值的问题。对仿真实时性有一定要求的情况,内燃机模型一般选择使用平均值模型、零维模型或者其变种。在内燃机建模中一般将内燃机模型划分为涡轮增压器子模型、空冷器子模型、扫气总管子模型、气缸子模型、排气总管子模型五个部分。船用二冲程柴油机的建模依然沿用这套划分方法。对于二冲程柴油机,从扫气总管到气缸之间具有一个由气缸体、气缸、活塞、活塞杆填料函组成的容积。该容积随着活塞的运动而变化,对扫气空气有挤压、抽吸作用。在挤压和抽吸过程中,高温的气缸壁对这部分空气进行加热,影响扫气空气的热力状态。如果未考虑气缸体结构的影响,则气缸扫气温度与空冷器出口温度基本一致,低于实际的进气温度。扫气空气的状态严重影响柴油机的换气效果和进气量,影响模型的计算精度。对长行程、低转速二冲程柴油机的影响更为明显。因此,在建模过程中有必要考虑这部分结构,确保机理模型的完整性,提高模型的计算精度。
柴油机模型研究过程中面临着模型计算速度、计算精度、机理特征以及对实验数据的依赖程度之间的矛盾。Nikzadfar K等借鉴BOM建模方法,将柴油机模型划分为半静态模型和动态模型两部分,并在此基础上使用神经网络建立缸内性能模型和排放模型。建立的模型在满足计算精度的情况下,极大的减少了计算机运算量[1]。Finesso R等通过反推之前所建立的缸内燃烧模型中放热率、缸内压力与喷油率之间的关系,可以以较小的计算量获得较高的喷油量预测精度[2]。Sakellaridis N F等采用一种基于物理原理的meanline models建立了涡轮增压器模型[3]。实现了使用有限的数据图谱预测涡轮增压器全转速范围内的性能。Murphy A J等通过研究不同复杂度的气体特性及组份模型对气体温度随时间变化的影响以及对热力学效率的影响来提高模型精度[4]。Maroteaux F等将燃烧阶段气缸单区模型改进为双区模型,获得了满意的气缸压力及NOx排放精度,仿真结果的平均相对误差低于[5]2%。韩恺等使用GT-POWER软件采用DoE方法和神经网络方法建立的内燃机模型具有计算速度快、模型精度高、模型对测试数据依赖程度小的特点[6]。以上建模方法是通过混合多种建模技术、细化模型特性以及融合神经网络等方法来缓和柴油机建模过程中面临的模型计算速度、计算精度、机理特征以及对实验数据的依赖程度之间的矛盾。这些研究工作是针对柴油机部件或者非大型船用二冲程柴油机的建模研究。没有考虑针对船用二冲程柴油机的特定结构来提高柴油机整机性能参数的预测精度。
本文根据船用大型二冲程柴油机的结构特点,基于常用的柴油机零维建模方法,在扫气总管模型与燃烧室模型之间增加了气缸体模型并进行了对比仿真分析。通过仿真计算及数据对比,分析了气缸体容积对各个子模型的性能参数及仿真值精度的影响,并对影响机理进行了解释。
1 整机组件划分分析
在柴油机建模方法中,零维模型以曲轴转角作为计算步长,可以详细地描述缸内过程。平均值模型以时间为计算步长,以6~10个缸内循环的平均值作为柴油机缸内状态,无法描述缸内过程。在这些模型中,模型均是按照气体流动路径建立。船用柴油机建模时考虑的子部件主要包括涡轮增压器、空冷器、进气总管、燃烧室、排气总管,其结构如图1所示。不同种类的机型,如汽油机、安装EGR设备的发动机等,其发动机整机模型会在此基础上增减或者修改部分部件子模型。
船用二冲程直流扫气柴油机的燃烧室及外围组件的结构如图2所示,从图中可知,船用二冲程柴油机在气流通路上的部件除了燃烧室与进气总管之间的气缸体之外,其他结构均可采用图1所示的结构进行简化描述。
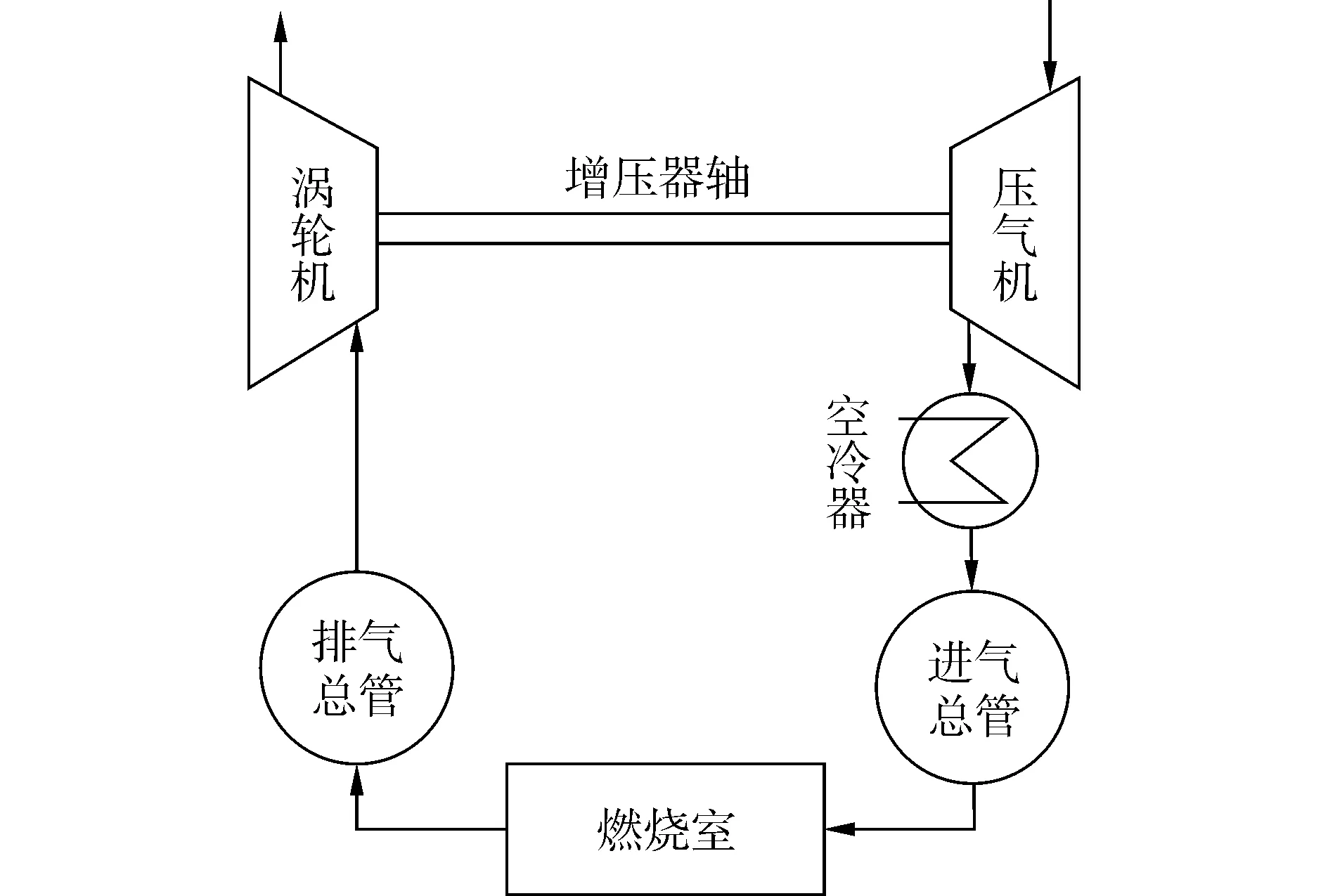
图1 柴油机模型结构Fig.1 Structure diagram of diesel model
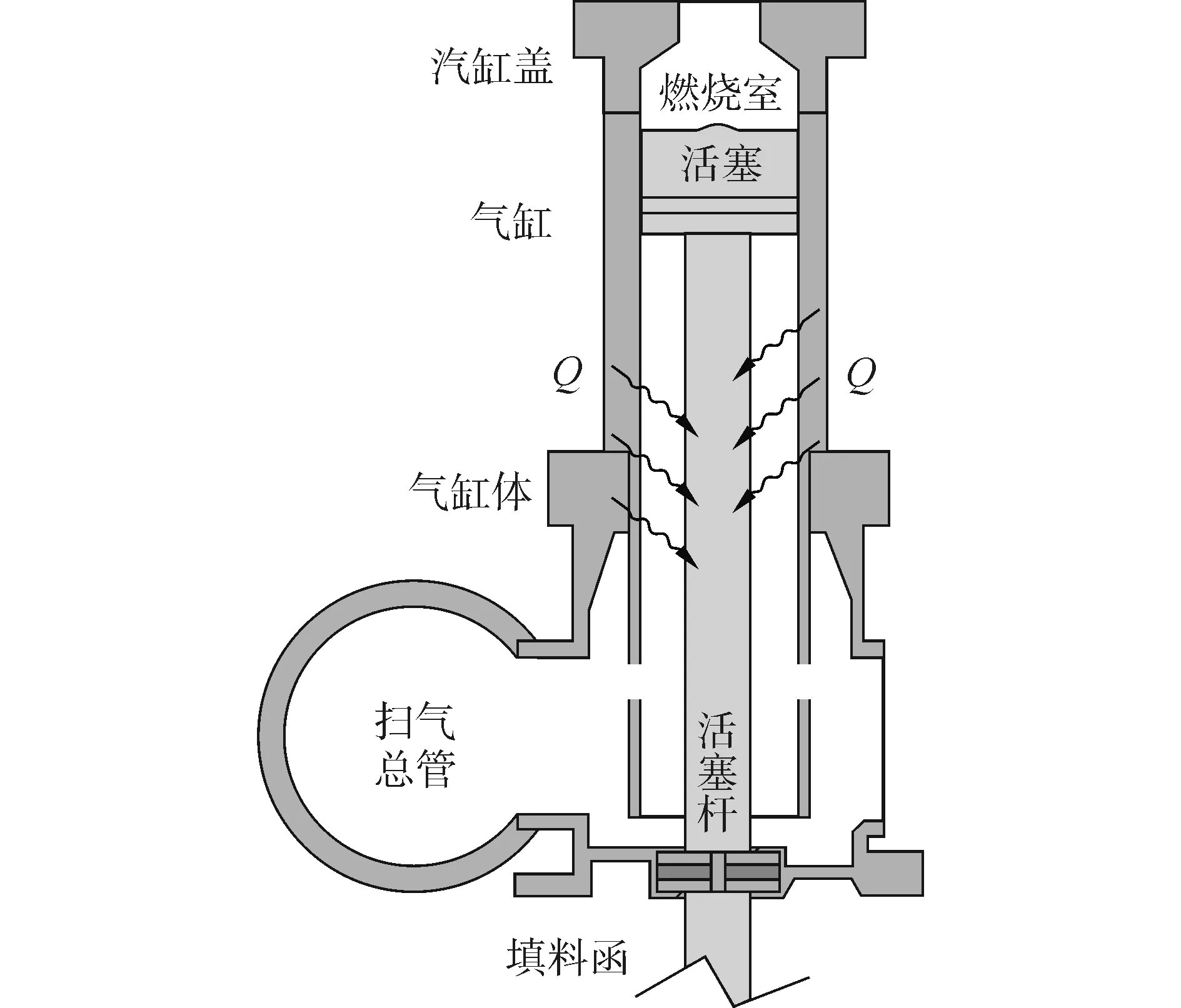
图2 气缸体结构Fig.2 Structure of cylinder body
从图2中还可以看出,活塞将气缸分为上下两部分容积。其中活塞、气缸、气缸盖围成的容积构成燃烧室容积,活塞、活塞杆填料函、气缸、气缸体构成另一部分容积,即气缸体容积。气缸下端通流面积大,在建模时可将气缸下方的容积与气缸体作为一个随着活塞运动而周期性变化的容积处理。当活塞在扫气口之上时,活塞下方的气缸容积通过气缸下端及气缸扫气口与气缸体容积相通,活塞上方的气缸容积封闭不与气缸体相通,增压空气不能进入燃烧室;当活塞在扫气口下方时,活塞下方的气缸容积通过气缸下端与气缸体相通,活塞上方的气缸容积通过扫气口与气缸体容积相通,增压空气通过扫气口流入燃烧室。活塞下行时,气缸体内容积变小,压力升高;活塞上行时,气缸体内容积变大,压力降低。对于短行程柴油机,活塞在上下止点时气缸体的容积比较小;对于长行程、超长行程柴油机气缸体容积比较大,对柴油机的性能影响明显。因此,二冲程柴油机建模时气流通路上增加气缸体子模型,如图3所示。
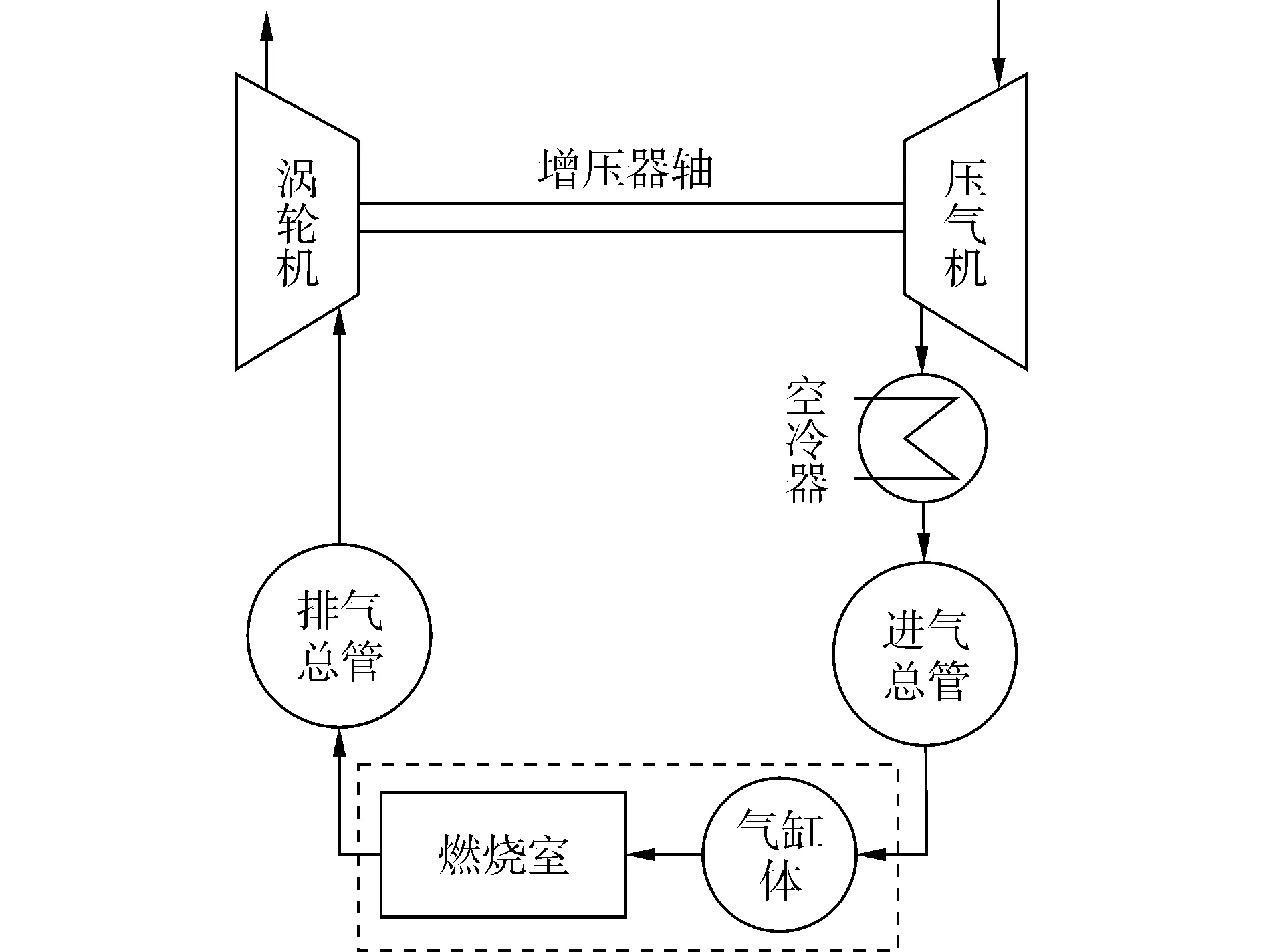
图3 改进的柴油机模型结构Fig.3 Structure diagram of modified diesel model
2 组件建模理论
基于热力学原理的柴油机模型具有非常好的理论基础,变量物理意义明确,校准后的模型计算精度高、机理响应合理。这类模型可用于辅助柴油机设计,预估柴油机性能[7],可以对柴油机的性能参数进行分析,如油耗、输出扭矩、排气温度、进气压力等。
2.1 进排气系统
本文中进排气系统包括进气总管容积、排气总管容积。这些容积是一个开式的热力学系统,在仿真计算中容积大小不变。进气总管接受经空冷器冷却降温的增压空气,在气缸体容积变化时补充或者吸收气缸体容积内的空气。排气总管接受每个气缸的高温脉冲废气,经排气总管稳压后驱动涡轮增压器。进气总管中的气体温度和环境温度差别并不大,计算过程中一般不考虑进气总管的散热作用。排气总管中的废气温度很高,全负荷运行时在400 ℃上下,计算过程中通常需要考虑排气总管的散热作用。
2.2 气缸体容积
由图2可知,气缸体容积始终与扫气总管相连,在扫气口打开时气缸体容积与燃烧室相通,在扫气口关闭时气缸体容积与燃烧室隔断。因此,建模时,气缸体容积根据柴油机在不同的工作冲程可以划分为两种的热力学系统。扫气过程中气缸体作为变体积开口系统处理,其他冲程中气缸体作为变体积半开半闭系统处理。气缸体容积变化期间,伴随着气缸壁对气缸体中工质的加热、气缸体壁与气缸体内工质之间的热量交换以及活塞与气缸体工质之间的功交换。根据能量守恒及质量守恒方程,在整个柴油机工作循环中,气缸体的热力状态可以统一表示为
(1)
(2)
在气缸体容积中工质均为新鲜空气,将工质作为理想气体处理,比内能u可以简化为温度T的函数,即
u=u(T)
(3)
于是可以得到
(4)
根据理想气体比内能的定义有
(5)
因此可以得出单位时间内温度的变化为
(6)
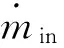
2.3 涡轮增压系统
涡轮增压系统由涡轮机、压气机以及连接它们的轴组成。高温高压的废气经过涡轮机后废气中焓值降低,降低的焓值转换为轴功并通过转轴驱动压气机旋转。高速旋转的压气机对环境空气增压,经冷却降温后送入气缸。增压空气可以提高柴油机的经济性及比功率。废气驱动涡轮机产生的功率为
(7)

(8)
式中:Ta为环境温度,下标c表示此参数为压气机参数。经压气机增压后工质温度会升高,压气机出口的工质温度为
(9)
在计算压气机的流量和效率时会用到涡轮增压器厂商提供的压气机图谱。图谱提供的数据没有覆盖压气机运行的低速区域,需要对低速区域进行外插值。标准的外插值方法不能有效的解决此问题,Dinescu和Tazerout采用量纲分析方法来解决此问题[8]。其中定义了三个无量纲参数:流量系数、圆周马赫数、等熵功系数。流量系数定义为
(10)
式中:d为压气机叶轮半径,ωtc为增压器转速,ρ为进压气机前的空气密度,下标cor表示标准条件下的换算值。圆周马赫数定义为
(11)
式中:k为绝热指数,R为气体常数。等熵功系数定义为
(12)
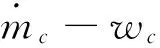
(13)
ηc=M(b1Φ2+b2Φ+b2)
(14)
式中a、b为系数。应用这些无量纲参数,压气机模型可以在整个转速范围内计算。
我访问的国家已经超过了35个,但在过去7年里,我把大部分时间都花在了探索越南少数民族文化上。我仍然会每年去一次印度和古巴。最近,我去婆罗洲拜访了巴瑶族人,在那里待了一个星期。因为无法与当地人交流,我感到很沮丧。游客们也经常在这里潜水,可我甚至很难找一艘船接近巴瑶族人,但我喜欢这个地方,我还会再去的。
2.4 空冷器模型
空冷器连接压气机出口和进气总管入口。船用柴油机的空冷器与压气机、进气总管的连接管路长度短、管路口径大,可以认为空冷器中进口压力与压气机出口压力是一致的,空冷器出口压力与进气总管进口压力一致。空冷器进、出口的压力和温度按照固定的压阻损失和散热系数简化计算。
2.5 气缸模型
气缸模型用于计算柴油机在扫气、压缩、燃烧、膨胀、排气过程中燃烧室内工质的成分、工质的热力状态、活塞的指示功、气缸的废气能量等。主要包括燃烧模型、气缸散热模型、气阀气口模型、排放模型。燃烧模型以Vibe燃烧模型、双Vibe燃烧模型、AVL MCC模型、Vibe双区模型应用较多。本文的研究工作在建模时使用双Vibe燃烧模型。双Vibe燃烧模型能更加精确的描述柴油机气缸内的燃油热释放率。模型把燃烧过程分为预混合燃烧和扩散燃烧两个阶段,总的燃烧质量分数等于预混合燃烧和扩散燃烧的质量分数之和,即
(15)
式中β为预混合燃烧的份数。燃烧过程中预混合燃烧和扩散燃烧的燃料分数、燃烧起始角、预混合燃烧领先角、燃烧持续角等参数对放热率曲线影响较大。柴油机在不同工况下,具有不同的放热率曲线。
气缸散热模型以Woschni散热模型应用较多。散热模型采用牛顿换热公式,核心是散热系数的计算。文中散热模型使用AVL 2000散热模型,该模型在Woschni散热公式的基础上改进。Woschni 1990散热公式与Woschni 1978散热公式相比,提高了柴油机低负荷下的计算精度[9]。AVL 2000散热模型认为,柴油机在换气过程中的热传递对容积效率有很大的影响,此影响对于低速柴油机更为明显[10]。在换气过程中散热系数计算公式为
(16)
式中:αw为按照Woschni公式计算的散热系数,D为缸径,p为气缸压力,T为气缸温度,Dm为进气口的直径,vin进气口工质的速度。
3 模型建立及校准
3.1 模型建立
本文以某型大功率超长行程二冲程船用柴油机作为母型机,研究柴油机模型在考虑气缸体容积和未考虑气缸体容积时对仿真模型的计算精度及性能变化趋势的影响。母型机的基本参数如表1所示,其中气缸的性能参数值为主机运行于最大持续功率(MCR)工况时各缸的平均值。

表1 柴油机技术参数(MCR)Table 1 Specifications of diesel engine(MCR)
柴油机模型可以使用编程软件从基础数学关系式开始编写,也可以借助柴油机模拟仿真平台,简化程序设计过程,直接对模型进行仿真分析。AVL BOOST是一款使用简单、运用广泛的柴油机建模仿真软件平台,能够进行柴油机整机性能循环仿真、后处理和噪声分析。软件采用模块化的方法建模,降低了对柴油机研究人员的计算机编程技能的要求同时节省了建模时间。研究人员可以将更多的精力放在对柴油机结构和性能的分析上。IMPRESS Chart可以实现结果分析、处理、导出等多项功能。
由于当前测量技术及大型船用柴油机实验条件的限制,在一般实验室条件下不能获得其精确的设计参数。因此,在BOOST建模中,不确定的组件参数先使用经验值,在校验过程中,再根据仿真结果和实验数据进行调整。基于研究目的,为了方便参数调整所建立的气缸模型使用完全相同的参数计算。根据在BOOST中搭建的柴油机模型,以活塞位于上止点为0°曲轴转角,气缸体容积随曲轴转角的变化关系如图4所示。气缸体与扫气总管及燃烧室直接相连,其容积变化的大小对扫气总管中的压力波动影响较大。

图4 各缸的气缸体容积Fig.4 Volume of cylinder body of each cylinder
3.2 模型校准
二冲程低速船用柴油机主要作为船舶主推进柴油机,主推进柴油机几乎在整个生命周期中运行于持续服务功率工况点。根据设计时的功率储备以及船舶使用情况,持续服务功率一般为约定最大持续功率(CMCR)的85%~90%。在柴油机性能分析和模型校准时,本文优先考虑80%和100%负荷工况点。校准后的柴油机模型计算结果与柴油机测试数据的对比如表2所示。

表2 模型主要参数校准结果
根据表2的仿真结果可知,校准后的柴油机模型计算精度很高。主机功率、扫气压力、排气温度三项指标基本与测试数据一致。爆发压力在高负荷时的仿真计算精度较高,低负荷时有一定的精度偏差,精度在5%以内。由校准结果可知:所建立的柴油机模型各项性能指标与实测值基本相符,并且所建立的模型满足本文仿真分析的要求。
4 仿真结果与讨论
在柴油机模型建好并校准后再将此模型的气缸体容积子模型去掉,作为原模型的对比模型。其他子部件模型及参数均与前一个柴油机模型一致。在本节中为了表述方便,将考虑了气缸体容积的模型称为模型1,未考虑气缸体容积的模型称为模型2。模型1及模型2均在AVL BOOST平台中进行仿真计算。仿真模型运行的计算机为64位 Windows 7操作系统,配置为Intel Core i7处理器,主频3.40 GHz,内存8 GB。数值模型的计算步长由软件自动调整,以减少人为干预步长对计算时间的影响。模型1中模型的计算步长为0.057 31°曲轴角,模型2中模型的计算步长为0.058 23°曲轴角。根据仿真结果,所有参数在30个计算循环后达到稳态值。计算30个循环时,模型1的平均计算时间为90.5 s,模型2的平均计算时间为78.3 s,考虑了气缸体的仿真模型单个柴油机循环的计算量多耗时0.4 s,增加15.6%。
选取了主机功率、爆发压力、增压器转速、空冷器出口温度、扫气总管压力、扫气总管温度、排气总管压力、排气总管温度8个参数,以模型1、模型2第30个柴油机循环的计算值作为计算结果与实际测量值对比分析,其结果如图5所示。图中的所有压力值为绝对压力值。从图5的仿真结果可知:模型1计算的结果与实验结果基本一致;模型2计算出来的结果中,扫气温度与实验值差别很大,其他参数的计算结果与实验值均有一定的差别,但是影响较小;模型2中的主机功率、气缸爆发压力比模型1的计算值高;模型2中扫气温度、扫气压力、排气总管温度、排气总管压力、增压器转速等参数的计算值比模型1的计算值低。

图5 模型仿真结果对比Fig.5 Comparison of simulation results of models
为了量化模型各个性能参数的精度及其提高程度,分别定义了最大相对误差(Er)、最大相对误差提高度(Era)、100%负荷时的相对误差提高度(Ere)、最大误差提高量(Ea)这四个参数。设Vm为选取的测量点集合,Vc为相应的计算点值。vc,k为Vc中第k个值,vm,k为Vm中的第k个值。则相对误差ek可表示为
(17)
柴油机模型某一性能参数在各个负荷下的相对误差向量可表示为
E=(e1,e2,e3,…)
(18)
为了方便描述,定义相对误差向量的绝对值运算为
|E|=(|e1|,|e2|,|e3|,…)
(19)
则柴油机模型某一性能参数的最大相对误差的计算公式为
Er=sign(vm-vt)·max(|E|)
(20)
模型2与模型1相比,某一性能参数的最大相对误差提高程度为
Era=sign(e2,i-e1,i)·max(|E2|-|E1|)
(21)
式中:E2表示模型2某一性能参数在各个负荷下的相对误差向量,E1表示模型1某一性能参数在各个负荷下的相对误差向量。100%负荷时,模型2与模型1相比,某一性能参数的相对误差提高程度为
Ere=|e2,r|-|e1,r|
(22)
式中:e2,r表示模型2在100%负荷下的相对误差,e1,r表示模型1在100%负荷下的相对误差。模型2与模型1相比,各个参数的误差提高程度:
Ea=max(|Vc2-Vm|-|Vc1-Vm|)
(23)
根据以上误差指标计算出的模型1、模型2的各个性能参数与实验数据的最大偏差值如表3所示。其中Pw为主机功率,pz,max为气缸爆发压力,nk为增压器转速,Tm为空冷器出口温度,Ts为扫气总管温度,ps为扫气总管压力,Te为废气总管温度,pe为废气总管压力。
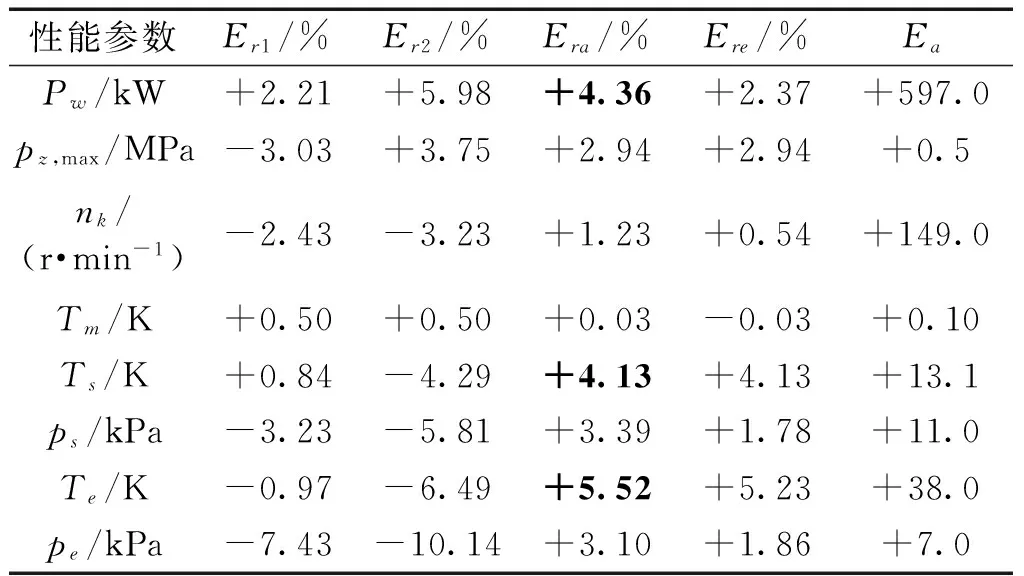
表3 性能参数量化评价指标Table 3 Quantitative evaluations of performance parameters
从表3中分析可知,模型1的最大误差为废气总管压力,值为-7.43%;其次为扫气总管压力,值为-3.23%。模型2的最大误差也是废气总管压力,值为-10.14%;其次为废气总管温度,值为-6.49%。与模型2相比,模型1的精度较高,精度提高程度最高的为废气总管温度,提高5.52%;其次为主机功率,提高4.36%;再次为扫气总管温度,提高4.13%。在100%负荷工况时,模型1的精度比模型2的精度高,提高程度最大的为废气总管温度,提高5.23%;其次为扫气总管温度,提高4.13%。
根据模型1与模型2的对比分析可知,柴油机模型中气缸体模型存在与否对扫气总管温度、排气总管温度、主机功率等参数影响较大。以活塞在上止点为0°曲轴角,根据模型1计算出曲轴角从0°360°,100%负荷时气缸体内工质温度及气缸体与扫气总管之间的质量流量的变化关系,如图6所示。根据仿真结果对上述现象进行定性分析。
从图6可知,活塞从上止点下行时,气缸体容积中的工质在活塞的作用下将逐渐被挤压到扫气总管。同时,由于气缸内壁的温度远高于吸入气缸体中新鲜空气的温度,气缸体中的新鲜空气将受到气缸内壁的加热作用,温度升高。挤压出气缸体的较高温的空气与扫气总管中空气混合,在多缸作用下,扫气总管温度明显升高。随着活塞的下行,扫气口逐渐打开,扫气总管中的低温空气流经气缸体容积与气缸体中的空气混合后进入气缸。在扫气口打开时气缸体中的空气温度达到峰值,与扫气总管中的低温空气混合后,气缸体中的空气温度迅速降低。扫气口打开后,质量流量迅速增加,扫气口关闭后,空气流量迅速下降,质量流量曲线出现一个显著凸峰。随着活塞的上行,扫气口逐渐关闭,空气流量迅速下降。但是活塞上行,气缸体容积随着活塞的上行而变大,扫气总管中仍然有大量新鲜空气继续涌入气缸体容积。这些空气仍然受到气缸内壁的加热作用,由于空气流量较大、空气加热面积仅为气缸下部且温度较低,工质温度整体表现为下降。随着活塞的上行,越过活塞最大速度点后,空气流量降低。同时,气缸上部温度较高、加热面积扩大,气缸体内的工质温度逐渐升高。

图6 气缸体中工质的温度及扫气总管与气缸体之间的质量流量Fig.6 Temperature of working medium in cylinder body and mass flow between intake manifold and cylinder body
考虑了气缸体容积的船用二冲程柴油机模型,整体上表现为进入气缸中的空气温度较高,驻留在气缸中的总空气质量减少、压缩始点温度升高。这将导致压缩终点压力降低、爆压降低、最高燃烧温度升高、气缸排温升高、指示功降低。
5 结论
1)根据热力学原理建立了气缸体子模型并融合到柴油机整机模型中。通过对比分析包含气缸体子模型和未包含气缸体子模型的柴油机整机模型的仿真结果得出,气缸体子模型对排气总管温度、主机功率、扫气总管温度三个参数影响最大,最大提高精度分别为5.52%、4.36%以及4.13%。
2)未考虑气缸体容积子模型的二冲程柴油机模型不能体现气缸体对扫气总管中工质的加热作用以及扫气总管与气缸体之间的质量交换机理。不能体现压缩始点的工质状态与扫气总管中的工质状态的区别。
3)增加了气缸体子模型的二冲程柴油机模型的建模机理结构更加合理。模型的平均单个柴油机循环计算时间从2.61 s增加到3.02 s,单个柴油机循环的计算时间增加0.42 s,增幅为15.6%。
[1] NIKZADFAR K, SHAMEKHI A H. An extended mean value model (EMVM) for control-oriented modeling of diesel engines transient performance and emissions[J]. Fuel, 2015, 154: 275-292.
[2] FINESSO R, SPESSA E. A control-oriented approach to estimate the injected fuel mass on the basis of the measured in-cylinder pressure in multiple injection diesel engines[J]. Energy conversion and management, 2015, 105: 54-70.
[3] SAKELLARIDIS N F, RAPTOTASIOS S I, ANTONOPOULOS A K, et al. Development and validation of a new turbocharger simulation methodology for marine two stroke diesel engine modelling and diagnostic applications[J].Energy, 2015, 91: 952-966.
[4] MURPHY A J, NORMAN A J, PAZOUKI K, et al. Thermodynamic simulation for the investigation of marine diesel engines[J]. Ocean engineering, 2015, 102: 117-128.
[5] MAROTEAUX F, SAAD C. Combined mean value engine model and crank angle resolved in-cylinder modeling with NOx emissions model for real-time diesel engine simulations at high engine speed [J]. Energy, 2015, 88: 515-527.
[6] 韩恺, 吴滔滔, 赵长禄, 等. 基于DOE和神经网络的增压柴油机实时模型建模方法研究[J]. 内燃机工程, 2014, 35(1): 57-62.
HAN Kai, WU Taotao, ZHAO Changlu, et al. Development of real-time capable turbocharged diesel engine model based on DOE and neural network[J]. Chinese internal combustion engine engineering, 2014, 35(1): 57-62.
[7] GRONDIN O, STOBART R, CHAFOUK H, et al. Modelling the compression ignition engine for control: review and future trends[C]//SAE Papers. Detroit, USA, 2004, 2004-01-0423.
[8] DINESCU D C, TAZEROUT M. Mean value modeling of a variable nozzle turbocharger (VNT)[J]. Bucharest scientific bulletion, series D, 2010, 72(1): 109-116.
[9] 周毅.内燃机气缸壁面传热计算中各公式计算结果比较[C]//中国内燃机学会.上海市内燃机学会第六届学术年会论文集.上海,中国, 1998: 76-81.
[10] NIKZADFAR K, SHAMEKHI A H. Investigating the relative contribution of operational parameters on performance and emissions of a common-rail diesel engine using neural network[J]. Fuel, 2014, 125: 116-128.
[11] 郭蕴华,石侠红,杨建国. 船用低速柴油机台架实验及试航管理系统开发[J]. 武汉理工大学学报:交通科学与工程版, 2012, 36(4): 840-843.
GUO Yunhua, SHI Xiahong, YANG Jianguo. Development of shop test and sea trial management system for low-speed marine diesel engines[J]. Journal of Wuhan University of Technology:Transportation science & engineering, 2012, 36(4): 840-843.
本文引用格式:
唐元元, 张均东, 贾宝柱, 等. 气缸体对船舶柴油机模型精度的影响[J]. 哈尔滨工程大学学报, 2017, 38(12): 1836-1843.
TANG Yuanyuan, ZHANG Jundong, JIA Baozhu, et al. The effect of cylinder body on the accuracy of marine diesel engine model[J]. Journal of Harbin Engineering University, 2017, 38(12): 1836-1843.
