不同系泊条件下浮力筒涡激运动模型试验
2018-01-15康庄倪问池张立健
康庄, 倪问池,2, 张立健
(1.哈尔滨工程大学 深海工程技术中心,黑龙江 哈尔滨 150001; 2.加州大学伯克利分校 土木与环境工程学院,美国 加利福尼亚 伯克利 94720)
随着海洋石油产业的不断发展,涡激振动现象正在受到越来越多的关注[1],对于涡激振动的研究也正不断深入,并已取得了不少成果。但在当前,对涡激振动的研究主要集中在立管、海底管道等弹性支撑的大长细比的结构上[2-3],且大多采用数值模拟[4-5]或经验模型的方法[6]。对于泊条件下小长细比,尤其是如浮力筒、海洋平台等质量比为小于0.5的结构的自由涡激运动响应规律的实验研究,当前还没有充足的资料。
模型试验是研究涡激运动响应规律的有效方法。对于小质量比与长细比结构, Williamson对质量比为0.76和0.26的水下系泊圆球进行涡激运动实验研究,发现在较大的约化速度范围内圆球横向最大振幅可达到0.55D左右,且振动频率既不等于固有频率,也不等于静止圆球的漩涡脱落频率[7]。
随后,Williamson等在对低质量比圆柱自由振动模型实验中总结出:如果圆柱质量比小于0.54,则在有限的约化速度下,圆柱的振动响应不会出现下端分支[8]。
Wilde等通过模型实验研究了自由站立式立管的浮筒在系统不同振动模态下的涡激运动响应,发现在一定的来流速度下,浮筒会产生艏摇运动[9]。
本文以质量比为0.422,长细比为7的浮力筒为对象,在不同系缆绳长度和顶端距水面距离的工况下开展了模型试验,并对其运动轨迹、幅值、频率、艏摇特征等进行了对比和研究,得到不同系泊条件下小质量比结构的涡激振动响应规律。
1 模型试验对象及工况
本次浮力筒涡激运动模型试验的场地为哈尔滨工程大学拖曳水池。该水池长108 m,宽7 m,深3.5 m,试验水温为20 ℃。
试验装置的设置如图1所示。浮力筒由一根细绳系泊,细绳一端连接圆柱底部中心,另一端系在沉入水中的铁框中心,细绳的伸缩变形以及旋转阻尼在实验过程中可以忽略不计。铁框通过四根等长绳索固定在拖车上,且与池底保持一定距离。为了增加铁框的稳定性,在铁框中装入较重的压载块,同时,在垂直拖车运行方向(横流向)两边又各系一根细绳,以限制其横流向的位移。

图1 实验装置示意图Fig.1 Schematic diagram of experimental device
浮力筒的运动响应由Qualisys系统捕捉,其原理如下:在圆柱体上安装三个独立的反光球,并使用Qualisys高速摄像机对光球的运动情况进行捕捉,通过光球的运动参数进行处理,得到圆柱体的运动响应。如图1所示,反光球由铁丝架固定并连接在浮力筒顶部中心处。铁丝架与反光球的质量不足50 g,远小于浮力筒的质量,因此其质量可以忽略。在本次试验中,设定采样频率为50 Hz,且保持反光球始终处于水面以上。
本次试验的研究对象为系泊浮力筒模型,浮力筒采用玻璃钢制作,整体呈刚性,重心位于几何中心处。浮力筒的具体尺寸为:外径D=100 mm;长度L=700 mm;自重2.32 kg;排水量5.5 kg;长细比a*=7(a*=L/D)。
为了全面研究各参数对浮力筒涡激运动响应的影响,工况设置时考虑了筒顶部距水面的距离、系缆绳长度以及流速的影响,具体设置如表1。其中,顶部距水面距离与直径比H*取正值代表浮筒顶部在水面以下,0代表浮筒上端和水面平齐,负值代表超出水面。L*为系缆绳长度与直径比,试验中拖车速度由计算机控制,设定范围为0.1~0.3 m/s,速度间隔为0.01 m/s。定义拖车运动方向为顺流向,垂直于拖车运动方向为横向。
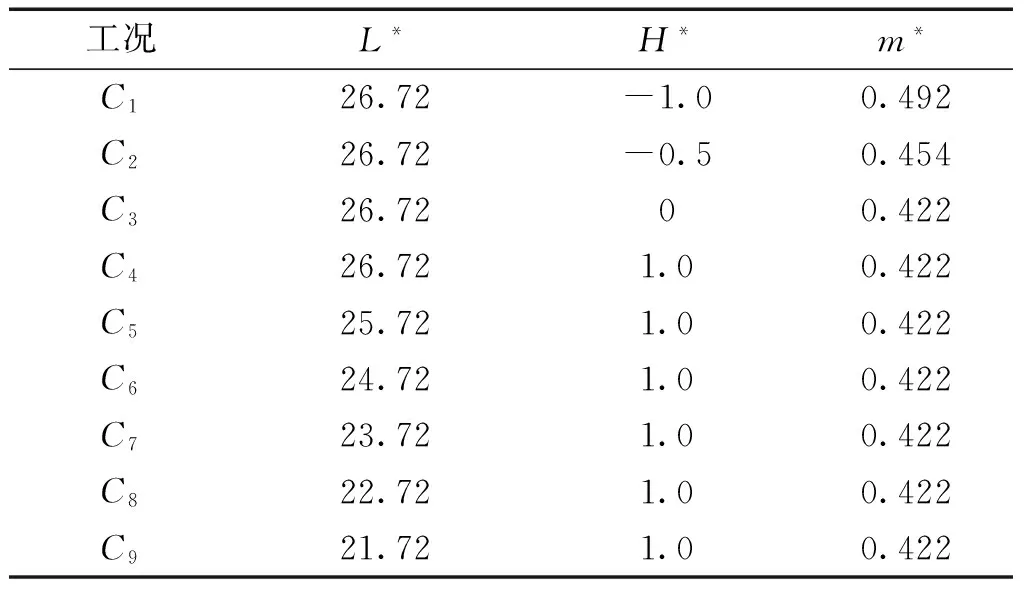
表1 浮力筒的试验工况
2 试验结果分析
2.1 振动固有频率分析
浮力筒的振动固有频率通过测量静水自由衰减试验位移历时曲线上相邻波峰或波谷之间的时间间隔求得。各工况的固有频率计算结果如表2所示。
由表2可得,当浮力筒上端与水面平齐或高出水面时,振动固有频率小于顶端没入水中的工况,且高出水面距离越多,其固有频率越小。当浮力筒顶端没入水中深度不变时,振动固有频率约为0.2 Hz,且随着系泊长度的减小而略微减小。其中,C8工况的频率响应存在异常,这有可能是高频分量的存在影响了实验数据的处理精度所致。
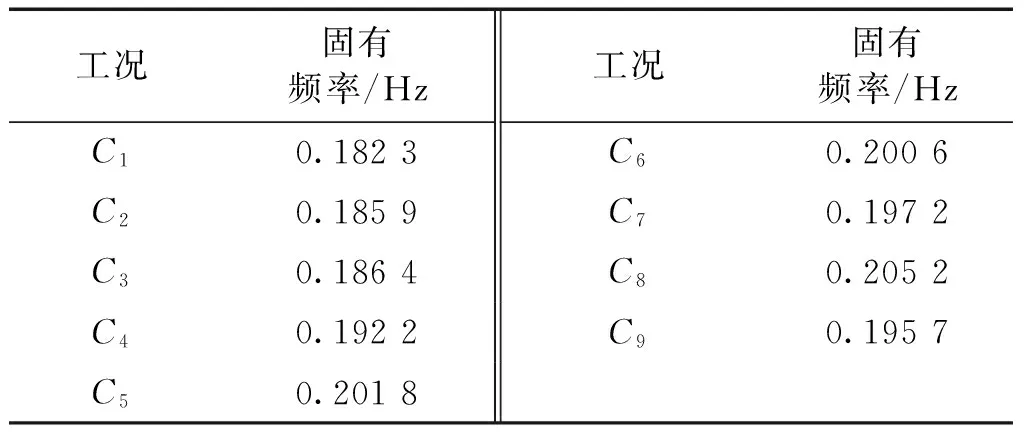
表2 浮力筒振动固有频率Table 2 Natural frequency of the buoyancy can
2.2 浮力筒振幅响应分析
浮力筒在各工况下横向以及纵向均方根振幅响应如图2、3所示。由于各工况约化速度起始值约为5,超过了初始分支的约化速度,试验中浮力筒振幅响应未出现初始分支。
图2 浮力筒各工况横流向运动均方根幅值Fig.2 The cross-flow RMS amplitudes of the buoyancy can in different test conditions
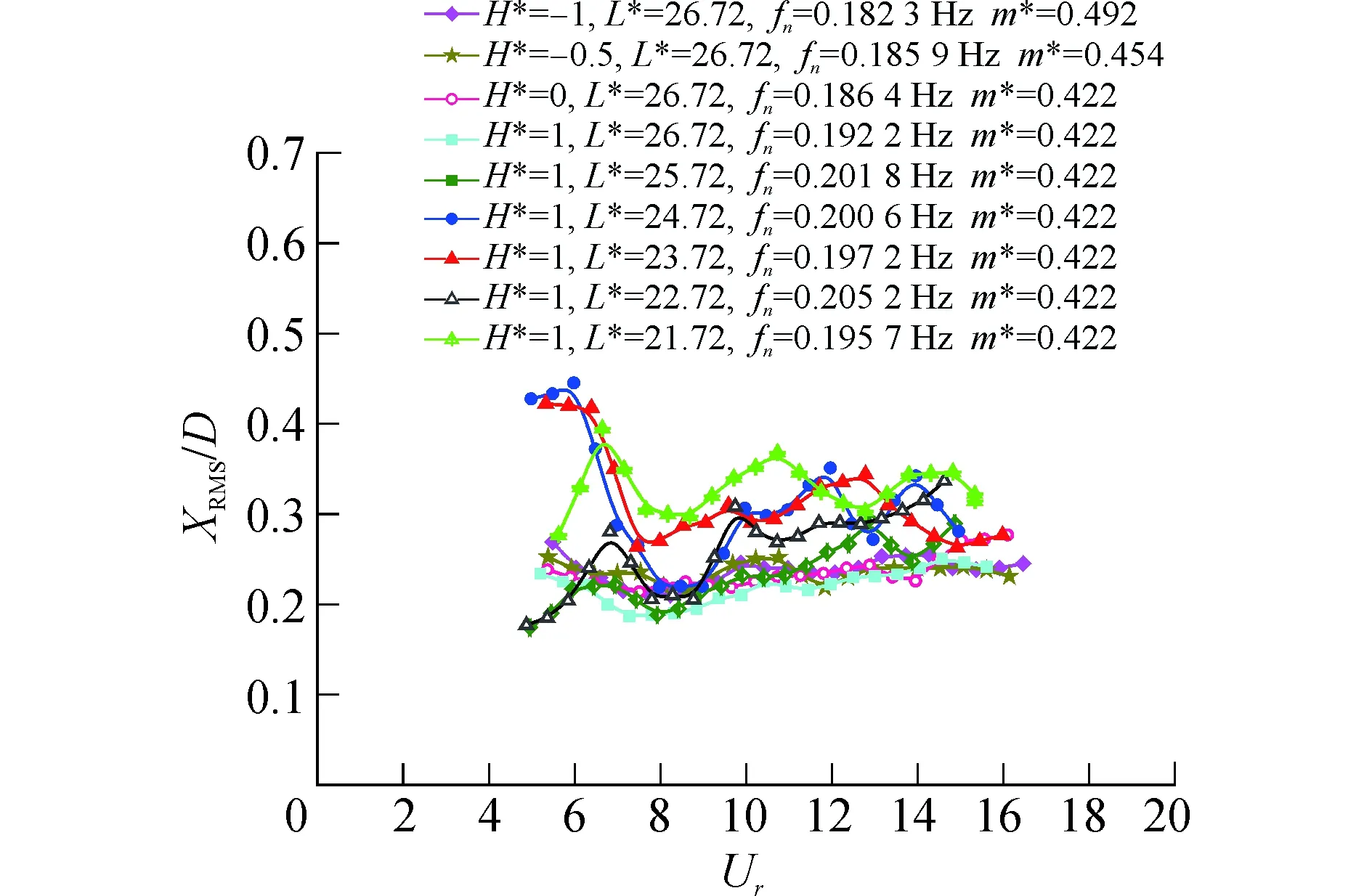
图3 浮力筒各工况顺流向运动均方根幅值Fig.3 The in-line RMS amplitudes of the buoyancy can in different test conditions
由图2可见,浮力筒的横向振幅随约化速度的增加持续增加,且增幅不断减小,最大均方根幅值约为0.9,但在约化速度Ur为7~8附近振幅有短暂下降。具体分析C1~C4工况可以发现,浮力筒顶端露出水面时,横流向运动幅值要小于顶端与水面平齐以及顶端没入水面时的响应,且顶端与水面平齐和顶端没入水面以下时均方根幅值大致相等。对比工况C5~C9的响应可以发现,改变系缆绳长度对浮力筒横流向运动幅值影响规律不明显,L*=24.72时幅值最大。
如图3所示,总体而言,浮力筒的顺流向最大振幅较为杂乱,无明显规律。具体分析各工况的振幅响应可以发现,C1~C4四个工况的顺流向运动均方根幅值随约化速度增大近似保持不变,且幅值大致相等,约为0.23D,可见当L*保持不变,改变浮力筒顶端和水面距离对浮力筒顺流向涡激振动幅值影响不大。分析工况C5~C9可得,保持浮力筒顶端没入水中深度不变时,总体来说,系缆绳长度越小顺流向运动幅值越大,且约化速度介于5~6.5时运动幅值较大,最大均方根幅值达到了约0.45D。
此外,横流向和顺流向运动均未出现下端分支和非共振区,从运动幅值分析认为在整个试验约化速度5~16.5内小直径浮力筒处于“锁定”区。
贾鲁生[10]曾对尺度为Φ11 cm×120 cm圆柱体进行了双自由度涡激振动试验,圆柱体直径与长细比和本文试验中的浮力筒很接近,但其质量比约为2。对圆柱体振幅随约化速度变化的研究中发现当约化速度Ur≈8.5时横流向和顺流向振幅最大,横流向均方根振幅约为0.8,顺流向均方根振幅约等于0.225;且约化速度Ur处于8.45~10.1,振动幅值维持在较高水平。随后振幅随约化速度增大迅速下降,可以观察到明显的下端分支。
通过对比可以发现,浮力筒和双自由度圆柱涡激振动的最大振幅基本相等,但浮力筒在较大的约化速度范围内都能保持在最大运动幅值附近,并未出现非共振区与下端分支。而圆柱最大振幅只在较小的约化速度范围内出现,且有明显的非共振区与下端分支。证明了当质量比较小时,在有限的约化速度下圆柱的振动响应不会出现下端分支。
2.3 浮力筒振动频率及轨迹分析
由于各工况下轨迹与频率响应差异不大,此处以C4工况为例,分析浮力筒振动频率及轨迹的变化规律。需要注意的是,在某些约化速度下,振动频率存在某些低频或高频分量,但所占比重较小,本节中仅分析主要频率。记顺流向、横向振动频率分别为fx与fy,图4为浮力筒横流向无量纲频率、顺流向与横流向振动频率比以及浮力筒运动轨迹随约化速度的变化趋势。
与传统的涡激振动频率响应规律不同,小质量比浮力筒横流向振动频率仅在很小约化速度范围内锁定于其运动固有频率,在其余约化速度下,浮力筒横向振动频率既不等于其固有频率,也不等于静止圆柱绕流漩涡脱落频率,而是在fn~fst,且随约化速度增大呈现出线性增大的趋势,仅在邻近的约化速度范围内存在振动频率相等的情况。该现象与Govardhan等[8]的圆球涡激运动振幅响应规律类似。此外,在约化速度变化范围内,顺流向运动频率约为横流向运动频率的2倍,除了在约化速度较小时略有波动。相应地,浮力筒的运动轨迹也呈明显的“8字形”,并且顺流向运动的平衡位置向来流方向下游偏移,且偏移量随试验流速增大而增大。
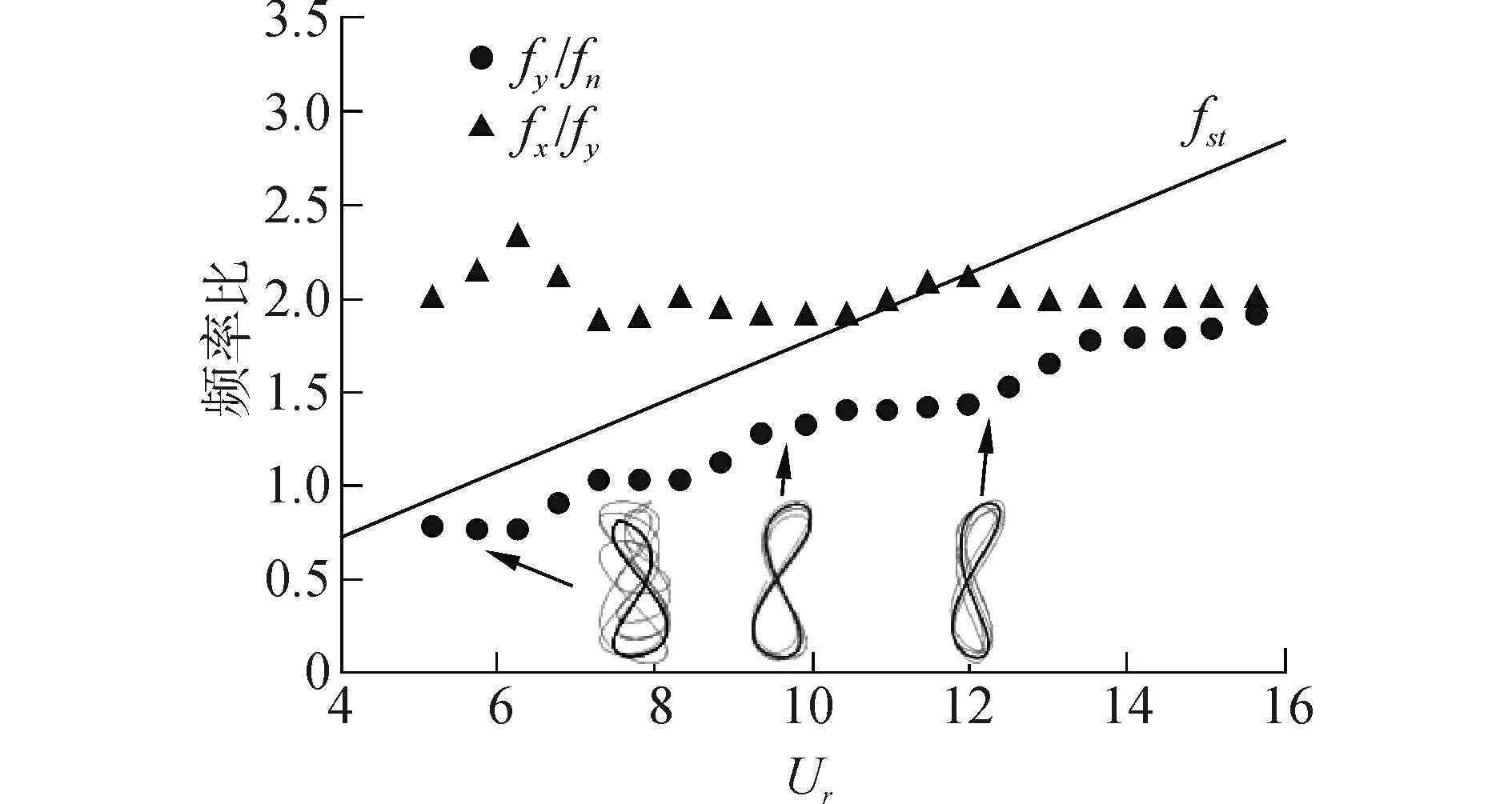
图4 浮力筒涡激振动频率及轨迹Fig.4 The frequency and trajectory of vortex induced vibration of the buoyancy can
2.4 浮力筒艏摇特性分析
Rijken等指出,伴随着涡激振动的漩涡交替泄落,在圆柱体两侧会产生压力差[11]。在压力差的作用下,圆柱体不仅会发生横向运动,而且该压力差还会在水平面内产生一定的扭转力矩作用,使得圆柱体发生艏摇运动。在本文的浮力筒涡激振动实验中也观察到了艏摇现象。
与振动频率类似,在某些约化速度下,艏摇运动频率也存在某些低频或高频分量,但所占比重较小,因此本文仅对其主频率进行分析。为了探究艏摇运动和横向运动的激励力来源是否相同,本文将C4工况下艏摇运动与横向振动频率进行了对比,结果如图5所示。同时,将典型的艏摇与横向振动频域分析结果也显现在图5中。
由图5可见,当约化速度较小时,艏摇运动比较杂乱,其中有一个较大的频率分量与横向振动主频率相等。同时,横向振动也有一个较为明显的频率分量与艏摇运动的主频率相等。当约化速度大于6.5后,艏摇运动与横向振动都趋于稳定,仅有一个主要频率,且两者频率相等。由此可以证明,艏摇运动和横向运动具有相同的激励力来源,即艏摇运动是涡激振动过程中交替脱落的漩涡,由圆柱体两侧产生的压力差造成的。
各工况下,浮力筒艏摇运动的均方根幅值如图6所示。总体而言,当流速为0.1 m/s时,艏摇运动均方根幅值最大,达到了3.3 rad左右。当约化速度在5.3~7.0时,艏摇运动幅值随约化速度增大而迅速减小。当约化速度大于7以后,艏摇运动幅值基本保持不变但有随约化速度增大而缓慢减小的趋势,并且基本稳定在0.5 rad左右。
对比各工况的艏摇响应可以发现,改变系泊线长度和浮力筒顶端与水面距离(分为与水面平齐、露出水面和水面以下)等对艏摇运动幅值大小和变化趋势影响不大。

图5 艏摇运动与横向振动频率对比曲线Fig.5 Comparison of yaw motion and lateral vibration frequency
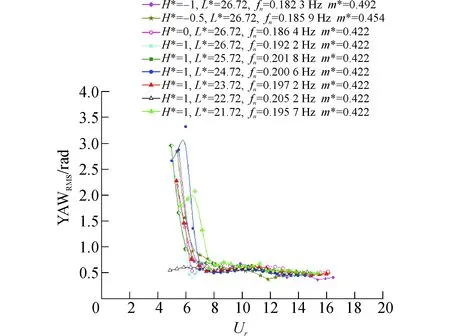
图6 浮力筒艏摇均方根幅值Fig.6 Yaw RMS amplitude of the buoyancy can
3 结论
1)浮力筒顶端露出水面时,横流向运动幅值要小于顶端与水面平齐以及顶端没入水面时的响应。而系缆绳长度对浮力筒横流向运动幅值影响不大。
2)浮力筒顶端和水面距离对浮力筒顺流向涡激振动幅值影响不大。而系缆绳长度越小顺流向运动幅值越大。
3)当质量比较小时,在有限的约化速度下圆柱的振动响应不会出现下端分支。
4)小质量比浮力筒横流向振动频率仅在很小约化速度范围内锁定于其运动固有频率,在其余约化速度下,浮力筒横向振动频率既不等于其固有频率,也不等于静止圆柱绕流漩涡脱落频率,而是在fn~fst,且随约化速度增大呈现出线性增大的趋势。且顺流向运动频率约为横流向运动频率的2倍,轨迹呈明显的“8字形”。
5)当约化速度较小时,艏摇运动比较杂乱,其中有一个较大的频率分量与横向振动主频率相等。同时,横向振动也有一个较为明显的频率分量与艏摇运动的主频率相等。当约化速度大于6.5以后,艏摇运动与横向振动都趋于稳定,仅有一个主要频率,且两者频率相等。艏摇运动是由浮力筒两侧漩涡交替脱落形成的压力差引起的。
6)系泊线长度和浮力筒顶端与水面距离对艏摇响应影响不大。
[1] KANG Z, NI W, MA G, et al. A model test investigation on vortex-induced motions of a buoyancy can[J]. Marine structures, 2017, 53: 86-104.
[2] KANG Z, JIA L. An experiment study of a cylinder′s two degree of freedom VIV trajectories[J]. Ocean engineering, 2013, 70: 129-140.
[3] JAUVTIS N, WILLIAMSON C H K. The effect of two degrees of freedom on vortex-induced vibration at low mass and damping[J]. Journal of fluid mechanics, 2004, 509(509): 23-62.
[4] XU J, ZHU R. Numerical simulation of VIV for an elastic mounted on the spring supports with low mass-ratio[J]. Journal of marine sciences & application, 2009, 8(3): 237-245.
[5] KANG Z, NI W, SUN L. A numerical investigation on capturing the maximum transverse amplitude in vortex induced vibration for low mass ratio[J]. Marine structures, 2017, 52: 94-107.
[6] 唐友刚, 青兆熹, 张杰,等. 深海立管涡激振动预报模型及影响因素[J]. 哈尔滨工程大学学报, 2017, 38(3): 338-343.
TANG Yougang, QING Zhaoxi, ZHANG Jie, et al. Prediction model and influence factors on vortex-induced vibration of deepwater risers[J]. Journal of Harbin Engineering University, 2017, 38(3): 338-343.
[7] GOVARDHAN R, WILLIAMSON C H K. Vortex-induced vibrations of a sphere[J]. Journal of fluid mechanics, 2005, 531(531): 11-47.
[8] GOVARDHAN R, WILLIAMSON C H K. Modes of vortex formation and frequency response for a freely vibrating cylinder[J]. J Fluid Mech, 420: 85-130.
[9] WILDE J D. Model tests on the vortex induced motions of the air can of a free standing riser system in current [R] Netherlands: Maritime Research Institute, 2007.
[10] 贾鲁生.多边界条件下双自由度圆柱体自激振动试验研究[D].哈尔滨:哈尔滨工程大学, 2012.
JIA Lusheng. Investigation on self-excited vibration of 2-D of cylinder under multi boundary conditions[D]. Harbin: Harbin Engineering University, 2012.
[11] RIJKEN O, LEVERETTE S. Experimental study into vortex induced motion response of semi submersibles with square columns[C]//Proceedings of the 27th International Conference on Offshore Mechanics and Arctic Engineering. Estoril, Portugal, 2008: 263-276.
本文引用格式:
康庄, 倪问池, 张立健. 不同系泊条件下浮力筒涡激运动模型试验[J]. 哈尔滨工程大学学报, 2017, 38(12): 1823-1827.
KANG Zhuang, NI Wenchi, ZHANG Lijian. An experimental investigation on vortex-induced motion of buoyancy can under various mooring conditions[J]. Journal of Harbin Engineering University, 2017, 38(12): 1823-1827.
