尾坐式无人机过渡模式纵向解耦控制

张迪洲, 陈自力, 胡永江

(陆军工程大学石家庄校区无人机工程系, 河北 石家庄 050003)

0 引 言

尾坐式无人机是一种垂直起降固定翼无人机,其既能像旋翼无人机一样垂直起降、空中悬停,又能以固定翼无人机的方式快速水平飞行,因此在军用和民用市场都有着非常广阔的应用前景[1-2]。与其他种类的垂直起降固定翼无人机相比,尾坐式无人机不需要复杂的倾转机械结构,其通过大角度俯仰机动和拉力控制实现垂直飞行模式和水平飞行模式之间的转换。然而,在飞行模式过渡过程中,无人机的飞行速度、俯仰角、攻角和气动参数等都会发生较大的变化,受此影响无人机的飞行高度很难得到稳定的控制和保持。针对尾坐式无人机过渡模式纵向协调控制问题,国内外已经进行了一些相关的研究[3-5]。

尾坐式无人机过渡过程的控制问题主要包括两个方面,一是控制策略的设计,即安排过渡过程中俯仰角指令、飞行速度指令和飞行高度指令等;二是姿态角回路在过渡过程中的稳定和控制。本文主要针对第一个问题进行研究,其姿态控制回路采用文献[5]中的比例微分积分(proportion-integration-differentiation， PID)控制技术结合增益调度方法进行控制。

对于尾坐式无人机过渡过程控制策略的设计,许多学者将其描述成一个优化问题。文献[6]采用序列二次规划(sequential quadratic programming, SQP)优化方法,在保持高度不变的约束下,以时间最短为目标函数,设计了尾坐式无人机过渡过程的俯仰角、拉力控制策略。文献[7]研究了尾坐式无人机过渡过程最短时间优化和最小能量消耗问题。此外,文献[8]研究了尾坐式无人机过渡过程最小时间优化问题,文献[9]研究了过渡过程最小高度变化优化问题。但以上文献中采用的都是离线计算、开环控制的方法,需要根据数学模型提前计算出时间序列下的俯仰角指令和飞行速度指令,所以其控制性能很大程度上依赖无人机数学模型的精确性,而且离线计算方法自适应性较差,对干扰较为敏感。

尾坐式无人机过渡模式飞行控制问题,目标是在保持高度不发生变化的前提下,实现俯仰角和飞行速度在不同飞行模式下的转变,其本质上可以归结为飞行速度和飞行高度的纵向解耦控制问题。现代飞行控制中对纵向通道常采用基于单输入单输出(single input single output, SISO)的控制策略,利用俯仰姿态回路控制飞行高度,利用油门控制飞行速度。由于俯仰角、高度和速度控制有着不利的耦合作用,因此设计起来较为复杂[10]。文献[11-13]提出的总能量控制系统(total energy control system, TECS),采用了多输入多输出的控制策略,从动能和势能的角度出发,通过控制飞机总能量的变化与分配,直接构造解耦环节,实现对纵向飞行高度与飞行速度的解耦控制。本文基于TECS解耦控制思想对尾坐式无人机过渡过程的在线飞行控制策略进行了设计,同时拓展了TECS方法在大攻角飞行运动下的应用。

1 过渡过程特性分析

本文研究的尾坐式无人机采用无机身飞翼式布局,如图1所示。机翼前缘并列装配两个无刷电机,驱动一对正反桨,平衡产生的反扭矩。机翼后缘装配一对升降副翼,通过舵机进行控制。在飞行过程中,通过调节电机的转速(同步和差速)和升降副翼的偏转(同向和反向)控制无人机的姿态、位置和速度。

图1 尾坐式无人机Fig.1 Tail-sitter unmanned aerial vehicle

假设本文研究的尾坐式无人机为刚体,且质量分布均匀,忽略地球曲率,取地面坐标系O-XgYgZg为惯性坐标系,建立尾坐式无人机的运动学模型为[14]

(1)

(2)

在机体坐标系O-XbYbZb下对无人机的受力情况进行分解,可得

(3)

式中,T为无人机总拉力;L为升力;D为阻力;α为无人机的攻角。

尾坐式无人机在飞行过程中通过调节俯仰角和飞行速度实现垂直飞行模式和水平飞行模式之间的转换,主要依据俯仰角和飞行速度的数值判断无人机所处的飞行模式[15]。在过渡过程的飞行控制中,希望在改变无人机俯仰角和飞行速度的同时,尽量减少无人机飞行高度的变化。

然而,由式(2)和式(3)可知,在飞行模式过渡过程中,无人机俯仰角和飞行速度的改变会引起飞行高度和攻角等发生相应变化,并且无人机的飞行速度、高度和俯仰角等存在耦合关系[16],而无人机纵向运动的可控制量只有电机的转速和升降副翼的偏转角,因此,要实现尾坐式无人机过渡过程纵向运动的协调控制,尽量减少过渡过程中无人机飞行高度的变化,需要深入分析无人机过渡过程中飞行速度、高度、俯仰角、攻角、升力、阻力和拉力等的变化规律和相互关系。

为了分析尾坐式无人机过渡过程各飞行状态的运动规律,采用计算流体力学[17](computational fluid dynamics, CFD)方法对尾坐式无人机过渡模式下的气动特性进行了仿真计算。在定直平飞条件下,分别计算从0°到90°攻角下,无人机的飞行速度、所需拉重比、升力系数和阻力系数等,计算结果如图2所示。部分攻角下的压力分布云图如图3所示。定直平飞条件下,尾坐式无人机的所需拉重比和飞行速度随攻角的变化情况如图2所示。以垂直飞行模式向水平飞行模式过渡为例,当无人机的攻角从90°减小至47°过程中,随着攻角的减小,无人机产生的升力逐渐增大,但此时受到的阻力较大,产生的升力较小,所以无人机的所需拉重比缓慢减小;当攻角从47°减小至10°时,无人机机翼上产生的升力开始明显增加,且迎风面积进一步减小,受到的阻力减小,故无人机的所需拉重比快速减小;当攻角从10°继续减小时,随着攻角的减小,升力系数大幅减小,为了满足定直平飞条件,无人机的飞行速度需要大幅增加,受到的阻力也随之增大,所以无人机的所需拉重比又迅速增大,以克服来流的阻力。尾坐式无人机由垂直飞行模式向水平飞行模式的过渡过程中,随着攻角的减小,飞行速度不断增大,过程中会出现一个所需拉重比最小的攻角,由图2可知,此时无人机的攻角为10°,飞行速度为12 m/s。基于分析,在垂直飞行模式和水平飞行模式下(航迹角为0°),无人机的俯仰角等于攻角,因此在尾坐式无人机的过渡过程中,设定垂直飞行模式的稳态为:θ=90°,V=0 m/s;设定水平飞行模式的稳态为:θ=10°,V=12 m/s。

图2 过渡过程的气动系数、空速和所需拉重比Fig.2 Aerodynamic coefficients, airspeed and neededpull-weight ratio during transition

图3 无人机部分攻角下的压力分布云图Fig.3 Pressure distributions pictures of the UAV atseveral typical attack angles

由仿真计算结果可知,尾坐式无人机在飞行模式过渡过程中,无人机的气动参数、飞行速度和拉力等都发生了较大的变化,且变化规律呈非线性特征,难以用精确的数学模型进行描述。为了尽量减小无人机过渡模式的飞行高度变化,目前常用的方法是对无人机俯仰角和飞行速度按照离线计算的配平状态匹配关系进行控制[6-8],然而,气动特性仿真计算过程中对无人机的模型进行了适当简化,其计算结果与真实数据存在一定的偏差[18],而如果进行风洞实验获取较为精确的气动参数,则所需的工作量较大,且费用昂贵。按照离线数据进行匹配控制的另外一个缺点是当无人机受到干扰导致偏离预设期望轨迹时,后续的自适应能力较差,往往会引起较大偏差[19]。因此,本文将总能量控制理论引入到尾坐式无人机过渡过程的飞行速度、高度和俯仰角的协调控制中,采用在线控制策略,使无人机在过渡过程中飞行高度变化最小。

2 总能量解耦控制方法

总能量控制方法的核心是对纵向航迹角和切向加速度的解耦控制,因此,在气流坐标系O-XaYaZa下建立尾坐式无人机的纵向运动模型为

(4)

式中,V为飞行速度;γ为轨迹倾斜角;Iyy为转动惯量;M为俯仰力矩。

由式(4)得

(5)

在惯性坐标系下建立尾坐式无人机的纵向运动模型为

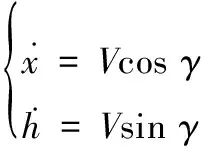
(6)

无人机的总能量ET等于无人机动能和势能的总和，即

(7)

对式(7)求微分,得

(8)

将式(6)代入式(8),可得

(9)

mg与V的乘积可视为比例系数,因此,定义无人机的总能量变化率为

(10)

TECS利用总能量的变化与转移特性将无人机的长周期质点运动和短周期姿态运动有效地统一起来。由式(10)可知,无人机在飞行过程中,总能量的变化主要通过拉力T进行调节。文献[20-22]中设计的TECS都有3个假设条件:阻力D不发生变化,轨迹倾斜角sinγ=γ,攻角α=0。对于民航飞机而言,其纵向机动较小,速度变化缓慢,在短周期运动中,可以认为阻力基本不变,且飞行过程中轨迹角、攻角较小。然而,尾坐式无人机在过渡过程中阻力、轨迹角和攻角都会发生较大的变化,因此在TECS设计过程中,需要综合考虑阻力、轨迹角和攻角的变化。

定义

(11)

将式(11)代入式(10),可得

(12)

δT的增量为

(13)

式中,Ve=Vc-V；(sinγ)e=sinγc-sinγ；下标e表示偏差量；下标c表示期望值(下文同)。由式(12)和式(13)可知

(14)

式中,∝表示“正比于”。因此,可通过调节δT的大小来控制无人机总能量的变化,设计无人机总能量变化的控制律为

(15)

为了防止比例通道在传递函数上产生不希望的零点[18],在式(15)的比例控制部分使用总能量变化率反馈量,即

(16)

由式(11)可得

ΔTcosα=ΔD+mgΔδT

(17)

cosα可视作比例系数,因此设计无人机总拉力的控制律为

(18)

无人机的阻力D=0.5ρV2SCD,其中阻力系数受许多因素影响,由于所研究的尾坐式无人机属于低空、慢速、小型无人机,因此该无人机的阻力系数CD主要受攻角的影响。

阻力D的增量为

(19)

式中，CD通过第一节中生成的无人机气动数据库查表获得,因此无法直接对其求导。求CD对α的偏导数为[23]

(20)

由α=θ-γ,且轨迹角期望值γc=0,可得

Δα=αc-α=θc-θ+γ

(21)

式中,θc通过总能量分配率控制通道获得。

TECS中的总能量的转移主要通过控制俯仰角实现动能和势能之间的相互转换,为了保证动能和势能具有同等的控制优先级,用俯仰姿态回路控制总能量的分配率,定义为势能与动能的变化率之差为

(22)

同式(15)和式(16)的方法,设计无人机总能量分配率的控制律为

(23)

(24)

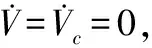
(25)

可得

(26)

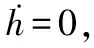
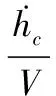
(27)

由于γc=0,当无人机到达稳态时h=hc,可以实现对无人机飞行高度的无差控制。

最终,设计的TECS核心算法如图4所示。

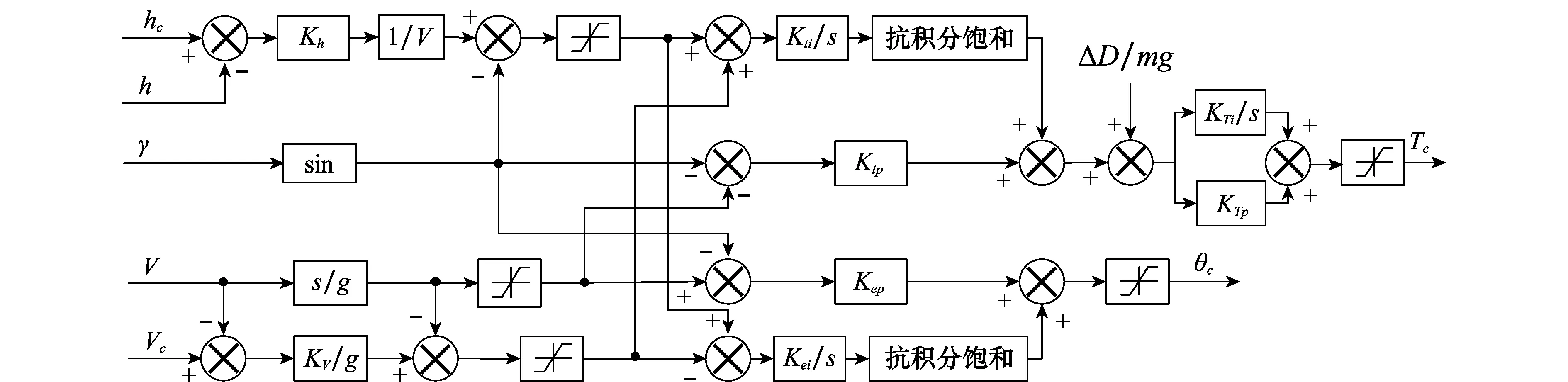
图4 TECS核心算法结构框图Fig.4 Core architecture of TECS

当尾坐式无人机在垂直飞行模式和水平飞行模式之间过渡时,主要改变无人机飞行速度和俯仰角的控制指令,其中飞行速度控制指令直接作为TECS输入信号Vc,俯仰角控制指令θc由TECS的总能量分配通道生成,飞行高度指令hc设定为无人机过渡开始前的高度,即期望过渡过程飞行高度不发生变化。垂直飞行模式向水平飞行模式过渡时设置Vc=12 m/s,水平飞行模式向垂直飞行模式过渡时设置Vc=0 m/s,由于TECS控制要求Δh=0,俯仰角控制指令由TECS系统根据高度和飞行速度的偏差信号计算获得,因此可认为,生成的俯仰角控制指令与无人机的飞行速度可使无人机满足定直平飞条件。

无人机的拉力是有限制的,并且大于等于零,为了防止总能量控制的积分通道出现积分饱和问题,影响控制效果,在积分通道上加入拉力抗积分饱和比例系数，即

同理,过渡过程无人机的俯仰角变化范围为[0°,90°],为了防止总能量分配的积分通道出现积分饱和问题,加入俯仰角抗积分饱和比例系数

抗积分饱和环节的作用是,当TECS的输出达到拉力或俯仰角的上、下限值后,切除积分作用,这样当偏差减小时,控制器的输出能够更快脱离拉力或俯仰角的上限或下限值,从而保证控制器具有良好的性能。

为了防止无人机过渡过程由于速度指令的突变造成偏差量过大引起系统的振荡,对控制器的加速度、轨迹角等通道均设置了限幅环节。

3 仿 真

以上介绍的尾坐式无人机为例,对无人机飞行模式过渡过程中的飞行速度/飞行高度解耦控制进行仿真飞行实验,验证本文设计的TECS解耦控制方法的可行性。仿真中,考虑作动器约束,升降副翼偏转范围为-30°～30°,总拉力调节范围为0～15 N。本文无人机质量m=0.78 kg,Iyy=0.005 1 kg·m2,重力加速度g=9.8 N/kg。控制器参数为:Kh=0.7,KV=0.7,Ktp=1.2,Kti=23,Kep=1.2,Kei=2.6,KTp=2.1,KTi=0.2。仿真初始条件为:无人机处于垂直悬停状态,初始高度h0=100 m,初始速度V0=0 m/s,初始俯仰角θ0=90°,初始拉力T0=mg。仿真开始时,无人机处于垂直飞行模式,设置速度指令Vc=0 m/s,高度指令在整个仿真过程中保持定值hc=100 m。当仿真时间t=100 s时,无人机由垂直飞行模式向水平飞行模式转换,设置速度指令Vc=12 m/s;当仿真时间t=200 s时,无人机由水平飞行模式向垂直飞行模式转换,设置速度指令Vc=0 m/s。为了对比验证设计的TECS解耦方法的性能,采用传统的飞行速度/高度双通道SISO控制方法进行相同条件下的仿真,SISO方法在垂直飞行模式下由油门控制飞行高度,俯仰角控制指令θc=90°,在过渡模式和水平飞行模式下由油门控制飞行速度,升降副翼(俯仰角回路)控制飞行高度,仿真结果如图5所示。

图5 尾坐式无人机过渡过程仿真结果Fig.5 Simulation results of the tail-sitter UAV during the transition

由仿真结果图5(a)和图5(b)可知,在尾坐式无人机飞行模式的过渡过程中,采用TECS解耦控制方法的控制效果明显优于SISO方法。两种方法在速度控制回路都有比较好的控制效果,但SISO方法在无人机过渡过程中高度误差较大(最大误差5 m),而TECS解耦控制方法在两种过渡模式中高度误差均在1 m以内,可见TECS解耦控制方法可以使尾坐式无人机在飞行模式过渡过程中保持高度和速度的解耦控制,使无人机处于定直平飞条件下。

由图5(b)和图5(c)可知,由于TECS解耦控制方法存在高度无差控制环节,因此在飞行速度指令发生突变时,速度响应与SISO方法相比较为缓慢,生成的俯仰角控制指令更为平缓,这更加有利于俯仰角姿态控制回路的跟踪控制,使尾坐式无人机在过渡过程中保持稳定的控制性能。

由图5(e)和图5(f)可知,采用TECS解耦控制方法在飞行模式过渡过程中的升降副翼偏转角和油门控制量更小,说明TECS方法更节能、更高效。

4 结 论

本文针对尾坐式无人机飞行模式过渡过程纵向速度、高度的解耦控制问题,采用总能量控制理论设计了过渡过程纵向解耦控制策略:

(1) 将总能量控制理论引入到尾坐式无人机的过渡过程飞行控制中,解决了过渡过程飞行高度、速度的解耦控制问题;

(2) 设计了非线性形式的总能量控制系统,拓展了总能量控制系统在考虑阻力变化和大攻角运动下的应用,且算法简单,计算量小,易于工程实现。

仿真结果表明,采用TECS解耦控制方法使尾坐式无人机在过渡过程中取得良好的速度、高度解耦控制效果,过渡过程高度基本保持不变(最大误差小于1 m)。下一步将对基于TECS解耦控制方法的过渡模式最短时间控制和最小能耗控制进行研究,并对其实际飞行实验效果进行验证。

[1] WANG X H, CHEN Z Q, YUAN Z Z. Modeling and control of an agile tail-sitter aircraft[J]. Journal of the Franklin Institute, 2015, 352(12): 5437-5472.

[2] KITA K, KONNO A, UCHIYAMA M. Hovering control of a tail-sitter VTOL aerial robot[J]. Journal of Robotics and Mechatronics, 2009, 21(2): 277-283.

[3] NALDI R, MARCONI L. Robust control of transition maneuvers for a class of V/STOL aircraft[J].Automatica,2013,49(6): 1693-1704.

[4] KITA K, KONNO A, UCHIYAMA M. Transition between level flight and hovering of a tail-sitter vertical takeoff and landing aerial robot[J].Advanced Robotics,2010,24(5/6):763-781.

[5] JUNG Y, SHIM D H. Development and application of controller for transition flight of tail-sitter UAV[J]. Journal of Intelligent and Robotic Systems, 2012, 65(1): 137-152.

[6] OOSEDO A, ABIKO S, KONNO A, et al. Optimal transition from hovering to level-flight of a quadrotor tail-sitter UAV[J]. Autonomous Robots, 2017, 41(5): 1143-1159.

[7] NALDI R, MARCONI L. Optimal transition maneuvers for a class of V/STOL aircraft[J].Automatica,2011,47(5):870-879.

[8] STONE R H, CLARKE G. Optimization of transition manoeuvres for a tail-sitter unmanned air vehicle (UAV)[C]∥Proc.of the Australian International Aerospace Congress, 2001:1-14.

[9] KUBO D, SUZUKI S. Tail-sitter vertical takeoff and landing unmanned aerial vehicle: transitional flight analysis[J]. Journal of Aircraft, 2008, 45(1): 292-297.

[10] 吴树范,蔡维黎,沈勇璋,等.飞机总能量控制系统的研究I——原理分析与系统设计[J].航空学报,1993,14(7):A355-A361.

WU S F, CAI W L, SHEN Y Z, et al. Studies on the total energy control system of aircraft I: principle analysis and system design[J].Acta Aeronautica et Astronautica Sinica,1993,14(7): 355-361.

[11] LAMBREGTS A. Functional integration of vertical flight path and speed control using energy principles[C]∥Proc.of the Annual NASA Aircraft Controls Workshop, 1983: 389-409.

[12] LAMBREGTS A. Integrated system design for flight and propulsion control using total energy principles: AIAA-1983-2561[R]. Reston: AIAA, 1983.

[13] LAMBREGTS A. Vertical flight path and speed control autopilot design using total energy principles: AIAA-1983-2239[R]. Reston: AIAA, 1983.

[14] 吴森堂, 费玉华. 飞行控制系统[M]. 北京: 北京航空航天大学出版社, 2005: 58-59.

WU S T, FEI Y H. Flight control system[M]. Beijing: Beijing University of Aeronautics and Astronautics Press， 2005: 58-59.

[15] STONE R H, ANDERSON P, HUTCHISON C, et al. Flight testing of the t-wing tail-sitter unmanned air vehicle[J]. Journal of Aircraft, 2008, 45(2): 673-685.

[16] FORSHAW J L, LAPPAS V J. Transitional control architecture, methodology, and robustness for a twin helicopter rotor tailsitter[C]∥Proc.of the AIAA Guidance, Navigation, and Control Conference, 2012: 1-16.

[17] KIM C, CHUNG J. Aerodynamic analysis of tilt-rotor unmanned aerial vehicle with computational fluid dynamics[J]. Journal of Mechanical Science and Technology, 2006, 20(4): 561-568.

[18] STONE R H. Aerodynamic modeling of the wing-propeller interaction for a tail-sitter unmanned air vehicle[J]. Journal of Aircraft, 2008,45(1): 198-209.

[19] GARCIA O, CASTILLO P, WONG K C, et al. Attitude stabilization with real-time experiments of a tail-sitter aircraft in horizontal flight[J].Journal of Intelligent and Robotic Systems,2012,65(1): 123-136.

[20] 吴树范,沈勇璋,郭锁风.飞机总能量控制系统的研究II——非线性控制律综合与仿真[J].航空学报,1994,15(9):1043-1050.

WU S F, SHEN Y Z, GUO S F. Studies on total energy control systems of aircraft II: nonlinear control law integration and aimulation[J]. Acta Aeronautica et Astronautica Sinica, 1994, 15(9): 1043-1050.

[21] 张庆振, 安锦文. 一种基于飞机总能量控制飞行速度/航迹的解耦控制系统设计控制新方法[J]. 航空学报, 2004,125(14):389-392.

ZHANG Q Z, AN J W. A new method for designing decoupling controller of flight speed/flight path based on total energy control[J]. Acta Aeronautica et Astronautica Sinica, 2004, 125(14): 389-392.

[22] FALEIRO L P, LAMBREGTS A A. Analysis and tuning of a ’total energy control system’ control law using eigenstructure assignment[J].Aerospace Science and Technology,1999,3(3):127-140.

[23] KURDJUKOV A P, NATCHINKINA G N, SHEVTCHENKO A M. Energy approach to flight control[C]∥Proc.of the AIAA Guidance, Navigation, and Control Conference, 1998: 543-553.