基于插值-拟合-迁移学习算法的机载设备故障概率预测

顾涛勇, 郭建胜, 李正欣, 王 健, 王腾蛟

(空军工程大学装备管理与安全工程学院, 陕西 西安 710051)

0 引 言

机载设备故障概率预测是航空维修保障的一个重要问题。对故障概率预测问题的研究,存在以下两种主要的求解思路,即基于模型的故障概率预测与基于数据驱动的故障概率预测[1]。相对于基于模型的故障概率预测需要获取研究对象的精确的故障概率模型,基于数据驱动的预测方法应用更为灵活,因此受到了广泛的关注[2]。文献[3-5]对常用算法在故障预测中的运用进行了分析,但是机载设备故障原因复杂、不确定性强、样本不足等问题导致这些方法很难发挥其优势。

在数据驱动的故障概率预测方法中,插值与拟合是最为高效的方法。而迁移学习[6],或称归纳迁移,是机器学习中的一个重要研究问题,其目标是将某个领域或任务上学习到的知识或模式应用到不同但相关的领域或问题中[7]。迁移学习试图实现人通过类比进行学习的能力,可以很好地解决样本不足的问题。

通过分析机载设备故障数据,发现机载设备的故障概率不仅仅和飞行时次相关,不同的工作环境也会对故障概率造成影响。单独对各个工作环境的数据分析会引起样本不足的问题,基于样本特征的迁移学习[8]可以解决这一问题。本文在插值、拟合与迁移学习的基础上,提出了一种针对于不同工作环境的机载设备故障概率预测算法。算法将插值、拟合与迁移学习通过自适应权重进行线性组合,在提升数据利用效率的同时规避迁移学习所带来风险。

1 问题描述

在研究机载设备故障概率预测问题时,由于设备价格昂贵,通过实验建立精确的设备故障概率模型是不现实的。那么历史故障数据就成了预测其故障概率的主要依据。为了区分工作环境,即对不同的工作环境给出不同的故障概率分布函数,数据量往往不充足并且不平衡。在样本较少的情况下,插值、拟合方法都很难精确地描述故障概率,选择类似数据进行迁移学习是有效的数据补充手段;而在样本充足的情况下,迁移学习会稀释其数据特征,造成负迁移现象。什么时候选择迁移,选择哪些数据进行迁移,如何迁移,是决定学习效果的3个关键问题[6]。针对以上3个问题,本文提出了自适应权重的插值-拟合-迁移学习(interpolation-fitting-transfer learning, IFT)算法。

2 IFT算法

IFT算法模仿了人对数据归纳、类比的能力,充分利用所掌握的信息,以减小数据量不充足、不平衡所带来的预测误差。该算法对插值、拟合、迁移学习赋予一定的权重进行线性组合。算法的主要公式为

fr(x,t)=

(1)

式中,fr(x,t)表示工作环境为x,飞行时次为t的设备预测故障概率;α·IP(x,t)是故障频率分布的插值;β·FIT(x,t)是根据分布函数的拟合;∑[θ(x,x′)·IP(x′,t)]是对其他工作环境故障数据的迁移学习,其中x′∈X-x。α、β、θ分别为插值、拟合与迁移学习权重。由于α、β、θ齐次,且次数为0,所以在工作环境x数据量不为0的情况下,默认α=1;当工作环境取值为x的数据量为0时,默认α=0。

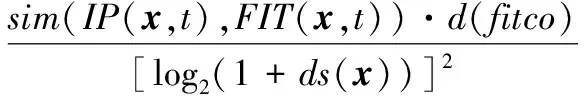
(2)

式中,sim(IP(x,t),FIT(x,t))是拟合与插值的分布相似度;d(fitco)为拟合函数的参数数量;ds(x)为工作环境x的样本数量。

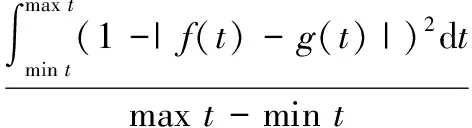
(3)

式中,分布相似度sim(f(t),g(t))表示分布f(t)与g(t)的相似程度。由于故障预测是为了备件与维修工作,所以采用的相似度量与备件、维修风险度量相关。

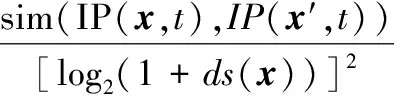
(4)

式中,x′∈X-x,diff(x,x′)表示工作环境x与x′中取值不同的维,例如x1=(机型1,气候条件1),x2=(机型1,气候条件2),diff(x1,x2)={气候条件}。

ie(Xd)=-∑p(Xd)·log2(p(Xd))

(5)

式中,ie(Xd)表示维向量Xd的信息熵。

对应于前文中所提及的迁移学习关键问题[6],IFT算法遵循以下两个准则:①当前样本数据越少,插值和拟合方法越难以趋近真实的概率分布,则迁移学习权重越高;②迁移学习数据与当前数据的相似度越高,则其权重越大。所以，迁移学习权重θ(x,x′)与分布相似度(根据式(3)计算)、信息熵(根据式(5)计算)和数据量相关。工作环境x数据量为0时,默认sim(IP(x),IP(x′))-1。

3 算法理论分析

本节将分析插值、拟合与迁移学习在预测结果中所占的比例,讨论算法的复杂度和简化方法,以验证算法的合理性与可行性。

3.1 IFT比例

工作环境x的数据量为0时,α=β=0,有

fr(x,t)=∑[θ(x,x′)·IP(x′,t)]/∑θ(x,x′)

θ(x,x′)=[log2(1+ds(x′))]2/ie(diff(x,x′))

预测只来自于迁移学习,迁移学习权重取决于数据量和信息熵。工作环境x的数据量为+∞时,α=1,β=0,θ(x,x′)=0,fr(x,t)=IP(x,t)预测只来自于插值。

通常情况下,数据量介于以上两种极端情况之间。为了直观地显示IFT比例,假设各个工作环境相互独立并且均匀分布,平均每个变量的可取值数量都为5,默认拟合度为1。

在这样的条件下,IFT比例的变化趋势如图1所示。图1中数据量是关于2的对数,可以发现插值比例随着数据量的增大而增大,拟合与迁移学习则相反。

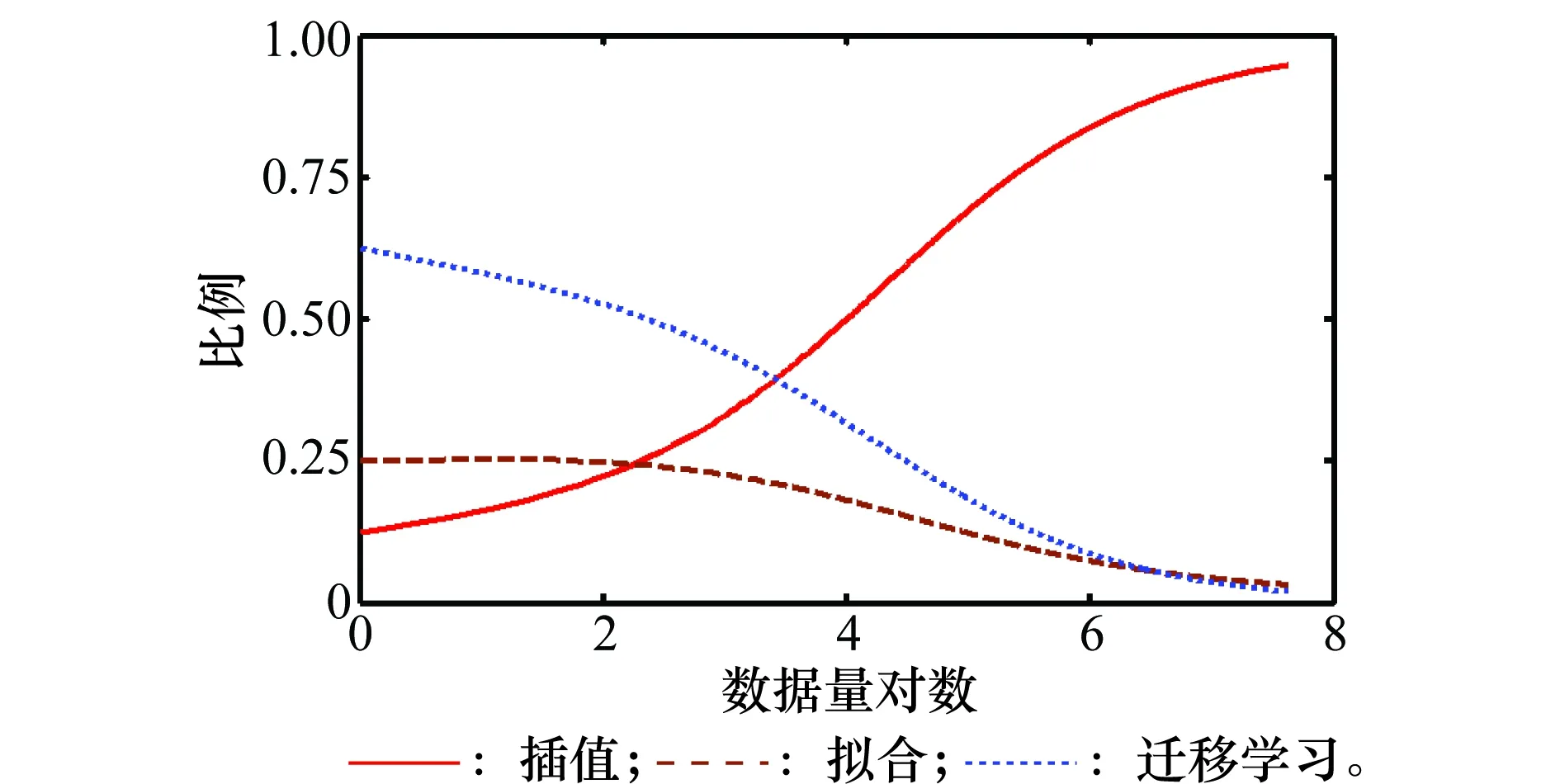
图1 IFT的比例变化Fig.1 Change of IFT’s proportions

3.2 算法复杂度

为了验证算法的可行性,需要对算法的时间复杂度进行分析。假设工作环境x的维数为m,各维的取值数量为n,各个维度相互独立,并且数据量均匀分布,数据总量为D,那么对应于某个工作环境的数据量为d=D/nm。

对于初次学习,采用线性插值,插值复杂度为O(dlog2d),插值次数为nm,总复杂度为O(nm·dlog2d)=O(Dlog2d);最小二乘法拟合指数分布,单项拟合数据量为d,拟合复杂度与精度有一定的关系,可以认为是O(kd),其中k是与指数函数计算精度有关的参数,拟合次数为nm,总复杂度为O(kD)。关于拟合权重与迁移学习项权重的计算,拟合权重β的计算复杂度为O(lD),其中l是与指数函数计算精度有关的参数,拟合权重计算次数为nm,拟合权重计算总复杂度为O(lD)。迁移学习项权重θ(x,x′)的计算复杂度为O(2d),迁移项权重计算次数为n2m,迁移项权重计算总复杂度为O(n2m·D)。所以，初次学习的总复杂度的数量级为O(n2m·D)。

3.3 简化方法

对于增量学习,每增加一条数据,由于有迁移学习的存在,算法需要重新计算1次插值频率、1次拟合频率、1次拟合权重和nm次迁移项权重,总复杂度为O(nm·D)。在原有数据量D的基础上新增数据量D′,复杂度为O(nm·D′2+nm·D·D′),在数据量大、维数多的情况下会导致组合爆炸,所以考虑对其进行简化。根据算法特征,有3种简化方法:

(1) 新增数据积累到一定量后进行一次重计算;

(2) 限制迁移学习范围;

(3) 对工作环境维度进行剪枝。

4 仿真实例

4.1 数据集

仿真实例选择某一段时间某型号机载设备的故障数据。数据格式为(搭载机型,气候条件,飞行时次),其中搭载机型4种,气候条件6种,数据量为249。一般认为该设备故障概率服从Weibull分布,之前采用的预测主要方法也是Weibull拟合。

如图2所示,对于全局故障数据(不区分工作环境),其拟合程度相当高。但是不同机型和气候条件的故障概率分布存在一定差异,如图3和图4所示。针对各工作环境,采用同一个插值或是拟合函数不能区分工作环境所带来的差异;而对每一种工作环境单独进行插值或是拟合则会由于数据量不足而产生误差。

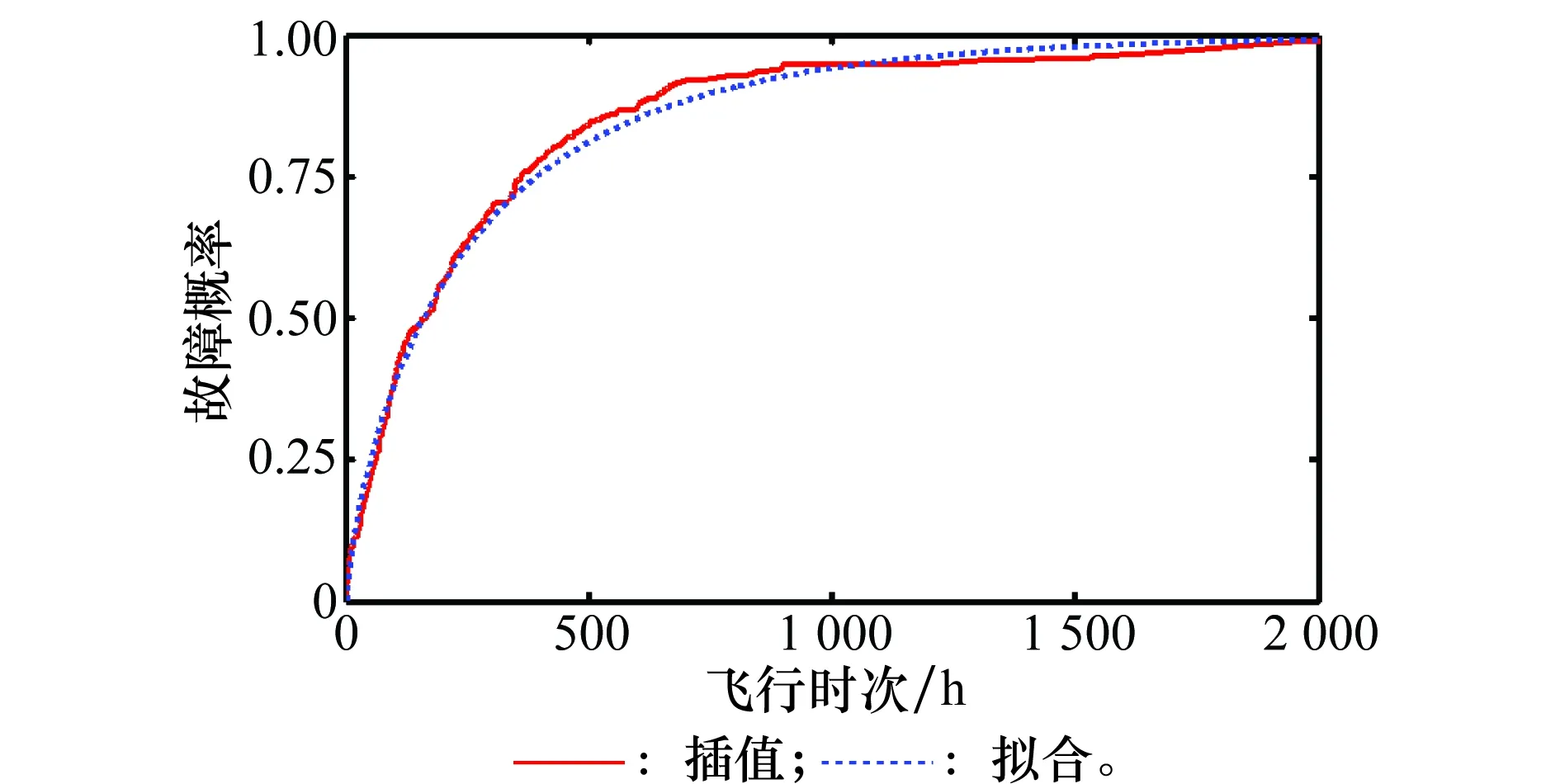
图2 故障频率与Weibull拟合Fig.2 Fault frequency and Weibull fitting

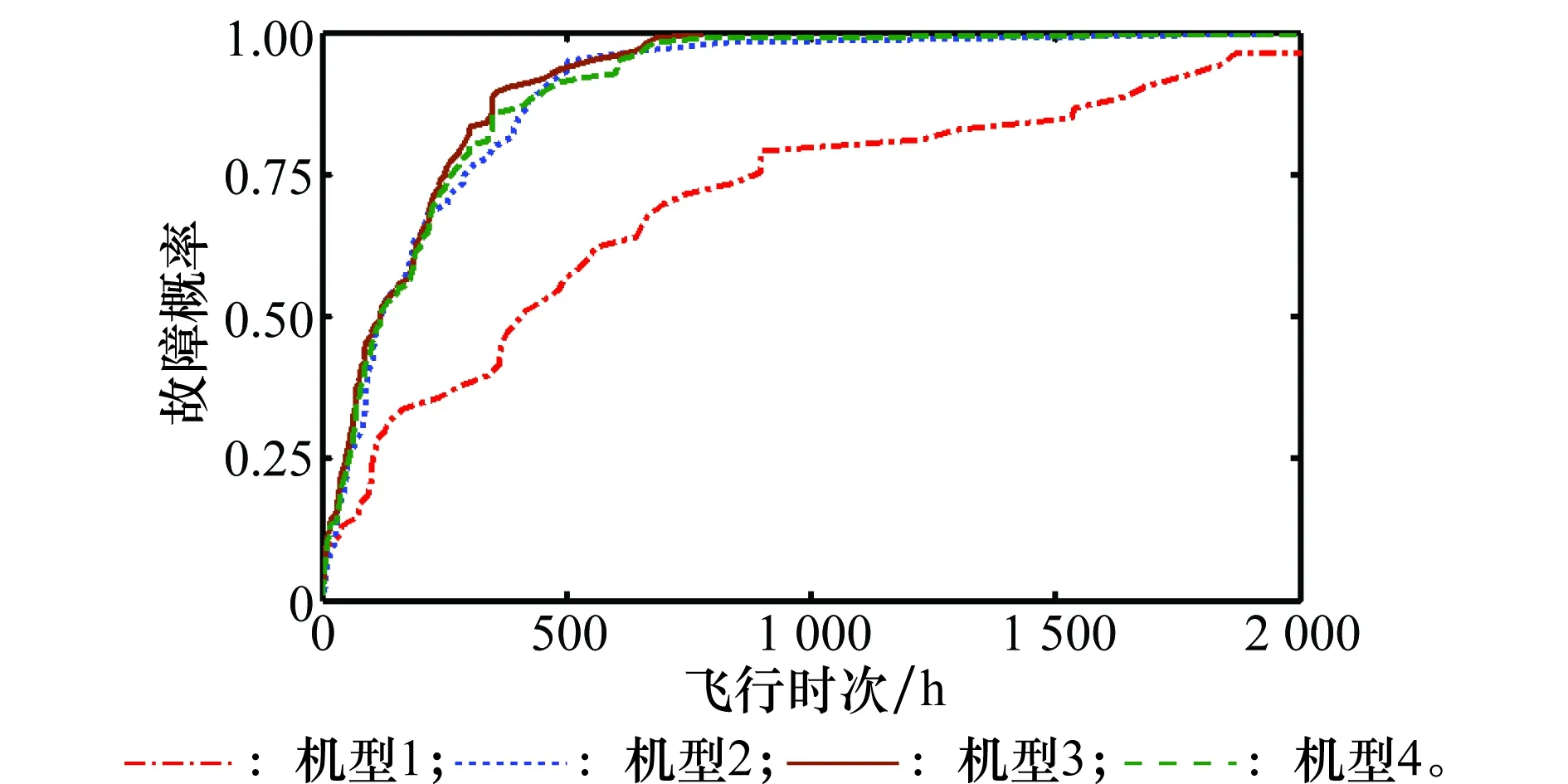
图3 各机型故障频率Fig.3 Fault frequency distinguished by aircraft type

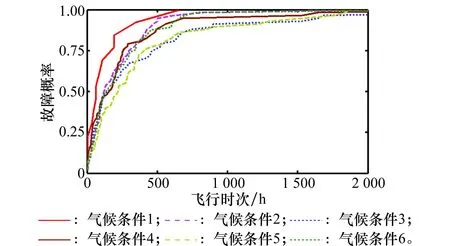
图4 各气候条件故障频率Fig.4 Fault frequency distinguished by climate condition

由于真实的故障概率分布未知,需要保留一定量的数据作为校验集,以预测概率和校验集频率的分布相似度来衡量算法效果。为了模拟真实情况,数据按输入时间顺序来划分,前156条作为训练集D,后93条数据作为校验集D′。

4.2 算法步骤

步骤1根据式(5)计算工作环境差异信息熵值。

步骤2计算频率插值、分布拟合。实例选择线型插值和最小二乘Weibull分布拟合[9-10]。

步骤3计算拟合权重β、迁移学习项权重θ与IFT比例。其中积分步长大小取1,由于分布函数单调递增,函数值取积分区间的中点值。

步骤4计算预测概率分布。根据所得的α、β、θ,以及式(1)来计算各个工作环境下的故障概率分布。

4.3 结果对比

对于全局故障数据(不区分工作环境)的概率分布,对线型插值、Weibull分布拟合以及IFT 3种方法进行比较(见表1)。对于各工作环境故障概率分布,对线型插值(区分工作环境)、Weibull分布拟合(区分工作环境)、全局线型插值(不区分工作环境)、全局Weibull分布拟合(不区分工作环境)以及IFT 5种方法进行比较(见表2)。

表1 全局预测准确度(不区分工作环境)比较

如表1所示,对于全局故障数据而言,不论是插值、拟合还是IFT方法,都有很高的准确率。如表2和表3所示,在区分工作环境的情况下,IFT方法表现出了一定的优势(其中数据量为0的工作环境不进行检验,不在表格中出现)。尤其对于数据量较少的工作环境,迁移学习能提高预测结果的稳定性,避免数据量少而导致的极大误差(如表2中的工作环境12、14)。在实例中,工作环境仅仅考虑了机型和气候条件,向量维数较少,IFT方法的优势不明显,但随着工作环境维数的增加,IFT方法的优势会逐渐增大。

表2 各工作环境预测准确度比较

表3 各工作环境平均预测准确度比较

5 结 论

本文分析了IFT算法的复杂度,通过实例展现了其优势,论证了IFT方法是一种可行并且有效的机载设备故障概率预测方法。IFT算法的主要优势在于:

(1) 算法体现了不同工作环境对机载设备故障概率预测的影响;

(2) 算法根据数据量和数据特征自适应调整各部分比例,规避了数据贫化所带来的预测风险,也减少了负迁移现象。

为了能满足大多数机载设备的故障概率预测需求,仍存在一些问题需要解决:

(1) 除了工作环境(枚举型),数据中还存在其他影响设备故障概率造成的因素,例如对于可修复件,有历史故障次数(离散型)、历史总飞行时次(连续型);

(2) 数据的内容、结构不同;

(3) 数据中存在大量的缺失值。

对于这些问题,需要适用范围更广的相似度度量和数据特征迁移学习方法,这将在下一步工作中进行研究。

[1] LUO J H, NAMBURU M, PATTIPATI K, et al. Model-based prognostic techniques[C]∥Proc.of the Autotestcon IEEE Systems Readiness Technology Conference, 2003: 330-340.

[2] 张磊, 李行善, 于劲松, 等. 基于关联向量机回归的故障预测算法[J]. 系统工程与电子技术, 2010, 32(7): 1540-1543.

ZHANG L, LI X S, YU J S, et al. Fault prognostic algorithm based on relevance vector machine regression[J]. Systems Engineering and Electronics, 2010, 32(7): 1540-1543.

[3] ZHANG C L, HE Y G, YUAN L F, et al. A novel approach for analog circuit fault prognostics based on improved RVM[J]. Journal of Electronic Testing Theory & Applications, 2014, 30(3): 343-356.

[4] EKER O F, CAMCI F. State-based prognostics with state duration information[J]. Quality and Reliability Engineering International, 2013, 29: 465-476.

[5] XIA F, ZHANG H, LONG J Q, et al. Fault diagnosis of turbine unit equipment based on data fusion and RBF neural network[J]. Lecture Notes in Computer Science, 2011, 7002(2): 74-81.

[6] PAN S J, YANG Q. A survey on transfer learning[J]. IEEE Trans.on Knowledge & Data Engineering,2010,22(10):1345-1359.

[7] 龙明盛. 迁移学习问题与方法研究[D]. 北京: 清华大学, 2015.

LONG M S. Transfer learning: problems and methods[D]. Beijing: Tsinghua University, 2015.

[8] 杨士准. 基于样本和特征的迁移学习方法及应用[D]. 长沙: 国防科学技术大学, 2016.

YANG S Z. Instance-based and feature-based transfer learning approaches with their applications[D]. Changsha: National University of Defense Technology, 2016.

[9] LU H L, CHEN C H, WU J W, et al. A note on weighted least-squares estimation of the shape parameter of the Weibull distribution[J].Quality & Reliability Engineering International, 2004, 20(6): 579-586.

[10] 魏星. 基于多组样本和顺序统计量的威布尔分布参数置信区间的估计[D]. 上海: 上海交通大学, 2016.

WEI X. The confidence intervals for the Weibull parameters based on multi-sample and order statistic[D]. Shanghai: Shanghai Jiaotong University, 2016.