从“误解”走向“悟解”——基于关系视角的教学误解的成因分析和转化策略

赵庆林

（扬州市梅岭小学，江苏 扬州 225002）

一、一个好的教育概念：误解

（一）教学中的误解

教与学是课堂中最重要的一组关系，误解是教与学关系中经常发生的事情。在《现代汉语词典》中，“误解”有两层含义，作为动词是指“理解得不正确”，作为名词是指“不正确的理解”。教学中的误解，当然也包含这两层意思。作为动词，它主要指基于教与学背后的主体关系而发生的行为，往往表现在三个方面：第一，教师误解学生，第二，学生误解教师，第三，学生误解学生。作为名词，它主要指基于教与学背后的实际内容而产生的结果，往往表现在认识主体和认识对象之间所建立起的不正确的联系。对于课堂来说，误解意味着一种“敞开的封闭”；对于教与学来说意味着一种“理解的缝隙”。前者使课堂看上去是敞开的、开放的，但实则是封闭的；后者使教与学看上去是走向相互理解的，但实则是走向隔阂的。

教学是建立一种认识上的合情合理的关系，虽然误解隐藏着为理解而做的努力，但毕竟还是破坏了这种关系。因而，课堂教学就是消除误解的过程，也就是认识上“祛魅”，然后建立正确关系的过程。

（二）误解的教育价值

我们说误解是一个好的教育概念，正是因为它具有丰富的教育价值。

1.误解也是一种理解

误解本质上也是一种理解，它是教师与学生、学生与学生之间基于学习活动而产生的不同的认识结果，携带着这些不同的认识，教师与学生、学生与学生之间相互产生了理解上的偏差，但是误解本质上是一种理解，只不过这种理解是个人化的、不正确的，是需要相互澄清、相互走向、相互打通的。因而误解不等于错误，至少在主观上它更多是由于无意识而引起的，而在客观上它是由于诸多认识关系网中某种“断裂”造成的。误解也是一种理解，是对认识主体包含的学习主动性的承认，也是对理解的复杂性的发现。

2.误解也是一种资源

作为一种过程，误解的产生有其背后深层次原因，而对这些原因的发现与剖析，为教学增加了多元的视角和有益的素材。这是教学宝贵的资源。多元的视角使我们在教学过程中面对学生的问题和错误变得更加“冷静”和“客观”，使我们有了相互理解的现实需要和促进相互理解的可能；而有益的素材指学生口头上、行动上所表现出的理解偏差，是学生澄清认识最好的起点和阶梯。误解也是一种资源，它不仅包含多元的视角，更是现实的素材。

3.误解也是一种教育

教学总是在寻找澄明的地带。对于学习来说，由于认识的器官——人的大脑和认识的对象——知识世界之间存在永恒的距离，因而，误解的产生和消除误解的过程都是暂时的，寻找澄明的认识地带永远是一个未完成的任务，而这也正是教育存在的价值和意义。对于学生来说，没有误解就没有认识上的“华丽转身”；对于教师来说，没有误解就没有教学的“深刻领悟”。误解也是一种教育，是从外部世界引发内部思考的教育，是理解自我走向理解他人的教育，也是教育存在价值和意义的证据。

二、误解产生的原因

误解产生的原因有很多，但普遍认为是事物在建立联系的过程中由于认识的“断裂”造成的，这种认识的“断裂”是客观存在的，也是学习者轻易不能察觉的。发现和理解这种“断裂”是修复认识的前提。

（一）“儿童视角”的误用

在低年级计算教学中，如计算“21-9”，教师在解释“为什么需要从十位上‘借’1个10”时，往往会这样说：“你们不能从较小的数中减去较大的数。”很显然，“不能从较小的数中减去较大的数”是一个错误的数学语句。尽管低年级学生还不能理解如何从较小的数中减去较大的数，但这并不意味着在数学上不能从较小的数中减去较大的数。[1]当然，我们也清醒地认识到，教师做出这样的判断和表达，在很大程度上是因为站在儿童的视角上去看问题，而并非是自己真的不懂。在学生开始认识数的时候，学生就从数的大小比较中建立了对数的直观感知，“不能从较小的数中减去较大的数”的背后有着学生丰富的生活经验的支撑，但如果站在学生长久的学习目标来说，一个错误观念的植入和一个正确观念的植入，谁又会使学生受益呢？教师站在学生的视角看问题是没有错的，但是学生毕竟需要教师的引领，因此，教师的观察和理解绝不能假借所谓的“儿童视角”，而止步于现象的层面。

（二）“知识权威”的影响

在课堂上，知识权威主要分为两类：一类是学生使用的教材，它们是“知识载体”而具有无声的影响力；另一类是教师以及那些学习成绩优异的学生。马立平博士举过这样的案例，计算“53-6”时，所有的美国教师都是将53拆成40和13进行计算，而有些中国教师超越了，他们指出这个运算法则不是进行减法的唯一正确的途径。[2]无独有偶，一次听“两位数加减一位数”的口算复习，教师重视了知识纵向的连贯，通过分类对所学的计算进行整理，先分为加法和减法，再进一步细分为进位加法和不进位加法以及退位减法和不退位减法，但在退位减法和进位加法的复习中，我们只看到标准方法，而非标准方法则几乎没有出现，以退位减法来说，标准方法是高位退一，与原先低位值上的数组合起来，然后再减。这让我们产生疑问，是学生都接受了标准方法？还是学生受制于知识权威？如果学生都接受了标准方法也无可厚非，但是如果学生受制于知识权威，则使听课者以及上课者都会产生错觉，以为学生的思维发展是顺畅整齐的。在教学中，标准方法往往是一种最优的选择，而非标准方法也有其独特的作用，只有在相互比较中，才“可以彻底地揭示出过程背后的概念”。“知识权威”不仅使我们常常误以为学生的学习过程就是如此，更重要的是使我们失去了揭示更为深刻概念的可能。

（三）“学科结构”的模糊

学科的基本结构就是指该学科的基本概念、基本原理和基本规律及其相互联系。学科基本结构的教学价值在于：一是有利于对知识的理解；二是可以更好地记忆学科知识；三是有利于知识、技能的“迁移”；四是能够缩短知识层次间的距离。[3]就数学学科来说，以小学“数的认识”为例，教师不仅要整体上把握整数、小数、分数之间的相互关系，也要在细节上深刻理解它们的内涵。有这样一个案例：请根据条形图（如图1）写出你看到的分数。

图1

（四）“先有概念”的制约

毫无疑问，学习者都是带着先有概念来到教室的。随着时间的推移，这些附着在经验之上的先有概念逐渐累积，最终形成学习者的思维结构。这样的思维结构具有顽固性的特征，同时它们也具有接纳任何事物成为自身一部分的强大能力。因而，才有人认为学习是具有革命性的活动。在“分数的意义”教学中，学生建立单位“1”概念的过程伴随着“先有概念”所产生的各种各样的误解。教师通过一个物体、一个计量单位、一个整体抽象出用自然数“1”表示，但是，学生真的那么容易就理解了单位“1”吗？学生心中真的没有任何疑问了吗？为什么不用单位“2”或其他的数来表示？随后，在引入数轴表示分数的时候，学生把单位“1”与数轴上的“1”混淆在了一起。有的学生能够正确写出0到1之间的分数，是因为他们把0到1之间的部分看作单位“1”，而1到2之间的分数则容易写错，学生只需要认识到1到2之间的部分也可以看作单位“1”，以此类推，3到4，5到6等都可以看作单位“1”，但是，在学生那里，对“1”的认识早已与具体的物和量联系在一起，想要抛开具体事物以及量的特征到达抽象的层面需要突破“先有概念”的制约。“先有概念”的制约提醒教师，在教学过程中，已有经验和概念不仅是学习者发展的基础，还有可能是学习者发展的障碍，它“增加”了误解的合理成分，从而使误解更具有欺骗性。

（五）“重要他人”的缺失

客观上讲，如果教学中的任何行为和结果都经过学习者思维确证的话，教学中的误解发生的可能性会大大降低。最为常见的一个现象是，当教师在课堂教学中发生了一个比较明显的错误，并不是所有学生都能够发现，也并不是所有学生都能够积极主动地指出来。当学生在课堂学习中产生错误的时候，往往会出现两种现象：一种是引起其他学生强烈地“反弹”，但是这种“反弹”有可能是对错误的反应，也有可能是对正确的反应；另一种则是漠不关心，往往出于学生的“不知情”。在“认识小数”的教学中，教师安排学生“在长方形中精准地表示出0.3元”这样一个任务，结果如图2。

出人意料的是，当教师问：“观察以上作品，哪些是骨子里一样的？”大部分学生对图2表示怀疑，显然学生产生了误解，无论是“反弹”的，还是沉默的，同样处于“不知情”的状态。面对这样的现象，教师只能不断引导学生与学生之间开展对话、回应、质疑与讨论，实际上是引导学生与学生之间建立相互支持的学习力量，从而让彼此成为学习过程中的“重要他人”。“重要他人”的缺失不仅关闭了课堂中对话、质疑的窗口，也使学习者失去重要支持而变得孤独。

三、误解的转化：从“误”到“悟”

误解产生于关系中，也必定能够从关系中化解。误解产生于相互中，也必定需要彼此的相互理解。误解的教育价值在于它能够变成转化教师理念和行为的力量。既然是转化，首先需要建立在原有“误”的基础上，其次需要一个现在“悟”的过程。借用文艺理论中“讽刺之道，直诰易尽，婉道无穷”的内蕴，误解转化之道也可用“直诰易尽，婉道无穷”来表达。因而，误解的转化应从“误”到“悟”。

（一）转化的关键是教师

正如弗朗索瓦·多尔托说：“每一个认真听取孩子答案的人都是具有革命性思想的人。”[5]在传统的教学文化背景下，教师占据着交流的主动权，无论是教师与学生之间，还是学生与学生之间，都需要教师围绕教学误解进行点拨、引导和化解。在教学误解产生原因的分析中，不难发现很大程度都与教师相关联。无论是教师对数学学科结构的认识，还是对儿童学习数学现实的理解，都对教学误解的认识和转化起着关键的作用。如果教师疏于对整个教学过程的观察，也缺少对学生先有概念的掌握，那么，首先教师难以发现误解，其次难以找准转化的起点。因而，误解的转化关键是教师。

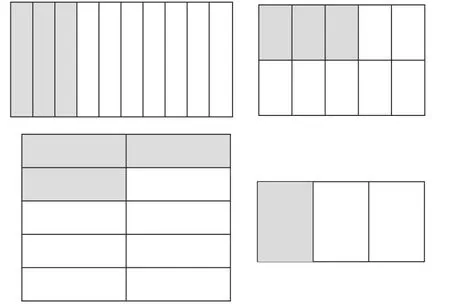
图2

（二）转化的主体是学生

“当教学被当作一种简单的知识传递时，它便不能引发学习，甚至还会阻碍学习。”[6]之所以如此，表面上是因为“教不是学”这样一个简单的道理，本质上是因为学生作为学习主体的不可替代性。虽然教师是教学误解转化的关键，但是教师不能替代学生经历转化的过程。无论哪种原因导致的误解，最终都需要学生自己去“推翻”原来的认识或做法，并在此基础上经由理解的“刷新”重新建立学习的行为。因而，误解的转化主体是学生。

（三）转化的基础是情感

事实上，感情、愿望以及潜在的激情在学习行为中具有战略性的地位。因而，“情感—情绪”维度不应再被遮蔽，或被看作纯粹的“限制因素”。[7]引发误解产生的因素在很大程度上与学生的情感联系在一起，而固有的经验和概念更是与学生的情感密不可分，因而，误解的转化离不开情感的参与，而作为学习重要的构成部分，情感是一切学习活动的源泉，它不仅是学习活动的内在组成部分，更是评价学生学习能力的重要指标。无论是对学习具有的限制作用，还是对学习具有的激发能力，都在表明它是教学中误解转化的基础。

（四）转化的材料是经验

教学中的误解不是空穴来风，误解的产生与人的经验有深度关联，无论是教师对学生的误解，还是学生之间的误解，都借助经验的方式描述或反思，因而，在很大程度上可以说经验产生了误解，而误解又以不同人的不同经验在教学时空中交错呈现。经验分为外部经验和内部经验，外部经验源于感觉器官的“知觉”，内部经验源于内在反思。[8]转化过程依托外部经验和内部经验完成，最终使“看到的”和“想到的”达成一致。

（五）转化的机制是心理

从“误”到“悟”的过程，是由“言”到“心”，由外向内的转变。表面是行为表现的不同，背后是心理变化的差异。当误解产生，教师如果只是单方面解决，表面化处理，只关注学习者外部行为的调整，而忽视其内在学习心理的变化，那么，这样的转化过程将不利于学习者建立真正的理解，也并非是真正意义上的基于“悟”的转化。基于“悟”的转化一定是基于“心”的转化，也就是说从“误”到“悟”的过程是基于心理变化的行为转变，因而，它包括“经历发现——寻求理解——重建概念——生成经验”四个阶段。

[1][2]马立平.小学数学的掌握与教学[M].上海：华东师范大学出版社，2011：3，11.

[3]宋乃庆，张奠宙.小学数学教育概论[M].北京：高等教育出版社，2008：94.

[4]张奠宙，孔凡哲，黄建弘，等.小学数学研究[M].北京：高等教育出版社，2009：78.

[5][6][7]安德烈·焦尔当.学习的本质[M].杭零,译.上海：华东师范大学出版社，2015：15，16，28，29.

[8]Randall Curren.教育哲学指南[M].彭正梅，等，译.上海：华东师范大学出版社，2011：304.