稳健总体最小二乘法一元线性回归的相对有效性探讨

2018-01-13刘清葛永慧

统计与决策 2017年24期

刘清，葛永慧

0 引言

线性回归模型是用于解决数理统计问题中变量之间关系的常规模型，最小二乘法是求解其回归系数最经典的方法。最小二乘法在求解回归系数时只考虑线性回归模型中观测值含随机误差的情况，总体最小二乘法（TLS）是为了顾及观测值和系数矩阵同时含有随机误差的状况。然而无论是最小二乘法还是总体最小二乘法都不具有抵抗粗差的能力，当观测值或系数矩阵中包含粗差时，参数估计的结果将会被歪曲[1]。

由于测量人员的工作疏漏以及仪器精密度不同等各种主观因素，数据采集过程中粗差会不可避免地出现。为了剔除或减弱粗差对参数估计的影响，在回归分析中应用稳健估计原理，定义稳健回归的理念。RLS法仅能顾及误差方程中观测向量含粗差的情况，因此，在RLS法的基础上提出了RTLS法——作为一种可顾及系数矩阵和观测向量中涉及粗差的参数估计方法被提出。一些学者将RTLS法引入到线性回归模型中，并通过个别算例中RTLS法得到比RLS法更小的单位权中误差和精度较高的参数解，从而得出在线性回归中RTLS法比RLS法更为有效的结论。

稳健最小二乘法（RLS）的研究已取得了大量的研究成果[2]，稳健总体最小二乘法（RTLS）的研究也取得了一些成果。杨娟等[3]同样把基于稳健估计的TLS法应用于GPS高程异常拟合问题，指出基于稳健估计的TLS法能更好地解决GPS高程拟合模型中控制点已知坐标含误差的问题。陈玮娴等[4]提出了稳健总体最小二乘方法为了解决误差模型中观测值含有粗差的状况，并以小角度坐标转换得出当两套坐标均含随机误差且未含粗差时TLS法优于LS法，当两套坐标均含随机误差且观测值同时受粗差影响时RTLS法优于TLS法。汪奇生等[5]针对线性回归中自变量和因变量可能含有粗差的情况，提出线性回归模型的稳健总体最小二乘算法，并以一元线性回归为例，得出RTLS法较LS法、TLS法、RLS法能更有效地剔除粗差。

迄今为止，并没有明确的理论研究说明在一元线性回归中RTLS法的相对有效性，如果仅仅通过特殊或极个别算例就论证在线性回归中稳健总体最小二乘法一定优于稳健最小二乘法太过片面，并不足以让人信服。其次，判断两种参数估计方法的相对有效性的比较指标应选取均方误差，并不能简单地以单位权中误差来衡量精度。基于上述分析，为了更精确地进行测量数据处理和后续理论的研究指导，对稳健总体最小二乘法在一元线性回归中的相对有效性加以分析研究，仍具有一定的迫切性和必要性。

1 模型分类和方法

1.1 线性回归误差影响模型的分类

测量数据不可避免地会受随机误差和粗差的影响，当运用不同的参数估计方法或建立不同的函数模型时，使得不同的测量数据在参数估计模型中所起的作用也不相同。因此，对一元线性回归中观测值和系数矩阵受粗差和随机误差不同影响的变化情形下，划分为三种不同的误差影响模型，如下：

模型1：此误差影响模型中仅观测值含有随机误差和粗差，系数矩阵不含随机误差和粗差。即线性回归模型中体现为仅因变量含随机误差和粗差。

模型2：此误差影响模型中仅观测值含随机误差，系数矩阵含随机误差和粗差。即线性回归模型中体现为自变量含随机误差和粗差，因变量仅含随机误差。

模型3：此误差影响模型中观测值含随机误差和粗差，系数矩阵仅含有随机误差。即线性回归模型中体现为因变量含随机误差和粗差，自变量仅含随机误差。

1.2 稳健估计方法

6种常用的稳健估计方法如下[2]：

（1）Huber法：

（2）L1法（残差绝对和最小法）：

（4）German-McClure法：

（5）IGG方案：

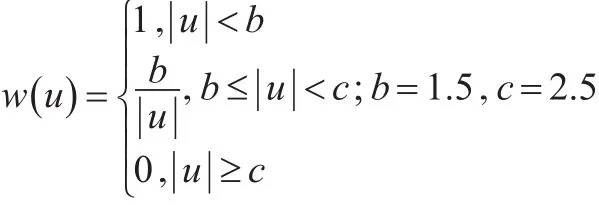
（6）IGGⅢ方案：

1.3 比较参数估计方法的指标[2]

（1）残余真误差均方误差（参数估计的绝对指标）

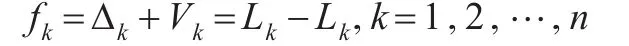
其中，设观测值为Lk；观测值真值由L͂k表示；由参数估计方法获得的Lk的估值由L̂k表示；Lk的真误差由Δk表示；由参数估计方法获得的Lk的改正数由Vk表示。其

残余真误差均方误差（Mean Square of Residual True Error），由MSRTE表示：

σ̂f为残余真误差均方误差，此指标能从根本上将参数估计方法的优劣性和有效性进行实质说明。用统计学的思想对比两种参数估计方法的相对优劣性和相对有效性，针对同一个参数估计问题，相同参数估计方法进行1000次仿真实验所获取的MSRTE的平均值定为残余真误差均方误差[6]，由σ̂f来表示。

（2）参数估计的MSRTE之比（相对指标）

在同一参数估计问题中，σ̂fa表示由方法A得到的MSRTE，σ̂fb表示由方法B得到的MSRTE，令：

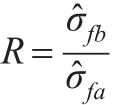
R称为残余真误差均方误差比。式中，是A方法得到的MSRTE，是B方法得到的MSRTE。当R＞1.0时，A方法优于B方法；当R＜1.0时，B方法优于A方法;当R趋向于1.0时，A和B两种方法等价。R作为能从实质上对两种参数估计有效性根本说明的指标存在。继而，运用统计学的思想对两种参数估计方法的相对有效性进行说明，和通常是指A、B两种参数估计方法对于同一个参数估计问题仿真实验多次（如1000次）的平均值。

在本文中，RTLS法得到的观测值（回归系数）估值的残余真误差均方误差与RLS法得到的观测值（回归系数）估值的MSRTE之比用指标RR特指，从根本上说明在一元线性回归中，稳健最小二乘法和稳健总体最小二乘法的相对有效性。

2 算例、实验与讨论

2.1 算例

一元线性回归模型的理论方程为：

从区间[10,37]中任意选取10个均匀分布的数为x，并通过上述方程获取真值Y͂i，组成10对点作为理论模拟值。由模拟观测真值Y͂i、x，在三种不同误差影响模型下，加上包含粗差ε=10σ0、其余服从正态分布N(0，0.12)的随机误差得到相应的模拟观测值yi、xi。

以稳健估计Huber法计算结果为例，运用RLS法和RTLS法分别进行参数估计运算，得出观测值的改正数V、观测值估值的残余真误差以及回归系数估值â0、â1和回归方程，并通过观测值估值的残余真误差fk计算观测值估值的MSRTE以及通过回归系数估值â0、â1计算回归系数估值的残余真误差。其中，RTLS具体计算步骤参照文献[5]。三种误差影响模型下RLS法和RTLS法的模拟观测数据和实验结果见表1。观测值（因变量）真值由Y͂i表示，其中元数由i表示，i=1，2，3。x表示自变量真值，Δ表示服从正态分布N(0，0.12)的随机误差，y表示由Y͂i和随机误差Δ、粗差ε=10σ0共同生成的模拟观测值。RLS法的观测值改正数由VA表示，RLS的残余真误差由△A表示。RTLS的观测值改正数由VB表示，RTLS的残余真误差由△B表示。

表1 模拟观测值和真值与RLS法和RTLS法的实验结果

由RLS 法计算得到的回归系数估值â0=3.0233，â1=0.2481。回归方程：

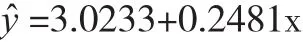
由表1中△A列数据可计算得到RLS法观测值估值ŷ的MSRTE为：σ̂f1=0.73。

RTLS 法得到的回归系数估值â0=1.0436，â1=0.3338。回归方程：

由表1中△B数据得到的RTLS法的ŷ的MSRTE为：σ̂f2=1.05 。

观测值估值ŷ的RTLS法和RLS法的残余真误差均方误差比：

通过一次计算就可以获得观测值估值ŷ的MSRTE，对于仿真1000次实验计算，取其平均值作为观测值的MSRTE。

由RLS法计算得到回归系数估值â0的残余真误差为Δ3=â0-a͂0=0.7733 ，回归系数估值â1的残余真误差为Δ4=â1-a͂1=-0.0019 。

回归系数估值â0通过RTLS法得到的残余真误差为Δ3=â0-a͂0=-1.2064 ，回归系数估值â1的残余真误差为Δ4=â1-a͂1=0.0838 。

回归系数估值的残余真误差可以通过一次仿真实验计算出，其残余真误差均方误差可由1000次的仿真实验计算出。

2.2 一元线性回归的仿真实验

当给定a͂0、a͂1和自变量x的取值时，就可通过一元线性回归的理论模型y͂=a͂0+a͂1x得到理论模拟值，通过运用三种不同误差影响模型，由理论观测值加上随机误差或粗差生成模拟观测值。

选取三组不同斜率的一元线性回归方程：A组、B组、C组，分别为斜率约为tan15°、tan45°、tan75°的一元线性回归模型，相对应的理论回归方程为：y͂=2.25+0.25x、y͂=2.25+1.05x、y͂=2.25+3.75x。

在上述A、B、C三组方程中分别根据三种不同误差影响模型、不同稳健估计方法在观测值n=6(n表示观测值个数)的情形下进行仿真实验。

以观测值n=6为例，由上述三种不同斜率（tan15°、tan45°和tan75°）的一元线性回归模型生成的理论模拟值见表2。

表2 不同斜率的理论模拟值（n=6）

理论模拟值加上随机误差或粗差（ε=10σ0）生成模拟观测值。对于观测值n=6、三种不同的斜率、三种不同误差影响模型的情形分别进行1000次仿真实验（方法同算例2.1）。

n=6，ε=10σ0时RLS和RTLS得到的观测值估值ŷ的残余真误差均方误差见表3，由表3可计算得RTLS与RLS观测值估值ŷ的残余真误差均方误差之比见表4，回归系数的估值â0和â1通过RTLS和RLS所获得的MSRTE之比见表5。

表3 RLS和RTLS的观测值估值ŷ的残余真误差均方误差(n=6，ε=10σ0)

表4 RTLS和RLS的观测值估值 ŷ的MSRTE之比(n=6，ε=10σ0)

表5 RTLS和RLS的回归系数的估值â0和 â1MSRTE之比 (n=6，ε=10σ0)

（1）第一种误差影响模型（仅观测值（因变量）含有粗差和随机误差）

对于A、B、C三组不同斜率（tan15°、tan45°和tan75°）以及观测值（因变量）含有粗差和随机误差的情况，通过RLS和RTLS发现所得到的观测值估值ŷ的残余真误差均方误差之比（表4）都有RRi＞1.0；RTLS和RLS得到的回归系数的估值 â0和 â1的残余真误差均方误差之比（表5）是绝大多数情况下RRi＞1.0和个别情况下RRi接近1.0。所以RLS无论是对于观测值估值ŷ还是对于回归系数的估值â0和 â1相对于RTLS都更有效。

（2）第二种误差影响模型（系数矩阵含有随机误差和粗差，观测值仅含有随机误差的）

对于6种常用的相对有效稳健估计方法，RTLS和RLS在斜率约为tan15°时，所获得的观测值估值ŷ的残余真误差均方误差之比（表4）是绝大多数情况下RRi＞1.0和个别情况下RRi接近1.0，RLS相对于RTLS更有效；RTLS和RLS在斜率约为tan45°时，所获得的观测值估值 ŷ的残余真误差均方误差之比（表4）1.50＞=RRi＞=0.52，RLS和RTLS有效性很难被说明；RTLS和RLS在斜率约tan75°时，所获得的观测值估值ŷ的残余真误差均方误差之比（表4）有 RRi＜=0.27；RTLS相对于RLS更有效。

对于（tan15°、tan45°和tan75°）这三种不同的斜率以及6种常用的相对有效的稳健估计方法而言，通过RTLS和RLS计算获取的回归系数估值 â0和 â1的MSRTE之比（表5）在绝大多数情况下RRi＞1.0和个别情况下RRi接近1.0。RLS 对于回归系数的估值 â0和 â1比 RTLS 更为有效。

（3）第三种误差影响模型（观测值含有随机误差和粗差，系数矩阵仅含有随机误差）

对于A、B、C三组不同斜率（tan15°、tan45°和tan75°）以及6种常用的相对有效的稳健估计方法而言，RTLS和RLS得到的观测值估值 ŷ的残余真误差均方误差之比（表4）是绝大多数情形下RRi＞1.0和个别情况下RRi接近1.0；RTLS和RLS得到的回归系数的估值 â0和â1的残余真误差均方误差之比（表5）都有RRi＞1.0。即无论是观测值估值 ŷ还是回归系数的估值 â0和 â1，RLS相对于RTLS更有效。

利用类似的方法，对和n=10和ε=10σ0的情形进行了类似的仿真实验，所得到的结果与ε=10σ0和n=6的情形相同。

3 结论

本文用不同的误差（粗差）影响模型、不同的稳健估计方法和不同的斜率，运用仿真实验的方法，讨论了一元线性回归中RLS法和RTLS法的相对有效性。

针对A、B、C三组（斜率约为tan15°、tan45°和tan75°）的一元线性回归模型：就观测值（因变量）的估值而言，在第一种和第三种误差影响模型下，RLS优于RTLS。在第二种误差影响模型下，当斜率较小（约tan15°）时，RLS比RTLS相对更为有效；当斜率约为tan45°时，难以说明RTLS与RLS哪个更有效；当斜率较大（约tan75°）时，就RLS而言RTLS相对更为有效。在三种不同的误差影响模型下，针对回归系数的估值而言，RLS始终都比RTLS相对更为有效。因此，综上所述，对于一元线性回归RTLS相对于RLS并没有明显的优越性。

[1]孙同贺，闫国庆，周强波.稳健初值的选权迭代法剔除DEM数据粗差[J].测绘科学，2011,36(3).

[2]葛永慧.再生权最小二乘法稳健估计[M].北京：科学出版社，2015.

[3]杨娟，陶叶青.GPS高程异常拟合的文件总体最小二乘算法[J].大地测量与地球动力学，2014,34(5).

[4]陈玮娴，袁庆.抗差总体最小二乘方法[J].大地测量与地球动力学，2012,32(6).

[5]汪奇生，杨德宏，杨腾飞.线性回归模型的稳健总体最小二乘解算[J].大地测量与地球动力学，2015,35(2).

[6]葛永慧.再生权最小二乘法研究[J].测绘通报,2014,(8).