基于自更新网格的变异多目标粒子群算法
2018-01-12金维佳
金维佳
(浙江工商职业技术学院,浙江 宁波 315012)
1 引言
粒子群算法 (Particle swarm optimizer,简称PSO)是由J.Kennedy和R.C.Eberhart[1]提出基于对鸟群捕食行为的研究而提出的一种进化算法。PSO算法在很多领域的实验中都有出色的表现,并且不需要调节很多的参数。但是,算法中有几个少数的参数却直接影响着算法的收敛性和效果。所以,也有很多学者对惯性权重提出了改进方案,比如Shi和Eberhar[2]提出根据迭代次数线性递减来改进算法。
在现实世界中,许多优化问题并不只是单目标的,大量实际应用问题都需要转化为多目标问题才能进行全面的优化。在2004年,C.A.C.Coelleo等[3]首次提出多目标粒子群算法(MOPSO)。粒子对于每个目标的适应度都要比较高,才能算优,并且要选择领导者和进行非劣解的存档。然而,在实际操作中面临两大困难,分别是引导粒子向Pareto前沿的收敛和维护所得解的多样性。因此,产生了大量的改进,比如基于种群划分的多目标粒子群算法(CMOPSO)和加入压缩因子的多目标粒子群算法(SMOPSO)[4],但这些算法在全局最优粒子的选择和搜索能力的平衡上存在着不足。在这基础之上,一些引导者选择策略也被相继提出,比如基于最小角度的粒子引导者选择策略、多目标骨干粒子群优化和目标分割等策略,虽然能较好地避免早熟问题和保持解的多样化[4],但是实现过程比较复杂。
因此,本文提出一种相对简易有效的多目标粒子群算法,即通过变异算子来选择群体领导者,避免过早收敛,并根据非劣解的密度来自动更新划分网格,以提升选择概率来提高解的多样性。具体方法和步骤如下。
2 研究方法
在此部分,本文会先介绍PSO和多目标优化问题的具体概念,然后再提出自更新网格的多目标粒子群变异算法的实现步骤。
2.1 PSO算法
PSO算法的主要思路是每个飞鸟都是一个粒子,代表了一个对于优化问题的潜在解,通过粒子的个体习惯和社会行为来确定最优解用代表个体习惯的公式(1)和代表社会行为的公式(2)来迭代以求得最优解。假设在一个D纬的目标搜索空间中,时间序列T上的t时间点上,种群有N个粒子。其中第i个粒子,在t时间里是D维空间的一个向量xij(t),而第i个粒子的速度也是一个D维向量vij(t)。第i个粒子迄今为止找到的最优位置即个体极值是,而整个粒子群迄今为止的最优位置是全局极值是pij(t),以下是粒子用来更新速度和位置的公式:
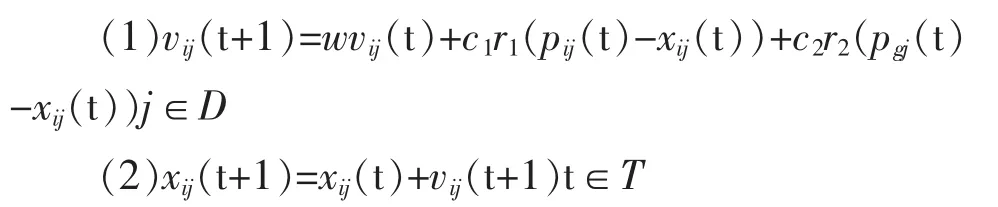
这里,w是惯性权重,反应了粒子本身的运动习惯;c1,c2是学习因子,也是加速常数,通常取值在2左右;r1,r2是[0,1]之间的随机数。
2.2 多目标问题的优化
多目标优化问题的数学描述如下:
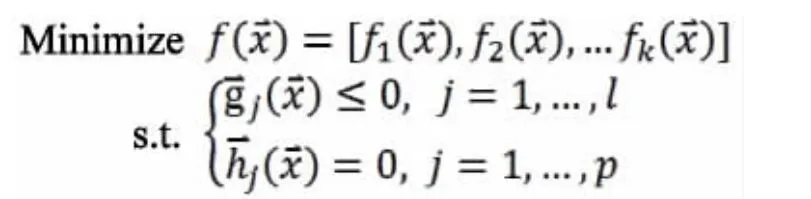
2.3 自更新网格的多目标粒子群变异算法(AGM-MOPOS)
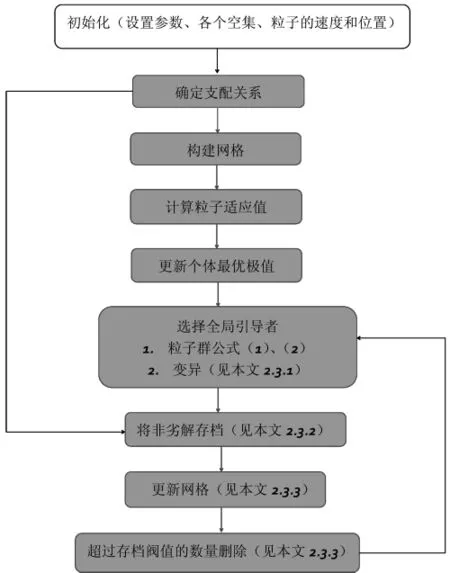
2.3.1 变异算子
前面提到过PSO算法所需要的参数不多,并且收敛速度较快,但正因为如此很可能导致收敛过早和局部的Pareto前端。为了避免早熟,本文采用一种经常使用的变异算子来优化算法。设当前迭代次数是Itr,总迭代次数MaxItr,变异因子mu。以下是变异算子主循环的伪代码:

2.3.2 外部存档与规模
此算法会生成空的外部存档的矩阵,然后粒子群在经过每一次迭代以后都会产出一组非劣解并更新外部存档,并与当前已存在的非劣解逐一比较,淘汰劣解。同时,要对外部存档限制规模。因为,随着迭代次数的增多,保留下来的非劣解也随之增长,算法的复杂度也会不断地升级,其中是迭代次数;是目标个数;是种群规模。文献[4]介绍了一种根据储备集中分布密度来限制规模的多目标骨干粒子群算法,但鉴于其算法复杂度较高,本文将采用自适应网格中非劣解的密度来确定全局的引导者。
2.3.3 自更新网格的构建和阀值
自适应网格的构建就是将D维空间的每个维度分为 k 份, 也就是 k1,k2,...kD对应每个维度的搜索空间。 所以,D 维目标空间就变成了 k1×k2×...×kD的网格。本次研究将每个维度的网格数量设定为7,也就是k1=k2=...=kD=7.每一次迭代,非劣解就落在以网格为划分的坐标里,就可以确定每个网格里非劣解的个数,也就是非劣解的密度。在同等筛选条件下,每格网格中密度值越低,粒子被选择的概率就越大,所以可以保证算法的全局搜索能力,也能保证解的多样性。当存档里的元素数量超过最大容量也就是阀值的时候,根据网格里非劣解的密度和比率选择非劣解删除。
综合2.3.1-2.3.3的内容,可将AGM-MOPOS算法作下图表述。
3 结果和分析
本文首先采用基准函数ZDT1来测试算法的paroto前沿的表现,将ZDT1的两个目标函数命名为1stobjective function和2ndobjective function.迭代次数设置为200次,粒子群规模设置为200,储备集最大容量为100,惯性权重是0.5,阻尼频率是0.99,变异速率是0.1。把红色的雪花形作为全局引导者的标记,黑色三角形作为非劣解的标记,运行结果如图1所示,收敛情况比较理想,分布也较均匀。
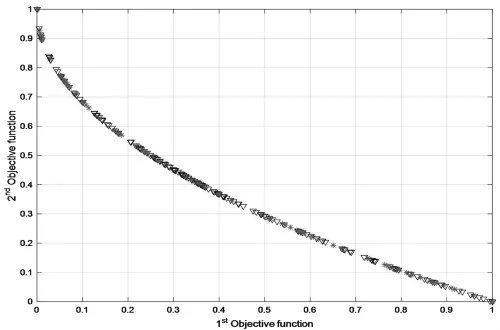
图1 算法的Pareto前端
为了更好地体现该算法的性能,本文在种群规模为100,储备集最大容量为100,迭代次数为150的条件下,在基准函数ZDT1上,用GD和SP测度检测它的性能,并与同等条件下的其它三种算法的运行性能进行比较。这三种算法是在引言部分提到过的CMOPOS和SMOPSO算法,以及应用广泛的多目标遗传 NSGA-II。

表1 4种算法优化函数ZDT1所得关于GD、SP测度的结果
GD是利用迭代距离评价Patero前端和真实Pareto前端的测度,越接近0,表明解越接近真实的Pateto前端。SP是评价所得Patero前端上所有点的等距情况,越接近0,表示解分布得越均匀。AV表示平均值,VAR表示方差。可以从表1看出,AGMMOPSO虽然未在每项性能测度中胜于其它算法,但是综合看来各项指数来看,仍具有理想的性能。
4 结语
实验证明通过变异因子和更新网格等方法,可以使MOPSO算法的非劣解较为均匀地分布,保持算法的多样性。并且,本文认为PSO的这种源于群体性活动的内在逻辑非常适用于对社会群体的行为研究。
[1]Kennedy J,Eberhart R.Particle swarm optimization,neural networks[C].Proc of IEEE IntConfon Neural Netw o rks.Perth, 1995:1942-1948.
[2]Shi Y,Eberhart R.A modified particle swarm optimizer[C].IEEE World Congress on Computation Intelligence.Anchorage, 1998:69-73.
[3]Coello C A C,Pulido G T,Lechuga M S.Handling multiple objectives with particle swarm optimization[J].IEEE Transon Evolutionary Computation,2004,8(3):256-279.
[4]张勇,巩郭卫.先进多目标粒子群优化理论及其应用[M].北京:科学出版社,2016.
