压电陶瓷精密位移系统的变论域模糊控制法
2018-01-12
(郑州轻工业学院 机电工程学院,郑州 450002)
压电陶瓷驱动器(PZT)是利用其逆压电效应从而实现位移的输出的执行器件。压电陶瓷驱动器具有体积小、响应快、集成度高等特点,克服了传统位移执行器精度不足且机构复杂等问题。在光学精密工程、微机械系统、MEMS技术等领域都有广泛的应用[1]。
在高精密定位系统当中,应用较为广泛的就是压电陶瓷驱动器,通过陶瓷两端施加高电压,即可实现位移的输出。但是由于压电陶瓷本身的迟滞性和蠕变性,极大地限制了其在控制过程中的输出精度。通过构建一个闭环控制系统,实现对压电陶瓷的实时控制,相比于传统的PID控制系统,模糊控制(fuzzy)系统能够在线整定控制参数,将PID控制与模糊控制结合形成模糊PID控制(fuzzy-PID)有更为优秀的控制效果。进一步,模糊控制当中较为依赖模糊规则的制定且模糊控制过程能对PID参数进行改变,但是模糊控制器并没有随着控制过程发生变化,因此通过对论域的改变,也就是对伸缩因子的改变,从而形成了变论域模糊PID控制,最终应用于压电陶瓷位移系统。
1 压电陶瓷定位系统
本文涉及的压电陶瓷微定位系统,由压电陶瓷驱动电源、PZT、定位机构、测微仪和数据采集卡(NI ELVIS II)构成,如图1所示。采用苏州博实公司生产的HPV驱动电源,输出电压 (Ui)对PZT(SABS型)进行驱动,测微仪选取电容测微仪(LVDT型)对输出位移(Xout)进行测量,最终将测量的数据汇入数据采集卡当中,通过电脑当中的LabVIEW软件,对输入和模拟输出进行控制。
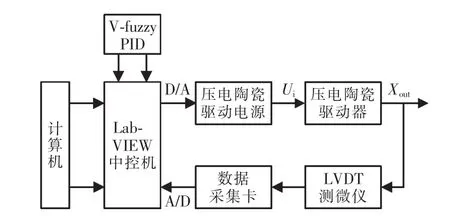
图1 微位移系统硬件控制框图Fig.1 Hardware block diagram of micro-displacement system
2 压电陶瓷的数学模型
2.1 压电陶瓷的原理
压电陶瓷具有正、逆压电效应,在施加电压与作用力的情况下分别输出位移和电压。本文主要针对其逆压电效应,在强电场的作用下,压电陶瓷内部的电介质发生形变,从而产生了位移,其位移大小与电场的大小成正比,压电系数与其内部压电陶瓷电荷密度等有关系。因此PZT由于工艺不同,其输出曲线也不尽相同,经过试验可知,在施加电压较小时,其输出曲线呈现线性关系。随着电压增加,压电陶瓷的伸缩效应增加,但同时由于压电陶瓷的蠕变性和迟滞性,其输出曲线呈非线性的特点。
2.2 压电陶瓷电容模型
压电陶瓷在施加电压时,由于其内部晶体的运动,有蠕变性和迟滞性等特点,因此传统的数学模型分析较为繁琐。压电陶瓷两端施加电压的共振频率较高,一般高于10 kHz,远远大于共振频率,因此在实际应用当中,压电陶瓷可以看做电容、电感和电阻的等效电路模型,如图2所示[2]。

图2 压电陶瓷等效模型Fig.2 Eqivalent model of PZT
由ΣUi=0,和ΣIi=ΣIo可得:

此外

即

对式(5)拉普拉斯转换后可得:

由压电陶瓷本身特性考虑,在施加电场的情况下,压电陶瓷的输出位移与其内部电荷之间的关系为[3]
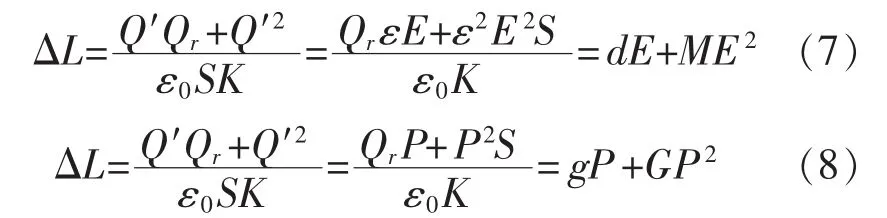
即:

根据简化后的模型,PZT将其作为一个惯性环节的表现,因此可以得到压电陶瓷自身特性与位移与电压的关系为

式中:dc为PZT位移转换系数;τ为工作时惯性环节的时间常数;k为压电陶瓷叠片的弹性模量。
因此可以得到压电陶瓷在被施加电压时的数学模型为[4]
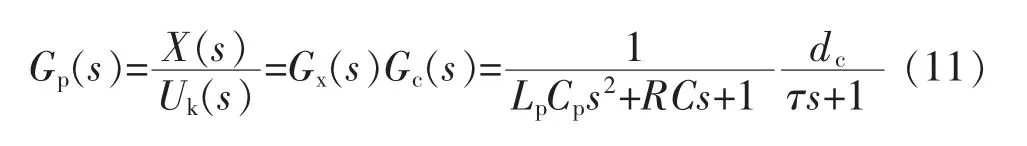
3 变论域模糊控制器的设计
3.1 模糊PID控制器
PID控制器是工业工程中应用最为广泛的控制器,其通过在控制过程中的比例、积分、微分组成控制量,从而对被控对象进行实时控制[5]。

模糊PID控制是将PID控制与模糊控制相结合,通过对控制过程中的误差e以及误差变化率ec的变化的分析,经过模糊控制器规则库的推理,最终控制比例、积分、微分3个控制参数的大小,从而实现对目标的实时控制,模糊推理规则库的精确程度直接关系推理精度,规则库越复杂精确,则输出变量越精确。
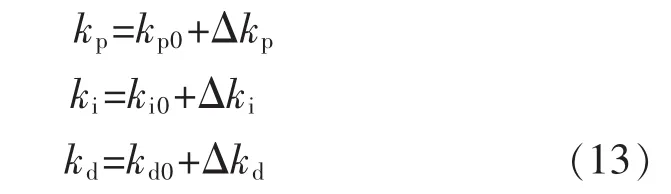
式中:kp0,ki0,kd0是 PID 控制器初始控制变量;Δkp0,Δki0,Δkd0是经过模糊推理后的输出变量。其控制器结构如图3所示。

图3 模糊控制器模型Fig.3 Fuzzy controller model
控制器采用双输入(e,ec)、三输出(Δkp0,Δki0,Δkd0)的结构形式,为了计算简便,将输入和输出变量的模糊控制论域同时设定为{-E,E},其推理的模糊子集设定为[NB,NM,NS,ZO,PS,PM,PB],并给出量化等级。利用Matlab中的模糊推理工具箱,对模糊规则和模糊语言进行设定,本文只给出Δkp0的模糊控制规则,如表1所示。
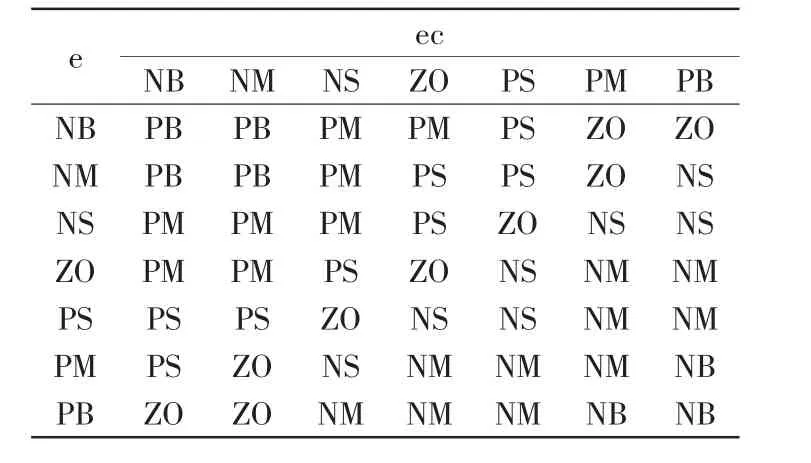
表1 kp0的模糊控制规则Tab.1 Fuzzy control rule of kp0
模糊推理中有Mamdani法、Larsen法、Zadeh法等,本文采用常见的Mamdani法进行推理,解模糊则采用加权平均解模糊方法,如下:

根据系统的实际运行的动态范围,e=[emin,emax],ec=[ecmin,ecmax],Δkm=[Δkmmin,Δkmmax]。因此论域的变换公式为[6]

式中:Ke、Kec、LK(m)为确定量化因子和比例因子。
3.2 变论域模糊控制器
模糊PID控制器比一般的PID控制器在控制效果上有更优秀的表现,但是相比于其他智能控制方法,模糊控制器在控制前期一旦确定控制策略则无法更改,这样就限制了其自适应控制的能力。李洪兴教授最早在1997年提出了模糊控制器的智能“升级”,也就是将控制过程中,控制变量的论域随着误差的变化而变化。这样是为了避免当误差在较大范围内变化时,论域也会增大,随之会带来相对控制规则的减小、控制精度的降低。而变论域的策略能在控制过程当中实现论域的智能增大或者缩小[7]。
模糊控制的本质就是插值器,而变论域的工作方式就是变相地对插值进行加密,变相地增大控制的规则。其控制原理如图4所示。
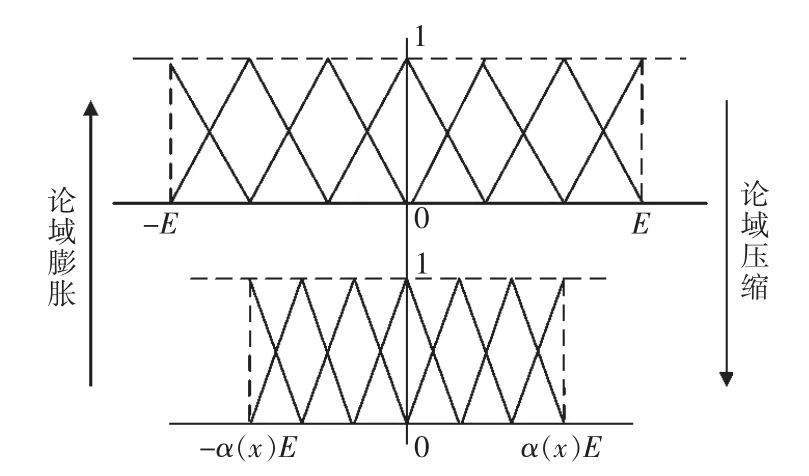
图4 变论域工作原理Fig.4 Working principle of variable-universe
若模糊控制器的输入的论域为[-E,E],输出的论域为[-U,U],通过论域伸缩因子α(x)、 β(y),z 则论域变化为[-α(x)E,α(x)E]、[-β(y)U, β(y)U]。
因此伸缩因子α、β分别为[8]
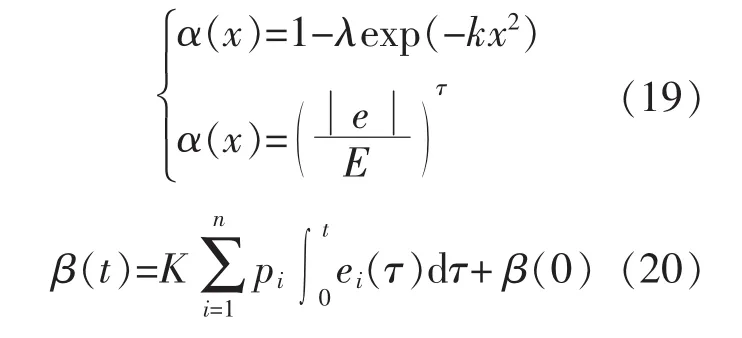
式中:λ∈(0,1);k>0;0<τ<1;K 为比例常数; β(0)取0。
在变论域模糊控制器中,根据误差e以及误差变化率ec的变化,作用于输入与输出量的伸缩因子(α(x)、β(y)),通过伸缩因子的改变,最终作用于模糊控制器的比例因子 (LK(m),m=1,2,3)和量化因子(Ke、Kec)。 控制过程中,由式(16)可知,比例因子增大,则输出论域增大;量化因子增大,则输入论域减小,反之亦然。因此变论域模糊控制器的实质就是改变控制器的比例因子与量化因子从而得到论域改变的效果,提高控制精度。其控制框图如图5所示。
3.3 系统仿真机及结果
用Matlab中Simulink环境下分别对压电陶瓷微位移系统、变论域自适应模块、模糊PID控制器和传统PID控制器进行建模。由于Matlab不提供变论域模糊控制箱,因此一般使用S函数或者使用Simulink独立对模糊控制模块进行建模。本文使用Simulink对变论域模块直接进行建模,如图6所示。将变论域模糊控制模块与模糊PID控制器(图7)结合,最终形成了自适应模糊PID控制系统。为了避免在建模过程中各部分排布混乱,因此将3种控制器分别整合为子系统,并布局在同一输出下,如图8所示,从上至下分别为变论域模糊控制系统、模糊PID控制系统和PID控制系统。

图5 变论域控制器工作原理Fig.5 Principle of variable-universe controller

图6 变论域控制模块Fig.6 Model of variable-universe controller

图7 模糊PID控制模块Fig.7 Module of fuzzy-pid controller

图8 三种控制方法Fig.8 Three kinds of control method
3.4 系统仿真
利用Matlab进行仿真,设定输入阶跃响应为1,仿真时间为10,选用定步长方式,算法选取ode3(bogacki-shampine)。对图8所示的仿真模型进行仿真,仿真结果如图9所示。仿真结果显示,3种控制方法达到稳态的时间分别为1.9 s、3.2 s和3.7 s,可以看出随着时间的增加,变论域控制效果越来越明显,其曲线的上升速度明显变快,能够快速地达到稳定状态。

图9 三种控制的方法的阶跃响应曲线Fig.9 Step response curves of three control method
在系统为t=6时,加入振幅为0.4、周期为10的干扰信号,设定其占空比为1%,可以看出变论域模糊控制器对干扰的稳定效果比模糊PID与PID控制更优秀,在扰动发生开始到恢复稳定状态时间要比其它2种方法短,具有较好的鲁棒性。
4 结语
变论域模糊PID控制方法将模糊控制器与PID控制器相结合,不仅仅能够在线整定比例、积分、微分3个控制参数,而且还能对模糊控制器的论域进行调节,变相地扩大了控制规则,提高了控制精度。一般在模糊控制器能够使用的情况,变论域控制系统都能适用,经过仿真结果可以看出,该方法能够表现出更为优良的控制效果,特别是在对于压电陶瓷这种具有大迟滞性等特点的非线性模型。在面对干扰的情况下,变论域模糊PID控制器也有不错的表现,抗干扰能力强,具有良好的工程应用前景。
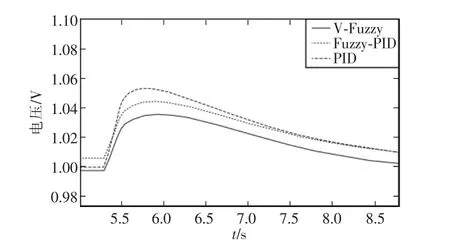
图10 干扰控制曲线Fig.10 Interfence control curve
[1]刘泊,郭建英,孙永全.压电陶瓷微位移驱动器建模与控制[J].光学精密工程,2013,21(6):1503-1509.
[2]林伟,叶虎年,叶梅.一种新型压电陶瓷控制器的研究[J].压电与声光,2005,27(3):247-249.
[3]张涛,孙立宁,蔡鹤皋.压电陶瓷基本特性研究[J].光学精密工程,1998,6(5):26-32.
[4]刘建秀,张杨,张段芹.压电陶瓷精密控制系统的自适应模糊控制器研究[J].压电与声光,2015,37(5):806-809.
[5] 刘金琨.先进PID控制及其MATLAB仿真[M].北京:电子工业出版社,2003:67-80.
[6]王宏文,吴红星,孟立新,等.变论域模糊PID在无头轧制模拟实验台上的研究[J].电气传动,2016,46(6):71-75.
[7]李洪兴.Fuzzy控制的本质与一类高精度Fuzzy控制器的设计[J],控制理论与应用,1997,14(6):868-871.
[8]李洪兴.变论域自适应模糊控制器[J].中国科学,1999,29(1):32-42.
