基于自抗扰的四旋翼飞行器姿态控制

（天津工业大学 电气工程与自动化学院，天津 300387）

四旋翼飞行器是一种能够实现垂直起降、悬停、偏航等复杂动作的多旋翼无人机，因而在军事和民用领域的应用前景十分乐观[1]。它是一种强耦合、欠驱动系统，结构复杂，所以要对其进行很好的控制是有难度的，经过许多科研人员的不懈努力，国内外在飞行器控制器方面取得了一些研究成果。

飞行器控制器的设计中，姿态控制是整个控制的关键[2]。目前国内外在控制器方面的主要控制方法有PID[3]、反步法、自适应[4]等。但是上述控制方法使用的前提是飞行器模型和参数都是精确且已知的，在实际飞行时系统会受到周围环境等各种不确定未知因素的影响。文献[5]利用自抗扰技术实现了三自由度四旋翼系统的姿态跟踪；文献[6]研究了基于自抗扰技术的四旋翼姿态解耦控制方法；文献[7]研究了基于自抗扰技术的四旋翼盘旋系统的姿态控制，然而上述几个都只限于仿真并未将其算法应用于实际的实验平台上。本文基于自抗扰技术设计了四旋翼飞行器姿态控制器，在仿真基础上将其控制算法在本实验室现有平台Qball2的实验平台上进行了测试。仿真和试验结果表明，所设计的自抗扰姿态控制器具有良好的性能，对非线性耦合系统的控制能够达到期望的效果，控制器具有良好的鲁棒性和快速性。

1 四旋翼飞行器

1.1 四旋翼飞行器姿态模型

建立数学模型时忽略陀螺效应和空气阻力等因素。根据动量矩和平衡关系建立方程，记Vf，Vb，Vl，Vr为前后左右4个电机的电压，前后螺旋桨的升力控制俯仰角，左右螺旋桨的升力控制滚转角，4个螺旋桨的升力共同控制偏航角。根据文献[5-7]，得到四旋翼飞行器的姿态模型为

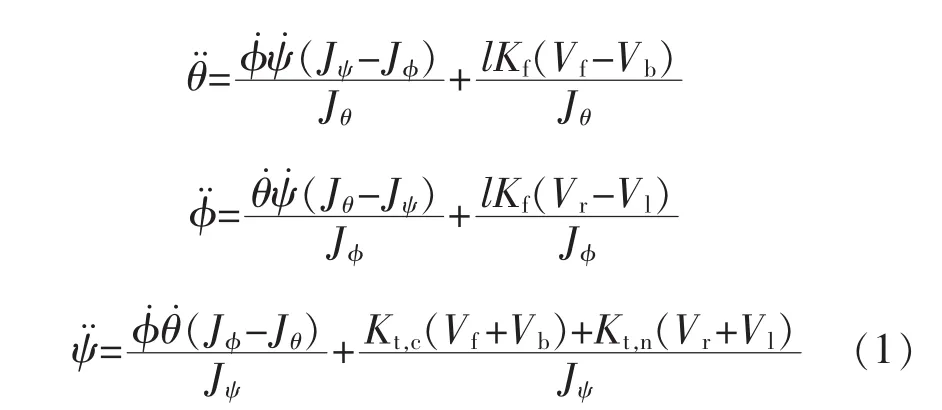
式中：θ，φ，ψ分别表示俯仰角、滚转角和偏航角；Jθ，Jφ，Jψ分别表示俯仰、滚转和偏航轴的转动惯量；l为轴到螺旋桨中心的距离；Kf为升力系数；Kt，c，Kt，n为逆时针和顺时针力矩系数。

由于在实际飞行时会受到各种未知因素的干扰，为了更接近实际系统，仿真时在每个通道中加入一定的白噪声[8]，综上得到四旋翼飞行器的姿态模型为

1.2 姿态模型控制结构

针对上述建立的模型，根据自抗扰原理为3个姿态角通道设计了自抗扰控制器，被控对象的结构如图1所示。为了更好地说明ADRC，其结构如图2所示（以俯仰通道为例）。

图1 被控对象结构Fig.1 Structure diagram of controlled object

图2 俯仰角ADRC部分的结构Fig.2 Structure diagram of ADRC part of pitch

2 自抗扰控制器设计

ADRC由跟踪微分器（TD）、扩张状态观测器（ESO）、非线性状态误差反馈（NLSEF）三部分组成[9]。以俯仰角的控制为例详细说明ADRC 3个部分的控制算法，另外2个通道过程同理。

2.1 离散的非线性跟踪微分器（NLTD）设计

根据自抗扰原理，设计的俯仰通道的离散型NLTD为

式中：θ0（k）为给定的俯仰输入信号；θ1（k）为 θ0（k）的跟踪信号；θ2（k）为 θ1（k）的微分；h 为系统的采样步长；h0为滤波因子；r为速度因子。非线性最速控制综合函数 fhan（x1，x2，r，h0）的形式为

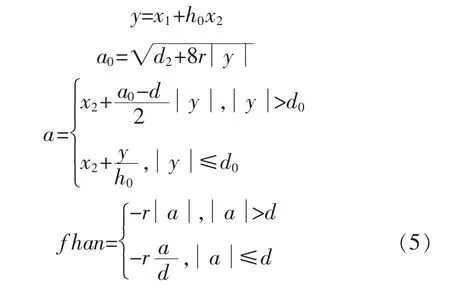
2.2 离散的非线性扩张状态观测器（NLESO）设计

把系统的扰动和未知部分扩张成新的状态变量，用特殊的机制建立扩张状态观测器[10]。根据上节已确定的系统模型，设计的俯仰通道的离散型NLESO为

其中非线性函数为

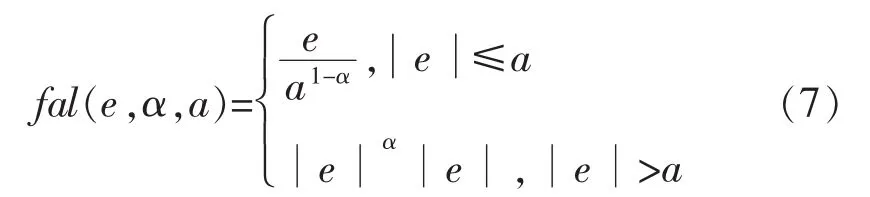
2.3 离散的非线性状态误差反馈（NLSEF）设计

不同的反馈机制可以对系统的扰动产生不同的抑制效果，根据ADRC原理设计的状态误差反馈为

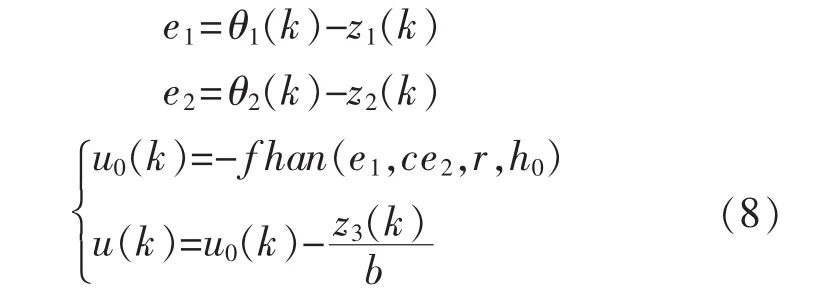
式中：非线性函数 fhan（）的形式如式（5）所示；b 为扰动补偿因子。

3 试验结果

为了验证ADRC控制器的有效性，首先将控制算法在Matlab中进行仿真，然后将其控制算法应用到本实验室Qball2的实验平台上。

本实验室Qball2实验平台是由加拿大Quanser公司研发的适合于多用途研究的四旋翼飞行器平台。4个直流无刷电机对称地安装在飞行器的支架端，整个飞行器机身在一个球状的碳纤维结构里，防止在飞行过程中由于各种原因与障碍物接触，保护和缓冲机身结构和软硬件。Qball2的结构如图3所示。

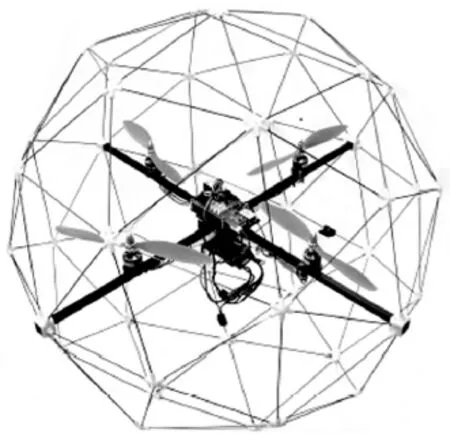
图3 Qball2结构Fig.3 Quanser Qball2

关于ADRC的2个部分都采用Simulink中的edit mask命令进行封装，算法中的非线性函数fhan（）和fal（）用程序编写成.M文件然后再使用Simulink中的Matlab function模块调用该M文件来实现。

本文所选用系统的各个参数值为Jψ=0.04 kg·m2，Jθ=Jφ=0.03 kg·m2，l=0.2 m，Kf=12 N/V，Kt，n=-Kt，c=0.4 N·m/V

由于飞行器特殊的对称结构，所以滚转和俯仰通道选用近似的同一组参数，根据模型偏航通道的参数值和另2个通道相近，在此基础上根据实时仿真和试验情况细调参数，最后确定3个通道控制效果最好的控制器参数 a， β01， β02， β03，c，r，h0，b 为

3个通道的参数：a=0.01

滚转通道：β01=200，β02=100，β03=1200，

c=0.5，r=100，h0=0.01，b=6

俯仰通道：β01=200，β02=110，β03=1100，

c=0.5，r=100，h0=0.01，b=10

偏航通道：β01=100，β02=300，β03=800，

c=0.2，r=50，h0=0.01，b=15

在仿真和试验时都将3个角的期望给定值设为0.1 rad（约为5.73°）。为了进行更好地比较，在仿真时将所设计的自抗扰控制与传统的PID控制进行了对比，最后得到3个姿态角的仿真结果如图4～图6所示。

从仿真图4～图6可以看出，对于ADRC控制3个姿态角都无超调，俯仰和滚转角在大约0.8 s左右进入稳态，偏航角大约1.3 s进入稳态，且之后都没有震荡，完全跟踪上期望值。而PID控制有超调，且进入稳态的时间相对于ADRC来说比较长，所以从仿真对比结果可知ADRC控制具有良好的快速性和鲁棒性。

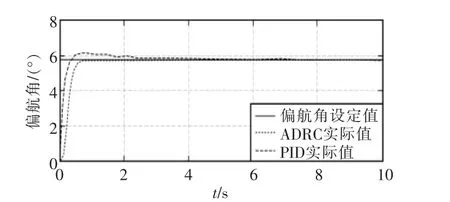
图4 偏航角仿真Fig.4 Simulation graph of yaw angle

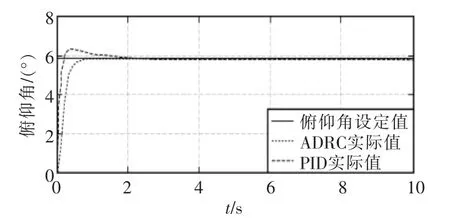
图5 俯仰角仿真Fig.5 Simulation graph of pitch angle

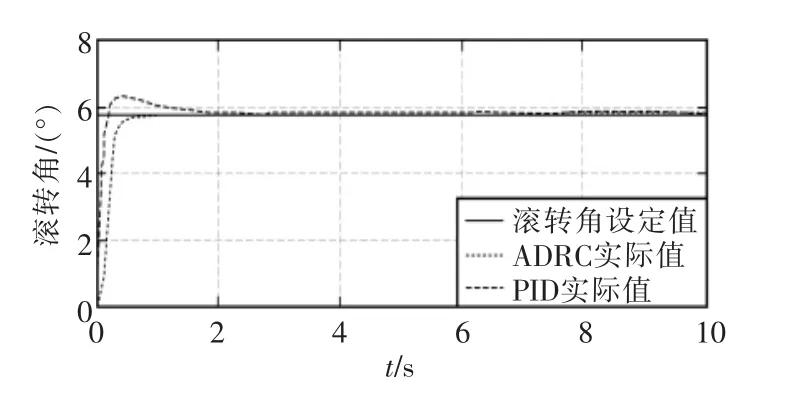
图6 滚转角仿真Fig.6 Simulation graph of roll angle

由于与传统的PID比较ADRC控制具有上述优点，所以将ADRC控制算法应用到了本实验室的实验平台上。得到3个姿态角的试验结果如图7～图9所示。

从试验结果可以看出，稳态后偏航角的误差非常小，俯仰和滚转角的误差稍大，但是误差保持在0.5°～0.7°左右，而进入稳态的时间很短，体现了ADRC控制器的上述优点。

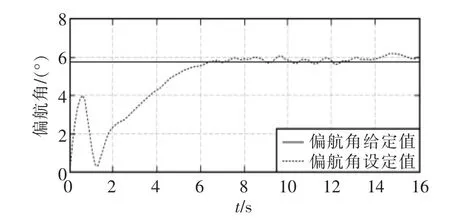
图7 偏航角试验结果Fig.7 Experimental result of yaw angle

图8 俯仰角试验结果Fig.8 Experimental result of pitch angle

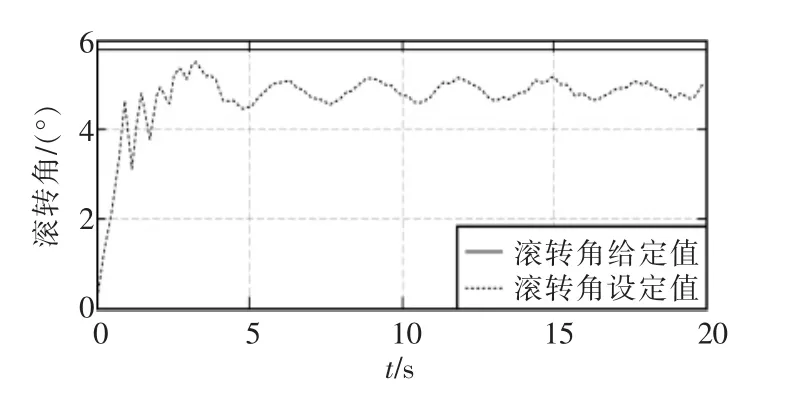
图9 滚转角试验结果Fig.9 Experimental result of roll angle

4 结语

本文设计的ADRC姿态控制器，在Matlab仿真中几乎可以完全且很好地达到期望给定值。但是在实际试验时由于受各种因素的影响，导致实际的控制效果不是很理想，存在小于1°的误差。通过与PID比较和试验结果表明，ADRC控制器快速性和抗干扰性好，对耦合、欠驱动系统能够进行有效的控制。并且控制器参数在一个范围内变化时，其结果也不会发生很大的变化，由结果知ADRC控制超调量小、震荡小、响应时间短，充分体现了ADRC控制的鲁棒性。

[1]方勇纯，申辉，孙秀云，等.无人直升机航向自抗扰控制[J].控制理论与应用，2014，31（2）：238-243.

[2]JiuhongRuan，Yibin Li.ADRC based ship coursecontroller design and simulations[C]//2007 IEEE International Conference on Automation and Logistics，Jinan，China，2007：2731～2735.

[3]Gonzalez-Vazquez S，Moreno-Valenz Uela J.A new nonlinear PI/PID controller for quadrotor posture regulation[C]//Electronics，Roboticsand AutomotiveMechanicsConference（CERMA）.Morelos，Mexico：IEEE，2010：642-647.

[4]刘一莎，杨晟萱，王伟.四旋翼飞行器的自抗扰飞行控制方法[J].控制理论与应用，2015，32（10）：1351-1360.

[5]于卫卫.三自由度四旋翼盘旋系统控制问题研究[D].辽宁：东北大学，2007.

[6]李杰，齐晓慧，韩帅涛.基于自抗扰技术的四旋翼姿态解耦控制方法[J].电光与控制，2013，20（3）：44-48．

[7]李毅，陈增强，刘忠信.自抗扰技术在四旋翼飞行姿态控制中的应用[J].哈尔滨工业大学学报，2014，46（3）：115-118.

[8]ZHOU Feng-yu，SHAN Jin-ming，WANG Wei，et al.Research on the design and simulation of a ship course controller based on ADRC[J].Joural of Shandong University，39（1）：57-62，76.

[9]韩京清.自抗扰控制技术-估计补偿不确定因素的控制技术[M].北京：国防工业出版社，2008.

[10]J.Q.Han.From PID technique to active disturbance rejection control technique[J].Control Engineering of China，2002，9（3）：13-18.2002.

[11]王俊生，马宏绪，蔡文澜，等.基于ADRC的小型四旋翼无人直升机控制方法研究[J].弹箭与制导学报，2008，28（3）：31-34.

[12]Z Chen，J Huang.Huang.Attitude tracking and disturbance rejection of rigid spacecraft by adaptive control[J].IEEE Transactions on Automatic Control，2009，54（3）：600-605.