基于模糊自适应脉宽调制的双反馈控制算法
2018-01-12,,
,,
(1.长安大学电子与控制工程学院,陕西 西安 710064;2.哈尔滨建成集团有限公司,黑龙江 哈尔滨 150030)
0 引言
进入新世纪,电力工业逐渐进入高速发展的新时代,对系统的控制在工业中扮演着重要的角色,稳定的系统控制在各种需要精确调节的工业部门中都有着极其重要的意义,比如航天、高精度生产线等。故可以看出,一种性能良好的控制系统对于工业发展等各个方面都有极大的作用。
控制系统的发展经历了若干发展阶段,其区分是依据控制原理不同,学术界一般认为开环控制系统是第一代控制系统。文献[1]将开环控制系统利用在尿素计量脉谱实验当中,阐述了根据开环控制系统来建模并验证其脉谱精度方法。由于开环系统不具有反馈环节,这就产生了明显的劣势,由于反馈的缺失,使得系统的性能如抑制干扰能力比较差,而且机械可调性也比较差。随后在吸收了开环的缺点后第二代采用单反馈控制系统,这种控制方式与开环系统相比具有较好的提升效果,在响应速度以及抑制干扰能力上都有着明显的提升。正如文献[2]、文献[3]所阐述的,该方法将反馈控制系统用在电机上,利用转速信号进行反馈,控制反馈电压与转速。这种控制方法虽然很好地解决了开环控制的一些显著缺点,但由于在单反馈控制下,系统仍然存在系统不易稳定等问题。因此在后来的发展中,学术界更加倾向于使用第三代控制,在第三代控制中提倡的是利用双反馈控制系统来提高稳定性能。文献[4]阐述了利用双反馈系统来提高单反馈控制系统的控制性能。采用这种改进的方法,可以解决第二代中的一些缺点,使其动态性能优于前者,但其超调过大且跟随误差较大,故该方法仍然存在一些缺点。
针对上述问题,本文提出了一种基于模糊自适应PWM的双反馈控制算法。
1 模糊自适应PWM双反馈控制算法基础
模糊自适应PWM双反馈控制算法的提出是建立在传统双反馈控制技术之上,通过把模糊自适应控制技术与PWM技术相结合的方式,实现了对双反馈系统高精度高鲁棒性的控制。
1.1 传统双反馈系统控制技术
传统双反馈控制系统结构如图1所示。在图中,ASR作为速度调节装置,ACR作为电流调节装置,与二者相连的GT是晶闸管触发电路,其作用为控制电压,速度调节装置与电流调节装置之间采用串联的方法连接,这样使得电流调节器作为内反馈,而速度调节器则为外反馈。内反馈的输入为外反馈的输出。而作为控制回路的末端的晶闸管触发器GT通过这样的控制回路最终得以生成整流电压Ud[5]。速度调节器所在的转速环对负载扰动起到抑制的作用,用于控制输入命令和输出转速之间的动态变化。电流调节器所在的电流环对电压扰动起到抑制的作用,用于控制电流随给定值的控制变化。两个调节器一般采用PI调节器。
1.2 模糊自适应控制技术
在简单的控制系统中,由于被控对象比较简单所以可以建立数学模型来进行控制。而在现实生活中,有太多因被控对象复杂而变得复杂的控制系统,对于这类系统,建立起精确的数学模型极为困难。在这种情况下,模糊自适应控制有了较为突出的优点,它不需要建立起精确的数学模型就可以进行高精度的系统控制。并且具有较强的灵活性和适应性[6]。
模糊自适应控制是根据给定的值r(t)和实际输出的值y(t)构成的控制偏差线性控制器。其偏差量为[7]:
e(t)=r(t)-y(t)
(1)
模糊自适应的数学形式控制规律为:
(2)
式中,K为采样序列,K=0,1,2…;u(k)为第k次采样时刻控制器的输出值;e(k)为第k次采样时刻输入的偏差值;ec(k)为第k次采样时刻输入偏差的变化值;Kp为比例系数;Ki为积分系数;Kd为微分系数。
模糊自适应控制是建立在常规控制基础之上的二元连续函数关系,它应用了模糊集合理论。其二次元连续函数关系为:
Kp=f1(|e|,|ec|),Ki=f2(|e|,|ec|),
Kd=f3(|e|,|ec|)
(3)
式中,|e|为偏差绝对值;|ec|为偏差变化绝对值;
1.3 PWM技术
PWM技术是通过把恒定直流电压调制成具有固定开关频率,且具有可灵活改变宽度的电压脉冲序列,从而可以改变负载两端的平均输出电压,得以调节直流电机转速的大小。
在此系统中,需按照某固定频率来使电压处在接通和断开的状态下,并且通过改变系统一周期内开关接通和断开的长短来使得电机的电压占空比发生变化,从而使得电机的转速得到控制。
占空比为系统开关导通时间与系统周期时间的比值,通过改变占空比ρ就可改变直流电机电枢的平均电压。而此系统电压系数为[8]:
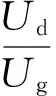
(4)
式中,Ug为由脉冲可调的脉冲电压;
当γ=2ρ-1时系统就为双极式可逆控制系统,其输出平均电压为:
(5)
式中,ton为开关导通时间;T为一个周期时间;Ua为电源以o为参考点的三相输出电压其中a端的输出电压。
2 模糊自适应PWM的双反馈控制算法的设计与实现
在本文所涉及的模糊自适应PWM的双反馈控制系统中,主控制系统主要由模糊控制器和PWM变换器和双反馈控制系统构成,而双反馈控制系统中最为关键的是电流调节器与电压调节器的设计。并且可以看出转速是调整系统平稳运行的关键所在,因此在控制系统设计时,将转速环节放在外侧,作为外环,而内环则使用需要相应很快的电流作为内环控制以抑制电网电压波动对转速的影响,再加上模糊控制器与PWM的配合可以得到很好的鲁棒性。
2.1 电流调节器设计
1)电流内环调节中,通常需要将时间常数首先确定,并忽略反电势的影响,将电流环中较小的系统合并因此可以得到电流环小时间常数之和为[9]:
TΣi=Toi+Ts
(6)
式中,Toi为电流给定滤波时间常数。
2)将控制对象函数化,将整体固有部分的传递函数简化可以表示为如下所示:
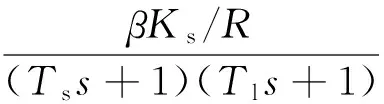
(7)
式(7)中,β被称为整个控制系统中的电流反馈系数;Ks为增益环节中的倍增系数;将控制系统内阻设定为R;电磁时间常数仍然使用Ti来表示;
简化后的电流环结构图2所示。
3)选择电流调节器结构
通常的控制系统设计要求σi≤5%,并在此情况下,尽量保证整个系统阶跃响应无稳态误差,因此可以按照自动控制理论中所提到的典型I型系统来设计电流内环的控制器。由于电流内环需要很快的响应速度,因此本文中选用PI控制器,PI控制器是PID控制器中当微分环节系数为零时的特殊情况,其具有很快的相应速度,比较常见于内环控制系统当中,再加上控制对象为双惯性环节,故其传递函数为[10]:

(8)
式中,Ki为电流调节器比例系数;τi为电调节器超前时间常数。
4)计算电流调节器参数
电流调节器超前时间常数为(其中Tl为系统控制参数,是已知):
τi=Tl
(9)
按照整个内环系统的开环增益要求,应取满足KITΣi=0.5,因此:
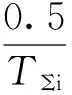
(10)
ACR的比例系数为:
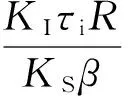
(11)
最终,经计算得电流调节器在MATLAB中建立的模型如图3所示。
2.2 转速调节器设计
1)转速外环的设计工作一般首先需要确定时间常数,转速外环的时间常数一般由两部分组成:电流环等效时间常数,转速环小时间常数,前者可以表示为[11]:
1/KI=2TΣi
(12)
转速环小时间常数计算公式为:
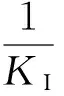
(13)
式中,Ton为转速给定滤波时间常数。
2)选择转速调节器结构
按照整个系统对于转速的要求,需要使用PI控制器,其传递函数为:
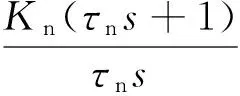
(14)
式(14)中,Kn即为转速调节器比例系数;转速外环的超前时间常数用τn表示。
3)计算转速调节器参数
为了使整个转速调节器具有较好的动态性能,对于外界干扰也具有相当的鲁棒性,故其超前时间常数具有如下限制关系:
τn=hTΣn
(15)
式(15)中为了达到设计要求的性能,需要设定h=5。
转速环开环增益为:
(16)
转速调节器比例系数为:
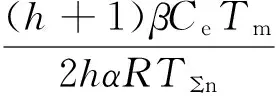
(17)
式中,Ce为电动机电势常数;Tm为机电时间常数;α为转速反馈系数;
最终,经计算后得转速调节器在Matlab中建立的模型如图4所示。
2.3 模糊自适应控制器的设计
在FIS图形窗口中建立两输入三输出的Mamdani推理模糊控制器。输入其论域与模糊规则语句,并选择相应的隶属度函数。图5为PID控制的3个参量(Kp,Ti,Td)的模糊控制规则。
2.4 模糊自适应PWM的双反馈控制算法系统的实现
通过Matlab中的Simulink软件,搭建基于模糊自适应PWM的双反馈控制算法的系统,仿真步长设定0.000 1 s,Power GUI中设定为离散。观察其实验结果。其步骤如下:
步骤1:根据所设计的模糊规则打开Matlab中FUZZY进行模糊规则语句的编写与模糊自适应控制器的搭建。
步骤2:对主电路电路进行设计。在Matlab中选择相关的元器件。
步骤3:通过式(6)-式(17)的电流调节器与转速调节器的参数计算,在Matlab中建立模型后放入控制回路。
步骤4:将模糊自适应PWM的双反馈控制算法系统与传统双反馈控制系统分别进行相连,将两系统电流环,转速环分别通过同一示波器进行连接,以便根据产生的图像来分析模糊自适应PWM的双反馈控制算法系统的性能。
步骤5:观察仿真结果,通过微调步骤3中的参数可以得出最佳的控制效果。
3 Matlab仿真与结果分析
3.1 Matlab仿真模型
如图6所示为最终得到的模糊自适应PWM的双反馈控制算法系统与传统双反馈系统对比Matlab仿真模型图。在图6中,Matlab中的两个待测装置分别具有四个合成信号输入口,其中所需要输入多的信号分别为角速度、电枢电流、电磁转矩。各个输出量在仿真时应设置单位一致。则要在产生角速度的支路上串接一个放大器并将其接到转速负反馈中,而将电枢电流Id接入电流负反馈中。
3.2 系统整体运行过程分析
系统搭建完后,点击运行按钮进行仿真,通过SCOPE原件可以得到模型的实时状态,系统的整个运行过程可以分为三个阶段。
在系统运行第一个阶段中系统启动时有很大的启动电流,启动转矩,ASR积分调节器的积分作用使得输入很大,给定电流在电流环调节作用下也增大,导致系统电流也增大,系统加速转矩,转速开始增大,但因电流此时还未增大到启动电流,所以系统转速几乎未增长。当电流增大到启动电流时,系统开始运转,ASR也很快到达限幅值,电流也很快上升,达到最大值;一定时间后整个仿真进入第二阶段,此时应为ASR控制器已经处于饱和状态,故转速环节相当于处于开环状态,这样的状态是十分危险的,系统此时在恒定电流给系统的调节系统供电,表现为电流不变拖动恒加速,整个转速呈线性增长。随后整个系统的转速达到待测装置的额定转速,此时转速调节器以及电流调节器多的反馈为零,系统进入第三个阶段,处于稳定状态。此时的转速调节器由于具有积分作用,使得转速持续地继续增加,出现超调使ASR再次出现负反馈,最后系统再次调节后处于稳定状态。
3.3 给定转速与反馈转速仿真结果分析
接下来设定给定转速进行仿真,以突显该方法对于传统的双反馈系统方法的优越性,其仿真结果如图7所示。图7上图为传统双反馈控制系统仿真结果,下图为模糊自适应PWM的双反馈控制算法系统。根据仿真结果可以分析出,转速外环是整个转速控制系统的主要控制装置,它的存在使转速很快能够跟随给定电压的变化,可以很大程度取消稳态误差的存在。传统双反馈控制系统中转速的超调量为5%,本文所采用的模糊自适应PWM的双反馈控制算法系统转速的超调量基本为零。传统双反馈控制系统中转速跟随性能不佳,不能做到无误差跟随,而模糊自适应PWM的双反馈控制算法系统转速跟随性能极好,可以做到无误差跟随。
3.4 给定电流与反馈电流比较仿真结果分析
通过图8采用给定电流与反馈电流之间的比较,可得出在转速外环的动态调整过程中,内环的作用只是为了使电压仅仅跟随外环的变化,而没有实质的调整作用。图8上图为传统双反馈控制系统仿真结果,下图为模糊自适应PWM的双反馈控制算法系统仿真结果。由图8可看出模糊自适应PWM的双反馈控制算法系统从运行开始就可做到无误差跟随,并且超调量极小。而传统双反馈控制系统初期出现较大程度的超调量,且0.5 s之后才实现无误差跟随。
4 结论
本文提出了模糊自适应PWM的双反馈控制算法。该算法通过模糊自适应控制器与PWM变换器相结合,对双反馈控制系统的转速实现了高精度高鲁棒性的控制。通过仿真实验表明,模糊自适应PWM的双反馈控制算法系统与前三代控制系统相比,可更好地抑制超调以及具有更小的跟随误差。
[1]刘传宝,颜伏伍,朱清山,等.柴油机SCR开环控制系统尿素计量脉谱标定方法[J].农业机械学报,2012,43(5):16-83.
[2]Pahlevani M,Eren S,Jain P. A hybrid estimator for active/reactive power control of single-phase distributed generation systems with energy storage[J]. IEEE Transactions on Power Electronics,2016,31(4):2919-2936.
[3]王强,王友仁,王岭,等.无位置传感器无刷直流电机闭环起动方法[J].电机与控制学报,2013,17(11):41-46.
[4]朱婵霞,胡敏强.并网故障下双馈感应风力发电系统的改进控制策略研究[J].太阳能学报,2014,35(3):449-455.
[5]王莉娜,朱鸿悦,杨宗军.永磁同步电动机调速系统PI控制器参数整定方法[J].电工技术学报,2014,29(5):104-117.
[6]杨帆,陈茂林,马新文,等.基于模糊PID算法的净化空调监控系统[J].华中科技大学学报(自然科学版),2014,42(1):120-123.
[7]朱雅光,金波,李伟.基于自适应-模糊控制的六足机器人单腿柔顺控制[J].浙江大学学报(工学版),2014,48(8):1419-1426.
[8]初亮,祁富伟,王彦波,等.汽车ABS电机PWM控制方法研究[J].华中科技大学学报(自然科学版),2014,42(10):58-62.
[9]周润,黄叙辉,张征宇,等.基于双闭环速度控制的捕获轨迹系统[J].航空学报,2014,35(6):1522-1528.
[10]Tir Zoheir, Malik Om P,Eltamaly Ali M.Fuzzy logic based speed control of indirect field oriented controlled double star induction motors connected in parallel to a single six-phase inverter supply[J].Elsevier B.V,2016(134):126-133.
[11]Puangdownreong D, Nawikavatan A, Thammarat C.Optimal design of I-PD controller for DC motor speed control system by Cuckoo search[J].Elsevier B.V,2016(86):83-86.
