基于自抗扰的机载激光武器跟踪控制系统设计

陈水忠， 刘 敏

(1.中国航空工业集团公司洛阳电光设备研究所，河南 洛阳 471000； 2.光电控制技术重点实验室，河南 洛阳 471000)

基于自抗扰的机载激光武器跟踪控制系统设计

陈水忠1， 刘 敏2

(1.中国航空工业集团公司洛阳电光设备研究所，河南 洛阳 471000； 2.光电控制技术重点实验室，河南 洛阳 471000)

通过对机载激光武器跟踪控制精度的需求分析，以典型激光通信电机模型为控制对象，选取了能够满足机载激光武器控制精度的复合轴控制结构和自抗扰控制算法，并结合工程实现，对控制参数整定进行了简化和改进，省去了跟踪微分器，将非线性的控制律和扩张观测器改为线性结构。实验结果表明，该设计方法能够满足粗、精瞄准阶段跟踪系统的角跟踪精度要求，且具有较强的灵活性和鲁棒性。

机载激光武器； 角跟踪控制； 自抗扰控制； 线性控制结构

0 引言

激光武器是一种利用高能量射束进行攻击的新概念武器，具有速度快、可控性强、连发能力好、杀伤力大等优点，适用于外科手术式的精确打击能力[1-2]，特别适于反卫星和破坏敌方信息系统，是未来高技术战争的新一代主战兵器。

由于激光武器的毁伤原理是要求激光能量在目标某个部位的能量累积，且激光光斑的远场半径一般为

自抗扰控制是采用“观测加补偿”的思想，基于传统PID 控制的原理，利用误差来消除误差，具有算法简单、实用性和鲁棒性强等特点，易于实现快速、高精度控制,非常适合于机载激光武器高精度角控制系统设计[4]。

1 机载激光武器控制精度需求分析

机载激光武器攻击过程的各个阶段对传感器的控制要求均不相同，在目标发现识别阶段要求传感器能够发现目标；在目标粗跟踪阶段要求传感器具备对目标的稳定跟踪能力；在目标精跟踪阶段要求传感器具备对目标攻击部位的稳定跟踪能力；在武器瞄准发射阶段要求武器持续稳定地照射在目标的某个部位，形成毁伤能量积累[5]。

1.1 目标相对信息计算

根据目标和激光武器载机的典型运动形式，计算相对几何关系，为后续性能计算提供数据。

根据目标和载机的位置坐标，计算其相对距离

(1)

式中：(xt,yt,zt)为目标在地面坐标系中的坐标；(xl,yl,zl)为载机在地面坐标系中的坐标。

根据目标和载机的速度，由相对视线的方位角和俯仰角，计算目标相对光学系统的速度。

(2)

式中：Vt为目标在地面坐标系中的速度；Vl为载机在地面坐标系中的速度；VRe为目标相对载机在地面坐标系中的速度；V相对光学系统为目标相对光学系统的速度；T(A,E)为由地面坐标系到视线坐标系的转换矩阵，A为视线方位角，E为视线高低角。

1.2 目标发现识别阶段光学系统参数计算

瞬时视场(IFOV)将受到单个探测元尺寸d的影响。IFOV就是焦平面上单个探测元所观察到的入射角范围。瞬时视场的算式为

(3)

式中：d为单个探测元尺寸；f为光学系统焦距。

根据物像比例关系，焦距可确定为

f=y′/y·D

(4)

式中：y′为目标在CCD靶面上所成像的大小；y为目标大小；D为目标到光学系统的距离。

焦距越长，目标所成像越大，越容易识别，但焦距过长，光学系统将过大。因此，按照成像的大小占两个像元作为系统识别的极限，即

y′=2d

。

(5)

光学系统像元分辨率是在其视场内区分为两个目标或一个目标各部分的能力。像元分辨率由目标距离和瞬时视场决定

ΔR=D×IIFOV

。

(6)

视场(FOV)为光电成像传感器所能收集的入射辐射的角范围，由透镜的焦距、像元尺寸和分辨率确定。水平方向的视场为

HFOV=NH×HIFOV

(7)

式中：NH为传感器水平方向像元个数；HIFOV为光学系统水平方向瞬时视场。

垂直方向的视场为

VFOV=NV×VIFOV

(8)

式中：NV为传感器垂直方向像元个数；VIFOV为光学系统垂直方向瞬时视场。

1.3 目标粗/精跟踪、瞄准阶段跟踪角精度要求

跟踪角精度是指传感器跟踪线和实际目标载机连线的角度差值，根据传感器和3σ要求，取传感器与目标首尾夹角的1/3为跟踪精度，则粗跟踪角精度的计算模型为

。

(9)

式中：e为目标进入角；L为目标的长度。

和粗跟踪阶段考虑的精度因素相同，需要把跟踪的范围由目标本身变为跟踪部位，由粗跟踪的模型推算精跟踪的模型，精跟踪角精度的计算模型为

。

(10)

式中,l为攻击部位的长度。

瞄准阶段是实现激光光斑持续照射在目标攻击部位的某一个点上，由于激光光斑的汇集半径很小(厘米级)，且激光具有光束到达的特点，所以该阶段需要考虑精度指标是瞄准角精度。

瞄准角精度是确保激光到达空中某点的能量超过90%，激光武器瞄准发射系统的瞄准精度应该为激光总的角发散量的1/3，即小于等于θa/3,θa为激光光束到靶发散角(锥体母线之间的夹角)。

2 机载激光武器角跟踪的自抗扰控制设计

为了达到微弧级的角跟踪控制要求，需要采用复合轴控制结构[6]，在二级控制回路中采用FSM实现对一级控制残差的补偿[7]，二级控制回路的控制算法由自抗扰控制技术决定。控制系统结构如图1所示。

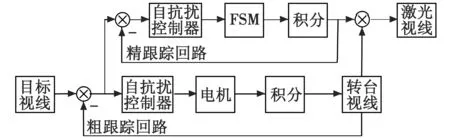
图1 基于自抗扰控制的复合轴跟瞄系统结构图Fig.1 ARDC based compound axis tracking- pointing system structure

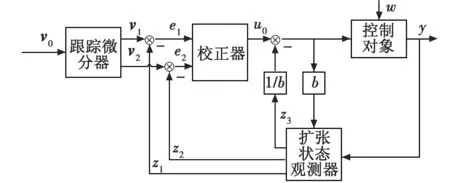
图2 自抗扰控制器的结构框图Fig.2 The structure of ARDC controller

自抗扰控制器包括跟踪微分器、扩张状态观测器和非线性校正环节[8]，图2所示为自抗扰控制器结构。 高精度粗跟踪系统多采用直流力矩电机驱动，与交流力矩电机相比，直流力矩电机控制特性好，力矩/惯量比较高、体积小，选取某典型激光通信的电机模型[9-10]，如图3所示。

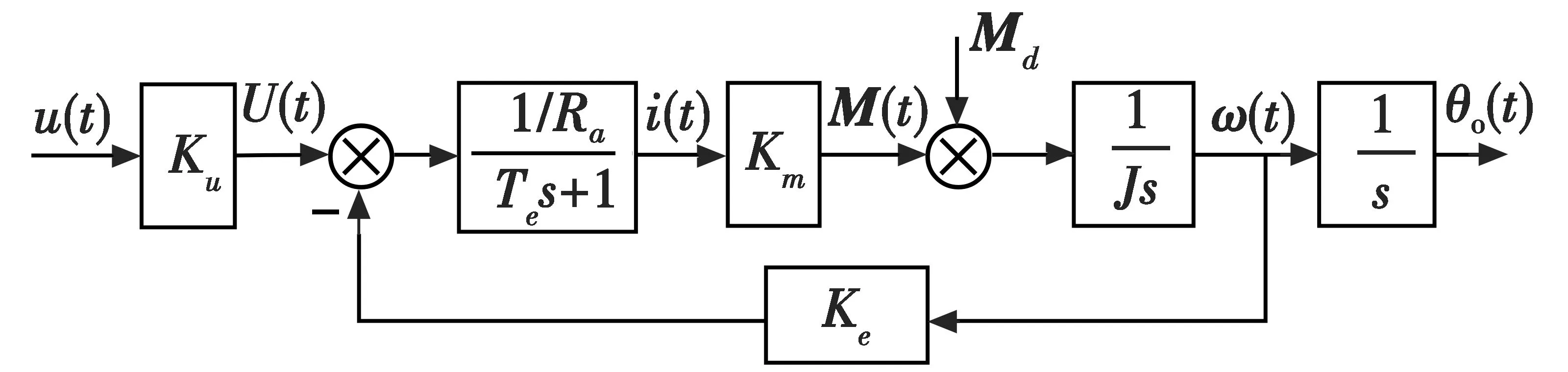
图3 直流电机模型Fig.3 DC motor model

图3中:u(t)为控制输入；U(t)为电枢绕组上的压降；i(t)为电枢电流；M(t)为作用在转台转轴上的主动力矩；Md为作用在转台转轴上的干扰力矩；ω(t)为电机转速；θo(t)为跟踪角度输出；Ku为功率放大器放大系数；Ra为电枢绕组电阻；Te=La/Ra为电机电磁时间常数,La为电枢绕组电感；Km为电机力矩系数；J为转轴上的转动惯量；Ke为电机反电势数。

忽略电机电感，则简化后的直流电机模型为二阶系统。通过对电机系统的模型辨识，获得电机模型的开环传递函数为

(11)

。

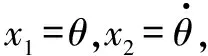
(12)

假设模型参数存在摄动，系统状态方程可进一步写为

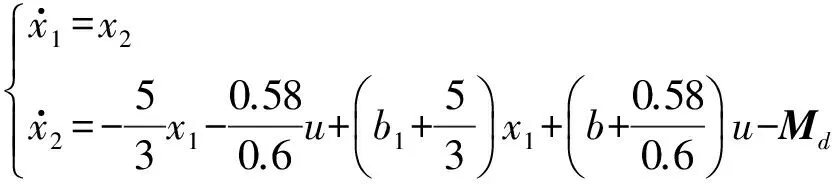
(13)

。

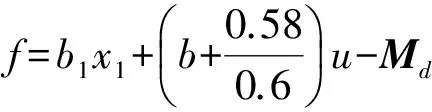
(14)

根据自抗扰控制设计原理，扩张后的被控对象可描述为

(15)

式中,L1为关于误差的非线性函数。取合适的L使得z1→x1，z2→x2，z3→x3。

设计控制量为：u=(u0-z3)/b，将其代入到系统状态方程中可得

(16)

。

(17)

首先，扩张状态观测器的引入将原系统转换为一个二阶积分系统，然后，可通过极点配置来设计控制律，从而使系统达到所期望的动态性能。

通常自抗扰控制器在信号输入端通过一个非线性跟踪微分器柔化输入信号，通过增加信号延迟减少突变导致的超调，同时在控制律和扩张观测器设计上引入非线性特性，以获得更好的控制效果[10-11]。但也存在所需设计参数众多、调整原则不明晰，与传统控制指标关系缺乏直观联系，不便于工程实现。为此，可做出如下简化和改进。

1) 自抗扰控制器实现跟踪控制时，如果要求具有极快的响应特性，而采用跟踪微分器会导致信号延迟，可在响应时间要求较高时，考虑省去跟踪微分器环节。

2) 将非线性的控制律和扩张观测器改为线性结构，这样可以减少参数调整个数，降低复杂程度，同时将参数设计与经典控制理论的频域、时域响应特性直接联系起来，便于根据实际系统需要进行选择设计。

由于电机模型简化为二阶系统，因此两自由度的比例微分控制器就可以实现极点的任意配置，引入线性控制律

(18)

式中：kp，kd分别为比例、微分增益;r为信号指令。

将上式代入式(9)，并转化为传递函数形式，有

。

(19)

由上式可知，经自抗扰控制器校正后，被控对象转化为一个典型的二阶系统。因此，通过引入阻尼因子和固有角频率可以确定kp，kd的大小，令

(20)

式中:ωc为固有频率；ξ为阻尼因子。

由二阶系统的响应特性可知，当ξ<1时，系统动态响应是欠阻尼的振荡特性；当ξ>1时，系统是过阻尼的单调特性；当ξ=1时，系统临界阻尼。在具体参数选择时，根据实际需要，如果要求系统无超调，可以选取较大的ξ值；而要求系统快速响应，可以选取较小的ξ值，一般取ξ为0.707。此时系统超调量较小，同时调节时间较短。由此确定

。

(21)

对于状态观测器采用线性形式

。

(22)

对于扩张观测器增益的选择，将上式转化为频域表达式，有

λ(s)=|sI-(A-LC)|=s3+L1s2+L2s+L3

(23)

引入参数ωo，使式(23)满足λ(s)=(s+ωo)3,那么，可以确定

。

(24)

上述方程将L增益矩阵的选择转换为ωo的选择，简化了问题的分析。ωo的大小反映了扩张观测器的带宽，其值越大，跟踪输入信号的能力就越强，但过高的ωo值也会引入更多的噪声干扰。因此要权衡选择。

在自抗扰控制器中，控制律的设计转换为ωc和ξ两个参数的选择，其中，ξ用来控制系统的超调量，ωc反映整个闭环控制系统的带宽，其大小可以根据需要的动态特性来选择，一般ωc<ωo。

另外还有参数b需要确定，一般在系统状态方程部分已知的情况下，可以选取b=b0，而从作用效果来看，b值相当于补偿作用因子，减小b值相当于增强补偿效果，但这不利于噪声的抑制，因此要在实际应用中调整确定。

3 仿真与分析

设定机载激光武器拦截无人机、弹道导弹和巡航导弹的典型场景，按照第1章计算角跟踪精度的模型，得到三种典型的跟踪精度要求，如表1所示。采用目标运动的等效控制信号作为验证控制效果的手段。

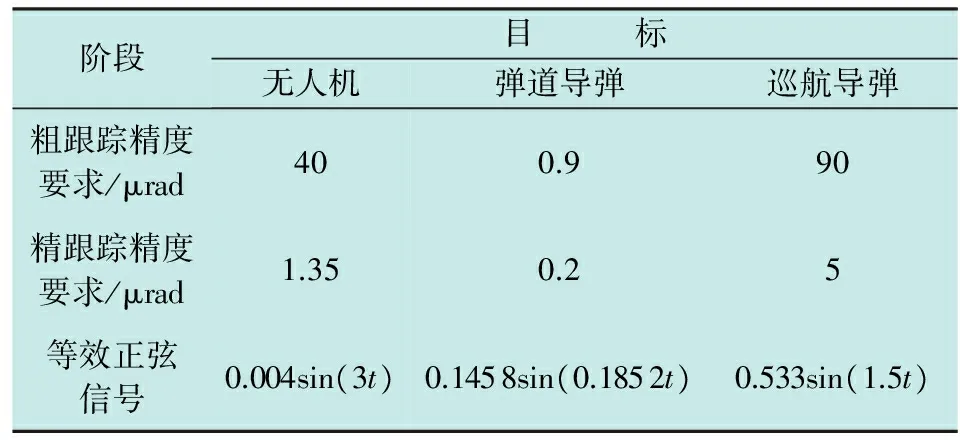
表1 三种典型目标跟瞄控制要求

以跟踪无人机的跟瞄控制要求作为设计依据，进行复合轴自抗扰控制系统设计，其中，粗跟踪自抗扰控制系统参数为：1) 扩张观测器参数：L1cu=300,L2cu=30 000,L3cu=1E7；2) 线性控制律参数：Kpcu=900,Kdcu=43。精跟踪自抗扰控制系统参数：1) 扩张观测器参数：L1cu=900,L2cu=2.7E5,L3cu=2.7E8；2) 线性控制律参数：Kpcu=1E4,Kdcu=146。

采用等效正弦信号对所设计的控制系统的效果进行验证，对无人机目标跟踪效果如图4所示。

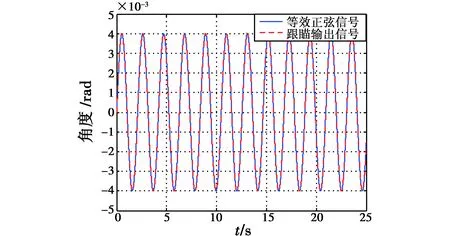
图4 无人机场景等效信号跟踪结果Fig.4 Equivalent sine signal of UAV tracking

由图5、图6可知，采用自抗扰控制后，粗跟踪精度为35 μrad，调节时间为0.025 s，稳态时间为0.11 s。精跟踪精度为0.23 μrad，调节时间为0.045 s，稳态时间为0.18 s。

图5 粗跟踪误差Fig.5 The coarse tracking phase error

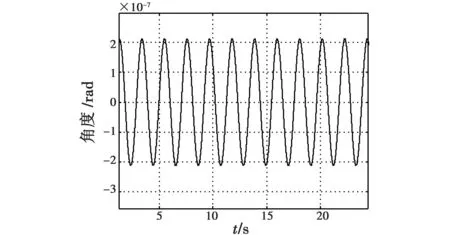
图6 精跟踪误差Fig.6 The fine tracking phases error

在粗跟踪回路输出端引入0.1sint的干扰噪声信号，同时对粗精回路电机主要参数进行50%放大，则粗跟踪电机模型变为

。

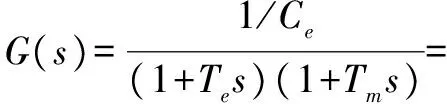
(25)

精跟踪电机模型变为

。

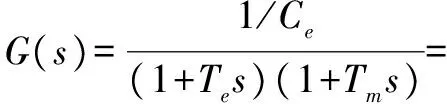
(26)

采用自抗扰控制系统跟瞄仿真结果见图7、图8。

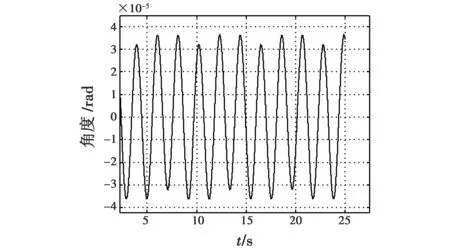
图7 干扰、参数摄动条件下自抗扰粗跟踪曲线Fig.7 The coarse tracking phase under parameter perturbation and disturbance

由图7、图8可知，在存在干扰和参数摄动时，粗跟踪精度大概为38 μrad，精跟踪精度为0.25 μrad。与理想情况下控制精度几乎一致，鲁棒性很强，体现了自抗扰控制采用扩张观测器后，可将未知扰动和参数摄动均作为未建模部分进行观测，加以补偿，使得控制参数适用范围大为提高，控制鲁棒性好。

与之前采用经典频域设计方法所设计控制系统对两者在相同条件下控制效果进行对比，结果如表2所示。

由表2可以看出，有无干扰和参数摄动对自抗扰控制系统的跟瞄效果影响很小，基本保持不变，鲁棒性很强。而采用经典设计的控制系统受干扰、摄动的影响较大，控制精度变差，干扰情况下的瞄准精度为1.8 μrad,大于要求的1.35 μrad，不满足控制精度要求。

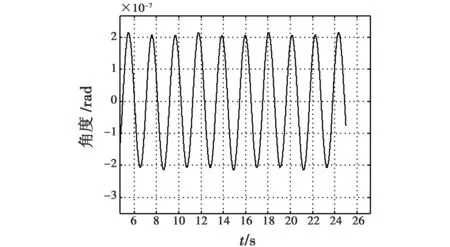
图8 干扰、参数摄动条件下自抗扰精跟踪曲线Fig.8 The fine tracking phase under parameter perturbation and disturbance

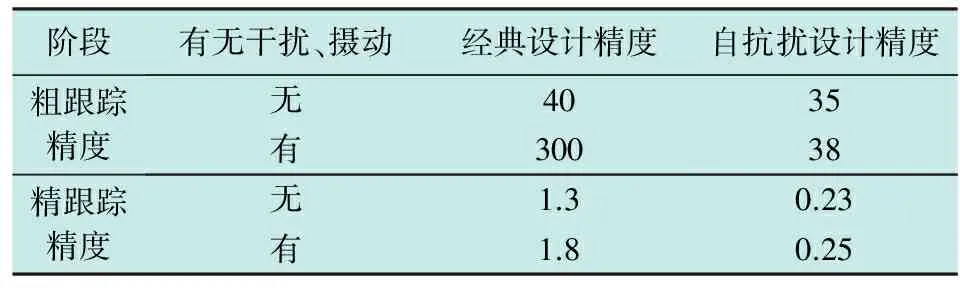
Table 2 Accuracy of two kinds of control systems μrad

4 结论

本文对机载激光武器传感器系统的跟踪控制需求进行了分析，构建了目标攻击过程火控各阶段传感器角精度要求模型，根据机载跟踪控制的特点选取自抗扰控制算法，结合跟踪系统电机模型对控制参数整定进行了简化和改进，并通过选取无人机目标的等效正弦信号对控制模型进行了有效性和正确性的验证，使机载角跟踪控制系统在满足精度要求的同时又具有一定的自适应性，与传统的控制方法相比，自抗扰控制方法参数整定简单，具有较好的动态性能，可提高机载激光武器控制系统的适应性和稳定性。后续，将进一步对所设计控制器抗干扰、参数摄动能力进行量化分析，对控制器参数整定方法进行研究。

[1] SPENCER J,CARAFANO J.The use of directed-energy weapons to protect critical infrastructure[R].Washington D C：Heritage Foundation,2004.

[2] ADAMS S,NAIRUS J.Energy conversion issues for airborne directed energy weapons[C]//Energy Conversion Engineering Conference,2004:61-64.

[3] 代志纲,岳巍澎,隋晓雨,等.自抗扰控制技术的原理剖析[J].新型工业化,2015(1):49-58.

[4] 邱晓波,窦丽华,单东升,等.光电跟踪系统自抗扰伺服控制器的设计[J].光学精密工程,2010,18(1):220-226.

[5] 黄勇,刘杰.高能激光武器的杀伤机理及主要特性分析[J].光学与光电技术,2004,2(5):20-23.

[6] 秦帅,张斌,李彬郎.模糊自抗扰控制在永磁同步电机调速系统的应用[J].计算机测量与控制,2014(10):3199-3202.

[7] 孙丽娜,宋悦铭,戴明.采用复合控制提高机载光电平台的数引跟踪精度[J].光学精密工程,2008,16(2)：265-269.

[8] 刘倩,谭文,李东海.一种多变量自抗扰控制结构的设计研究[J].华北电力大学学报:自然科学版,2014,41(6):97-103.

[9] 臧斌.直线伺服系统的基于参数优化自抗扰控制研究[D].沈阳:沈阳工业大学,2013.

[10] 段慧达.一类不确定高阶非线性系统的级联自抗扰控制策略研[D].长春:吉林大学,2012.

[11] 周宏,谭文.线性自抗扰控制的抗饱和补偿措施[J].控制理论与应用,2014,31(11):1457-1463.

TrackingControlSystemDesignforAirborneLaserWeaponBasedonActiveDisturbanceRejectionControl

CHEN Shui-zhong1, LIU Min2

(1.Luoyang Institute of Electro-Optical Equipment,AVIC,Luoyang 471000,China; 2.Science and Technology on Electro-Optic Control Laboratory,Luoyang 471000,China)

Analysis was made to the tracking accuracy requirements of airborne laser weapon.Taking a typical laser communication motor model as the object of control,a high-accuracy controller was designed by using compound-axis tracking control technology and active disturbance rejection control theory,which can satisfy accuracy requirement of airborne laser weapon.Then,combined with engineering practice,the controller was simplified and improved by omitting the tracking-differentiator and changing the nonlinear control law and extended state observer into linear structure.Simulation results show that the designed controller can satisfy the angle tracking accuracy of coarse and fine tracking phases,and exhibits good flexibility and strong robustness against external disturbance and parameter uncertainty．

airborne laser weapon; angle tracking control; active disturbance rejection control; linear control structure

陈水忠，刘敏.基于自抗扰的机载激光武器跟踪控制系统设计[J].电光与控制，2017，24(7)：85-89,99.CHEN S Z,LIU M.Tracking control system design for airborne laser weapon based on active disturbance rejection control[J].Electronics Optics & Control,2017,24(7):85-89,99.

V271.4

A

10.3969/j.issn.1671-637X.2017.07.018

2016-07-15

2016-08-21

陈水忠(1980 —),男，浙江诸暨人，硕士，高工，研究方向为系统工程。器系统的跟踪角精度要到达毫弧和微弧量级，传统的控制方法设计过程相对复杂，而且兼容性差，需要根据目标的运动特性、跟瞄精度要求调整控制参数[3]，并且在有干扰的情况下，控制效果会受到较大的影响，鲁棒性差。