一种全局稳定的四旋翼无人机移动目标跟踪控制
2018-01-11刘锦涛吴文海
刘锦涛, 高 丽, 吴文海, 汪 节, 辛 巧
(1.海军航空工程学院青岛校区,山东 青岛 266041; 2.伊犁师范学院数学与统计学院,新疆 伊宁 835000)
一种全局稳定的四旋翼无人机移动目标跟踪控制
刘锦涛1, 高 丽1, 吴文海1, 汪 节1, 辛 巧2
(1.海军航空工程学院青岛校区,山东 青岛 266041; 2.伊犁师范学院数学与统计学院,新疆 伊宁 835000)
针对地面目标机动不确定和风扰动条件下的四旋翼无人机目标跟踪问题,提出了一种全局稳定的控制策略。控制系统分为位置和姿态两个子系统。位置控制部分针对缺少目标与载机的相对速度问题,设计了输出有界的基于观测器的滑模控制器,且其输出能够保证所生成的期望姿态指令有界;设计了基于四元数的姿态控制器,通过增加非线性切换项,加快了动态跟踪速度,并得到了整个位置-姿态系统的稳定性证明。建立了风扰动模型,进行了目标机动情况下的跟踪飞行仿真,得到了满意的跟踪效果。
四旋翼无人机; 位置控制; 姿态控制; 目标跟踪
0 引言
当前,四旋翼无人机已经在军事侦察、航拍等很多领域得到了广泛应用,并进一步产生了能够跟踪移动目标自动飞行的新需求。
在四旋翼控制系统设计方面,由于它主要依靠垂直于机身的拉力推进,是一种欠驱动的非线性系统,为简化设计分析,可在四旋翼无人机非线性模型上分解成位置与姿态两个级联子系统,再分别进行控制器设计。近年来已成功研究出大量的姿态控制器和位置控
1 模型建立
1.1 四旋翼无人机运动模型
本文坐标系定义如下: {w1,w2,w3}为地理系(北东地);{b1,b2,b3}为机体系。如图1所示,b1,b2分别与四旋翼无人机的两轴重合,设b1为机头方向。第三轴b3与b1,b2满足右手定则。
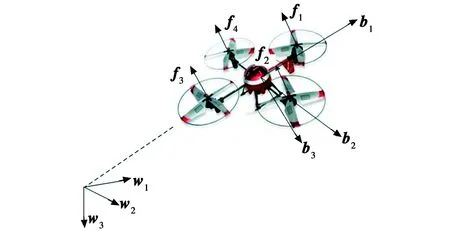
图1 四旋翼无人机模型Fig.1 Model of quadrotor UAV
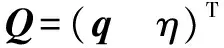
将力矩矢量M∈R3及拉力f作为系统的控制输入,四旋翼无人机的运动方程为
。
(1)
1.2 阵风模型
阵风采用文献[4]的“step”建模方法:连续的阵风由若干个风速不同的step组成,每一个step的风速的大小确定为
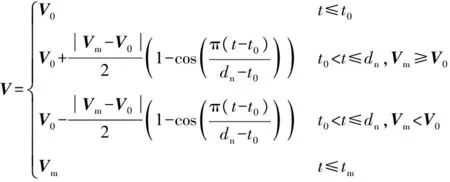
(2)
式中:V0是一个step开始的初始风速,也是上一个step结束时的风速;Vm是一个step结束时的风速;dn是此阵风上升时间;tm是此step的持续时间。
风的方向在一定范围内随机变化[5],即
ψw(n+1)=ψw(n)+Δψ
(3)
式中,Δψ为某个范围内的随机数,|Δψ|≤ψmax。
建立阵风的速度模型后,更重要的是计算阵风对四旋翼无人机的作用力,算式为[6]
Fw=SeAV2rel
(4)
式中:Se为有效影响面积;A=9.81/16=0.61为风速(m/s)2转换为压强(N/m2)的转换系数;Vrel,ψrel分别为无人机与空气(水平面上)的相对速度和方向,即空速和侧滑角,算式为
(5)
(6)
式中:vrelx=Vcosψw-vx;vrely=Vsinψw-vy。
由于四旋翼无人机所受的空气动力主要受旋翼的影响,因而可忽略机身的影响。将旋翼近似成一个圆柱体,如图2所示。

图2 姿态变化与旋翼的有效影响面积Fig.2 Quadrotor attitude and the effective area
圆柱的高度为桨叶的高度h,圆柱的半径为桨叶的半径r,α,β为旋翼的填充系数。风场对旋翼的作用面积受无人机的姿态影响,由俯仰角θ和倾斜角φ产生的迎风作用面分别为
Sex=βπr2sinθ+απrhcosθ
(7)
Sey=βπr2sinφ+απrhcosφ
(8)
则旋翼所受风的阻力在地理系下的分量形式为

(9)

(10)
则式(1)中的阵风扰动可写为
(11)
式中,μ为阻力系数。
2 问题描述
设机动目标:位置xd,速度vd,加速度ad。
(12)
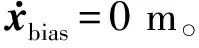
定义位置误差状态量为
(13)
(14)
定义姿态误差为
(15)
(16)
式中:Q和Qd分别为当前姿态和期望姿态的四元数表示形式;Ω和Ωd分别为当前角速度和期望的角速度。
位置部分:由式(13)和式(14)得到位置误差动态模型为
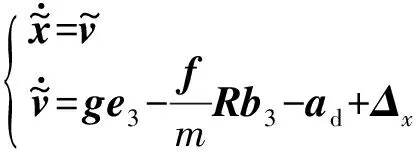
。
(17)
将目标机动加速度视为扰动进行处理,将不确定的扰动项合并为Δt=-ad+Δx。设u为位置控制器的虚拟指令[3],u=ge3-Rdb3f/m,则式(17)可改写为
(18)
设
h=f/m·(R-Rd)b3
(19)
(20)
则
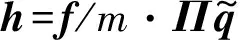
。
(21)
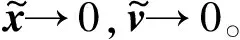
3 控制器设计及稳定性分析
3.1 总体设计思路
本文控制系统采用位置控制器和姿态控制器分离的结构,如图3所示,并在两者之间增加一个姿态指令提取环节,将位置控制器输出的平移加速度指令u转换为期望姿态Rd(t)和期望角速度Ωd(t)指令。
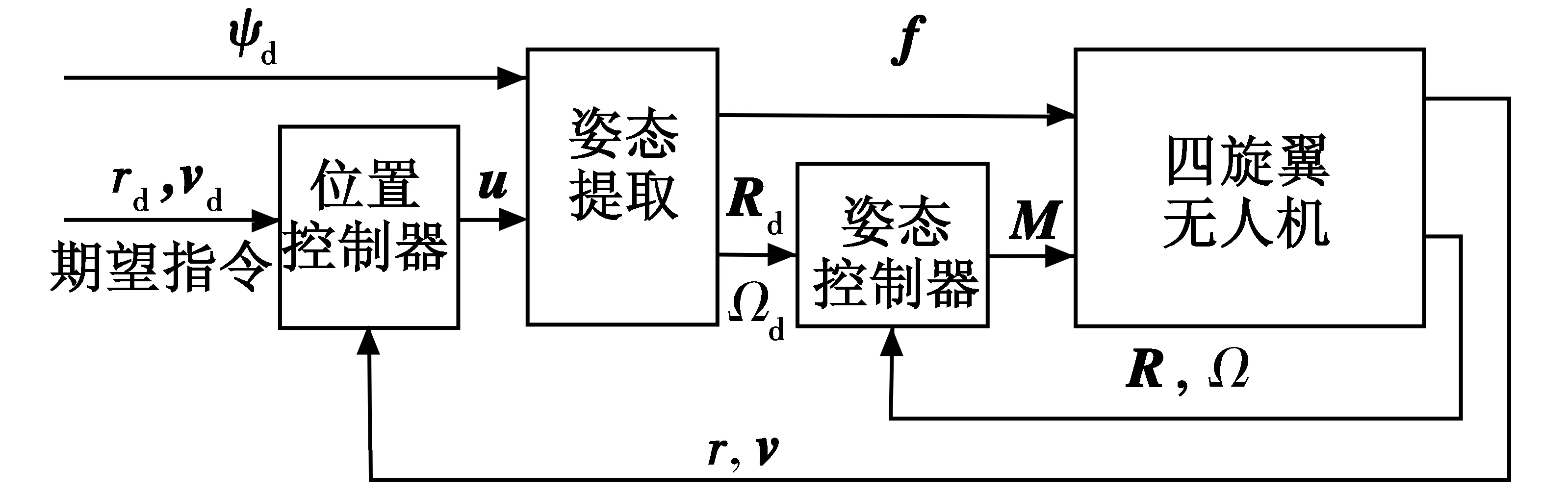
图3 四旋翼无人机控制系统结构图Fig.3 Structure of quadrotor UAV control system
3.2 期望姿态提取与指令约束
由位置控制器输出u合成期望姿态Rd。
设Fdes=m(ge3-u),由期望的升力矢量Fdes计算合力输出为
f=Fdes·Rb3
。
(22)
Fdes的方向即为机体轴期望的方向b3,des,有
。
(23)
设期望的偏航角为ψd,则
。
(24)

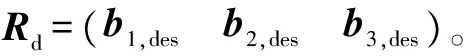
通过约束虚拟指令的u的范围,可实现对飞行器最大升降加速度及姿态角的约束要求。
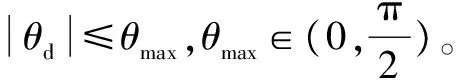
约束2(升降加速度):为避免自由落体运动,需要约束升降加速度小于重力加速度g,设|u3|≤amax,amax∈(0,g)。
当u=(u1u2u3)T满足式(25)约束条件时,则满足约束1和约束2:
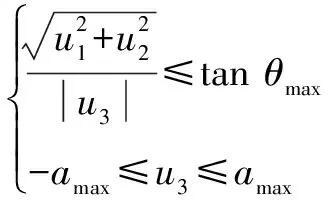
。
(25)
当升降加速度较小时,为简化分析,可将式(25)约束条件放宽,得到u的范围为
。
(26)
3.3 基于微分器的位置控制器设计
设计阶数为2的twisting控制器为
u=(u1u2u3)T
(27)
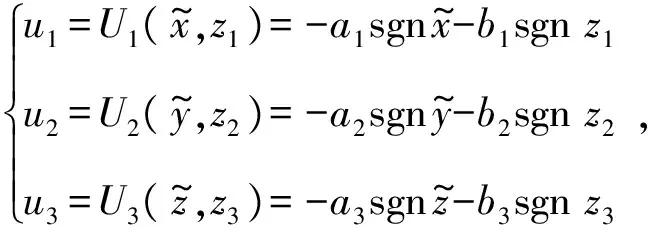
以控制器u1为例进行设计,u2,u3的设计方法相同。控制器参数取值范围为
。
(28)
此时则能够满足式(26)约束,进而满足姿态指令约束1和升降加速度指令约束2。
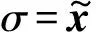
设初始条件:z0(0)=σ(0),z1(0)=0,则有
。
(29)
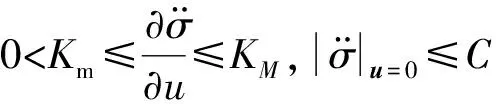

当存在测量误差时,估计误差也有界,且估计误差可随着L调整[7]。当测量噪声严重时,可考虑选取相对较大的L值,以获得更好的估计精度,但所造成的初始超调误差相对也会较大。
最终得到的控制器为
u1=U(σ,z1)=-a1sgnσ-b1sgnz1
。
(30)
参数取值范围

。
(31)
控制器参数a1,b1取值时要同时满足式(28)的上界条件以限制指令限幅,以及式(31)的下界条件式以保证系统稳定。控制器参数a2,b2,a3,b3值的选取方法同上。
3.4 姿态控制器设计

设
。
(32)
定义新的误差量
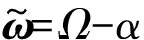
。
(33)
设计姿态控制器为
。
(34)
可得
。
(35)

令Ωd=0,则实际控制中所使用的控制器为
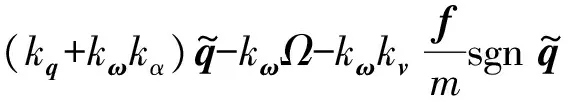
(36)
稳定性证明。
假设1扰动有界‖Δt‖2≤δt。
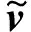
定理1当只有相对距离误差测量时,假设无测量误差,以及姿态控制器为式(34)的形式。若式(27)的位置控制器3个通道分别按照式(29)设计微分观测器及式(30)设计控制器;当kv≥4δv,b1≥δt时,系统是全局指数渐近稳定的。
证明考虑以下Lyapunov函数
(37)
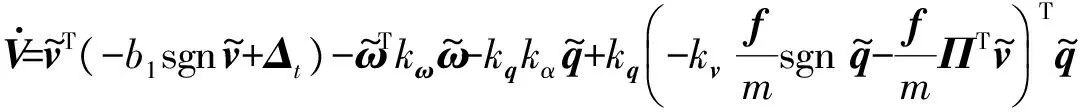
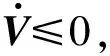
4 仿真
设四旋翼无人机质量m=0.45 kg,转动惯量J=trace(0.43×10-2,0.43×10-2,1.02×10-2),单位为kg·m2。
无人机初始状态设为零初(角速度、姿态、线速度、位置均为0)。期望位置希望保持在目标上方10 m处xbias=(00-10)T。为验证控制器的抗风扰动的性能,按照1.2节方式进行阵风仿真,tm={15 10152040},vm={0.513153}。速度与方向如图 4所示。
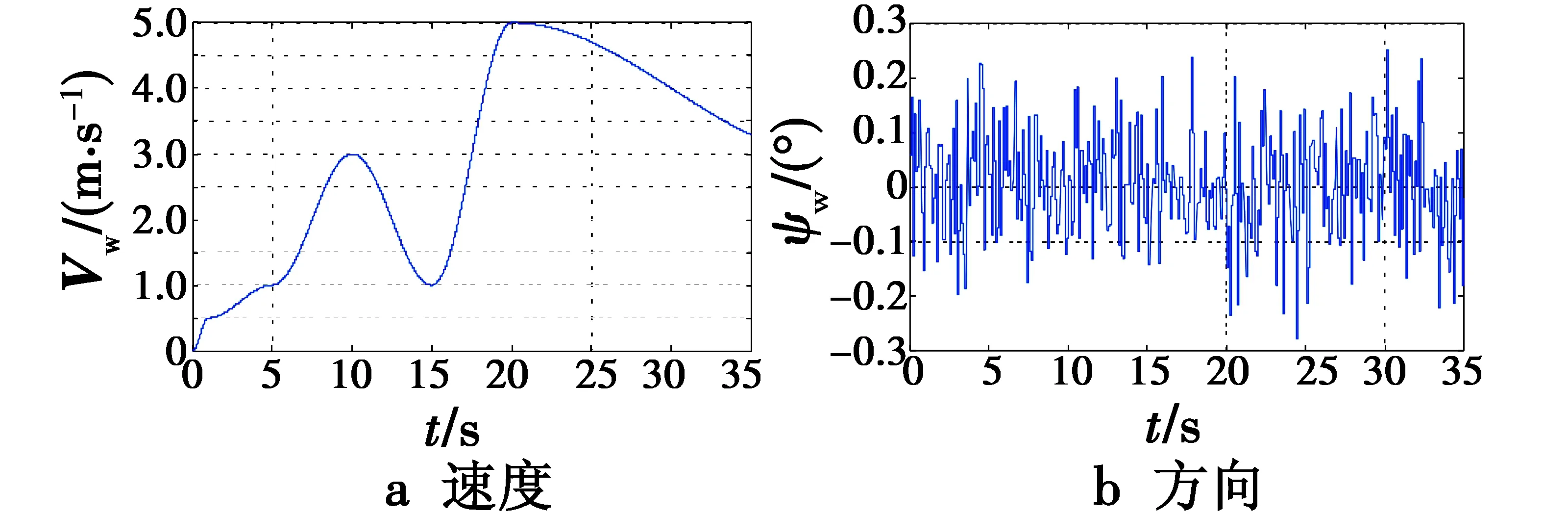
图4 阵风速度与方向变化Fig.4 Velocity and direction change of gust
仿真时长设为T=35 s,假设目标S形运动,速度大小为Vt=3 m/s。风扰动如图5所示。

图5 无人机所受风的扰动Fig.5 Disturbance force of wind on UAV
三维显示的期望轨迹与实际飞行轨迹如图 6所示。轨迹跟踪误差如图 7所示,能够迅速地实施跟踪,并将误差控制在较小的范围内。为便于对虚拟指令进行观察分析,采用欧拉角显示三轴的期望姿态角,如图 8所示,可发现生成的角度指令在10°以内。所生成的合力控制指令f如图 9所示,也在期望的范围内。相对速度的估计值和估计的误差分别如图 10、图 11所示,可发现在微分器初始建立阶段,相对速度估计误差较大,但能够在有限时间收敛,且估计效果不断变好。即便是存在风扰动情况下,无人机仍能实现机动目标的稳定跟踪。

图6 目标轨迹与飞行器轨迹Fig.6 Target trajectory vs vehicle trajectory
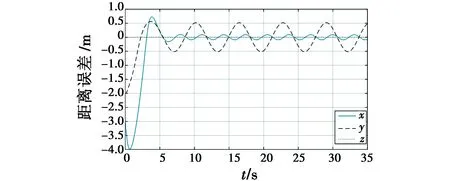
图7 轨迹跟踪误差Fig.7 Tracking error of trajectory
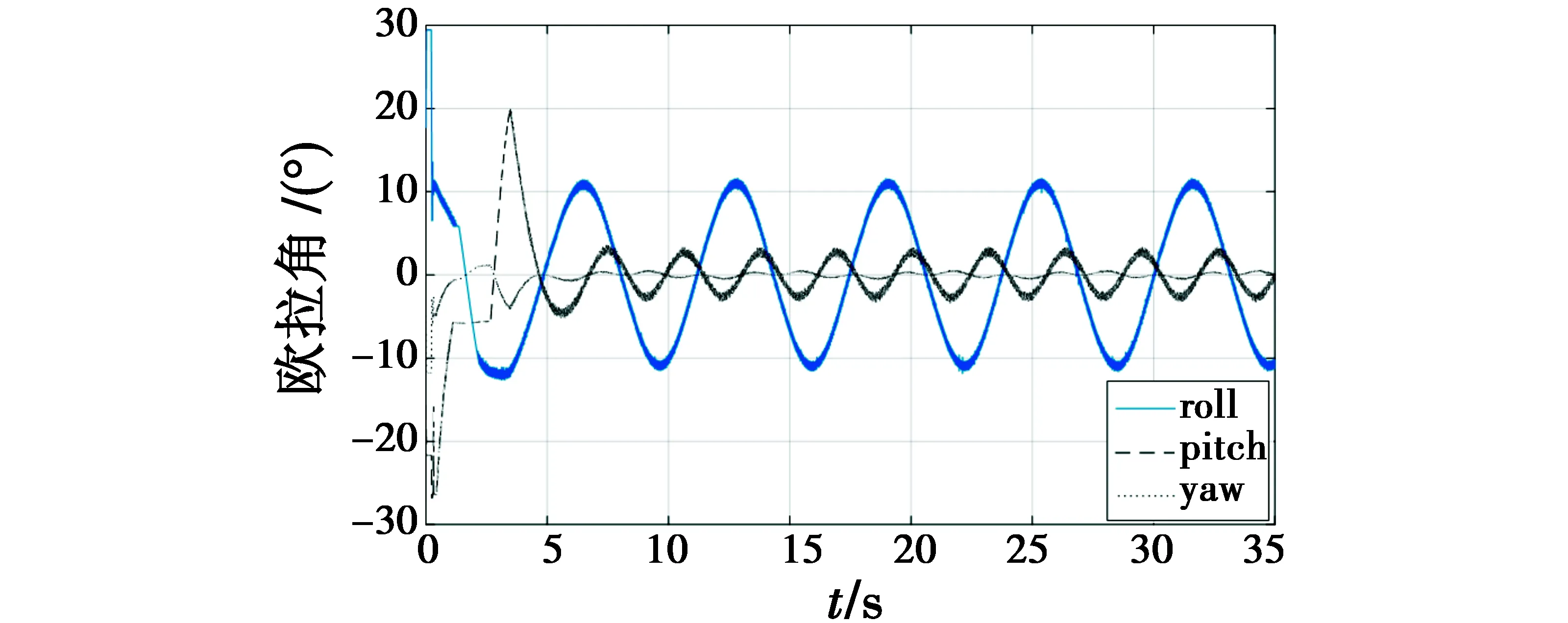
图8 期望欧拉姿态角Fig.8 Desired Euler angle of roll-pitch-yaw
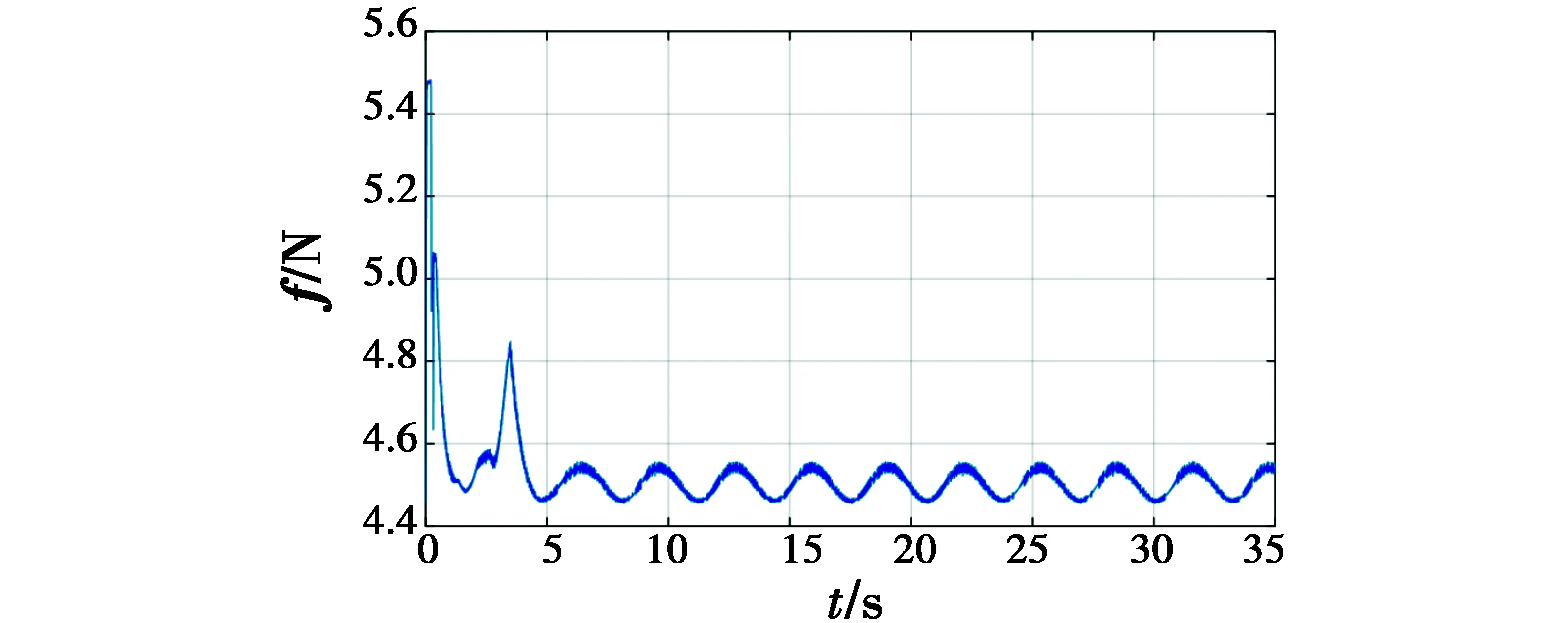
图9 f输出Fig.9 Output of command f

图10 相对速度估计Fig.10 Estimation of relative velocity

图11 相对速度估计误差Fig.11 Estimation error of relative velocity
5 结论
本文通过将四旋翼无人机非线性模型分解成位置与姿态两个级联子系统,简化了设计分析。
设计了一种位置-姿态控制器,通过super-twisting微分器估计相对速度信息,且位置控制器所生成的期望姿态指令在指定的范围内,并设计了相应的保证全局稳定的姿态控制器。
通过仿真试验表明,当无人机倾斜姿态较小时,风场干扰力较小,而基于微分估计器的位置控制器生成的姿态指令有界,通过适当参数选取能够避免出现较大的姿态角指令,由于姿态控制器中引入了与拉力指令f相关的鲁棒项,提升了跟踪速度,且动态性能良好,整个位置-姿态系统得到了全局指数渐近稳定的证明,可应用于类似的欠驱动系统的运动控制。
[1] RAFFO G V,ORTEGA M G,RUBIO F R.An integral predictive/nonlinearH-infinity control structure for a quadro-tor helicopter[J].Automatica,2010,46(46):29-39.
[2] MADANI T,BENALLEGUE A.Sliding mode observer and backstepping control for a quadrotor unmanned aerial vehicles[C]//American Control Conference,2007:5887-5892.
[3] ABDESSAMEUD A,TAYEBI A.Motion coordination for VTOL unmanned aerial vehicles:attitude synchronisation and formation control[M].Berlin:Springer Science & Business Media,2013.
[4] PSHIHOPOV V H,Y,MEDEVEDEV M,GAYDUK A R,et al.System of position trajectory control of robot-aided aeronautical platform.Part 1.Mathematical model[J].Mechatronics,Automatization Control,2013(6):14-21.
[5] SIDOROV V V.Meteorology and climatology:study guide[M].Ekaterinburg:GOU SPO UGTU-UPI,2006.
[6] PODOBED V A.Mathematical simulation of wind force over quaternion crane[J].MGTU Herald,2006,9(2):318-331.
[7] LEVANT A.Universal output-feedback SISO controllers[J].Asian Journal of Control,2003,5(4):484-497.
AGlobalStableQuad-rotorUAVControlforTrackingMovingTarget
LIU Jin-tao1, GAO Li1, WU Wen-hai1, WANG Jie1, XIN Qiao2
(1.Naval Aeronautical Engineering Institute Qingdao Branch,Qingdao 266041,China; 2.College of Mathematics and Statistics,Yili Normal University,Yining 835000,China)
For tracking the ground target with unknown maneuvering under gust disturbance,a global stable control policy is proposed for quad-rotor UAV.The control system is divided into position and attitude subsystems.In position subsystem,to the problem of no relative velocity measurement between the target and UAV,a bounded-output sliding mode position controller with observer is designed,which command outputs are in the specified range.The corresponding quaternion attitude controller is designed by using nonlinear switch term to achieve fast convergence.Therefore,the global stability property of the whole position-attitude system is achieved.Finally,the gust is modeled and the simulations of maneuvering target tracking missions show satisfactory tracking performance even in the wind field.
quad-rotor UAV; position control; attitude control; target tracking
刘锦涛,高丽,吴文海,等.一种全局稳定的四旋翼无人机移动目标跟踪控制[J].电光与控制,2017,24(7):52-56,61.LIU J T,GAO L,WU W H,et al.A global stable quad-rotor UAV control for tracking moving target[J].Electronics Optics & Control,2017,24(7):52-56,61.
TP13
A
10.3969/j.issn.1671-637X.2017.07.011
2016-07-08
2017-04-07
国家自然科学基金(11461075)
刘锦涛(1981 —),男,山东莱阳人,博士生,工程师,研究方向为无人机导航与控制。制器。如RAFFO等人提出了一种积分预测非线性鲁棒控制器[1];MADANI等人提出基于滑模观测器和backstepping方法的轨迹跟踪控制器[2]。但大量类似的设计普遍缺乏级联系统全局稳定的证明。针对此问题,文献[3]设计的四旋翼跟踪控制律得到了全局有界性和收敛性的结果,但未考虑外部干扰的影响。本文针对阵风和目标机动的干扰,以及缺乏速度反馈等问题,设计了一种位置-姿态控制器,位置控制器设计了一种基于速度估计器的twisting控制器,能保证所生成的期望姿态指令在指定的范围内,并设计了相应的姿态控制器。整个位置-姿态对外部扰动和模型不确定性具有较好的鲁棒性,且得到了全局有界性和收敛性的证明。最后进行了针对机动目标的跟踪飞行仿真,并增加了风扰动,最终得到了满意的仿真结果。
