弹道导弹微动特征散射点的选取

张 瑜, 赵小纳, 王召迎

(1.河南师范大学电子与电气工程学院，河南 新乡 453007;2.河南省高等学校电磁波特征信息探测重点学科开放实验室，河南 新乡 453007)

弹道导弹微动特征散射点的选取

张 瑜1,2, 赵小纳1, 王召迎1

(1.河南师范大学电子与电气工程学院，河南 新乡 453007;2.河南省高等学校电磁波特征信息探测重点学科开放实验室，河南 新乡 453007)

目标识别； 弹道导弹； 微多普勒特征； 特征参数； 散射点

0 引言

随着现代战争要求的精准探测和打击，作为现代雷达重要发展方向的目标识别技术越显重要，也一直是雷达领域中的研究热点。弹道导弹的识别是其防御系统中的核心技术，其识别的精准程度可能决定反导系统的成败[1]。弹道导弹在飞行过程中，除了主体移动外，还会有进动、章动等微小运动(称为微动)，它属于目标的精细特征。雷达探测目标时除了可在回波信号中得到因主体运动产生的多普勒频率外，还会得到因微动产生的附加频率调制，即在主体运动的多普勒移频附近产生边频，这种附加的多普勒调制称为微多普勒效应[2]。

由于目标运动的微动特征是其特有的表现形式，因此可利用微多普勒效应进行雷达目标识别。目前，基于微多普勒效应的目标识别技术被认为是雷达目标识别领域中最具潜力的技术途径之一，国内外众多学者在此方面进行了许多深入研究，取得了较多的科研成果[3-4]。在利用微多普勒效应进行目标识别中，多种信号分析方法被采用，其中最常用的有时频分析法、频谱与倒谱法和延时共轭法。获得微多普勒频率的关键是对雷达回波信号瞬时频率的高精度估计和提取。由于目标微动具有时变性，雷达微多普勒回波也具有时变性和非平稳性，因此能够同时对时间和频率进行分析的时频分析法成为基于微多普勒的雷达目标识别技术中的主要分析方法[5]。

在基于微多普勒的弹道导弹微动特征参数提取中，国内一些大学做了大量相关工作，得出了许多有益的成果[6-10]。在弹道导弹微动参数提取中，需要在目标上选择散射点，而散射点位置、个数的变化可能会影响微动参数的提取精度，进而影响对目标的识别效果。

弹头在自旋定向时，会产生进动和章动等微动特征；脱离物没有姿态控制系统，会呈现出翻滚或者摇摆等姿态；弹头质量较重，其自旋频率通常为2 Hz，对于脱离物则质地较轻，其自旋频率通常要达到8 Hz左右，脱离物的微动特性与真弹头的微动特性存在明显差异，因此，只要找取合理的散射点位置进而提取弹道导弹的微动特征参数便可以明显地区分出脱离物与弹头。鉴于目前对该类研究还很少，本文利用时频分析法研究弹道导弹的微动参数提取效果随散射点位置、个数的变化规律，以便为实际应用中的散射点选择提供帮助。

1 弹道导弹目标运动模型与微动特征参数提取方法

弹道导弹的弹头大都是锥体，在中段飞行时不仅平动飞行，通常还伴随着进动形式的微动，即不仅具有绕自身对称轴的旋转，还有绕其锥旋轴的旋转，弹头的进动如图1所示。设弹头的自旋轴为Z轴，进动角为θ，则锥旋轴为(0 sinθcosθ)，自旋角频率为ωs，锥旋角频率为ωc。再假设雷达位于R0处，雷达视线与Z轴夹角为φ，则雷达视角单位矢量rLOS=(0 sinφcosφ)。

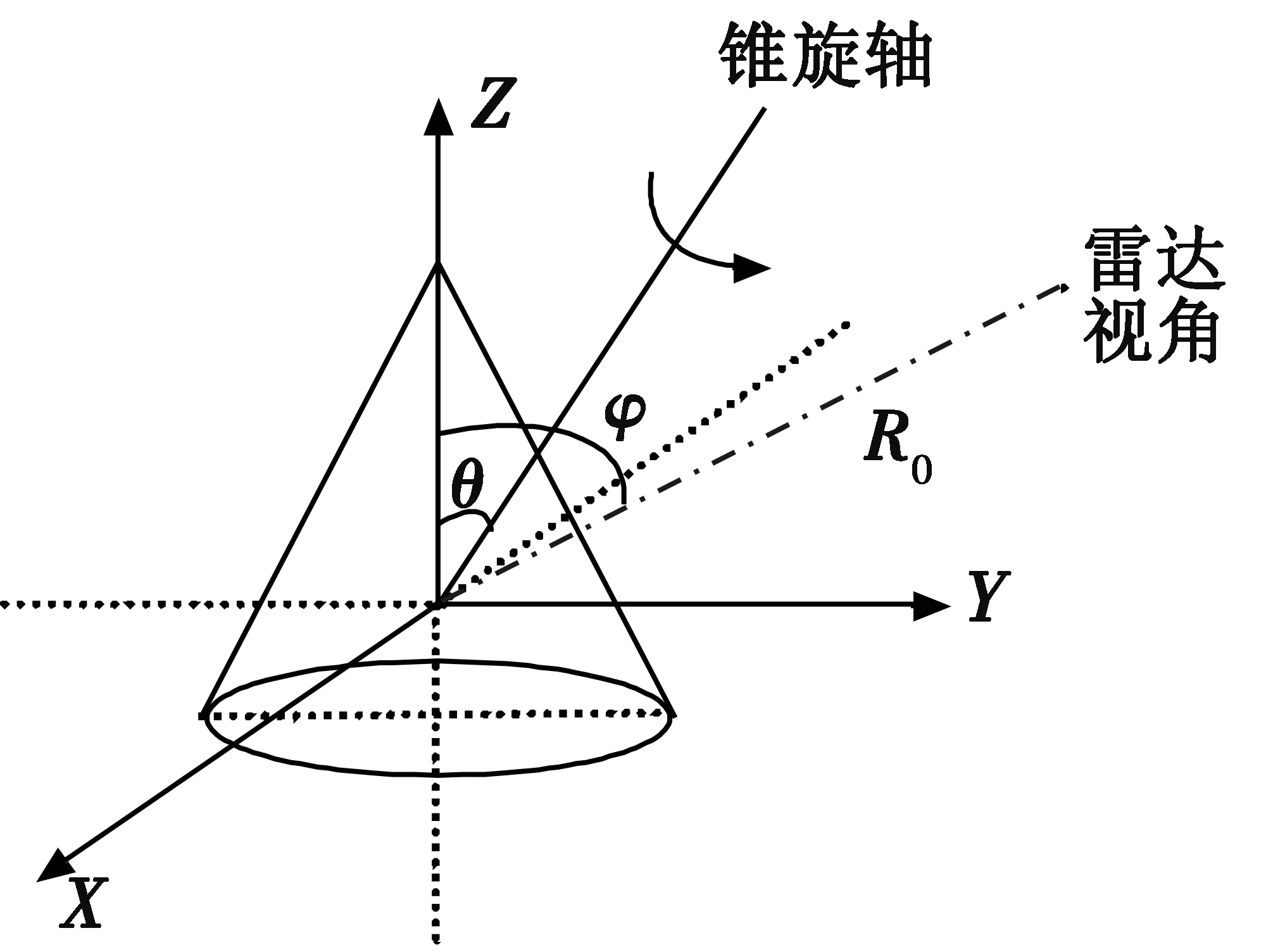
图1 弹头进动示意图Fig.1 Warhead precession diagram

假设导弹弹头表面上任一散射点i的初始位置坐标为(x0y0z0)T，一段时间t后，i点的位置坐标变为ri(t)=(xtytzt)T，则有

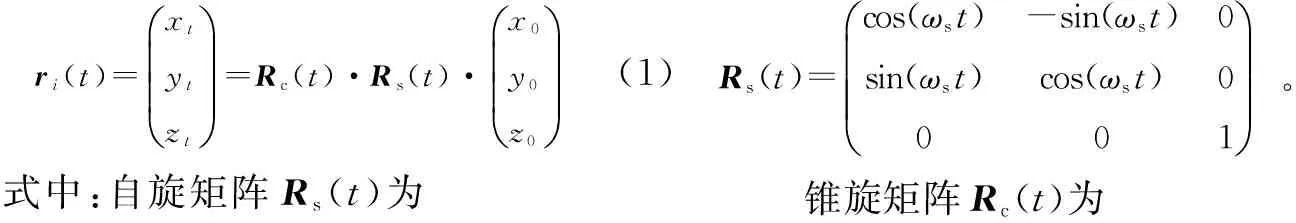
ri(t)=xtytztæèççöø÷÷=Rc(t)·Rs(t)·x0y0z0æèççöø÷÷(1)式中:自旋矩阵Rs(t)为Rs(t)=cos(ωst)-sin(ωst)0sin(ωst)cos(ωst)0001æèçççöø÷÷÷。锥旋矩阵Rc(t)为

目标散射点i到雷达的径向距离为

R(t)=R0-(ri(t),rLOS)

(2)

式中:(ri(t),rLOS)为ri(t)与rLOS的内积。这样有(ri(t),rLOS)=[-sin(θ-φ)sin(ωct)cos(ωct)+(cos(1-cos(ωct))sin(θ-φ)+sinφ)·sin(ωst)]x0+sin(θ-φ)sin(ωct)·sin(ωst)+(cosθ(1-cos(ωct))·sin(θ-φ)+sinφ)cos(ωst)y0+[sinθ(1-cos(ωct))sin(φ-θ)+cosφ]z0。

(3)

当雷达发射载频为fc的单频连续波信号时，锥形弹头微动的雷达回波信号为

(4)

式中,ρi为散射点i的回波强度。

由式(3)、式(4)可见，散射点i的瞬时位置为自旋频率、锥旋频率、进动角与雷达视线角之差的正弦函数的线性叠加。如果能够提取到散射点的瞬时位置变化则就可利用式(4)对弹头微动的雷达回波信号通过短时傅里叶变换进行时频分析[11]，从而得到弹头目标的进动频率，即自旋角频率ωs和锥旋角频率ωc。

2 弹道导弹目标散射点的选取

对大多数弹道导弹而言，平底锥形尖端是其弹头的一个普遍特征，散射点只能分布在锥形尖端、锥形底部和锥形面上，因此这里主要分为4类情况选择散射点位置，如图2所示。第1类是散射点在锥形尖端，由于尖端很小，因此这种情形只选择1个散射点，如图2a所示；第2类是散射点在锥形底部选择散射点，由于锥形尖端是1个特殊的点，因此这类情形锥形尖端选择1个散射点，在锥形底部分别选择2,4,8,20个散射点，如图2b所示；第3类是散射点在锥形面上选择散射点，除了在锥形尖端选择1个散射点，在锥形底部对称选择2个散射点外，在锥形面上分别随机选择2,4,15,20个散射点，如图2c所示；第4类是特殊情形，只在锥形面上随机选择30个散射点，如图2d所示。

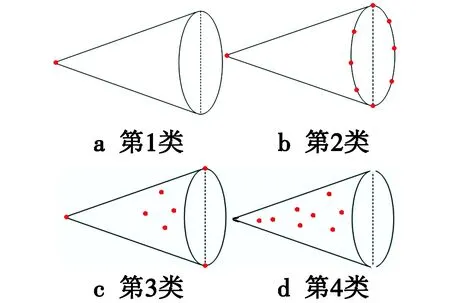
图2 散射点选择示意图Fig.2 Scattering point selection

3 微动特征参数随散射点变化的仿真与分析

仿真参数选取：雷达发射C波段的单频信号，频率为fc=5 GHz，脉冲重频为4000 Hz，θ=30°，φ= 60°，自旋频率5 Hz，锥旋频率2 Hz。

3.1 第1类散射点分布

设定1个散射点且位于弹道导弹尖端，位置坐标为P0=(0,0,1)。利用式(4)得到的信号进行时频分析，可仿真得到该情形的时频分析结果，如图3所示。

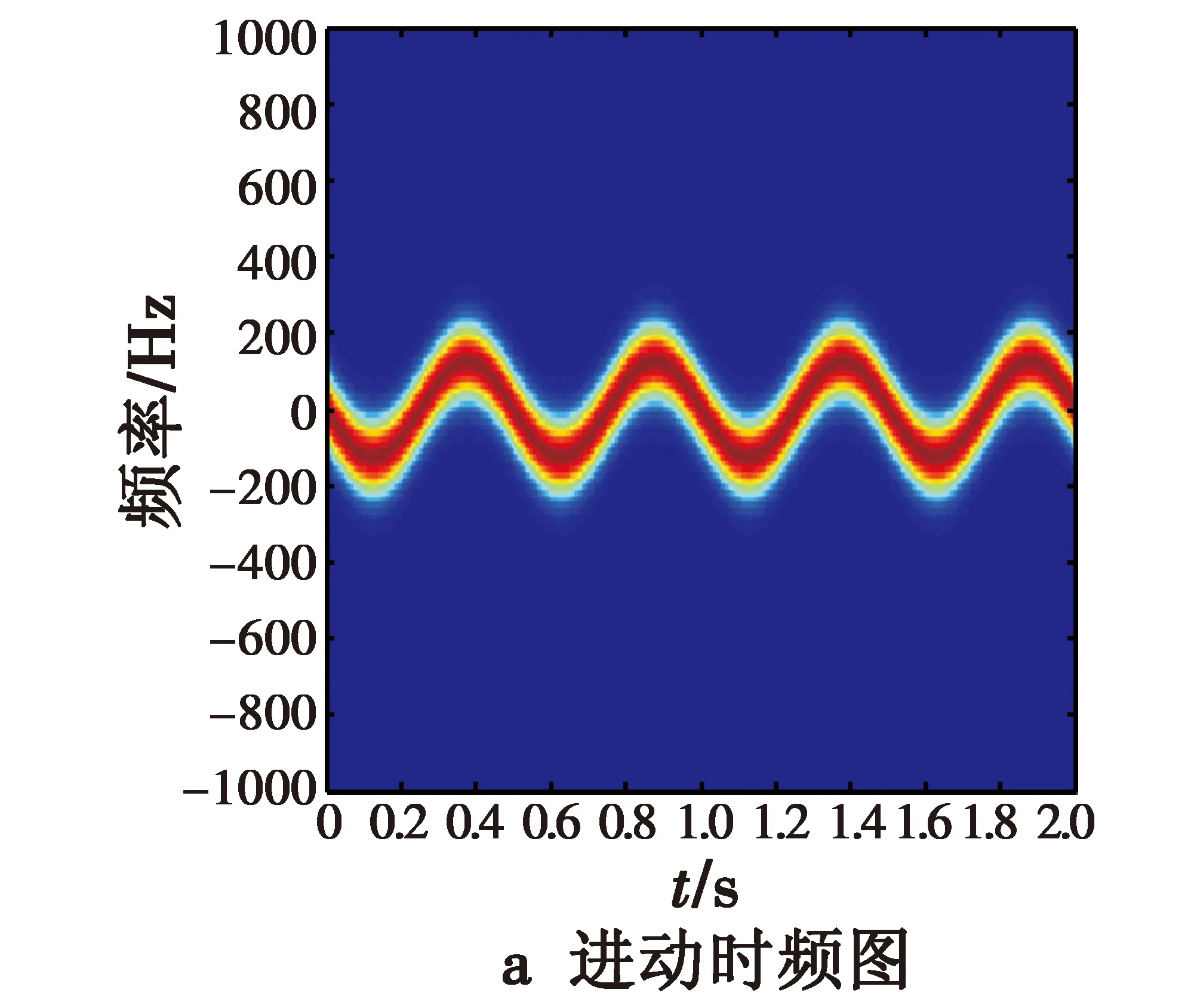
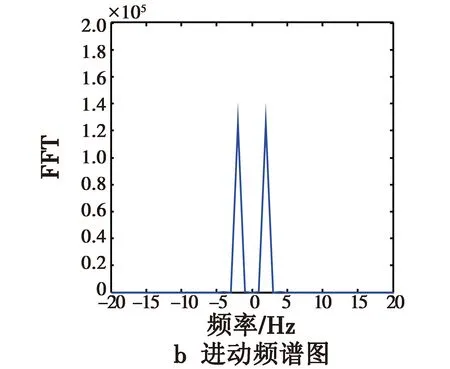
图3 单一散射点时的仿真结果Fig.3 Simulation results for a single scattering point

图3a为1个散射点的弹头目标的进动时频图，显示了该散射点的瞬时多普勒频率随时间的分布特性。由于散射点位置特殊，刚好位于自旋轴上，微动特征就仅包含锥旋，此时对应的微多普勒频率随时间的变化曲线为正弦曲线形式。

图3b为1个散射点的弹头目标的进动频谱图。从图中可以明显看出频率轴上的2个强的频率值,即2 Hz和-2 Hz，这也正是需要提取出的频率分量——锥旋频率，这说明在弹头的圆锥尖端选择1个散射点可以很好地得到导弹微动的锥旋参数。

3.2 第2类散射点分布

此类实验分别选取3,5,9,21个散射点，其中,1个在弹头的锥形尖端，位置坐标为P0=(0,0,1)，其余的散射点对称地位于弹头的锥形底部边沿或随机分布在锥形底部。通过利用式(4)得到的信号进行时频分析，可仿真得到对应各种情形的时频分析结果。弹头的锥形底部边沿对称地分布2,4,8个散射点和在锥形底部随机分布20个散射点时的进动时频图如图4所示，通过傅里叶变换得到的对应进动频谱图如图5所示。

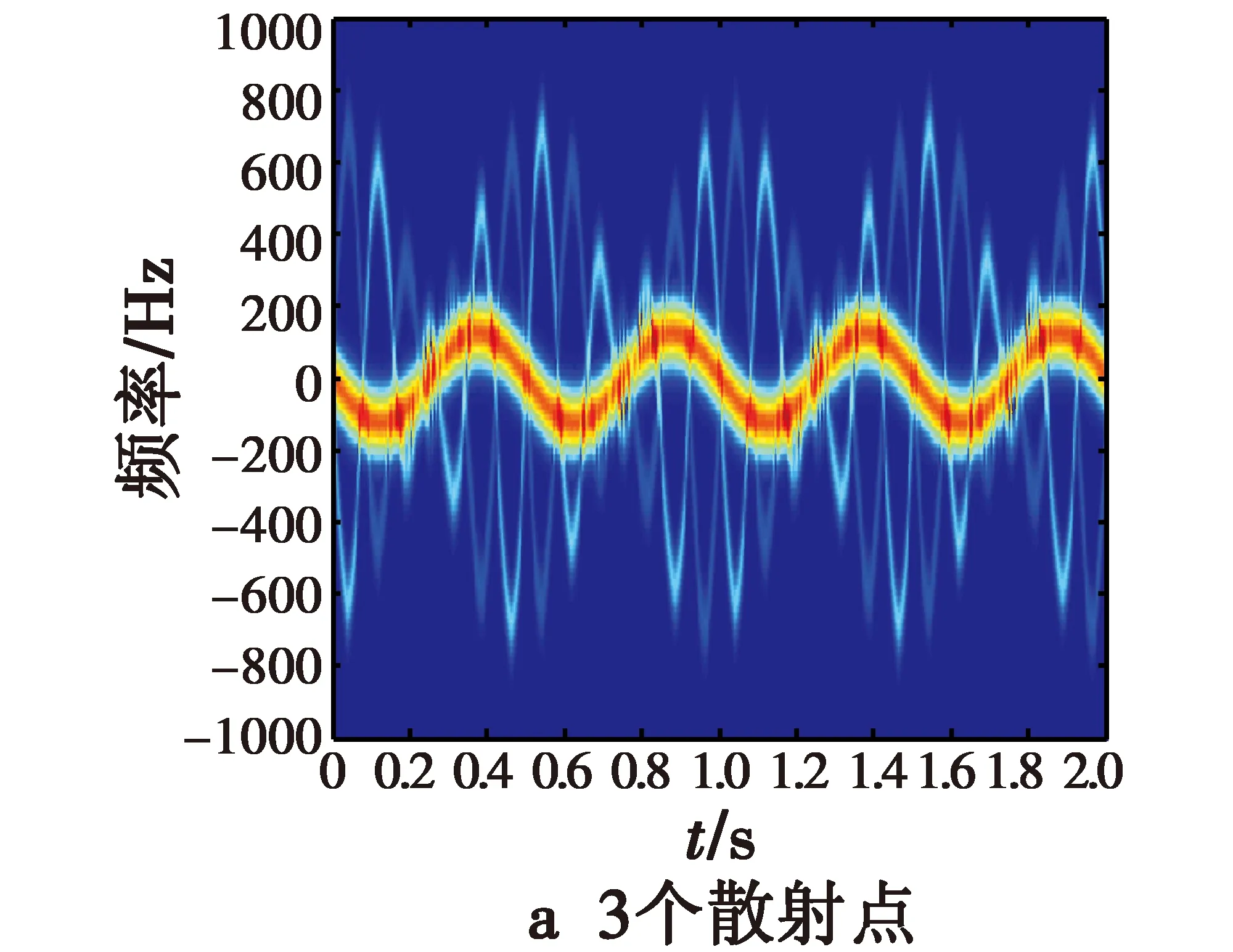
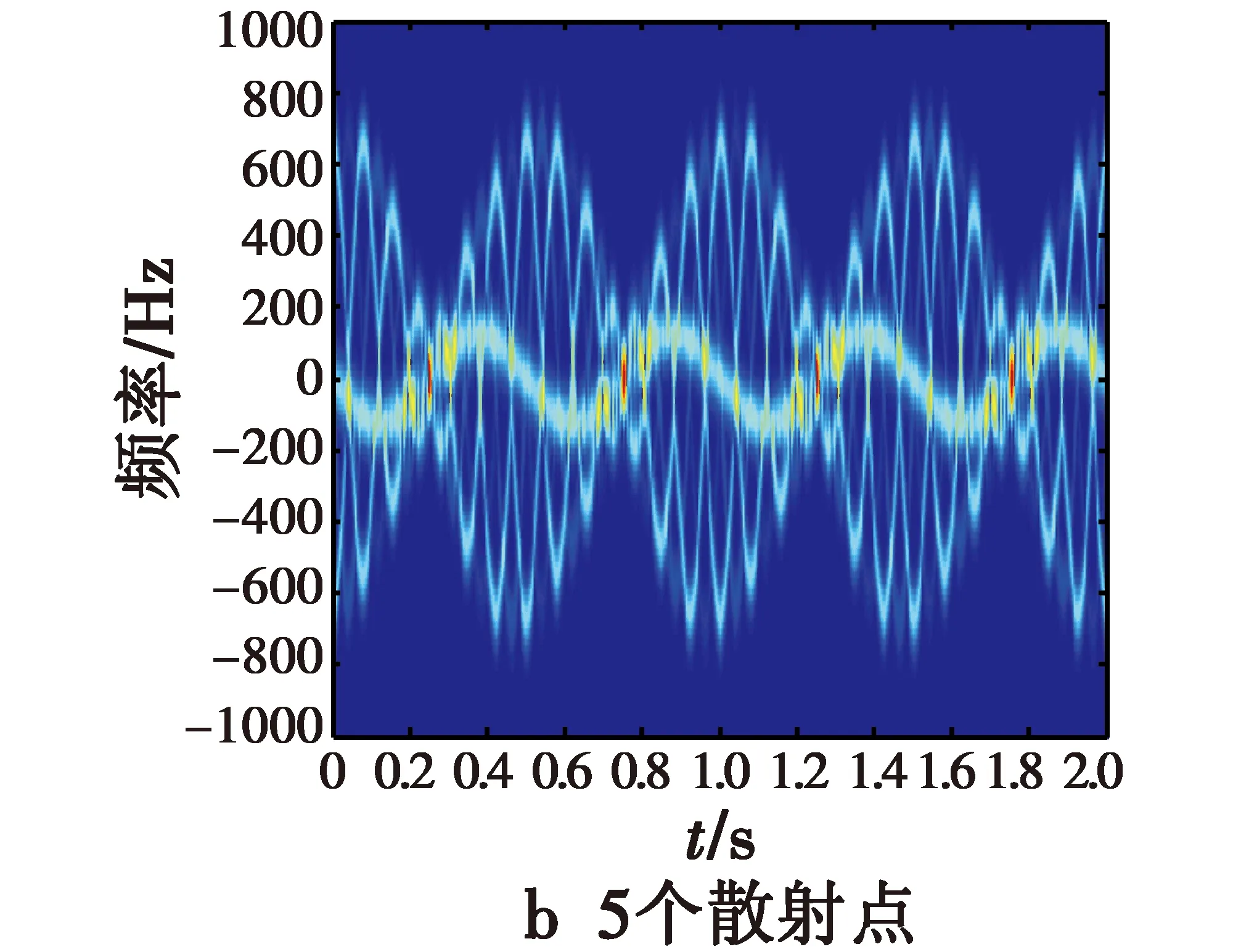
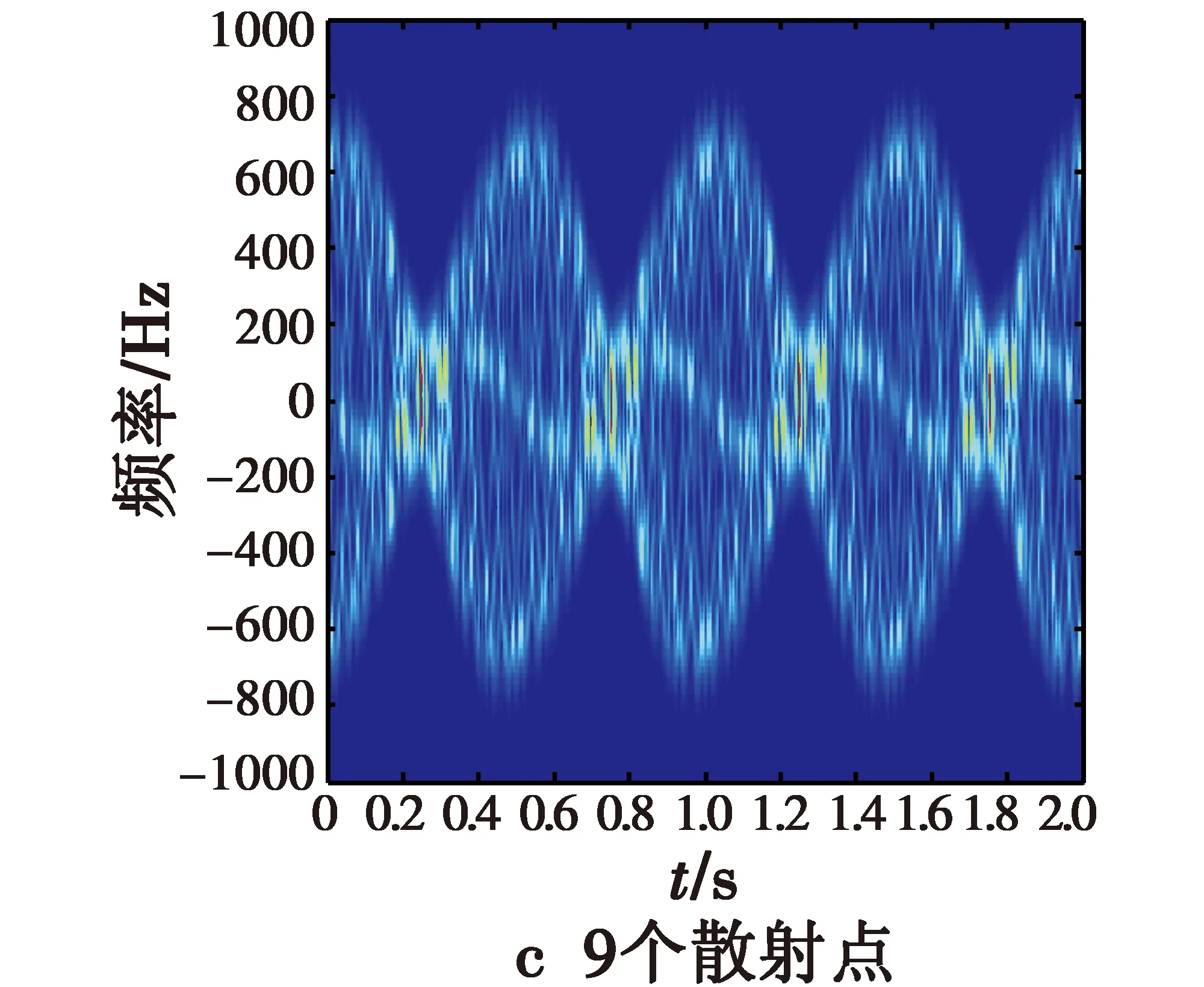
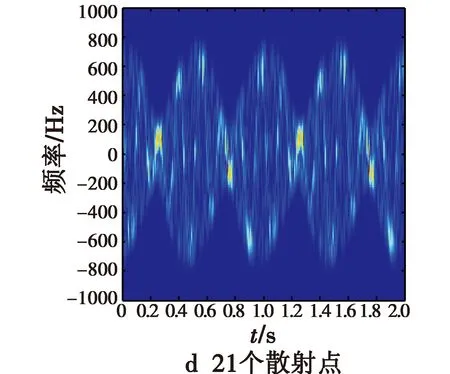
图4 第2类散射点的进动时频图Fig.4 Precession time-frequency of type Ⅱ for various scattering points

图4显示各种散射点的瞬时多普勒频率随时间的分布特性。由于这4种散射点分布的共同点都有1个散射点P0在自旋轴上，因此它对应的微动仅包含锥旋。其余的散射点都位于锥底，且不在自旋轴上，则其微动包括自旋和锥旋的共同运动。因此各种散射点分布情形都是2种微动合成的较复杂情况，其微多普勒频率随时间变化都为正弦曲线形式。随着散射点数的增加，微动合成的复杂程度增加，时频图模糊程度也增加，散射点引起的微多普勒频率随时间变化的交叉点数目迅速增加，而这些交叉点不是所有散射点瞬时频率的公共交点，此时这些交叉点的瞬时频率已不能用来表征多散射点情况下的微多普勒线性组合。如果对此结果做傅里叶变换则会在频谱图上出现毛刺，得到许多虚假的峰值点。

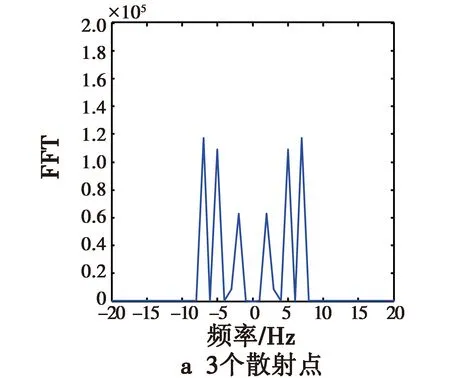
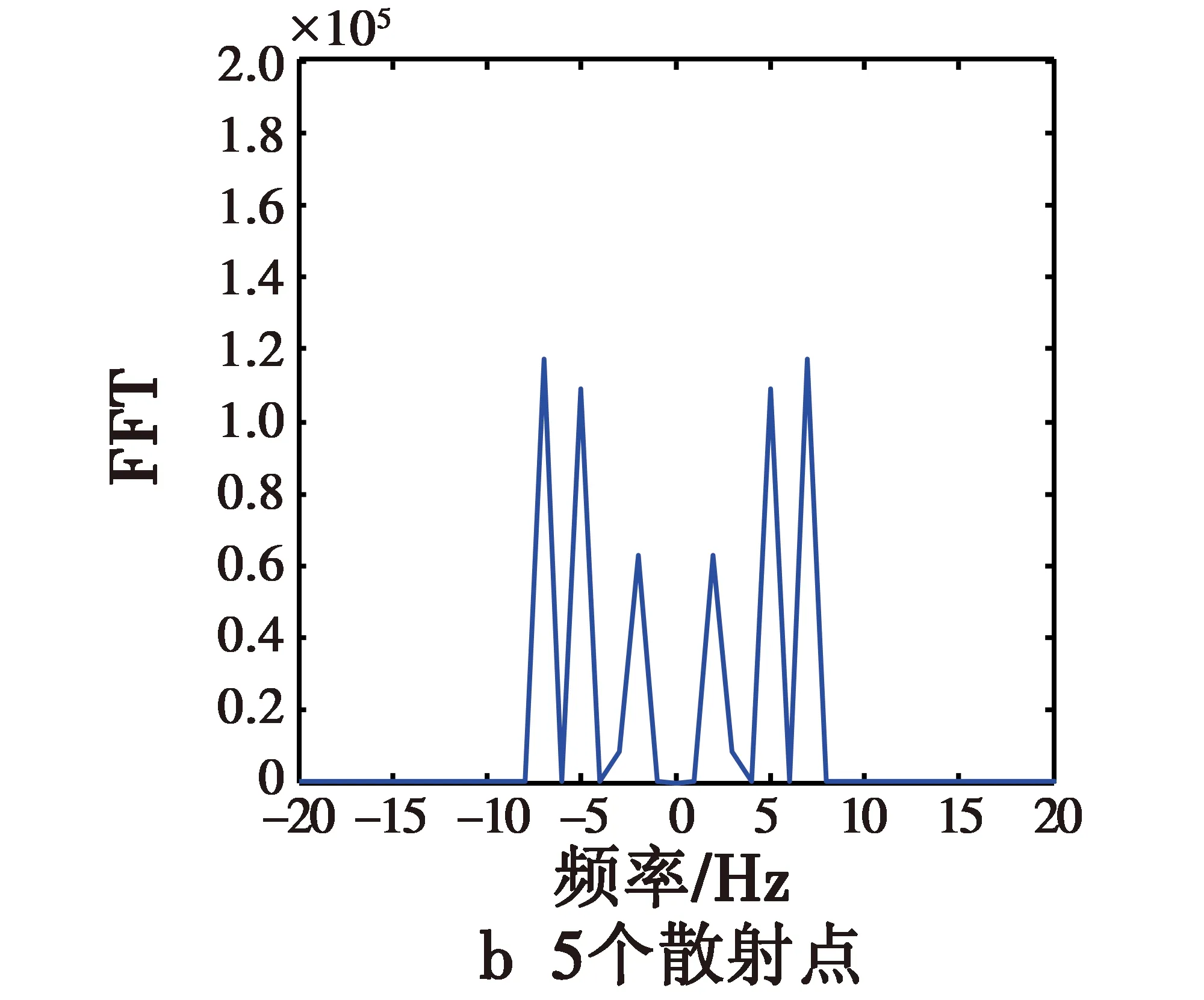
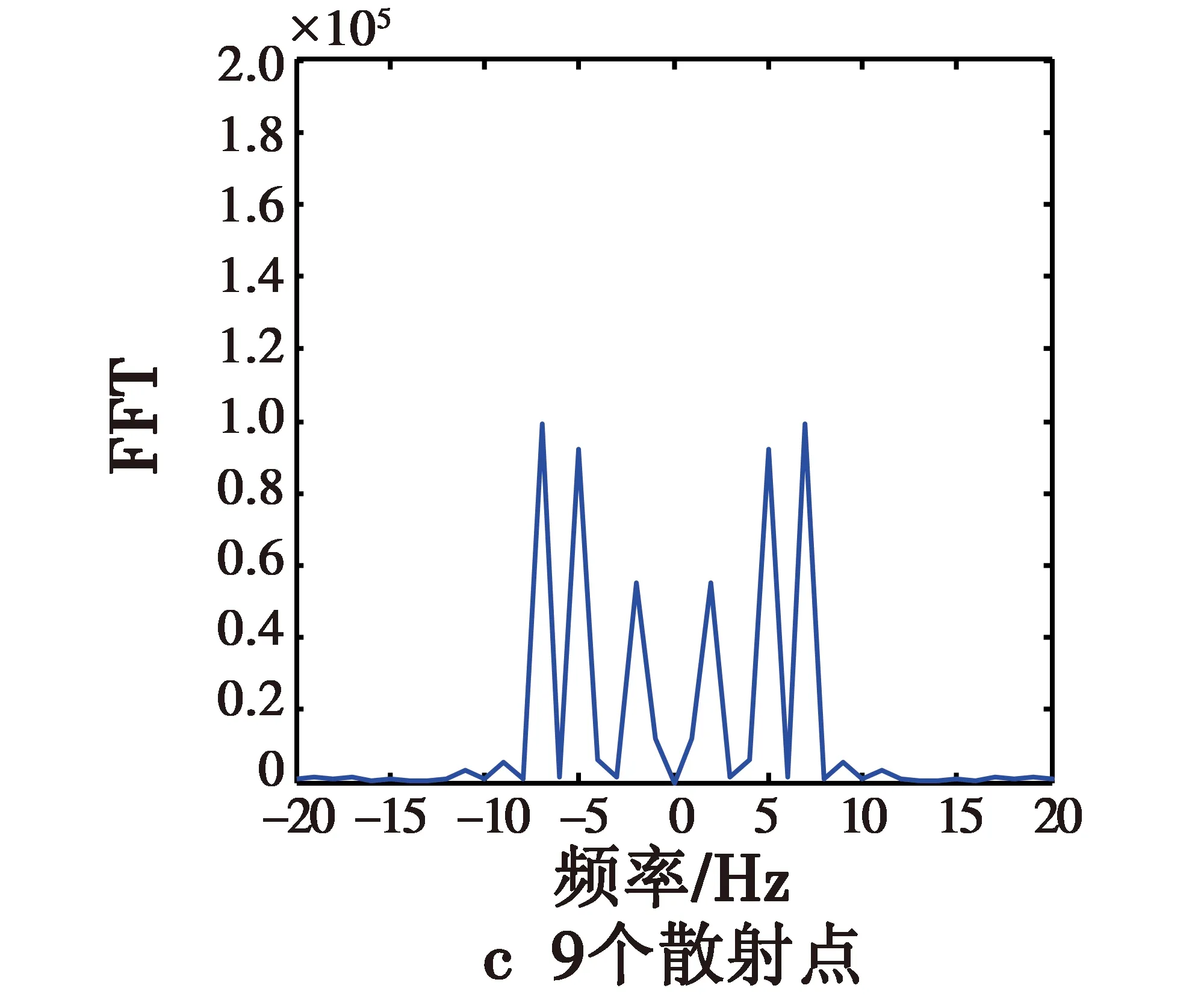
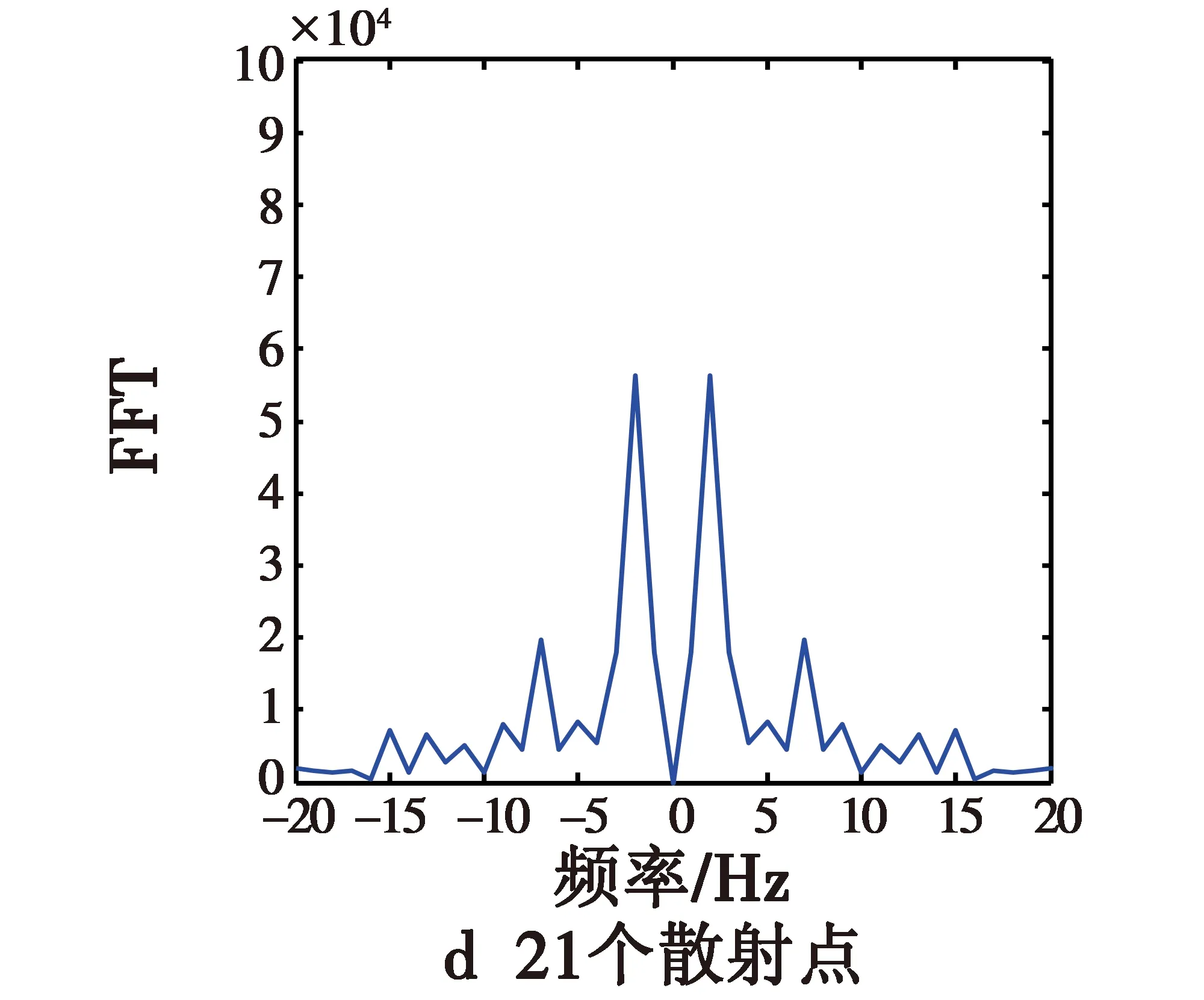
图5 第2类散射点的进动频谱图Fig.5 Precession spectrum of typeⅡ for various scattering points

图5为各种散射点的弹头目标的进动频谱图。可以看出，在横轴上存在6个强的频点值，从左向右分别对应-2 Hz,-5 Hz,-7 Hz,2 Hz,5 Hz,7 Hz，它们正好对应弹头微动的锥旋频率、自旋频率以及这二者的叠加频率，说明这样选择散射点可以较好地得到导弹微动的自旋和锥旋参数。当散射点数目较小，如3，5个散射点时，这6个峰值点明显，且没有其他的峰值点，这样就可以准确有效提取进动频率，即自旋和锥旋频率参数。但是，随着散射点个数的增加，频谱图上的毛刺开始逐渐增多，强度也相应增大，这使得在这6个频率峰值点外，其他频点上还存在一些峰值点，且随着散射点数的增加，这些附加的峰值的数目和强度也随之增加，如在散射点数为21时，从频谱图上可以看出，频率峰点除了2 Hz，5 Hz，7 Hz，-2 Hz，-5 Hz，-7 Hz这6个频点外，还有其他不期望的频率峰点9 Hz，12 Hz，-9 Hz，-12 Hz等。这些频率峰点将会影响对有效频率的提取。如果继续增加散射点个数，这些毛刺可能会淹没真实的频率值，导致目标的运动频率不能有效提取。总之，当散射点个数较少时，可以准确有效地提取自旋和锥旋频率参数；当散射点个数大于9时，其他频点开始逐渐增多，峰值逐渐增大，淹没真实频率信息的可能性增加，不利于有效频率参数的提取。

3.3 第3类散射点分布

此类实验分别选取5，7，18，23个散射点，其中,1个在弹头的锥形尖端，位置为P0=(0,0,1)，另外2个对称地位于弹头的锥形底部边沿，位置分别为P1=(0,-0.5,-0.5)，P2=(0,0.5,-0.5),其余的散射点随机分布在弹头的锥形面上。通过利用式(4)得到的信号进行时频分析，可仿真得到对应各种情形的时频分析结果。弹头的锥形面上随机分布2，4，15，20个散射点时的进动时频图如图6所示，通过傅里叶变换得到的对应进动频谱图如图7所示。

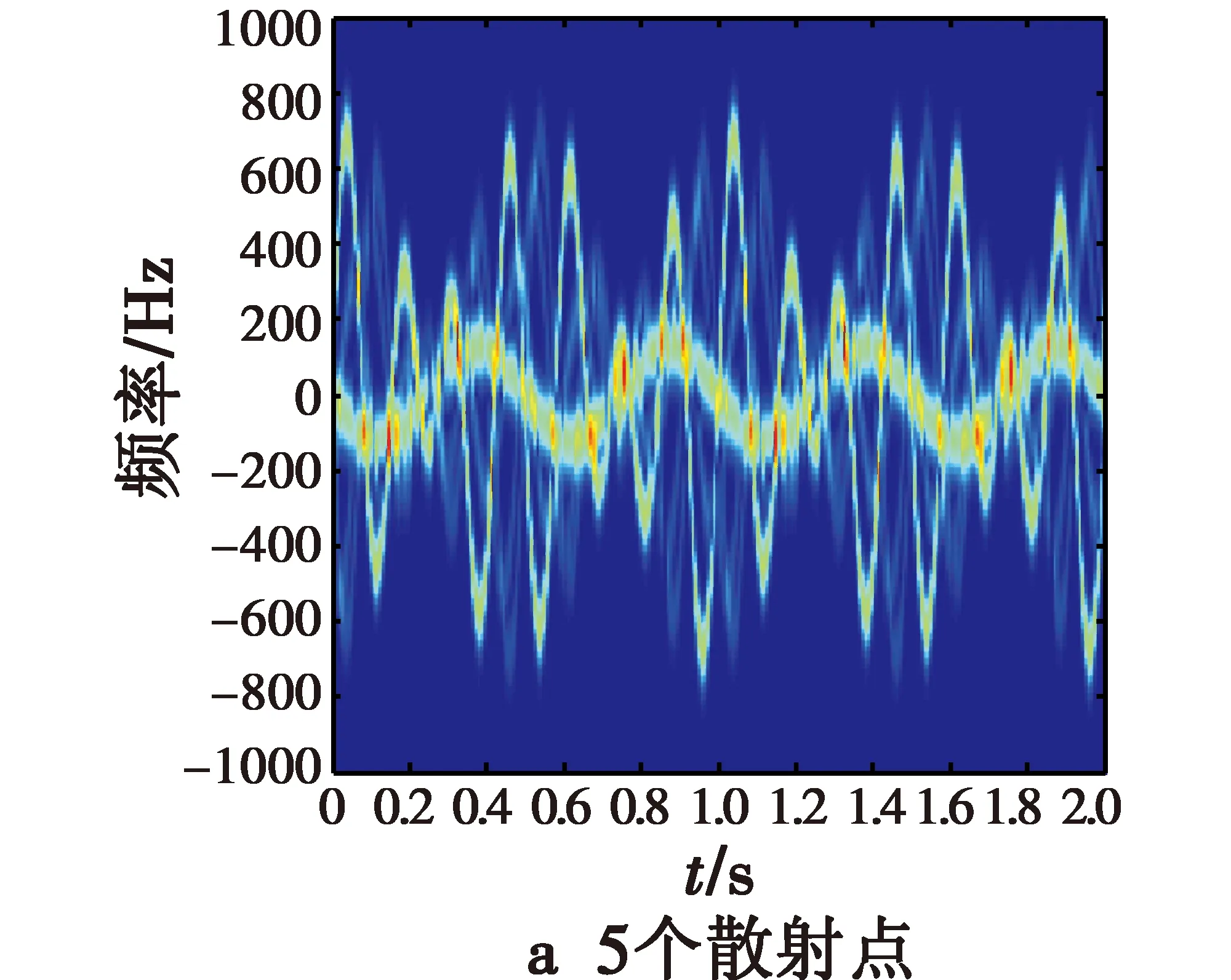
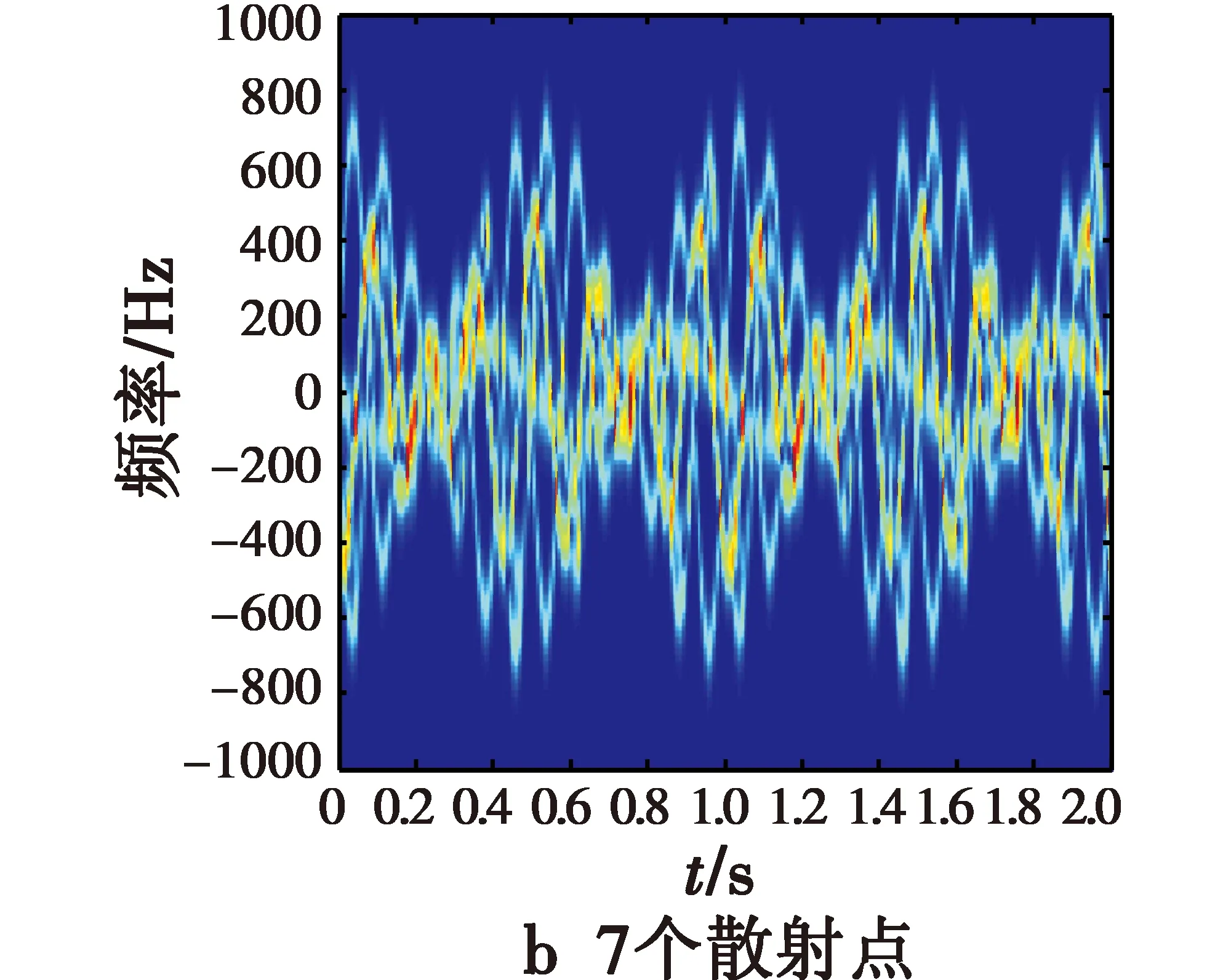
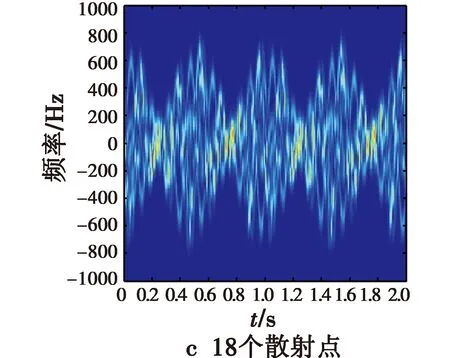
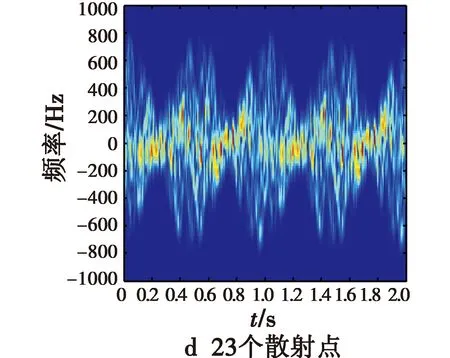
图6 第3类散射点的进动时频图Fig.6 Precession time-frequency of type Ⅲ for various scattering points

从图6可以看出，弹道导弹的尖端和底部两对称点的时频分布较为明显，而锥形面上随机分布散射点的时频分布不太明显。微动仍是包括自旋以及锥旋的共同运动，导弹整体对应的微多普勒频率随时间的变化曲线表现为较为复杂的形式，但是微动整体还存在周期性变化。随着随机分布散射点个数的增加，时频图变得更为复杂，模糊程度增加，交叉点的数目急剧增加，而且这些交叉点并不全是所有散射点的瞬时频率的公共交点，此时这些交叉点的瞬时频率已经不能用来表征多散射点情况下的微多普勒的线性组合。如果对此结果做傅里叶变换则会在频谱图上出现毛刺。

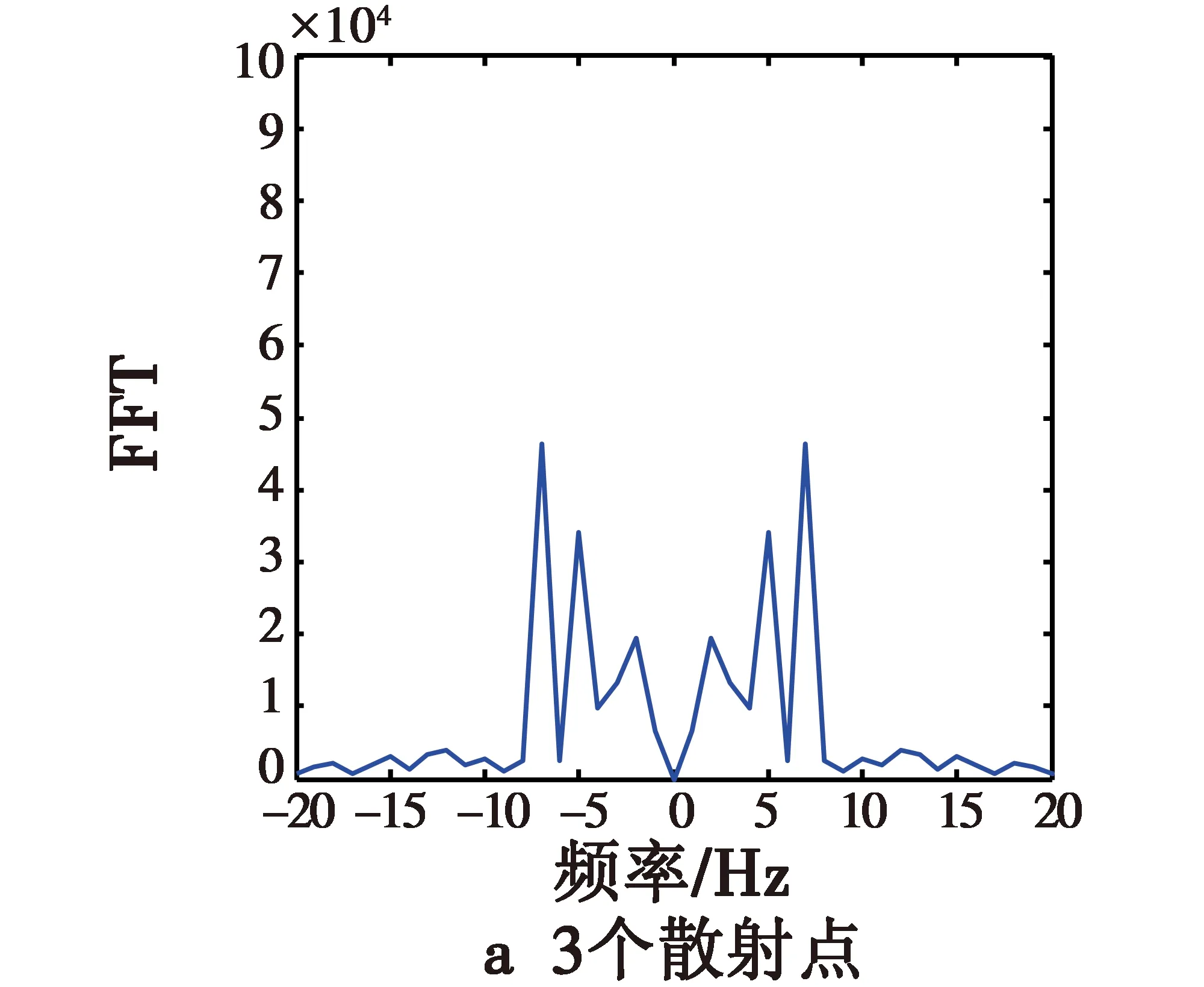
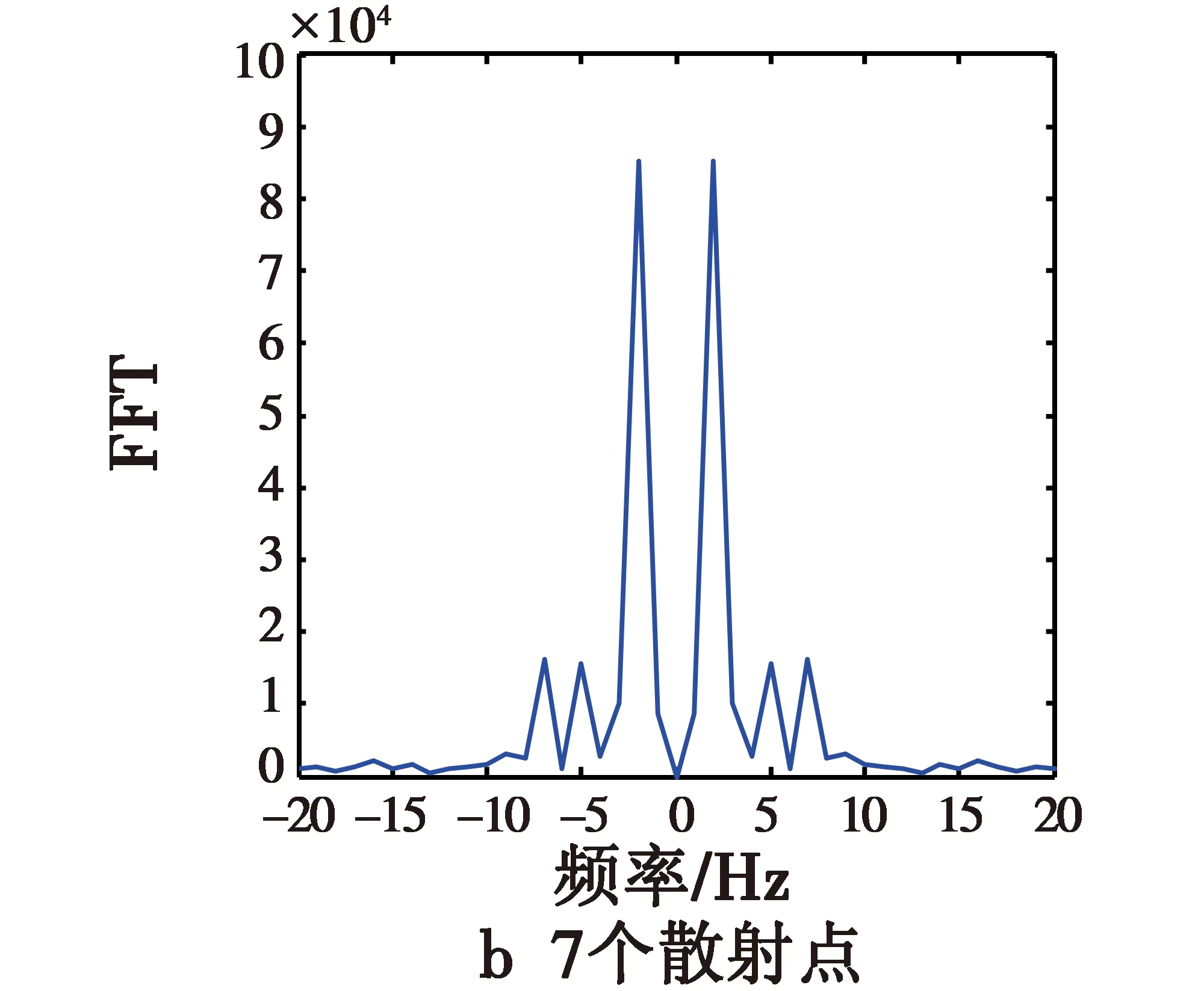
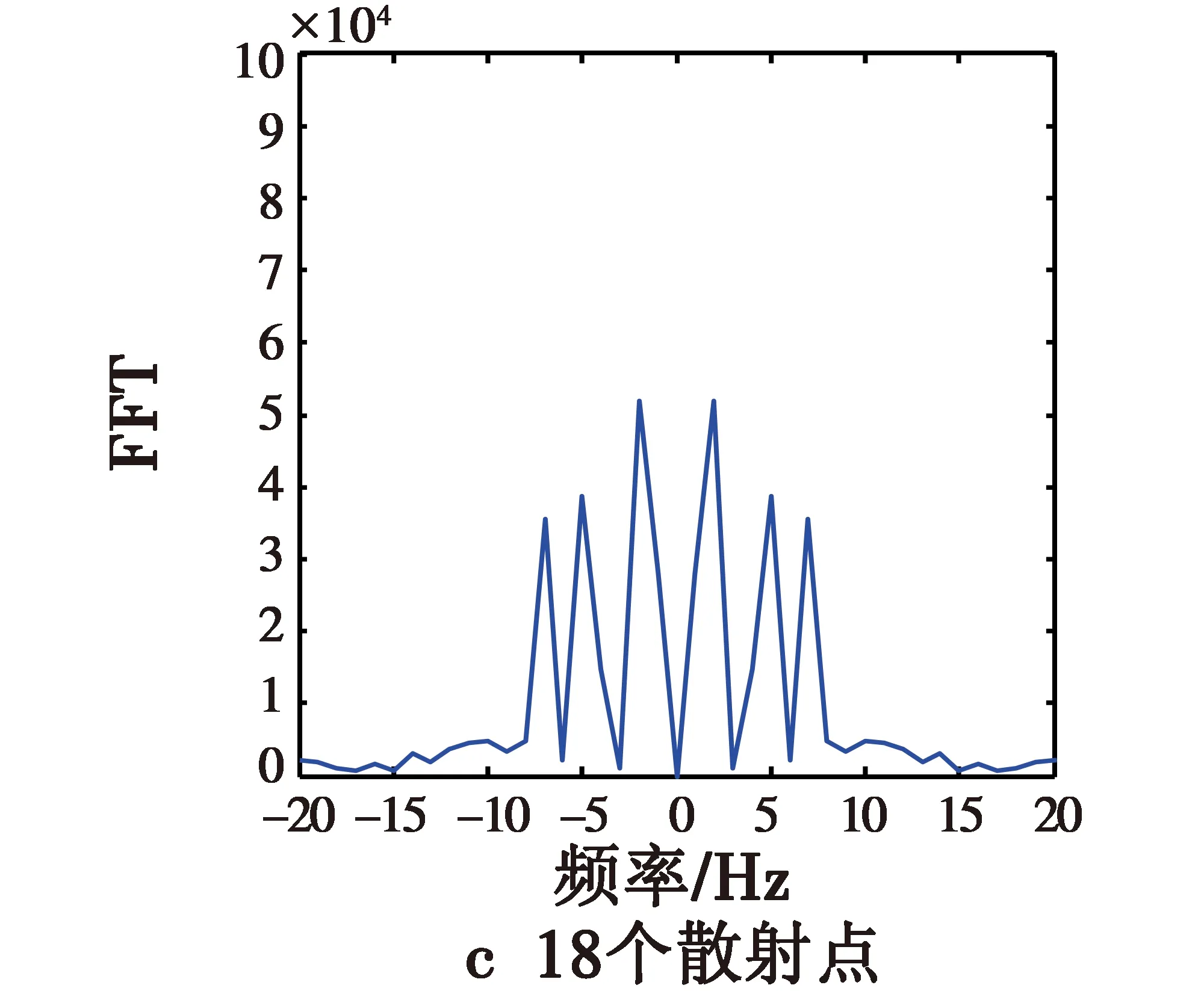
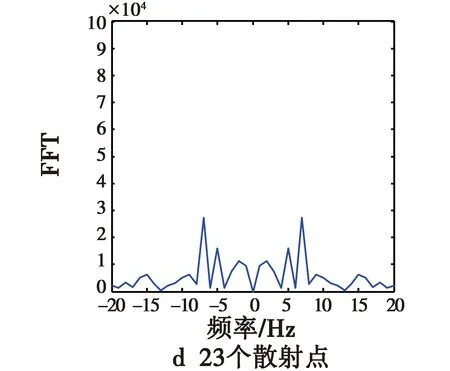
图7 第3类散射点的进动频谱图Fig.7 Precession spectrum of type Ⅲ for variousing scattering points

从频谱图8可以明显看出，频率轴上有6个强的频率值，即2 Hz,5 Hz,7 Hz,-2 Hz,-5 Hz,-7 Hz，这些频率是导弹的自旋频率5 Hz、锥旋频率2 Hz以及两者的叠加频率7 Hz,这表明采用该种散射点可以较好地得到导弹的进动参数，即自旋和锥旋频率参数。随着锥形表面上散射点个数的增加，如选择20个散射点，在频谱图中明显出现除导弹的自旋频率、锥旋频率及其两者组合频率之外的其他峰值较强的频率值，即9 Hz,15 Hz,-9 Hz,-15 Hz等，这种情况下导弹的真实运动频率会和虚假的峰值频点混在一起，不利于较好得到导弹的进动参数。如果随着锥形面上散射点的继续增加，真实频率的峰值最终将会完全淹没在虚假峰值中无法进行导弹进动参数的提取。

3.4 第4类散射点分布

设定30个散射点，这30个散射点全部在锥形表面随机选取。通过利用式(4)得到的信号进行时频分析，可仿真得到该情形的时频分析结果，如图8所示。

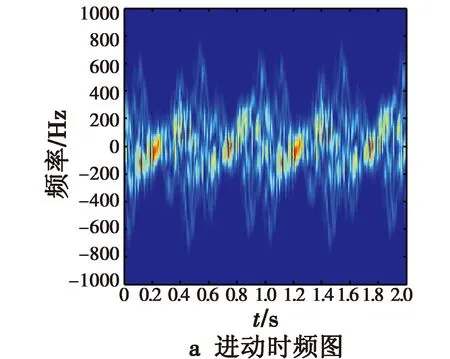
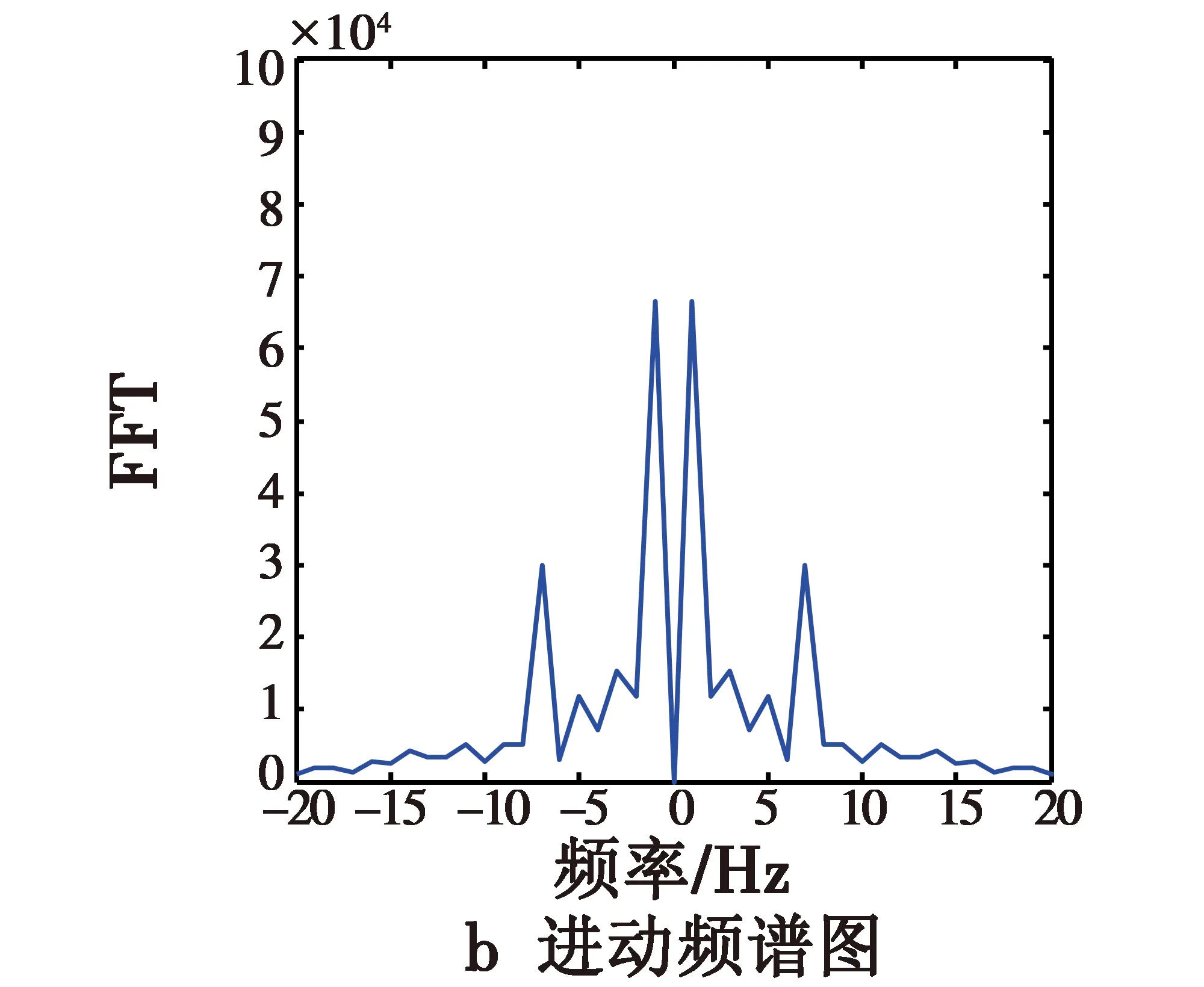
图8 30个散射点时的仿真结果Fig.8 Simulation results with 30 scattering points

从进动时频图8a可以看出，这种情况下时频图严重模糊，交叉点的数目急剧增加，且不全是所有散射点瞬时频率的公共交点，这些交叉点的瞬时频率已经不能用来表征多散射点情况下的微多普勒的线性组合。如对此结果做傅里叶变换则会在频谱图上出现很多毛刺。

从进动频谱图8b可以看出，频率轴上出现一些较强的频率值，即1 Hz,2 Hz,5 Hz,7 Hz,9 Hz,12 Hz,14 Hz,16 Hz,-1 Hz,-2 Hz,-5 Hz,-7 Hz,-9 Hz,-12 Hz,-14 Hz,-16 Hz等。此时导弹的真实运动频率会和虚假的峰值频点混在一起，并且有的虚假峰值已经超过了真实频点值，这样会造成虚假峰值点将会淹没真实的频点，从而影响导弹运动频率的有效提取。

4 结论

在利用时频分析法对弹道导弹的微动特征参数进行提取时，散射点的个数和位置对微动特征参数提取效果具有很大的影响。经过仿真与分析，得到如下结论。

1) 如果只在弹头顶上选用1个散射点，尽管能够很好地提取微动参数，但是只能提取到导弹进动的锥旋频率，而不能提取到其自旋频率。

2) 如果在弹头顶上选用1个散射点，其余散射点选在弹头的锥形底部边沿或随机在锥形底部，在散射点小于9个时可以较好地进行2个微动频率特征参数提取，当散射点大于9个时，则会因出现其他附加频率而增加提取微动特征参数的难度，甚至无法提取。

3) 如果在弹头顶上选用1个散射点，在弹头的锥形底部边沿对称选择2个散射点，其余在弹头锥形面上随机选择15个以下散射点则能够较好地进行导弹微动特征参数提取。随着散射点个数增加，则会因出现其他附加频率而增加提取微动特征参数的难度，甚至无法提取。

4) 如果只在锥形表面随机选取多个散射点，则不能有效地进行微动特征参数的提取。

总之，为了有效地提取微动特征参数，散射点应在弹头的顶上、锥形底部边沿、锥形面上都进行选择，但是总的散射点不能太多，最好不大于9个散射点。

[1] 陆伟宁.弹道导弹攻防对抗技术[M].北京:中国宇航出版社,2007.

[2] CHEN V C.雷达中的微多普勒效应[M].吴顺君，杜兰，刘宏伟,译.北京:电子工业出版社,2013.

[3] HU X W,TONG N N,HU G P,et al．Multi-ballistic targets resolution based on micro-Doppler[J].Systems Engineering and Electronics,2015,37(8):1734-1740.

[4] LI P,WANG D C,WANG L.Separation of micro-Doppler signals based on time frequency filter and Viterbi algorithm[J].Signal,Image and Video Processing,2013,7(3):593-605.

[5] 王璐.微动目标的运动参数估计和识别方法研究[D].西安:西安电子科技大学,2010.

[6] 王伟林,陈磊,雷勇军.弹道导弹中段诱饵微动特性研究[J].系统工程与电子技术,2016,38(3):487-492.

[7] 王义哲,冯存前,李靖卿,等.弹道中段多目标微多普勒分离方法[J].北京航空航天大学学报,2017,43(1):113-119.

[8] 罗迎,柏又青,张群,等.弹道目标平动补偿与微多普勒特征提取方法[J].电子与信息学报,2012,34(3):602-608.

[9] 鄢宏华,王文生.雷达目标微多普勒特征提取的频率稳定度约束[J].电波科学学报,2014,29(4):644-652.

[10] 喻荣梅,张仕元,肖健华.弹道目标移动散射点模型的微多普勒特征研究[J].测控技术,2014,33(3):154-156.

[11] CHEN V C,LING H.Time-frequency transforms for radar imaging and signal analysis[M].Boston:Artech House,2002.

Selection of Scattering Points for Obtaining Fretting Characteristics of Ballistic Missile

The use of radar to detect micro-Doppler frequency peculiar to the ballistic missile is a new method for target detection,and the selection of the scattering points on the target body is one of the key factors in the extraction of micro-Doppler characteristic parameters.Firstly,the motion model of the warhead of the ballistic missile is established and the extraction method for the micro-Doppler characteristic parameter of the warhead target based on the time-frequency analytical method is given.Then,the scattering points on the target body are classified into four types according to the different positions of them.By simulating the extraction of micro-Doppler characteristic parameters,the properties of the characteristic parameters changing with the scattering point are analyzed.The simulation results show that:1) The fretting characteristic parameters of the missile can be effectively extracted by selecting the scattering points from the top,the edge of the bottom and the conical surfaces of the missile cone,with the total number less than 9;and 2) With the increase of the number of the scattering points,the difficulty for extracting the fretting characteristic parameters is correspondingly increased,to the extent that it is impossible to extract the fretting characteristic parameters.

target identification; ballistic missile; micro-Doppler characteristics; characteristic parameter; scattering point

张瑜

张 瑜(1963-),男，河南沁阳人，1986年毕业于西安电子科技大学电磁场与微波技术专业，2005年前为中国电波传播研究所高级工程师，现为河南师范大学物理与信息工程学院教授。曾先后主持国家“八六三”、自然科学基金、国防预研项目7项，省部级研究项目10项，参与研究项目数十项，在不同的学术刊物上发表论文100多篇，多次获部、省、市科技成果奖。目前主要从事电磁波与微波技术理论与应用研究工作。

利用雷达探测弹道导弹特有的微多普勒特征是进行目标识别的新方法，而目标体上散射点的选取是影响微多普勒特征参数提取的关键因素之一。首先建立弹道导弹弹头运动模型并简要给出基于时频分析法的弹头目标的微多普勒特征参数提取方法，然后根据散射点位置不同将目标体上散射点分4类，而后通过仿真微多普勒特征参数的提取，进而研究特征参数随散射点的变化特性。仿真结果表明：在导弹锥形的顶部、底部边沿、锥形面上选择总量小于9的散射点，可以有效地提取导弹的微动特征参数。随着散射点数量的增加，提取微动特征参数的难度也相应增加，甚至无法提取微动特征参数。

TN95

10.3969/j.issn.1671-637X.2017.11.001

张瑜，赵小纳，王召迎.弹道导弹微动特征散射点的选取[J].电光与控制，2017，24( 11) : 1-6.ZHANG Y，ZHAO X N，WANG Z Y.Selection of scattering points for obtaining fretting characteristics of ballistic missile[J].Electronics Optics & Control，2017，24( 11) : 1-6．

国家自然科学基金(61077037);河南省重点科技攻关计划(172102210046)