网格形声纳浮标阵及其搜索效能评估

丛红日，褚 政，粘松雷

(海军航空工程学院指挥系，山东 烟台 264001)

网格形声纳浮标阵及其搜索效能评估

丛红日，褚 政，粘松雷

(海军航空工程学院指挥系，山东 烟台 264001)

结合声纳浮标的性能特点和检查性搜潜的需求，研究提出了基于元网格的网格形声纳浮标阵搜潜方法。构造了元网格，通过建立模型，研究了元网格的大小和所需声纳浮标的数量，进而研究了网格矩阵形式的网格形声纳浮标阵的元网格数量、声纳浮标数量和搜索面积。对网格形声纳浮标阵的搜索效能进行了仿真评估，并通过对仿真结果的分析得出了能用于指导作战使用的结论。

航空反潜； 声纳浮标； 网格形声纳浮标阵； 元网格； 搜索效能评估

0 引言

对潜搜索是反潜作战的主要阶段，很大程度上决定着反潜作战的成败。在反潜作战中，经常需要对某一特定海域展开搜索，以查明该海域有无敌潜艇活动，为我方兵力使用该海域消除威胁创造条件，典型的如在我预定演习海域或航母编队综合作战区的反潜清扫等。这属于典型的面积型搜索(区域搜索)，通常采用检查性搜索方法[1]。

上述作战任务经常需要使用反潜机(反潜直升机或反潜巡逻机)来完成，或使用反潜机与反潜水面舰艇等其他反潜兵力协同完成。使用反潜机开展检查性搜索时，根据任务特点和航空搜潜装备的性能特点，使用声纳浮标进行搜索是比较理想的选择[2]。

使用声纳浮标搜潜时，通常需要由多枚声纳浮标组成声纳浮标阵来执行搜索任务。声纳浮标阵的阵型是影响声纳浮标阵搜潜效能的重要因素[3]。

声纳浮标阵的阵型有很多，如直线阵、弧线阵、方形阵、圆形阵、十字阵、星形阵等，其中，适用于检查性反潜的浮标阵阵型主要有方形阵、圆形阵、十字阵、星形阵、“X”形阵、“回”形阵、“田”形阵、三角形阵等，这些阵型均能取得比较好的搜索效能[4]，但问题是，这些阵型类型很多，在实际作战时选用比较困难，而且有些阵型虽然搜索效能较高，但布设起来比较复杂。那么，有没有一种既便于布设同时搜索效能又较高的规范性声纳浮标阵阵型呢？

本文提出基于网格矩阵的声纳浮标阵搜索方法，并采用仿真方法对其搜索效能进行评估，为检查性反潜时使用声纳浮标搜潜的作战使用提供了指导。

1 基于网格矩阵的声纳浮标搜索方法

1.1 网格形声纳浮标阵的涵义

网格的概念起源于信息技术中的信息栅格，在军事领域已得到广泛应用。基于网格矩阵的声纳浮标搜索方法，就是把整个搜索区域布设成由若干元网格连接而成的网格形声纳浮标阵，通过构建网格矩阵来进行大面积搜索，如图1所示。元网格是网格形声纳浮标阵的基本组成单元，元网格的组合，就构成了网格矩阵。

图1 网格形浮标阵示意图Fig.1 Grid sonobuoy array

1.2 元网格

网格形声纳浮标阵中的元网格，就是组成该声纳浮标阵的最基本的网格单元。该网格单元体现为一个正方形的声纳浮标阵，该正方形声纳浮标阵的每一条边，均由相同数量的若干枚声纳浮标(通常为被动全向声纳浮标)组成，相邻2枚声纳浮标之间的间距也均相等,如图2所示。

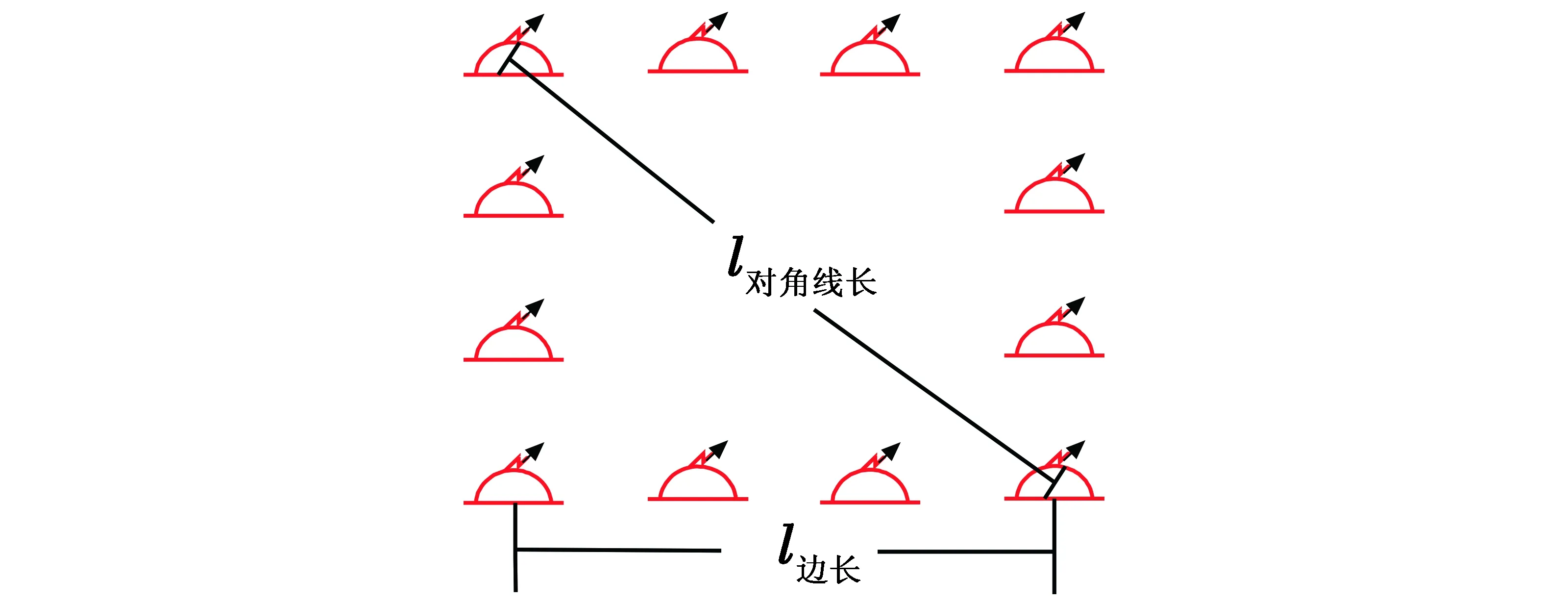
图2 子网格浮标阵示意图Fig.2 Sub-grid sonobuoy array

之所以把元网格规定为正方形声纳浮标阵，主要有以下两方面的原因：首先，研究表明，在一般情况下，方形声纳浮标阵的搜索效能较高[5]；其次，检查性搜索时，通常无法判断敌潜艇的位置和航向，可认为敌潜艇的位置和航向呈均匀分布[6]。因此，布设成正方形声纳浮标阵，就可以保证只要敌潜艇在该正方形声纳浮标阵(即元网格)的范围之内，无论其航向如何，均能取得较高的搜索效能。

1.2.1 元网格的大小

元网格的大小可用其边长l边长或对角线长l对角线长表示。设监听声纳浮标的时间为t监听，敌潜艇的航速为v敌潜，声纳浮标有效探测距离为D，为了取得理想的搜索效能，应使

l对角线长-2D≤v敌潜×t监听。

(1)

另一方面，在保证较高搜索效能的前提下，为了在声纳浮标消耗量一定的情况下尽可能地提高该正方形声纳浮标阵(元网格)的搜索范围，一般应使

l对角线长=v敌潜×t监听+2D。

(2)

根据几何学知识，显然

(3)

因此

(4)

1.2.2 元网格每边的声纳浮标数量

元网格的边长一旦确定，则可以根据相邻声纳浮标之间的间距来确定该元网格每边的声纳浮标数量[7]。设相邻声纳浮标之间的间距为d，元网格任意一条边上布设声纳浮标的数量为n(n为不小于2的自然数)，则

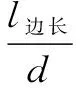
(5)

式中,算子“「⎤”表示向上取整运算。

1.2.3 元网格声纳浮标的总数量

设布设元网格所需声纳浮标的总数量为n元网格，则显然

n元网格=4(n-1)=4n-4 。

(6)

1.3 网格形声纳浮标阵元网格的数量及所需声纳浮标的数量

1.3.1 元网格的数量

设组成整个网格形声纳浮标阵的元网格的数量为m总，其中一条边上元网格的数量为m1，在与之垂直的另外一条边上元网格的数量为m2，则显然

m总=m1m2。

(7)

每一条边上元网格的数量取决于搜索区的大小和元网格的大小。检查性反潜时，上级分配给航空反潜兵力的搜索区通常为方形(长方形或正方形)[8]，即使搜索区不是方形(如圆形或椭圆形)，也可以通过一定方法确定出等价的方形。因此，以搜索区是方形为例进行讨论。设方形搜索区的两个边长分别为L1和L2，网格形声纳浮标阵以搜索区两条边为基准进行布设，则该搜索区两条边上元网格的数量为

(8)

式中,算子“[]”表示取整运算。

1.3.2 所需声纳浮标的数量

设布设由多个元网格连接而成的整个网格形声纳浮标阵所需要的声纳浮标的总数量为n总，则

n总=m1[m2n子网格-(m2-1)n]-(m1-1)[m2n-

(m2-1)]=m1[m2(4n-4)-(m2-1)n]-

(m1-1)[m2n-(m2-1)]=2m1m2n-

3m1m2+m1n+m2n-m1-m2+1 。

(9)

对典型元网格和不同网格矩阵构成时整个网格形声纳浮标阵所需要的声纳浮标数量的计算结果见表1。

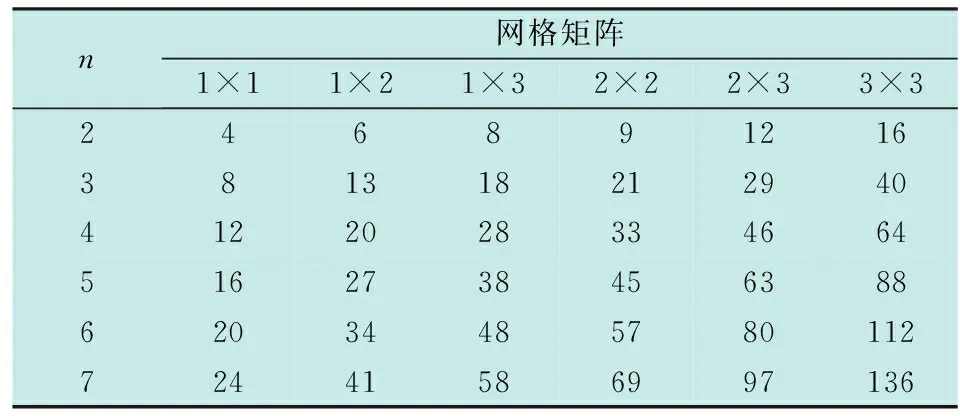
表1 网格形声纳浮标阵声纳浮标数量计算结果

需要说明的是，由于反潜机所携载声纳浮标总数的限制[9]，在实际布设声纳浮标阵时，声纳浮标的数量不可能太多，表1所示的计算结果中，声纳浮标数量较多的情况在实际布设声纳浮标阵时可能会受到局限，仅供参考。

1.4 网格形声纳浮标阵的搜索面积

假设布设声纳浮标阵时相邻两个浮标之间的间距均为声纳浮标有效作用距离的2倍，即d=2D，设整个声纳浮标阵的搜索面积为S,则通过对网格形声纳浮标阵的分析可知

S=2D(m1n-m1+1)2D(m1n-m1+1)=

4D2(m1m2n2-2m1m2n+m1n+m2n+m1m2-

m1-m2+1) 。

(10)

通过对式(9)和式(10)的综合分析可知，在声纳浮标消耗量相等的情况下，n越大，则S越大。例如，假设声纳浮标有效作用距离为2 km，即D=2 km，则从表1中选取典型情况进行对比，如表2所示。

表2 声纳浮标消耗量相等(或相近)情况下不同声纳浮标阵搜索面积对比

1.5 网格形声纳浮标阵的优势

与一般用于检查性搜索的声纳浮标阵相比，网格形声纳浮标阵具有以下优势。

1) 规范性强。整个网格形声纳浮标阵由相互连接在一起的若干个元网格组成，构成网格矩阵，具有很强的规范性。主要表现在以下几个方面：

① 元网格为正方形声纳浮标阵，布设和监听都比较容易；

② 整个浮标阵由完全相同的若干元网格组成，符合信息栅格的思想理念，能够广泛应用于对较大面积海区的搜索；

③ 能够方便地确定所需要声纳浮标的数量以及声纳浮标阵的搜索面积；

④ 能够方便地根据实际情况对搜索效能进行控制，并能取得较高的搜索效能。

2) 灵活性。布设网格形声纳浮标阵，适用于不同大小的作战海区、不同装备性能及不同水文条件下搜潜。首先，正方形元网格的大小(边长、对角线长)、每条边上声纳浮标的数量以及相邻声纳浮标之间的间距都可根据声纳浮标的性能(探测距离)、战场环境条件(主要影响声纳浮标有效探测距离)、对敌潜艇情况的掌握(可能的航速)、最大监听时间等来灵活进行调整，适应不同的作战需要，例如，通过选取不同声纳浮标数量或适当扩大或缩小声纳浮标间隔就能组成不同的元网格；其次，可根据所指定搜索任务区的大小以及可用声纳浮标的数量等因素来合理确定整个声纳浮标阵的元网格的数量，确定出合理的网格矩阵，适应不同大小海域的搜索。

3) 便于开展效能评估。孙子兵法有云，算则胜。效能评估是科学指挥的前提。网格形声纳浮标阵由若干个元网格组成，每个元网格情况相同，根据检查性搜索的特点，敌潜艇在每个元网格中的分布也是相同的，因此，整个网格形声纳浮标阵搜索效能的评估就可以简化成对单个元网格搜索效能的评估，而元网格是规范的正方形声纳浮标阵，其搜索效能评估相对简便[10]，从而可以方便地开展搜索效能评估。

2 网格形声纳浮标阵搜索效能评估

只需要对元网格的搜索效能评估即可。

2.1 想定条件

1) 上级指定的检查性搜索区域为一边长为30 n mile(1 n mile=1852 m)的正方形区域，搜索时使用被动全向声纳浮标布设网格形声纳浮标阵进行搜索。在此区域内，敌潜艇的初始位置和航向均服从均匀分布，且敌潜艇在搜索过程中不改变航向[11]。

2) 声纳浮标有效探测距离为2 km，即D=2 km，声纳浮标最大监听时间为3 h，即t监听=3 h。

3) 敌潜艇为常规动力潜艇，其航速分别设定为4 kn,6 kn(1 kn=1852 m/h)。

2.2 参数计算

2.2.1 元网格边长

使用式(4)通过计算确定出敌潜艇不同航速时在想定条件下的元网格边长l边长，计算结果见表3。

表3 敌潜艇不同航速时元网格的边长

2.2.2 元网格每条边的声纳浮标数量

元网格每条边的声纳浮标数量n取决于元网格的边长l边长和相邻声纳浮标之间的间距d。为了保证比较理想的搜索效能，通常情况下，相邻声纳浮标之间的间距应小于等于声纳浮标有效探测距离的2倍。在此前提下，再基于表3的计算结果，用式(5)就能够计算出敌潜艇不同航速时元网格每条边上声纳浮标的数量n，计算结果为：当敌潜艇航速v敌潜为4 kn时，n=5；当敌潜艇航速v敌潜为6 kn时，n=7。

但由于声纳浮标的数量有限，为了节省声纳浮标，可适当加大声纳浮标的间距，从而减少元网格每条边的声纳浮标数量，当然，在这种情况下，声纳浮标阵的搜索效能必然会降低。综合考虑，结合效能仿真评估的需要，当v敌潜为4 kn时，n的取值确定为3，4，5；当v敌潜为6 kn时，n的取值确定为5,6,7。

2.2.3 网格形声纳浮标阵的网格数量

使用式(7)和式(8)，就可以通过计算确定出敌潜艇不同航速时整个网格形声纳浮标阵每条边的网格数量m1,m2和网格的总数量m总，计算结果见表4。

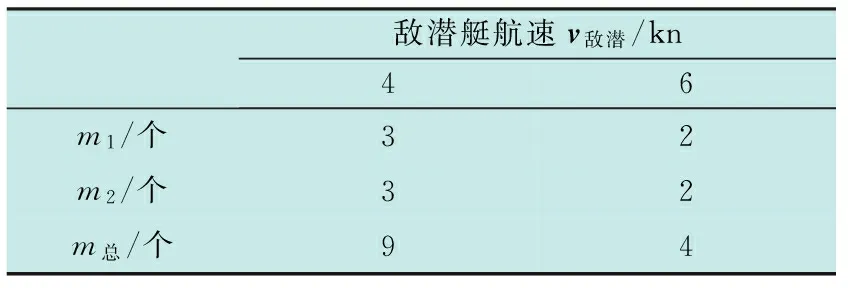
表4 敌潜艇不同航速时声纳浮标阵的网格数量

即：当敌潜艇航速为4 kn时，需要布设3×3的网格矩阵;当敌潜艇航速为6 kn时，需要布设2×2的网格矩阵。

2.2.4 网格形声纳浮标阵所需声纳浮标的总数量

使用式(9)确定出敌潜艇不同航速时网格形声纳浮标阵所需声纳浮标的总数量n总，计算结果见表5。

表5 敌潜艇不同航速时网格形声纳浮标阵所需声纳浮标的总数量

2.3 仿真结果

检查性反潜时方形声纳浮标阵搜索效能评估已经比较成熟。借鉴文献[11-13]中的搜索效能评估方法，采用蒙特卡罗法对元网格的搜索效能进行评估。

敌潜艇航速为4 kn时，元网格每边分别布设3枚、4枚、5枚声纳浮标时的搜索效能仿真计算结果见图3。

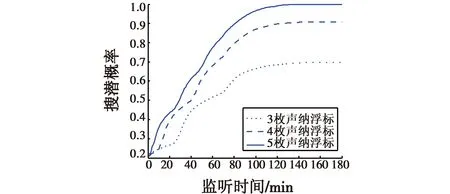
图3 敌潜艇航速4 kn时网格形声纳浮标阵搜索效能仿真结果Fig.3 Probability of grid sonobuoy array searching when enemy submarine speed is 4 kn

敌潜艇航速为6 kn时，元网格每边分别布设5枚、6枚、7枚声纳浮标时的搜索效能仿真计算结果见图4。

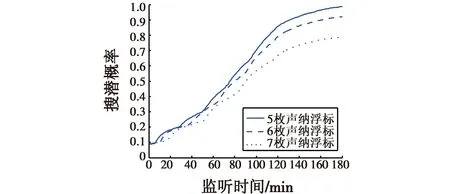
图4 敌潜艇航速6 kn时网格形声纳浮标阵搜索效能仿真结果Fig.4 Probability of grid sonobuoy array searching when enemy submarine speed is 6 kn

2.4 仿真结果分析

通过对仿真结果进行分析，可以得出如下结论。

1) 搜索概率随着监听时间的增加而提高。监听时间对声纳浮标阵的搜索效能有重要影响[14]。由图3、图4可以看出，网格形声纳浮标阵搜潜概率随监听时间增加不断提高，延长声纳浮标的监听时间，是提高声纳浮标阵搜潜概率的重要手段；但搜潜概率与监听时间的变化并不是简单的线性关系，前期搜潜概率随监听时间变化较为明显,中期变化较为缓和,后期搜潜概率趋于稳定。例如在图3中，以元网格每边声纳浮标数量4枚为例，监听时间为140 min时，搜潜概率为0.887；当监听时间为180 min时，搜潜概率为0.888,这说明后期虽然增加了对声纳浮标的监听时间，但是获得的搜潜概率提升并不明显；在实际作战使用时，通常需要综合考虑声纳浮标的有效工作时间、反潜机的留空时间、反潜任务时效等因素，合理确定监听时间。

2) 敌潜艇航速对搜索概率影响较大。当敌潜艇航速不同时，通常需要布设单边数量不同的元网格浮标阵对敌潜艇进行搜索。对比图3、图4可知，敌潜艇航速越低，对使用声纳浮标阵进行搜索越不利，结合表4的结果，当保证取得较高的搜索效能时，所需要使用的声纳浮标的数量就越多。在实际作战使用时，应根据对敌潜艇可能航速的判断和可用声纳浮标的数量，通过计算科学确定元网格，并进而布设整个网格形声纳浮标阵进行搜索。

3 结束语

结合声纳浮标的性能特点和检查性搜潜的需求，提出了基于元网格的网格形声纳浮标阵搜潜方法。构造了元网格，通过建立模型，研究了元网格的大小和所需声纳浮标的数量，进而研究了网格矩阵形式的网格形声纳浮标阵的元网格数量、声纳浮标数量和搜索面积。对网格形声纳浮标阵的搜索效能进行了仿真评估，并通过对仿真结果的分析得出了能用于指导作战使用的结论。

网格形声纳浮标阵既有规范性强、方便作战使用和效能评估的优势，又具有很强的灵活性和适应性，能够根据搜索区域大小和敌潜艇情况进行灵活调整，适用于各种不同情况下的检查性搜索，能够为使用声纳浮标进行检查性搜潜提供指导，也能为相关研究提供借鉴。

[1] 陶晨辰，鞠建波，王承祥,等．区域性检查搜潜中声纳浮标的使用方法[J]．火力与指挥控制，2013，38(10)：94-96.

[2] 匡贡献，谢志敏．声纳浮标阵目标搜索优化布放算法[J]．海军航空工程学院学报，2011，26(5)：508-512.

[3] 丛红日，沈培志，栾玉佳．检查性反潜时声纳浮标阵阵型优化[J]．海军航空工程学院学报，2014，29(4)：391-396.

[4] 杨日杰，王正红，周旭，等．浮标阵形对搜潜效能影响的研究[J]．计算机仿真，2009，26(12)：16-20.

[5] 曾海燕，杨日杰，周旭．声纳浮标搜潜优化布放技术研究[J]．指挥控制与仿真，2012，34(1)：82-85.

[6] 赵志允，孙明太，韩强．潜艇运动对被动声纳浮标搜索的影响[J]．指挥控制与仿真，2013，35(5)：51-54.

[7] 杨日杰，周旭，曾海燕．被动全向声纳浮标跟踪潜艇的优化布放方法[J]．指挥控制与仿真,2011，33(5)：80-83.

[8] 戚学文，严建钢，金复鑫,等．直升机声纳浮标包围阵搜潜模型研讨[J]．电光与控制，2013，20(12)：10-13.

[9] 丛红日，周海亮，于吉红．基于网络化航空搜潜体系的声纳浮标检查性搜索方法[J]．海军航空工程学院学报，2016，31(2)：195-200.

[10] 许爱强，盛沛，谭勖．机载浮标搜潜系统搜潜效能评估模型[J]．兵工自动化，2011，30(8)：43-45.

[11] 丛红日．声纳浮标阵搜潜效能通用仿真模型研究[J]．系统仿真技术，2010，6(2)：104-109.

[12] 蒋志忠，杨日杰，李大龙,等．反潜巡逻机布放包围浮标阵应召搜潜建模与仿真[J]．海军航空工程学院学报，2011，26(4)：422-426,436.

[13] 罗木生，侯学隆，郑保华．网络中心与平台中心的声纳浮标探测概率建模[J]．火力与指挥控制，2013，38(4)：154-157.

[14] 袁杰,丛红日,李琰,等．监听时间对声纳浮标阵检查性搜索效能影响仿真[J]．海军航空工程学院学报，2010，25(6)：711-715.

GridSonobuoyArrayandItsSearchingEfficiencyEvaluation

CONG Hong-ri, CHU Zheng, NIAN Song-lei

(Department of Command,Naval Aeronautical Engineering Institute,Yantai 264001,China )

Considering the characteristics of the sonobuoy and the demand for the checking search,we put forward a method for searching grid sonobuoy arrays based on the meta-grid.First,the meta-grid is constructed.Then the size of the meta-grid and the needed number of sonobuoys are studied in detail by building models.And then the number of the meta-grid,the number of sonobuoys and the searching area of the grid sonobuoy array are analyzed.In the end,the searching efficiency of the grid sonobuoy array is evaluated by simulation,and an analysis is made to the simulation results and conclusions useful for military operations are obtained.

aerial anti-submarine; sonobuoy; grid sonobuoy array; meta-grid; searching efficiency evaluation

丛红日，褚政，粘松雷.网格形声纳浮标阵及其搜索效能评估[J].电光与控制，2017，24( 11) : 38-42.CONG H R，CHU Z，NIAN S L．Grid sonobuoy array and its searching efficiency evaluation[J].Electronics Optics & Control，2017，24( 11) : 38-42．

2016-12-29

2017-01-18

全军军事类研究生重点资助课题(2015JY395)

丛红日(1966 —),男，山东威海人，博士，副教授,研究方向为航空反潜战术和装备管理。

TN925.4

A

10.3969/j.issn.1671-637X.2017.11.008