多维地震作用下高柔结构的地震响应*

魏文晖 黄玮松 薛广文 张迪

(武汉理工大学 道路桥梁与结构工程湖北省重点实验室，湖北 武汉 430070)

多维地震作用下高柔结构的地震响应*

魏文晖 黄玮松 薛广文 张迪

(武汉理工大学 道路桥梁与结构工程湖北省重点实验室，湖北 武汉 430070)

研究了水平、摇摆和竖向地震动耦合作用下高柔结构的地震响应.推导了水平、摇摆和竖向地震动耦合作用下的动力方程，方程中考虑了摇摆地震动导致的基础转角位移产生的附加重力二阶效应，并探讨了竖向地震作用对重力二阶效应的影响.以某210 m高的电视塔结构为原型，进行了水平、摇摆和竖向地震动耦合作用下的缩尺模型振动台试验.理论与试验结果对比表明：振动台试验结果与推导的动力方程理论分析结果基本吻合，验证了理论分析的合理性和准确性；竖向地震动不仅会引起常规的重力二阶效应的变化，对摇摆倾斜位移引起的附加重力二阶效应也有较大的影响；在水平、摇摆和竖向地震动耦合作用下，结构的动力响应与单一的水平地震作用相比，不仅几何刚度随时间变化，而且会导致较大的不对称的位移响应，使得原本满足水平地震作用下抗震需求的结构可能发生破坏甚至倒塌.

振动台实验；摇摆地震动；地震；高柔结构；动力响应

随着当代社会经济的高速发展，高柔结构以其独特的优点越来越受到欢迎.然而，高柔结构在计算地震响应时，为了简化计算，通常仅考虑水平地震作用[1-2](在一些特定条件下考虑竖向地震作用)，而忽略摇摆地震作用对其的影响[3].事实上，摇摆地震作用在震源附近对结构的影响是非常明显的，实例如表1所示.

很多结构的破坏甚至倒塌都与地震动中的摇摆分量有关，如1971年的San-Fernando地震中，水平和摇摆耦合地震作用导致桥梁垮塌.因此，包含摇摆分量的多维地震动对高柔结构的地震响应的影响已越来越受到国内外学者的重视[8-10].如李宏男等[11]将高层建筑和高耸结构简化成悬臂结构，建立水平和摇摆耦合作用下的运动平衡方程，得出随着结构的高度增加和刚度的增大，摇摆分量对结构地震响应的影响会显著增大的结论，并指出在高层和高耸结构设计时摇摆分量不可忽略.从现有文献和资料可以看出[12-15]，对于高柔结构的地震响应研究，国内外学者都不再局限于地震动水平分量的作用，开始逐步探讨地震动摇摆分量和竖向地震动对高柔结构地震响应的影响，并取得了一定的成果.但是，现有研究仍存在以下缺陷：地震动摇摆分量对高柔结构地震响应的影响的相关研究还仅仅局限于摇摆转角加速度的影响，忽视了摇摆倾斜位移产生的附加重力二阶效应；忽略了竖向地震动和摇摆地震动耦合作用时，竖向地震动对摇摆倾斜位移产生的附加重力二阶效应的影响.

表1 摇摆地震效应Table 1 Tilting ground motion effect

为此，文中推导了高柔结构在水平、摇摆和竖向地震动耦合作用下的动力方程，方程中考虑了竖向地震动对重力二阶效应的影响，以及摇摆转角位移产生的附加重力二阶效应.继而以某电视塔结构为原型，进行1∶100的缩尺比例模型振动台试验，对比试验和理论分析的结果，探究了高柔结构在地震动水平、竖向、摇摆转角加速度和摇摆倾斜位移耦合作用下的地震效应，为多维地震作用下高柔结构的抗震计算和设计方法提供依据.

1 多维地震作用下高柔结构的动力方程

水平地震作用下高柔结构体系的计算简图如图1所示，图1中Xi表示结构质点i对于地面的相对位移；βi表示质点i在结构变形后的割线转角，即质点i的相对位移和高度的比值；Hi表示质点i相对于地面的高度.

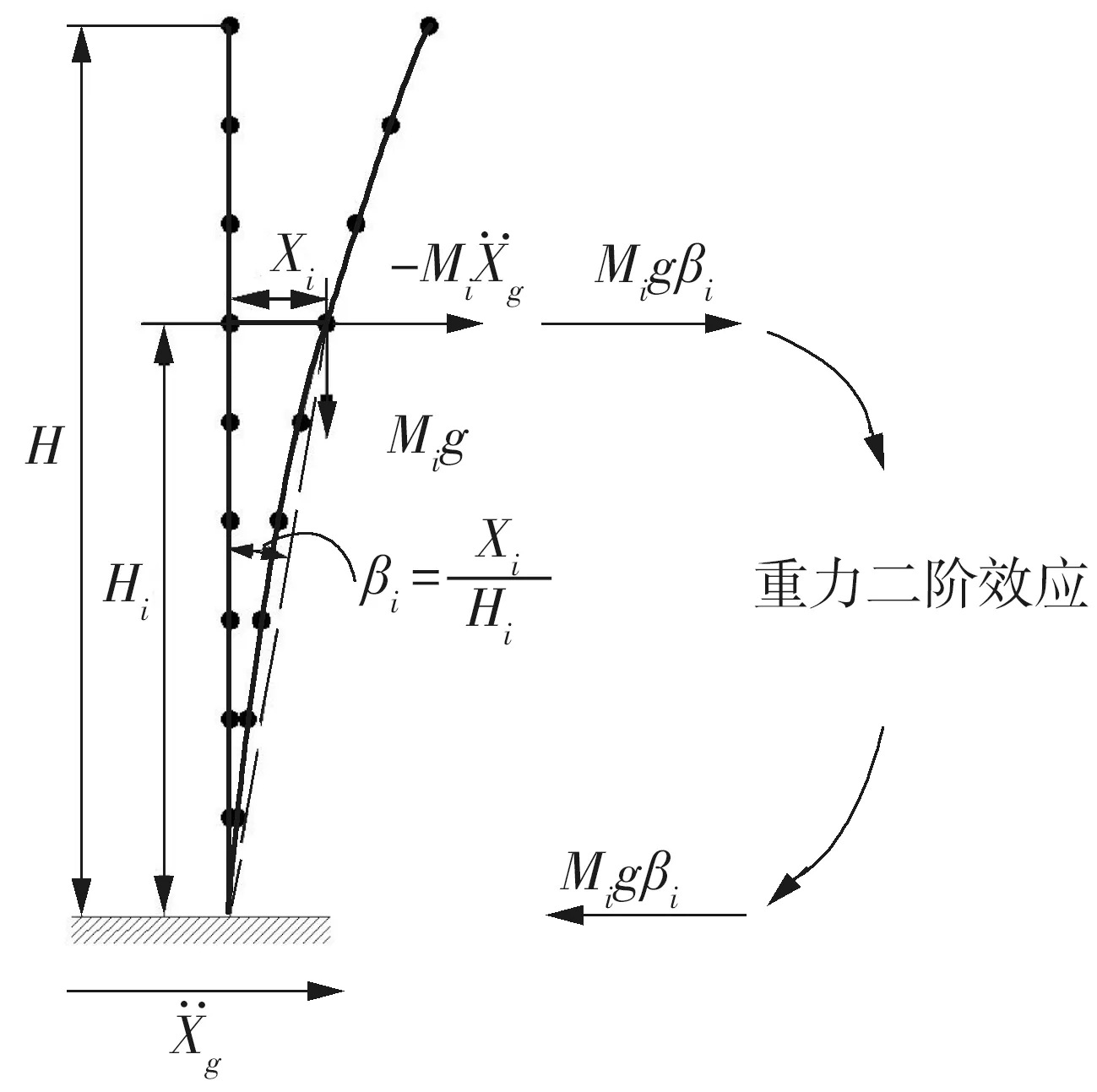
图1 水平地震动作用下多自由度体系示意图Fig.1 Multi-degree-of-freedom system under horizontal ground motion

水平地震动作用下高柔结构的动力方程为

(1)

式中，M、C、K0、KG和I分别表示结构体系的质量、阻尼、刚度、几何刚度和单位矩阵.质点i的重力二阶效应产生的附加弯矩可采用一对水平力产生的等效力偶表示(如图1所示)，即Migβi，因此，动力方程式(1)也可表示为

(2)

在水平和竖向地震动耦合作用下，考虑重力二阶效应，高柔结构水平位移的动力方程为

(3)

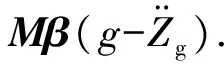
水平、摇摆和竖向地震动耦合作用下高柔结构体系的计算简图如图2所示，图中αg为摇摆地震动基础转角位移.

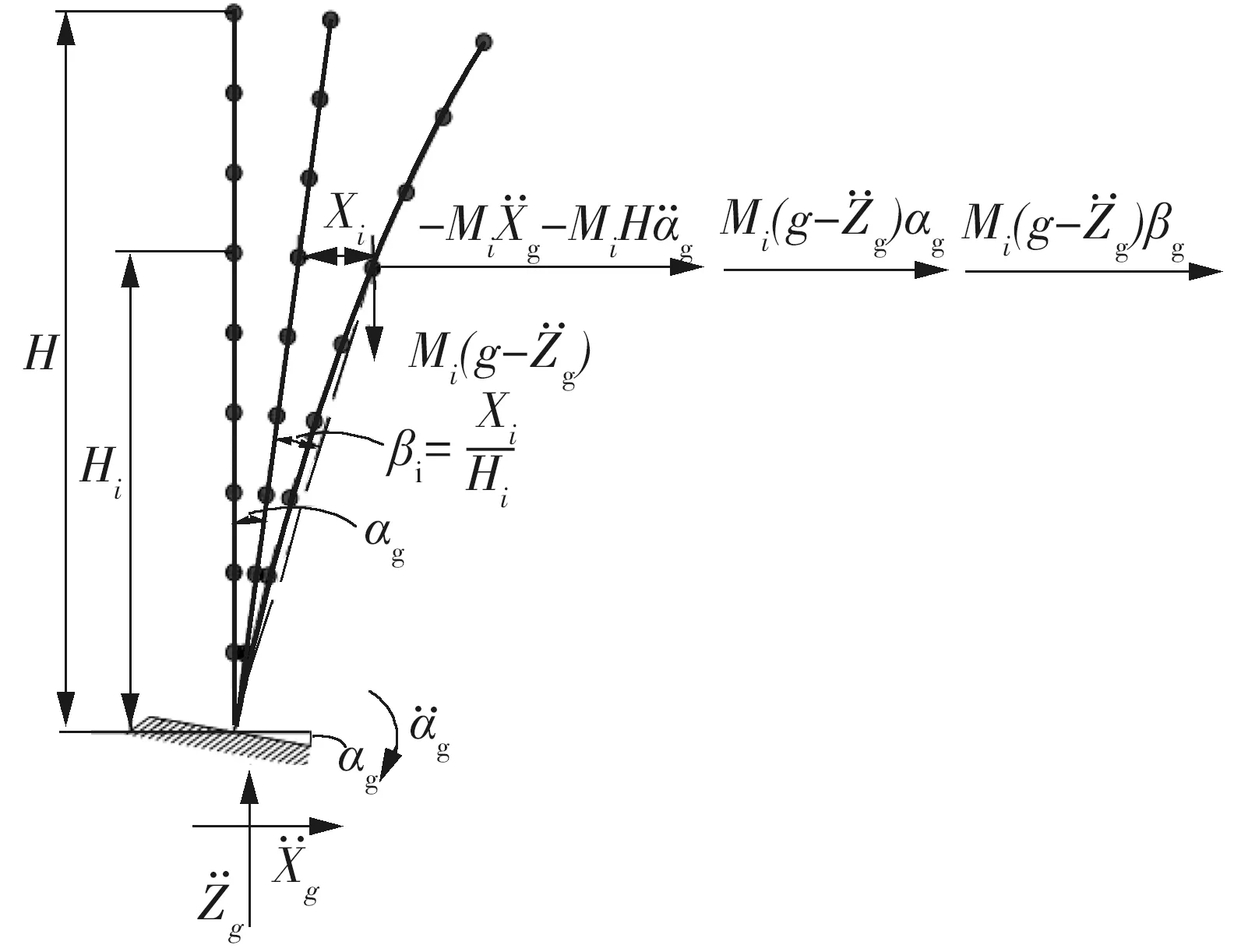
图2 多维地震作用下的多自由度体系示意图Fig.2 MDOF system under multi-component ground motion

在图2中，摇摆地震动基础转角位移使得高柔结构整体产生刚性偏移，导致结构产生附加重力二阶效应.此时，结构总的重力二阶效应由两部分组成，一部分是常规重力二阶效应分量Mβ(g-g)，与常规动力分析一样(方程(2)等式右边第二项)为几何刚度项的组成部分；另一部分是摇摆地震动基础转角位移产生的，不受结构地震响应的影响，应同其它地震动一样，以一个等效水平侧向力的形式出现在结构动力方程的激励项中，表示为MI(g-g)αg.结构体系的动力方程为

(4)

相较于水平和竖向地震动耦合作用下的动力方程(2)，方程(4)中增加了由摇摆转角位移αg产生的附加重力二阶效应，且该效应受竖向地震动影响.由于摇摆转角位移通常是非对称的[16]，将产生一定的残余倾斜位移，所以，此不对称的摇摆转角位移时程不仅会增大结构的重力二阶效应，而且还会使结构产生非对称的动力效应，对高柔结构的地震效应影响非常显著.

2 多维地震作用下高柔结构的振动台试验

振动台试验在重庆交通科研设计院的结构动力工程所完成.该工程所配备了国内先进的六自由度的振动台系统，台面尺寸为3 m×6 m，最大水平加速度为±3.0g，最大竖向加速度为±2.0g.

2.1 试验模型设计和拾振器布置

试验以某电视塔为原型，高为210 m，基本周期为3.1 s.按缩尺比例1∶100制作模型，相似常数见表2，试验照片如图3所示.

表2 试验模型的相似常数Table 2 Similarity parameters of test model

图3 试验模型照片Fig.3 Photo of experiment model

2.2 地震波选择

文中选取美国Pacoima大坝左上侧站点记录的Northridge地震波数据，未修正的地震动水平和竖向加速度时程如图4、5所示.

采用小波分析获取的地震动转角位移时程和加速度时程[16]，如图6、7所示.

2.3 试验工况

为研究竖向地震动和摇摆地震动对高柔结构的地震响应影响，文中设置了水平(H)，水平和竖向耦合(H-V)，水平和摇摆耦合(H-T)以及水平、摇摆和竖向耦合(H-T-V)4种工况.同时，试验中将水平地震波峰值调整为6.20 m/s2，即GB50011—2010 《建筑抗震设计规范》中9度罕遇地震时程分析时所采用的地震加速度峰值；竖向和摇摆地震波时程分别乘以相同的比例系数，再根据表2中试验模型的相似参数进行调整.振动台试验底面角位移由振动台试验底面输入地震动摇摆加速度分量时相应产生.

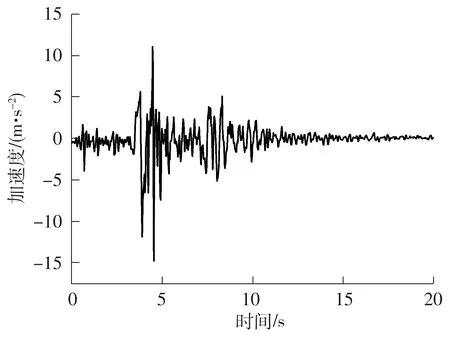
图4 Northridge地震水平加速度时程Fig.4 Time history of horizontal acceleration of Northridge earthquake

图5 Northridge地震竖向加速度时程Fig.5 Time history of vertical acceleration of Northridge earthquake

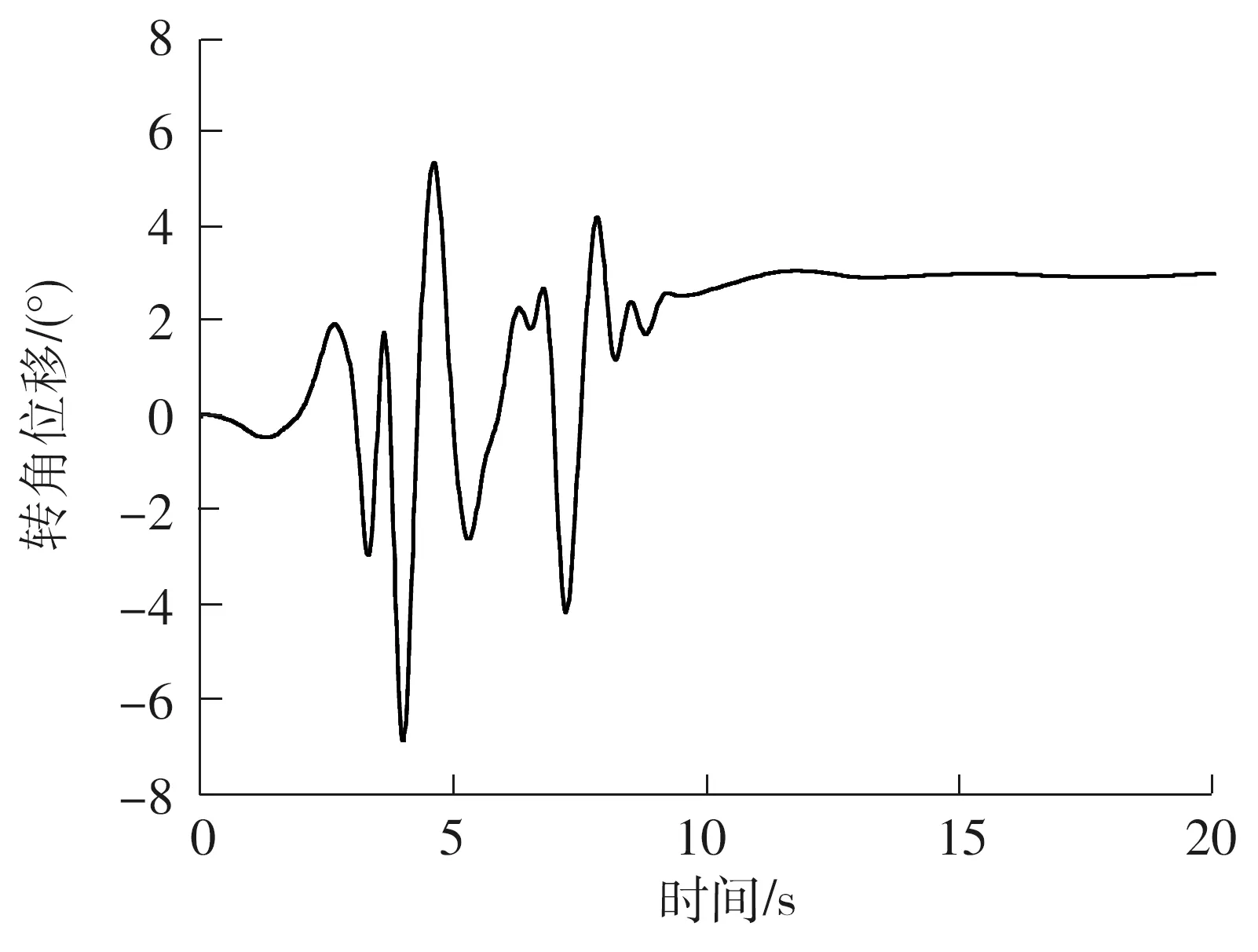
图6 摆倾斜位移时程Fig.6 Time history of tilting displacement

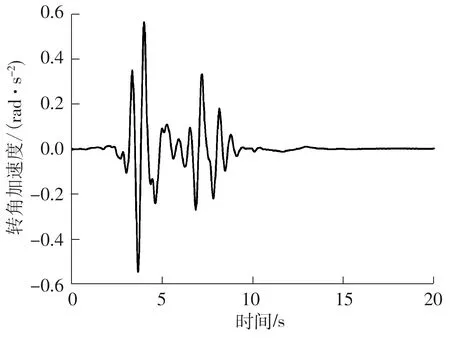
图7 Northridge地震摇摆转角加速度时程Fig.7 Time history of tilting acceleration of Northridge earthquake

2.4 试验结果

在实际的试验过程中，由于振动台设备等因素，各工况下每次试验台面的实际加速度时程和输入的加速度时程存在一定差异.因此在试验数据处理过程中，为了更合理地进行试验结果的对比，按各个工况相应地震波实际峰值的比值，对实验结果进行调整，使其皆为同等地震条件作用下的结果.

(1)动力特性

测得结构在白噪声工况下的地震响应，对它进行傅里叶变换，可以得到结构的基本周期为0.32 s，相应的阻尼比为2.1%.文中研究的电视塔结构基本周期为3.1 s，根据时间的相似常数可知，试验模型的理论基本周期应为0.31 s，与实际验模型的基本周期相近.

(2)加速度响应

振动台试验分别测得模型在水平(H)，水平和竖向耦合(H-V)，水平和摇摆耦合(H-T)，水平、摇摆和竖向耦合(H-T-V)工况下的加速度响应，其中幅值αmax和竖向地震动影响因子μ见表3，影响因子μ表示在水平和竖向耦合或水平、摇摆和竖向耦合工况下，竖向地震动导致的水平加速度幅值变化占水平或水平和摇摆耦合工况下水平加速度幅值的比重，以便探讨竖向地震动对水平以及水平和摇摆耦合作用下顶点加速度的影响.图8表示水平，水平和竖向耦合，水平和摇摆耦合以及水平、摇摆和竖向耦合作用下试验模型的顶点加速度时程曲线.

表3 水平加速度幅值和竖向地震动影响因子Table 3 Amplitude of horizontal acceleration and divisor of vertical ground motion

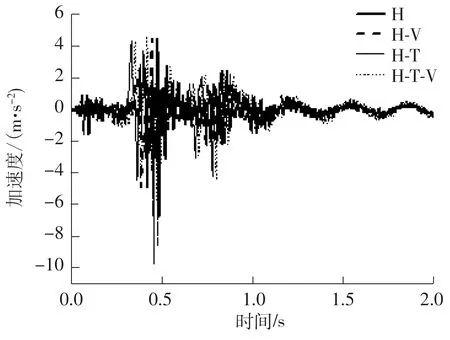
图8 H、H-V、H-T和H-T-V工况下的水平加速度时程Fig.8 Time history of horizontal acceleration under H,H-V,H-T and H-T-V conditions

从表3和图8可以看出：①水平和竖向耦合工况下，竖向地震动的影响因子为2.40%，说明竖向地震动的输入会增大结构的重力二阶效应，从而增大结构的水平加速度幅值，但是这种影响并不明显;②相较于水平工况，水平和摇摆耦合工况下结构的加速度幅值明显增大，增大幅度达到了43.67%，表明摇摆地震动对结构的加速度有较大的影响；③水平、摇摆和竖向耦合工况下，竖向地震动的影响因子达到了10.89%，说明在包含摇摆分量的多维地震作用下，竖向地震动的影响更加显著.

(3)位移响应

各工况下的位移幅值dmax和竖向地震动影响因子μ见表4，图9表示水平，水平和竖向耦合，水平和摇摆耦合以及水平、摇摆和竖向耦合工况下水平位移时程对比.

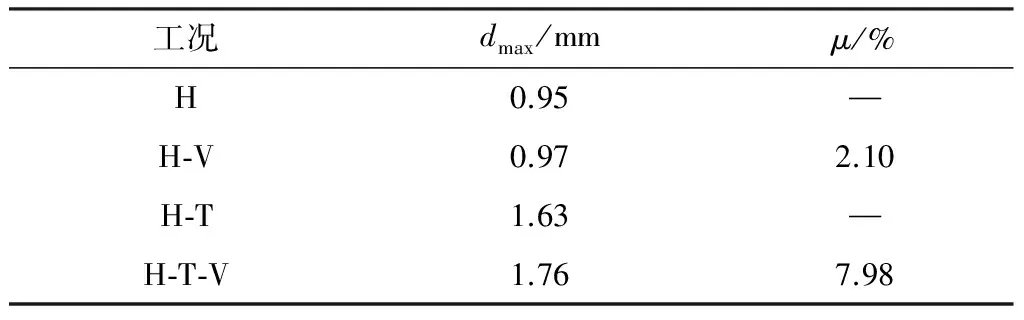
表4 水平位移幅值和竖向地震动影响因子Table 4 Amplitude of horizontal displacement and divisor of vertical ground motion

从表4和图9可以看出：水平和竖向耦合工况下，竖向地震动的影响因子为2.10%，说明竖向地震动也会增大结构的位移影响，但增大幅度不大，与加速度的变化情况类似；水平、摇摆和竖向耦合工况下竖向地震动影响因子达到了7.98%，同样说明了竖向地震动的输入会影响摇摆倾斜位移产生的重力二阶效应，从而较大幅度地增大了结构的位移幅值；与水平工况相比，水平、摇摆和竖向耦合工况下的水平位移幅值会显著增大，增幅为85.26%，且位移时程曲线发生了单侧偏移的不对称现象，说明摇摆地震作用不仅会大幅增大结构的平动响应，还将导致单侧偏移的不对称地震响应，使得原本抗震性能满足水平地震作用的结构发生破坏甚至倒塌.

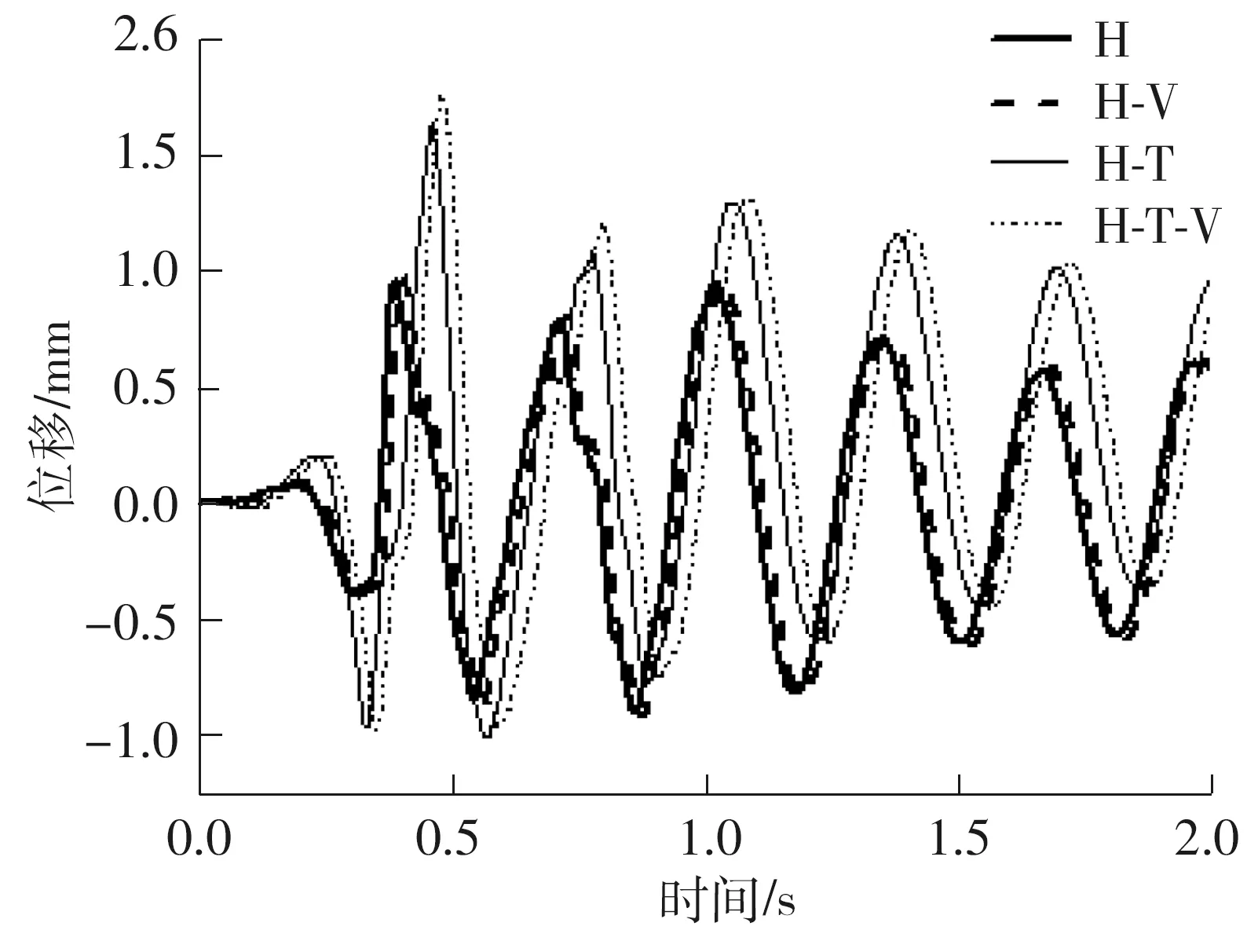
图9 H、H-V、H-T和H-T-V工况下的水平位移时程Fig.9 Time history of horizontal displacement under H,H-V,H-T and H-T-V conditions

3 试验与理论分析结果对比

为验证文中建立的水平、摇摆和竖向地震动耦合作用下高柔结构完整动力方程的合理性和准确性，以及附加重力二阶效应对结构地震响应的影响，将振动台实验和本文的理论分析方法进行对比.文中编写了考虑和不考摇摆倾斜位移产生的附加重力二阶效应(即动力方程(4)右边第4项MI(g-g)αg)的Matlab计算程序.为便于对比分析，考虑摇摆倾斜位移产生的附加重力二阶效应，在下文统称为理论分析1；忽略摇摆倾斜位移产生的附加重力二阶效应，在下文统称为理论分析2.为了使得理论分析得到的结果比较真实的还原模型的响应，理论分析所采用的各加速度时程为地震模拟振动台台面的实测数据.

(1)加速度时程对比

在各试验工况下，理论分析1、理论分析2和振动台试验的水平加速度幅值对比见表5，表中εa为各工况下，理论分析的水平加速度幅值与试验结果的相对误差.由于水平以及水平和竖向耦合工况没有输入摇摆地震波，所以不存在理论分析1和理论分析2之分.因篇幅限制，水平加速度时程对比图省略.

表5 水平加速度幅值对比Table 5 Comparison of amplitude of horizontal acceleration

从表5可以看出:水平工况与水平和竖向耦合工况下，理论分析和振动台试验结果的整体时程曲线的走势和波形基本一致，幅值的相对误差仅为5.37%和6.11%，说明建立的理论分析方法是合理的；在水平和摇摆耦合以及水平、摇摆和竖向耦合工况下，相较于理论分析2，理论分析1的水平加速度幅值和振动台试验的结果更为接近，相对误差均在6%左右，说明引入摇摆倾斜位移产生的重力二阶效应的理论分析方法更能够反应结构的真实地震响应，也证实了文中建立的水平、摇摆和竖向地震动耦合作用下的动力方程是合理和准确的.

(2)位移响应对比

在各试验工况下，理论分析1、理论分析2和振动台试验的顶层水平位移幅值见表6，表中相对误差εd表示各工况下，理论分析的水平位移幅值与试验结果的相对误差.图10、11分别表示水平和摇摆耦合以及水平、摇摆和竖向耦合工况下，水平位移时程对比.

从表6和图10、11可以看出：在各工况下，理论分析1的水平位移幅值和振动台试验的结果基本一致，相对误差控制在8%左右，而理论分析2的相对误差较大，相对误差最大可达到36.26%，进一步验证了文中建立的多维地震作用下高柔结构的动力方程是合理和准确的;在水平和摇摆耦合以及水平、摇摆和竖向耦合工况下，理论分析1和振动台试验得到的水平位移时程曲线均发生了单侧偏移的不对称现象，而理论分析2中这种现象不明显，说明不对称现象主要是由附加重力二阶效应导致的；振动台试验和理论分析1都揭示了，与单一水平地震作用相比，水平、竖向、摇摆转角加速度和摇摆倾斜位移耦合作用会导致一个完全不同的动态响应，水平位移幅值增大了约85%，且发生了单侧偏移的不对称现象.

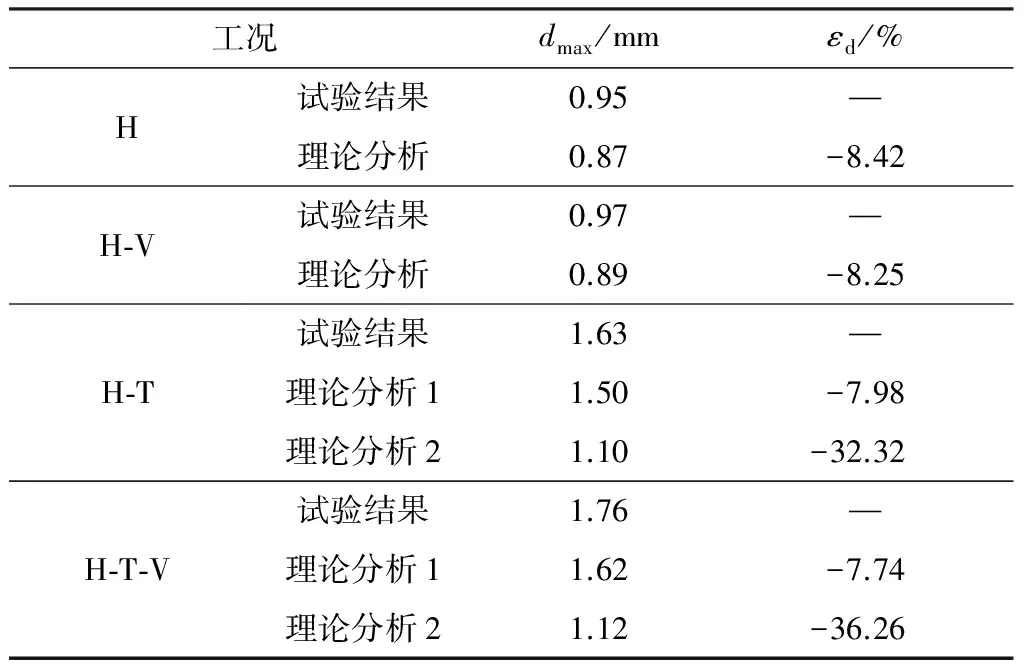
表6 水平位移幅值对比Table 6 Comparison of amplitude of horizontal displacement

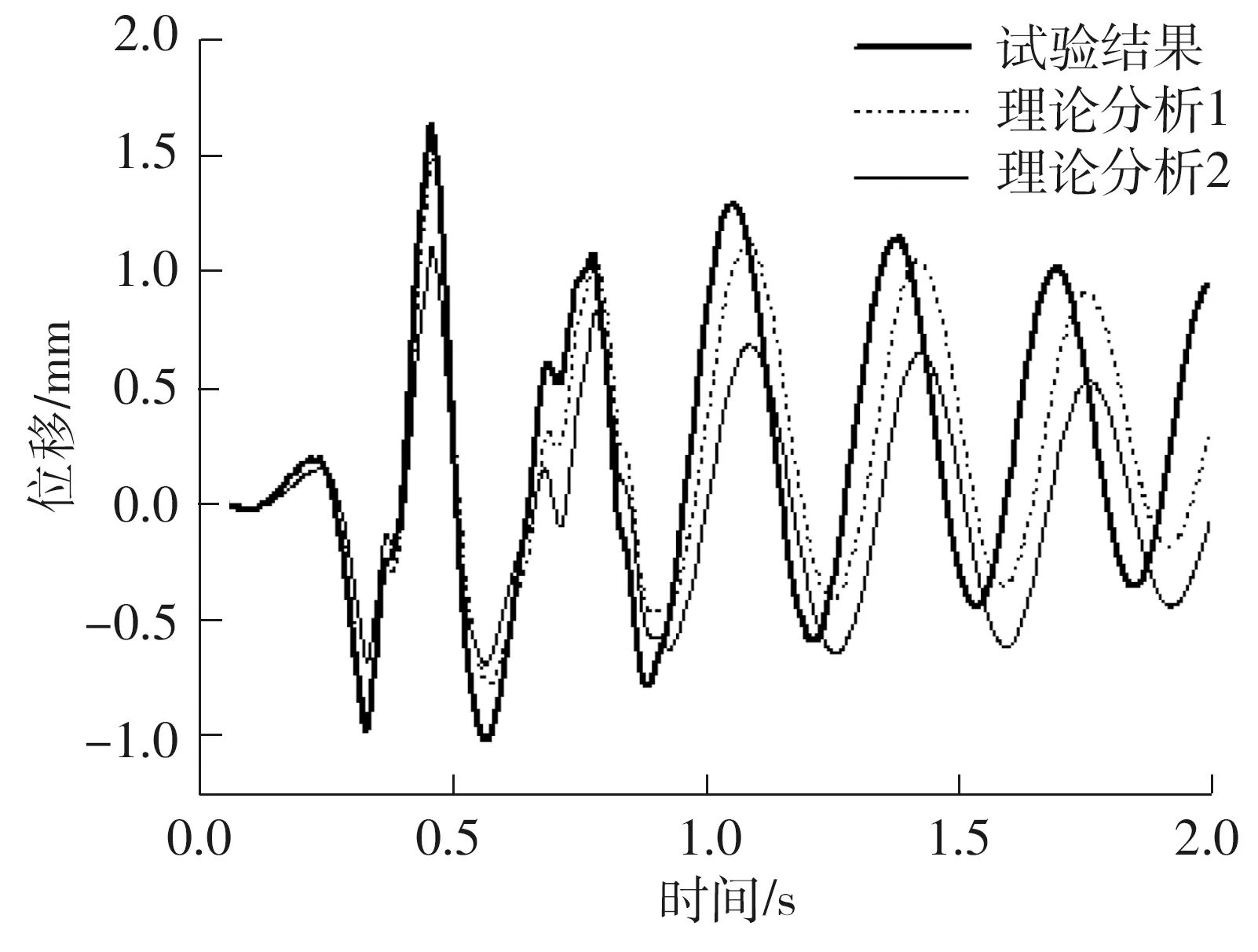
图10 H-T工况的水平位移时程对比Fig.10 Comparison of horizontal displacement under H-T condition

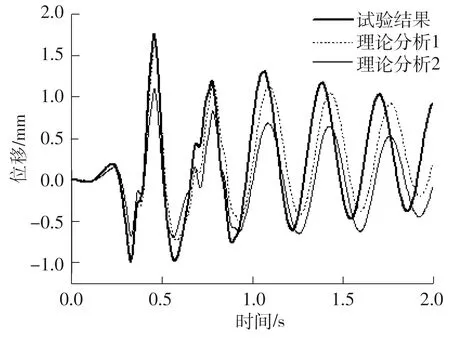
图11 H-T-V工况下的水平位移时程对比Fig.11 Comparison of horizontal displacement under H-T-V condition

另外，由于文中采用美国Northridge1994年Pacoima站点的地震时程，该站点摇摆地震动幅值和震后地面残余倾斜较大(3.1°)，因此，分析结果中摇摆地震动的影响也较为显著.

4 结论

文中推导了水平、摇摆和竖向地震动耦合作用下的动力方程，考虑了摇摆地震动基础转角位移产生的附加重力二阶效应，以及竖向地震作用导致几何刚度的变化，理论与试验对比分析表明，所推导的动力方程是合理和准确的.

水平、摇摆和竖向耦合工况下竖向地震动位移影响因子达到了7.98%，高于水平和竖向耦合工况下的2.10%，说明竖向地震动的输入将影响摇摆倾斜位移产生的重力二阶效应，从而较大幅度地增大了结构的位移幅值.

在水平、摇摆和竖向地震动耦合作用下，结构的动力响应与单一的水平地震作用相比，不仅几何刚度随时间变化，而且会导致较大的非对称的位移响应，使得原本满足水平地震作用下抗震性能的结构发生破坏甚至倒塌.

[1] 杨红，任小军，徐海英.双向水平地震下时程分析法中输入波的选择 [J].华南理工大学学报(自然科学版)，2010，38(11)：40-46.

YANG Hong,REN Xiao-jun,XU Hai-ying.Selection of input waves in tine-history analysis under bi-direction hori-zontal seismic action [J].Journal of South China University of Technology(Natural Science Edition),2010,38(11):40-46.

[2] 杨春，潘健明，蔡健,等.框架-核心筒超限高层结构的抗震性能评估 [J].华南理工大学学报(自然科学版)，2013，41(6)：84-90.

YANG Chun,PAN Jian-ming,CAI Jian,et al.Evalution of seismic performances of super high-rise frame-core wall structure [J].Journal of South China University of Technology(Natural Science Edition),2013,41(6):84-90.

[3] 李宏男.关于地震动转动分量的研究 [J].沈阳建筑工程学院学报(自然科学版)，1991，7(1):88-93.

LI Hong-nan.Study on rotational components of ground motion [J].Journal of Shenyang Architectural and Civil Engineering Institute(Natural Science Edition),1991,7(1):88-93.

[4] GRAIZER V.Coupled tilt and translational ground motion response spectra [J].Journal of Structural Engineering,2007,133(5):609-619.

[5] GRAIZER V.Tilts in strong ground motion [J].Bulletin of the Seismological Society of America,2006,96(6):2090-2102.

[6] 彭小波，李小军.汶川地震强震动地面倾斜研究 [J].地震学报，2012，34(1)：64-75.

PENG Xiao-bo,LI Xiao-jun.Study of ground surface tilts from strong motion records of the Wenchuan earthquake [J].Acta Seismologica Sinica,2012,34(1):64-75.

[7] GHAZVINI T T H R N.Seismic response of aboveground steel storage tanks:comparative study of analyses by six and three correlated earthquake components [J].Latin American Journal of Solids and Structures,2013,10(6):1155-1176.

[8] TRIFUNAC M D.The role of strong motion rotations in the response of structures near earthquake faults [J].Soil Dynamics & Earthquake Engineering,2009,29(2):382-393.

[9] 李宏男，孙立晔.地震面波产生的地震动转动分量研究 [J].地震工程与工程振动，2001，21(1):15-21.

LI Hong-nan,SUN Li-ye.Rotational components of earthquake ground motions derived from surface waves [J].Earthquake Engineering and Engineering Vibration,2001,21(1):15-21.

[10] 魏文晖，张迪，喻梦,等.带悬吊质量结构的多维地震反应 [J].哈尔滨工业大学学报，2014，46(4):98-104.

WEI Wen-hui,ZHANG Di,YU Meng,et al.Seismic response of structure with suspended mass [J].Journal of Harbin Institute of Technology,2014,46(4):98-104.

[11] 李宏男，王苏岩，周健.在水平与摇摆地震动联合作用下高层与高耸结构随机反应分析 [J].土木工程学报，1991，24(1)：44-50.

LI Hong-nan,WANG Su-yan,ZHOU Jian.Random response analysis of tall buildings and highrise structure under combined action of horizontal and rocking ground motions [J].China Civil Engineering Journal,1991,24(1):44-50.

[12] GRAIZER V,KALKAN E.Prediction of spectral acceleration response ordinates based on PGA attenuation [J].Earthquake Spectra,2009,25(1):39-69.

[13] LI Hong-nan,SUARE E,SINGH P.Rotational components of earthquake ground motion [J].Earthquake Engineering and Engineering Vibration,1997,17(2):37-51.

[14] FALAMARZ-SHEIKHABADI M R.Simplified relations for the application of rotational components to seismic design codes [J].Engineering Structures,2014,59(2):141-152.

[15] ELNASHAI A S,PAPAZOGLOU A J.Procedure and spectra for analysis of RC structures subjected to strong vertical earthquake loads [J].J of Eq Eng,2012,1(1):121-155.

[16] 魏文晖，薛广文，张迪,等.基于小波分析的地震动转动分量研究 [J].岩土工程学报，2015，37(7)：1241-1248.

WEI Wen-hui,XUE Guang-wen,ZHANG Di,et al.Rotational components of ground motion based on wavelet analysis [J].Chinese Journal of Geotechnical Engineering,2015,37(7):1241-1248.

s:Supported by the National Natural Science Foundation of China(51178362，51678462)

SeismicResponseofHigh-FlexibleStructureUnderMulti-componentGroundMotion

WEIWen-huiHUANGWei-songXUEGuang-wenZHANGDi

(Hubei Key Laboratory of Roadway Bridge and Structure Engineering, Wuhan University of Technology, Wuhan 430070, Hubei, China)

In this paper, the seismic response of the high-flexible structure under coupled horizontal, tilting and vertical ground motion is investigated. First, a dynamic equation under the coupled ground motion is derived, in which the additional second-order effects of gravity caused by the foundation tilt under the tilting ground motion is taken into consideration. Then, the influence of the vertical ground motion on the second-order effects of gravity is discussed. Finally, by taking a 210 m television tower as the prototype, the shaking table test of a reduced scale model is carried out under the coupled ground motion. The comparison between the theoretical analysis results and the test ones show that (1) the results of the shaking table test accord well with the theoretical ones obtained through the derived dynamic equation, which testifies the rationality and accuracy of the theoretical analysis; (2) the vertical ground motion can cause the change of the conventional second-order effects of gravity to change, and it has an significant impact on the additional second-order effects of gravity caused by the tilt; and(3)as compared with the single horizontal ground motion, the coupled ground motion causes the geometric rigidity to change with time and results in a larger asymmetric displacement, which means that the structure capable of resisting the horizontal ground motion originally may get destroyed.

shaking table test; tilting ground motion; earth quake; high-flexible structure; dynamic response

2016-12-14

国家自然科学基金资助项目(51178362，51678462)

魏文晖(1963-)，男，教授，主要从事结构抗震设计研究.E-mail:weiwenhui@whut.edu.cn

1000-565X(2017)08-0103-07

TU 317

10.3969/j.issn.1000-565X.2017.08.015