线性回归模型结构稳定性检验的实证分析
2018-01-10黄艳华
黄艳华
(重庆师范大学涉外商贸学院 数学与计算机学院,重庆 401520)
线性回归模型结构稳定性检验的实证分析
黄艳华
(重庆师范大学涉外商贸学院 数学与计算机学院,重庆 401520)
线性回归模型分析时间序列数据可能出现模型结构稳定性的问题.在线性回归模型结构稳定性Chow检验方法的基础上探讨了Quandt-Andrews 检验,并通过模拟序列,利用Eviews 8.0软件对两种检验方法进行了实证对比分析.研究发现,Quandt-Andrews 检验具有较高的检验效度.
结构稳定性;Chow检验;Quandt-Andrews检验;Eviews 8.0
0 引言
模型具有较高的预测与分析功能是建模的目的之一.回归分析构成计量经济学的方法论基础,建立回归模型时经常希望模型的参数具有稳定性,即模型的结构不变.然而,随着经济的发展,经济结构的变化往往导致计量模型结构也发生变化.因此,为了揭示真实的经济关系,除了对模型做变量的显著性检验、拟合优度检验和方程的显著性检验之外,还需要对模型进行结构稳定性检验.
一些学者,如李均立[1]、王淑超[2]、黄祖辉和陈林兴[3]、江海峰[4]、杨海文和王丹华[5],利用Chow检验方法对线性回归模型的结构稳定性进行了研究.然而,另一种具有较高检验效度的方法:Quandt-Andrews分割点检验却很少被学者使用.
本文首先给出线性回归模型结构稳定性的含义,其次简要介绍Chow检验,以及Quandt-Andrews检验的原理,最后利用Eviews 8.0软件,通过模拟序列对两种检验方法进行实证对比分析.
1 线性回归模型结构稳定性的涵义
线性回归模型的结构稳定性最直观的理解为,对于时间序列数据进行建模分析时,采用不同时间段的数据所建立的模型的截距项和回归系数相等.
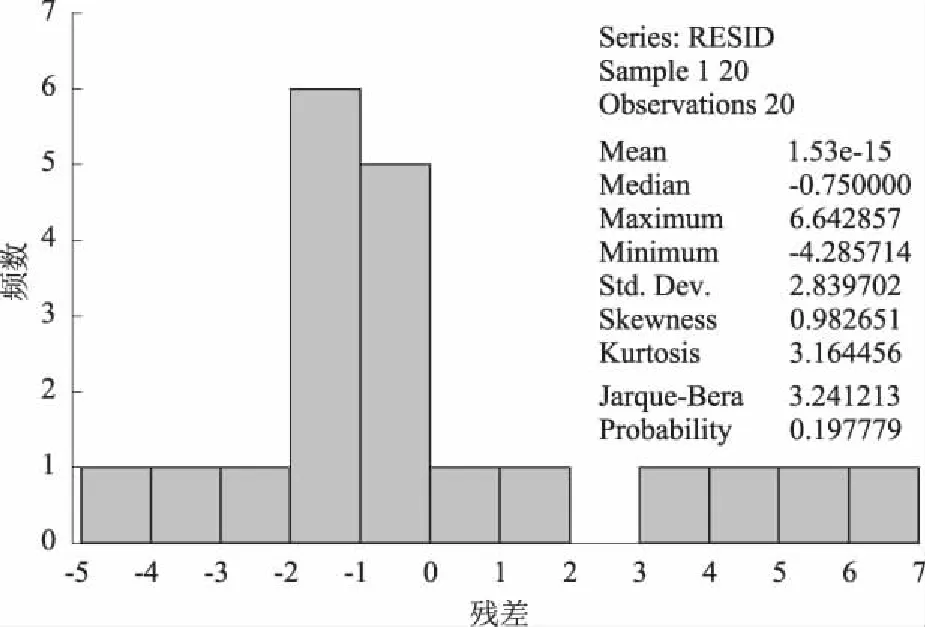
设定两个变量Y,X,其中X为自变量,Y为因变量.时间序列数据为Yt,Xt,t=1,2,…,n,把数据分为两组,前n0(n0 (1) (2) Y=β0+β1X1+β2X2+…+βkXk+μ. (3) 模型的结构稳定性检验的步骤如下. 第一步:提出原假设,备择假设. 第二步:构造检验统计量. 第三步:根据样本数据,计算检验统计量的值,确定拒绝域. 如何构造适当的检验统计量检验模型的结构稳定性是下面行文的出发点与最终要实现的目标. Chow分割点检验是检验两个或多个线性回归方程中系数之间是否存在“等量性”的最为基本和常用的检验方法.Chow分割点检验方法的思路为:利用不同时间段的数据,建立回归方程,利用残差平方和构造F统计量,并确定拒绝域,其具体步骤如下. 第一步:用OLS方法分别对模型(1)、(2)、(3)进行参数估计,并求得残差平方和分别为RSS1、RSS2、RSS. 第二步:构造F统计量, 其中k为解释变量的个数. 第三步:确定拒绝域. 如果模型不具有结构稳定性,则RSS-(RSS1+RSS2)的差异较大,计算的F值也较大.利用样本数据计算F统计量的值,并将其与所给定显著性水平下的临界值进行比较,进而给出检验的结果. 在Chow检验的Eviews实施中,需要手动输入分割点的时间,但是当分割点不确定或未知时,Chow检验的应用不免有一定的局限性.Chow分割点检验需要在分割点已知的情况下,才能实现其检验的经济意义.然而,一般情况下分割点是未知的,为了克服Chow检验的局限性,Quandt与Andrews提出了一种检验方法,即Quandt-Andrews 分割点检验. Quandt-Andrews分割点检验[6]是检验某种设定形式下的方程是否存在一个或多个未知的结构突变点,这种检验基于Chow分割点检验.如果想要分析包含了k个样本点的两个时间点或在观测值区间(τ1,τ2)上是否存在结构变化,Chow检验需要在每个观测点处分别进行检验,其检验过程比较复杂.而Quandt-Andrews分割点检验将通过Chow检验得到的k个检验统计量汇总成一个统计量,并利用数理统计的方法,来检验原假设H0:在(τ1,τ2)的时间段上不存在结构突变点. Quandt-Andrews分割点检验中涉及的统计量有最大统计量、Ave统计量、Exp统计量,其相应表达式分别为 以下通过构造一个出现突变点的线性回归序列,运用Eviews 8.0软件,利用Chow检验和Quandt-Andrews检验方法对此线性回归模型的结构稳定性进行实证对比分析.假设其中μt是服从标准正态分布的序列.具有结构突变的线性回归序列为 (4) 从(4)式可以看出在10~11点处数据出现了突变.忽略这种突变,利用所有的数据做线性回归分析,分析结果为表1,并根据表1的结果给出估计方程 t. (5) 由表1可知,统计量R2=0.932 6,调整的R2=0.928 9,即具有较高的拟合优度,F统计量的值为249.125 9,从F统计量的P值,可以看出模型整体拟合效果是显著的.然而这个模型是利用发生结构变化的数据生成的,在忽视模型发生结构突变的条件下,直接回归,这样做出来的结果不具有任何经济意义.由D.W.量的值为0.593 1知,模型的残差存在序列相关. 由图1可知,模型的残差在第11个样本点之前逐渐增大,在第11个样本点之后骤然变小,因此第11个样本点是结构突变点.由图2可知,模型的残差的偏度值0.982 651>0,具有负偏离(也称左偏态),因此模型(5)不满足古典线性回归模型的基本假设,从而模型(5)是虚假回归. 图1 残差序列图Fig.1 Residual sequence diagram 图2 残差序列的正态性检验 Fig.2 Normality test of residual sequence 由前文的分析可知,模型在第11个样本点处发生了结构突变.然而,一般情况下进行回归分析前是无法确定结构突变点的位置的.为了深入理解Chow检验和Quandt-Andrews 检验方法以及检测两种方法的检验效度,下文的检验是在结构突变点未知的条件下进行的. 模型(5)的 Chow 分割点检验:在结构突变点未知的条件下,尝试输入分割点9、10、11,检验结果为表2.由表2可知,在5%的显著性水平下,Chow检验拒绝在9、10、11没有发生结构突变的假设.而由前文的分析可知,模型实际是在第11个样本点处发生结构突变.因此,结合本文的实例,在结构突变点未知的情况下,采用Chow分割点检验,检验的准确性有待提高. 模型(5)的 Quandt-Andrews 分割点检验:在结构突变点未知的情况下,Quandt-Andrews 分割点检验可以直接进行,检验结果如表3.由表3中最大似然F统计量和最大沃尔德F统计量可知,第11个样本点为模型的结构突变点,检验结果与实际情况相符合. 表2 Chow 分割点检验Tab.2 Chow split point test 为了提高线性回归模型的预测与分析功能,避免虚假回归现象的出现,或为了准确地揭示经济现象之间的关系,在建模的过程中需要对模型进行结构稳定性检验.在Chow检验的Eviews实施中,需要手动输入分割点的时间,但是当分割点不确定或未知时,Chow检验的应用不免有一定的局限性;在Quandt-Andrews 检验的Eviews实施中,即使在结构突变点未知的情况下,其检验也可以直接进行. 本文在简要介绍Chow检验以及Quandt-Andrews检验原理的基础上,通过模拟序列对两种检验方法进行实证对比分析.研究发现,在结构突变点未知的情况下,Chow检验的结果与实际情况不符,而Quandt-Andrews检验结果与实际情况相符合.因此,相对于Chow检验,Quandt-Andrews检验的结果更可靠,检验效度更高. [1] 李均立.线性回归模型结构稳定性的Eview 诊断[J].技术经济与管理研究,2009(1):10-12. [2] 王淑超.线性回归模型结构稳定性检验方法及其比较[J].巢湖学院学报,2016,18(3):1-5. [3] 黄祖辉,陈林兴.浙江农村居民消费支出系统函数的稳定性检验[J].浙江大学学报(人文社会科学版),2009,40(3):20-31. [4] 江海峰.回归系数稳定性的检验及实证分析[J].知识丛林,2005(11):126-127. [5] 杨海文,王丹华.线性回归模型参数检验方法的对比分析[J].井冈山大学学报(自然科学版),2011,32(5):24-28. [6] 高铁梅.计量经济分析方法与建模[M].北京: 清华大学出版社,2009:85-86. EmpiricalAnalysisofLinearRegressionModelStructuralStabilityTest HUANG Yanhua (SchoolofMathematicsandComputerScience,ChongqingNormalUniversityForeignTradeandBusinessCollege,Chongqing401520,China) Linear regression model analysis of time series data may present the problem of structural stability of the model.Based on the Chow test method of linear regression model, the Quandt-Andrews test was explored, and the Eviews 8.0 software was used to simulate the two methods. The Quandt-Andrews test was found to have higher test validity. structural stability; chow test; Quandt-Andrews test; Eviews 8.0 2017-09-09 黄艳华(1990—),女,河南周口人,重庆师范大学涉外商贸学院数学与计算机学院教师. 10.3969/j.issn.1007-0834.2017.04.007 F224.0 A 1007-0834(2017)04-0029-04

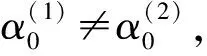
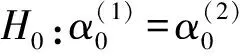
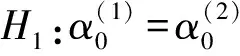
2 Chow分割点检验
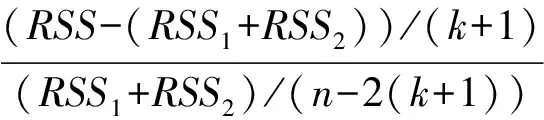
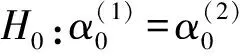
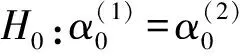
3 Quandt-Andrews分割点检验
4 两种检验方法的实证对比分析
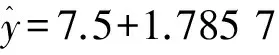


5 结束语
