冷轧铝带卷取内部应力有限差分仿真研究

张波，王伟,2，李世苗

（1. 福州大学 机械工程及自动化学院，福州 350100；2. 福建省高端装备制造协同创新中心，福州 350100）

冷轧铝带卷取内部应力有限差分仿真研究

张波1，王伟1,2，李世苗1

（1. 福州大学 机械工程及自动化学院，福州 350100；2. 福建省高端装备制造协同创新中心，福州 350100）

目的 研究冷轧铝带卷取内部应力的分布情况以及影响因素，为铝带卷筒的设计提供参考。方法 通过冷轧铝板压缩实验，测定铝带径向压缩系数与应力的关系曲线；采用非线性有限差分法对卷取过程和内部应力进行仿真；分析线性、一次非线性和二次非线性材料模型以及卷筒刚度对带卷内部应力分布的影响。结果 径向压缩系数的理论值与实验值有较好的一致性，卷筒刚度对铝带卷内层应力影响较大，而对外层影响很小，卷筒刚度较小时，在卷芯处容易产生塌卷缺陷，卷筒刚度较大时，容易出现扁卷现象。结论 计算带卷内部应力分布时，需要考虑铝带卷的各向异性以及层与层之间的紧密程度，合理选择卷筒的刚度对提高卷取质量有很大的实际意义。

冷轧铝带；有限差分法；径向压缩系数

铝带卷取是带逐层卷到卷筒上的过程，涉及带与卷筒之间以及带层之间的接触[1—2]。卷取过程不仅会在卷筒上施加很大的压力，影响卷筒的使用；而且随着卷取层数的增加，带卷内部会发生复杂的应力应变变化。带卷内部应力分布不合理会造成卷芯塌陷、扁卷、层间滑移等缺陷[3—6]，因此，铝带卷取过程中内部应力的研究不但能揭示卷取过程中的力学现象，而且将为铝带卷筒的选择提供参考。

铝带的卷取过程是一个高度非线性的过程，涉及材料非线性、几何非线性以及接触非线性[7]。对工程上大多数非线性问题，很少可直接利用解析法获得其解，少数情况可利用简化假设来求解，但是过多的假设可能导致结果不正确甚至错误的解，因此数值解是一个好的替代方法，有限差分和有限元方法是两种常用的数值计算方法[8—11]。燕山大学的李海亮利用有限元软件ANSYS/LS-DYNA，建立了冷轧卷取过程实体模型，对卷取过程进行动态模拟仿真分析，得出在卷取过程中张力分布规律[12]。常铁柱等人在现场实测紧密系数实验的基础上，通过卷取过程应力场的差分求解以及卷取结束后卸卷过程中机械应力和热应力耦合应力场的差分法求解，获得了钢卷内部应力场的分布规律[13]。

为研究铝带卷取过程中带卷内部应力分布情况以及影响因素。文中利用有限差分法对铝带卷取过程中带卷内部应力进行了数值仿真，分析了线性、一次非线性和二次非线性材料模型以及卷筒刚度对带卷内部应力分布的影响。

1 冷轧铝带径向压缩系数

铝带卷曲的径向变形除了一般的弹性形变外，还应考虑层间粗糙面接触引起的附加压缩变形，所以引入了铝带径向压缩系数概念。紧密系数m是材料弹性模量E与径向压缩系数Er的比值，其值取决于带材表面的粗糙度、压力以及厚度，所以确定m就需要知道径向压缩系数Er。下面通过实验和理论对Er的值进行研究。

铝带径向压缩系数的测定采用电子万能试验机CMT5305，最大的试验力为300 kN，精度为1级。压板采用淬火轴承钢Φ150 mm，试验对象取某厂0.38 mm规格的1050铝合金，尺寸为130 mm×130 mm，取 160层。通过试验得到的数据为压力-位移的关系曲线，转换为应力-应变曲线，其斜率为径向压缩系数Er，由此可得到层叠板的径向压缩系数与应力之间的关系。

根据文献[14]所述，径向压缩系数的计算公式为：

式中：h为铝带的平均厚度；k0为修正系数，一般取0.3～0.6，这里取为0.45；Δ为铝带材接触表面不平度的最大值，这里取为5.87 µm；p为加载压力；E为铝带的弹性模量。

由式(1)可知，径向压缩系数Er的值与压力和厚度成正比关系，与表面不平度成反比。将板叠压缩试验中的压力实测值代入式(1)，可得径向压缩系数与应力的关系，径向压缩系数的理论值与实验实测的对比见图1，可以看出，两者有较好的一致性，但存在一定误差。

图1 径向压缩系数的理论值与实验实测的对比Fig.1 Comparison between theoretical value of radial compression coefficient and experimental measurement

2 铝带卷取平面轴对称有限差分模型

2.1 铝带卷内部应力解析模型

根据卷取机的实际工作情况来看，铝带是逐层缠绕在卷筒上的，分析模型见图2。当卷取完成时，将每层带材的径向压力增量在径向方向进行叠加，即可得到铝带卷层间压力随径向的变化，同样，求得每层带材切向应力增量后，也可求得切向应力沿径向分布。在卷取半径为r的单层铝带时产生的压力称为压力增量，用δp来表示。

图2 卷取解析模型Fig.2 Coiling analysis model

由文献[15]知，用压力增量表示的微分方程为：

压力增量满足两个边界条件：① 最外层压力增量与卷取张力满足式(3)；② 铝带卷内表面径向位移满足连续性条件，即带卷内部径向位移等于卷筒径向位移，即式(4)。

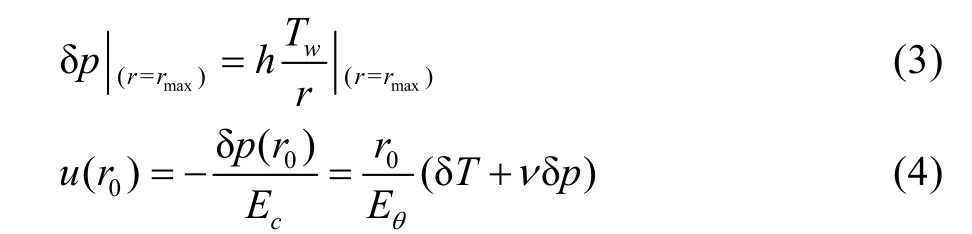
式中：rmax为铝带卷外径；Ec为卷筒径向刚度；r0为铝带卷内表面半径，即为卷筒外表面半径；δT为带卷内部切向应力增量；ν为铝带泊松比；Tw为张力；Eθ为铝带切向弹性模量。

根据不考虑剪切时用极坐标表示的平衡方程，可得到每层铝带切向应力增量方程式(5)。

式(2), (3)和(4)组成了卷取单层铝带时求解径向压力增量的边值求解模型，求解出铝带卷每层的径向压力增量后，再根据式(5)可得到切向应力增量。

2.2 有限差分法列式

假设铝带卷共有N层，则卷取第i层时的内表面半径ri为在半径ri处，由卷取N+1层引起的压力增量用δpi表示。将径向压力的一阶与二阶基本差分方程代入式(2)中，得径向压力增量的差分方程(6)。

边界条件的差分方程分别为：

求解方程组可得每层铝带的径向压力增量，利用以下叠加公式得到沿半径方向分布的铝带卷内部径向压力与切向应力。

式中：δpij为第i层由于第j层卷取产生的径向压力增量；δTij为第i层由于第j层产生的张力增量。

2.3 铝带卷材料模型和有限差分求解

铝带卷为各向异性材料，径向压缩系数由于卷取的紧密程度不同而与切向弹性模量不相等。根据实验所得的径向压缩系数与压力的关系曲线，可得到一次和二次拟合方程式。

某四辊铝带冷轧卷取机Ec=61 MPa/mm，卷筒外径为r0=332 mm。轧件设定张力Tw=35 MPa，铝带板厚h=0.72 mm，切向弹性模量Eθ=77 GPa，泊松比ν=0.33，共卷取1000层。有限差分计算流程见图3，利用MATLAB[16—17]编制计算程序。

图3 差分法计算铝带卷内部应力流程Fig.3 Flow chart for calculating internal stress of aluminum coil with difference method

3 铝带卷内部径向压力和切向应力结果分析

3.1 铝带卷内部应力分布规律

由以上工况计算铝带卷内部应力分布情况，图4为考虑径向压缩系数Er为一次拟合时的带卷内部径向压力与切向应力的分布，可得到如下规律。

带卷内层径向压力最大，层间径向压力随卷径增大而减小，中部区域变化较为平缓，最外层为自由表面，其径向压力为0，在铝带卷内部区域与外部区域径向压力沿半径方向下降较快，而中部区域变化较为平缓。带卷内部切向应力较大，随后减小，在外层一定区域开始再次增大，最外层切向应力与卷取张应力相等，在带卷中部区域切向应力出现负值，表明带卷出现张力松弛，这与实际经验相符。从图4还可看出带卷内层径向压力最大，对卷筒强度影响较大；外部区域径向压力较小，开卷时有滑移的趋势。

3.2 材料模型对内部应力的影响分析

图5为线性材料、一次非线性和二次非线性3种情况下的铝带卷径向压力与切向应力分布情况，从这些分布情况可得出，线性材料模型计算出的径向压力值以及切向应力值均比非线性模型结果要大得多，这是由于线性模型虽然考虑了铝带卷的各向异性特性，但没有考虑铝带卷层与层之间的紧密程度对内部应力分布的影响。两种非线性模型的计算结果基本接近，说明对径向压缩系数采用一次非线性拟合就足够了。

图4 铝带卷应力分布Fig.4 Stress distribution of aluminum coil

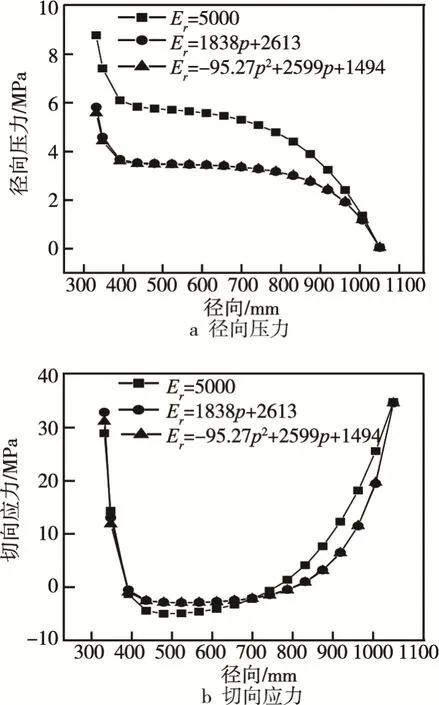
图5 材料模型对铝带卷压力的影响Fig.5 Influences of material model on stress of aluminum strip

3.3 卷筒刚度对内部应力的影响分析

卷筒作为铝带卷取的支撑机构，其刚度对铝带卷应力分布影响很大。现研究卷筒刚度Ec分别取5, 28,61 MPa/mm时，铝带卷应力分布的不同。从图6可以看出，卷筒刚度对铝带卷内层应力影响很大，而对外层影响很小，且外层几乎按相同曲线变化。卷筒刚度较小时，虽然可以降低卷芯处的径向压力，但切向应力却变成压缩应力，此时卷芯处容易产生塌卷缺陷，卷筒刚度较大时，内部径向压力与切向应力都比较大，铝带材容易出现扁卷现象，所以需要合理选择卷筒的刚度。

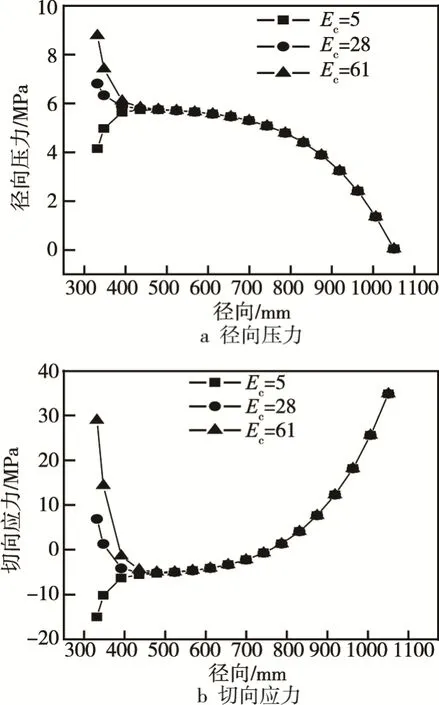
图6 卷筒刚度对铝带卷应力的影响Fig.6 Influences of drum stiffness on stress of aluminum strip

4 结论

1) 冷轧铝带卷取内层径向压力最大，并且随卷径的增大而减小，其中内部区域与外部区域径向压力沿半径方向下降较快，而中部区域变化较为平缓；带卷内部切向应力较大，随后减小，在外层一定区域开始再增大，最外层切向应力与卷取张应力相等。

2) 径向压缩系数的理论值与实验值相符；计算内部应力分布时，需要考虑铝带卷的各向异性以及层与层之间的紧密程度。

3) 卷筒刚度对铝带卷内层应力影响较大，而对外层影响很小，卷筒刚度较小时，在卷芯处容易产生塌卷缺陷，卷筒刚度较大时，容易出现扁卷现象，合理选择卷筒的刚度，有利于铝带材的卷取。

[1] 连家创, 李春满. 轧钢设备及工艺(第一分册钢板轧机)[M]. 哈尔滨: 东北重型机械学院出版社, 1985:134—138.LIAN Jia-chuang, LI Chun-man. Rolling Equipment and Technology (The First Volume Plate Mill)[M]. Harbin:Northeast Heavy Machinery Institute Press, 1985: 134—138.

[2] 周国盈. 带钢精整设备[M]. 北京: 机械工业出版社,1982.ZHOU Guo-ying. Strip Finishing Equipment[M]. Beijing:Machinery Industry Press, 1982.

[3] PARK W W, KIM D K, IM Y T, et al. Effects of Processing Parameters on Elastic Deformation of the Coil During the Thin-strip Coiling Process[J]. Metals & Materials International, 2014, 20(4): 719—726.

[4] 白振华, 司红鑫, 周庆田, 等. 热轧带钢卷取过程中钢卷内部应力模型的研究[J]. 机械工程学报, 2014, 50(2):110—115.BAI Zhen-hua, SI Hong-xin, ZHOU Qing-tian, et al. Research on Steel Roll Internal Stress Model in Hot Rolled Strip Coiling Process[J]. Chinese Journal of Mechanical Engineering, 2014, 50(2): 110—115.

[5] PARK K T, YONG H P, PARK H C, et al. Stress Analysis of Cold Rolled Strip Coiling Process[J]. Transactions of the Korean Society of Mechanical Engineers A, 2017,41(5): 409—414.

[6] SUN W Q, ZHANG X Y, HE A R, et al. Research on Ridge Buckle of High Accuracy Cold Rolled Thin Strip at Local High Points During the Coiling Process[J]. La Metallurgia Italiana, 2016, 108(1): 45—52.

[7] 白振华, 连家创, 吴彬, 等. 冷轧钢卷卷取过程内部应力三维分布的研究[J]. 钢铁, 2001, 36(9): 42—45.BAI Zhen-hua, LIAN Jia-chuang, WU Bin, et al. Research of Three-dimensional Distribution of Internal Stress in Strip Coiling Process[J]. Steel, 2001, 36(9):42—45.

[8] WANG Yong-qin, LI Li, YAN Xing-chun, et al. Modeling of Stress Distribution During Strip Coiling Process[J].Journal of Iron and Steel Research (International), 2012,19(8): 6—11.

[9] HOOG F R D, COZIJNSEN M, YUEN W Y D, et al.Predicting Winding Stresses for Wound Coils of Linear Orthotropic Material[J]. ARCHIVE Proceedings of the Institution of Mechanical Engineers Part C Journal of Mechanical Engineering Science, 2004, 218(1): 27—38.

[10] LIU M L. A Nonlinear Model of Center-wound Rolls Incorporating Refined Boundary Conditions[J]. Computers & Structures, 2009, 87(9/10): 552—563.

[11] 胡小虎. 带钢热连轧地下卷取机卷筒压力的有限元解法[D]. 秦皇岛: 燕山大学, 2001.HU Xiao-hu. Finite Element Solution of Scroll Pressure of Down-coiler for Hot Strip Mill[D]. Qinhuangdao:Yanshan University, 2001.

[12] 李海亮. 冷轧卷取机振动及张力分布的研究[D]. 秦皇岛: 燕山大学, 2008.LI Hai-liang. The Research on Coiling Vibration and Tension Distribution[D]. Qinhuangdao: Yanshan University, 2008.

[13] 常铁柱, 张清东, 丁军. 冷轧带钢卷取过程中受力与变形研究[J]. 钢铁, 2008, 43(4): 51—56.CHANG Tie-zhu, ZHANG Qing-dong, DING Jun. Study on Deformation of Cold-rolled Steel Strip During Coiling[J]. Steel, 2008, 43(4): 51—56.

[14] 连家创. 卷取机卷筒单位压力的计算[J]. 燕山大学学报, 1979, 16(Z1): 4—12.LIAN Jia-chuang. Calculation of Unit Pressure in Drum of Coiler[J]. Journal of Yanshan University, 1979, 16(Z1):4—12.

[15] HAKIEL Z. Nonlinear Model for Wound Roll Stress[J].Tappi Journal, 1987, 70.

[16] Stormy Attaway. MATLAB编程与工程应用[M]. 北京:电子工业出版社, 2013.Stormy Attaway. MATLAB Programming and Engineering Applications[M]. Beijing: Electronics Industry Press,2013.

[17] 丁修堃. 轧制过程自动化[M]. 北京: 冶金工业出版社,2009.DING Xiu-kun. Rolling Process Automation[M]. Beijing:Metallurgical Industry Press, 2009.

Finite Difference Simulation of Internal Stress for Cold Rolled Aluminum Stripcoil

ZHANG Bo1,WANG Wei1,2,LI Shi-miao1
(1. College of Mechanical Engineering and Automation, Fuzhou University, Fuzhou 350100, China;2. Collaborative Innovation Center of High-End Equipment Manufacturing in Fujian, Fuzhou 350100, China)

The paper aims to study distribution of internal stress in coiling of cold rolled aluminum strip and influencing factors to provide reference for design of aluminum strip drum. Through the cold rolling of aluminum compression test, relation curves for radial compression coefficient and stress of aluminum strip were determined; nonlinear finite difference method was used to simulate coiling process and internal stress; effects of linear, first-order nonlinear and second-order nonlinear material models and stiffness of drum on stress distribution inside the roll were analyzed. The calculated radial compressive coefficient was in good agreement with the experimentally values; drum stiffness had great influence on inner stress of aluminum coil, but had little effect on the outer layer. When stiffness of drum was small, it was easy to produce collapse defect at core, when drum stiffness was large, it was easy to flat rolling phenomenon. When calculating internal stress distribution of a coil, it is necessary to consider the anisotropy of the aluminum coil and the tightness between the layers, reasonable choice of rigidity of drum has great practical significance on improving the coil quality.

cold rolled aluminum strip; finite difference method; radial compression coefficient

2017-12-08

国家自然科学基金（51375094）；福建省科技计划（2018H0101）

张波（1993—），男，硕士研究生，主要研究方向为金属材料精密成形工艺及装备设计。

王伟（1970—），男，博士，教授，主要研究方向为现代机械设计理论及方法、冶金设备力学及控制。

10.3969/j.issn.1674-6457.2018.01.016

TG335

A

1674-6457(2018)01-0127-05