深水钢悬链立管J型铺设时域动力分析

，

(1.上海船舶运输科学研究所，上海 200135；2.上海交通大学 船舶与建筑工程学院，上海 200240)

深水钢悬链立管J型铺设时域动力分析

张立1，徐莹2

(1.上海船舶运输科学研究所，上海 200135；2.上海交通大学 船舶与建筑工程学院，上海 200240)

针对深水钢悬链立管的J型铺设作业的时域动力响应特性，先利用悬链线理论对其进行静力分析，基于动力控制方程，以集中质量法求解得到系统刚度矩阵，考虑船体运动、波流载荷以及管土作用，根据广义α理论将时间离散后积分求解，建立数值求解迭代步骤，得到立管受力分析结果。以3 000 m水深钢悬链立管J型铺设为例，使用OrcaFlex软件进行计算分析，结果表明：①触地点的冯米塞斯应力和弯曲应力最大，立管顶端的有效张力最大；②铺管船的性能影响立管铺设，对触地点冯米塞斯应力和弯曲应力以及顶端有效张力的时域分析表明，其幅值变化范围较窄，铺设系统稳定；③校核API规范，各项数据满足铺设要求，可以为工程实际提供参考。

钢悬链立管；J型铺设；时域分析；集中质量法；动力分析

钢悬链立管(steel catenary riser,SCR)最大特点是集海底管道和生产立管功能于一身，又以其良好的适用性以及低廉的价格成为立管系统的首选形式[1]。SCR的铺设是立管投入使用的第一步，J型铺设，以立管近乎垂直下放到水中的形态而得名，能够使钢悬链立管产生更小的应力，成为深水立管铺设中的最优选择[2]。J型铺设过程中，钢悬链立管运动具有强非线性，为满足精度要求，需采用时域分析求解。与有限元方法、有限差分法，以及摄动法等相比，集中质量法能够避免大系统耦合方程的出现，具有较强的优越性。王安姣等[3]基于集中质量法求解了柔性立管的非线性动力分析，并使用Newmark方法数值求解；Chai等[4]建立了钢悬链立管的三维集中质量法求解方程，但是仅适用于平动自由度；J.E.Gutierrez等应用集中质量法，对锚泊系统与平台进行完全耦合分析，证明了集中质量法的可靠性；何宁等[5]用Abaqus建立了钢悬链立管的有限元三维动力分析模型，认为钢悬链立管动力响应的非线性特征，并且其结果证明悬挂点和触地点附近的应力较高；李艳等[6]利用集中质量法对钢悬链立管、柔性立管进行非线性动力分析，并使用Newmark-β法求解，同时对于立管顶端受力进行时域分析。以上研究中对立管的计算没有计入船体的影响，并且Newmark-β法在时域计算过程中存在着步骤不够简洁、收敛性不够好的问题。为此，考虑利用悬链线理论进行静力分析，在此基础上基于集中质量法进行动力分析，计入船体运动、波流载荷和管土作用，使用广义α法将时间离散后积分求解，建立数值求解迭代步骤，使用OrcaFlex软件对铺管船-钢悬链立管系统进行时域动力分析，根据API规范校核钢悬链立管动力分析过程中的最大von Mises应力，最大弯曲应力、有效张力以及倾斜角。

1 理论分析

1.1 静力分析

SCR的静力分析是动力分析的基础，为动力分析提供初始平衡位置。作为动力分析的初步计算理论，悬链线理论是近几年来常用的静力分析方法，高效而且简单。J型铺设见图1。

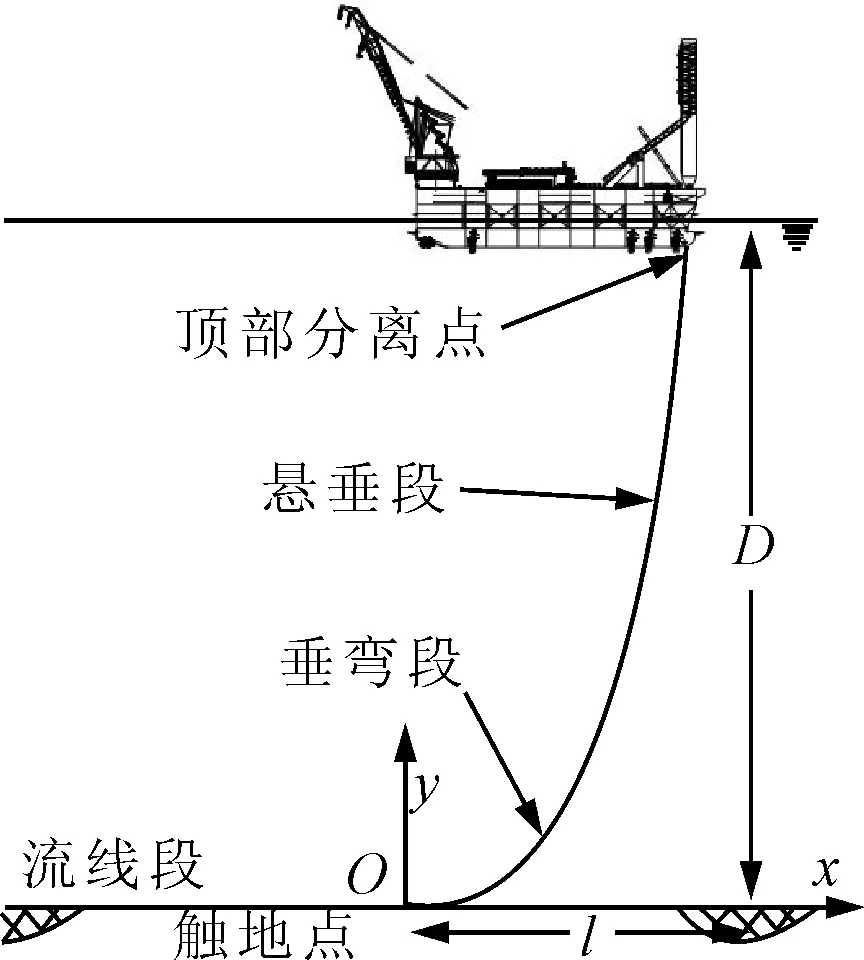
图1 J型铺设示意

悬链线的控制方程为

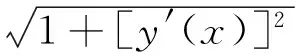
(1)

式中:δ=w/H，w为湿重，H为立管水平方向的恒定力。触地点处的边界条件如方程(2)所示，其中Θ0为海床坡角。

(2)

1.2 动力分析

钢悬链式立管遭受风浪流载荷，其动力响应相对复杂。在得到立管静力分析结果之后，动力分析是立管分析的重要方面。钢悬链立管的运动包含着强非线性，常用时域分析方法主要有细长杆理论和集中质量法2类。细长杆理论在原理上较为严谨，但计算过程相对复杂；集中质量法对问题进行简化，易于实现，计算高效，经过较长时间的发展，已经广泛用于立管和锚泊系统动力分析[7]。

集中质量法将管线离散成一系列无质量的直弹簧和质量节点，动力分析控制方程[8]为

(3)

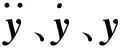
图2 单元间夹角变化示意[9]

根据应变能理论，单元m拉伸应变能Vm为

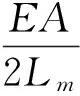
(4)

式中：EA为轴向刚度；Lm为单元m的原长。对应轴向刚度矩阵的矩阵项可以表示为方程(5)或(6)：

(j≠i)

(5)

(6)

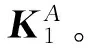
(7)

而弯曲应变能表示为

(8)

(9)

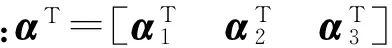
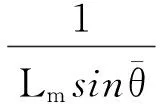
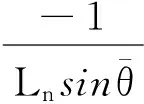
α2=-α1-α3

(10)

由此得到的弯曲刚度矩阵：

(11)

根据方程(7)和(11)组装轴向刚度矩阵和弯曲刚度矩阵，得到方程(3)的刚度矩阵K，然后利用数值计算得到相应参数。

1.3 运动响应计算

立管运动响应主要表现为3部分：上部船体运动的影响、环境载荷的影响以及管土耦合作用。

1)上部船体运动的影响。立管重量相对于船体为小量，因而船体对立管的运动采取非耦合计算，使用AQWA水动力分析软件计算得到运动幅值响应，以此作为时域分析时立管上部运动的边界条件。

2)环境载荷的影响。作用于立管的环境载荷主要是波浪力和海流作用力，波浪力使用经验Morison方程计算，而海流作用力则分为横向拖曳力和顺流向的升力计算。

3)管土耦合作用。管土耦合是立管分析中不可忽略的因素，在J型铺设过程中，立管与海床的接触时间有限，因而管土耦合的非线性作用并不明显。为简化计算，本文使用线性土壤模型，认为土壤刚度为线性，并且忽略土壤的剪切力，仅计入SCR流线段的法向力。土壤对立管的法向力按照式(12)计算。

FN=KNAd

(12)

式中：KN为土壤的法向刚度；A为立管在土壤中的渗透面积；d为立管陷入土壤的深度。

1.4 时域动力分析数值求解

当静力分析结果满足要求，在得到静力分析结果之后，得到立管每一个节点的位置、转角，以及受力和弯矩等，将其结果作为动力分析的起始计算位置；使用集中质量法，设置时间步长dt和收敛条件ε，进行时域分析。方程(3)是非线性方程，需对时间进行离散，然后通过数值方法进行积分求解，本文计算基于广义α理论[10]。

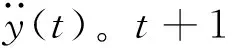
(13)

(14)

基于方程(13)和(14)得到t+1时刻的y(t+1)，当满足收敛条件|y(t+1)-y(t)|/y(t)<ε，即可迭代计算t+2时刻。

1.5 动力分析计算步骤

静力分析结果给出了动力分析的计算初值，当得到t时刻的加速度、速度和位移等参数之后，根据广义α理论获得t+1时刻即t+dt的参数，据此计算是否满足收敛条件，若满足收敛条件计算下一时刻结果，直到时间终止。最后，输出所需结果。计算流程见图3。

图3 动力分析计算步骤

1.6 管道应力计算

在得到立管的各个力学参数之后，计算立管的von Mises应力矩阵如方程(15)所示。

(15)

式中：σZZ为由于轴向力和弯矩导致的轴向应力；σCC和σRR为基于兰姆厚壁理论得到的环向和径向应力；τRC，τRZ以及τCZ为剪应力项。

2 模型建立

基于上述计算理论，使用OrcaFlex软件计算钢悬链立管的3 000 m水深J型铺设，对立管进行时域动力分析。设置模型参数如下。

2.1 铺管船数据以及环境参数

船长225 m，型深45 m，型宽90 m，吃水为27 m，排水量264 585 t，铺管船的起重能力为900 t，J型塔位于船首位置。环境参数见表1，时间步长为0.01 s，收敛条件ε为25×10-6，动态分析时间为300 s。

表1 J型铺设环境参数

2.2 立管数据

立管总长4 000 m，流线段700 m，杨氏模量212 GPa，泊松比0.3，材料密度为7 850 kg/m3，钢材等级为X65钢，立管表面涂层GSPU保温材料，立管截面视图见图4。海床对立管的作用设置为线性刚度土壤，数据见表2。

图4 钢悬链立管截面示意

项目数值项目数值外径/m0.2731附加质量系数1壁厚/m0.0254阻力系数1.6涂层厚度/m0.0508升力系数0.9许用应力系数0.8土壤刚度/[(kN/m)·m-2]100

3 结果分析

基于悬链线理论和集中质量法的钢悬链立管J型铺设时域动力分析结果见图5～图8，最小值、最大值和平均值分别表示分析过程中管长节点的最小值、最大值和平均值，计算结束后，收集三者的数值，并作图。

图5 最大冯米塞斯应力

最大von Mises应力从顶端开始沿着管长方向逐渐增大，在触地点位置达到最大，在海床流线段部分的应力基本不变，主要成分是轴向应力。因而在设计分析时，需要着重加强触地点位置的保护，防止触地点位置出现因应力过大所导致的破坏。

图6 最大弯曲应力

最大弯曲应力在触地点位置最大，垂弯段弯曲应力相对较大，而悬垂段和流线段部分由于曲率较小，弯曲应力近似为0。

图7 有效张力

铺管船的张紧系统为SCR提供张力，SCR的有效张力从顶端沿着管长方向逐渐降低，流线段部分有效张力的变化趋势变缓，管线的轴向力成分减少，主要是水平恒力。

图8 倾斜角

倾斜角是立管与竖直向上方向的夹角，如图8所示。顶端最大，意味着SCR的悬挂角度最小，悬挂角为5.95°；倾斜角最小为90°表示SCR与海床接触，处于水平拉伸状态。

计算结果见表3。

表3 时域动力分析计算结果

表3中表示了最大值位置的时域分析结果，见图9～图11。图9、图10和图11描述触地点(3 203 m)处的应力和张力时域分析，其幅值在一个较窄范围变化，表明J型铺设系统相对稳定。

图9 触地点冯米塞斯应力时域分析结果

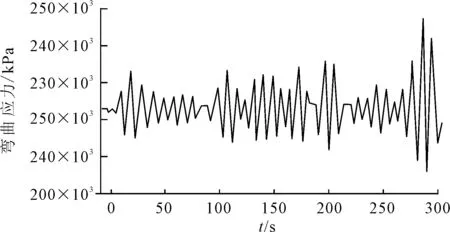
图10 触地点弯曲应力时域分析结果

图11 立管顶端有效张力时域分析结果

根据以上计算，得到以下结果。

1)J型铺设的悬挂角为2.9°。

2)触地点的冯米塞斯应力、弯曲应力和立管顶端有效张力的时域分析结果表明其幅值变化范围较小，J型铺设系统稳定。

3)校核API RP 2RD规范，SCR的许用应力为358 540 kPa，铺管船的满载铺管能力为900 t，表3数据表明满足铺设要求。

4 结论

1)钢悬链立管随铺管船运动的非线性特征明显，立管触地点位置的变形大，产生的冯米塞斯应力最大；铺管船的张紧系统为立管提供张力，立管顶端产生的有效张力最大，海底流线段主要承受水平力。

2)铺管船的稳定性影响着立管应力的变化范围，因此在设计船型时，应当着重考虑船舶的抗风浪能力；同时铺设立管时候也应选择温和的环境，避免恶劣环境。

[1] 宋儒鑫.深水开发中的海底管道和海洋立管[J].船舶工业技术经济信息,2003(6):31-42.

[2] LENCI S, CALLEGARI M. Simple analytical models for the J-lay problem[J]. Acta Mechanica,2005(1/2):23-39.

[3] 王安姣,陈加菁.柔性立管的非线性动力分析[J].海洋工程,1991(3):12-22.

[4] CHAI Y, VARYANI K, BARLTROP N. Three-dimensional Lump-Mass formulation of a catenary riser with bending, torsion and irregular seabed interaction effect[J]. Ocean Engineering,2002,29(12):1503-25.

[5] 何宁,王波,王辉,等.深水钢悬链线立管三维动力分析[J].中国海上油气,2010(2):129-133.

[6] 李艳,李欣.深水钢悬链线立管非线性动力分析[J].船舶工程,2013(6):106-111.

[7] 陈海飞.深水柔性立管非线性静动力分析[D].青岛:中国海洋大学,2011.

[8] 缪国平.挠性部件力学导论[M].上海:上海交通大学出版社,1995.

[9] 宋环峰.深水S型管线铺设数值分析及优化控制[D].哈尔滨:哈尔滨工程大学,2013.

[10] CHUNG J, HULBERT G M. Time integration algorithm for structural dynamics with improved numerical dissipation: the generalized-method[J]. Journal of Applied Mechanics, Transactions ASME,1993,60(2):371-375.

Time Domain Dynamic Analysis of Steel Catenary Riser in J Lay Operation

ZHANGLi1,XUYing2

(1.Shanghai Ship and Shipping Research Institute, Shanghai 200135, China; 2.School of Naval Architecture, Ocean and Civil Engineering, Shanghai Jiaotong University, Shanghai 200241, China)

The dynamic responses of steel catenary riser in J-lay operation were analyzed in time domain. The catenary theory was used for static analysis. Stiffness matrix was obtained based on lumped mass method. The motion of vessel, wave and current load, and the riser-soil interaction were considered. According to the Generalised-αintegration scheme, the simulation time was discreted to setup the numerical solution iteration steps. The dynamic response of the steel catenary riser in J-lay operation in 3 000 m water depth was analyzed. The results showed that the max von Mises stress and bending stress occur at touch down point (TDP); the max effective tension is at the top end of the riser; the J-lay system is stable, because the amplitude variation range of the von Mises stress and bending stress at TDP and the effective tension at the top end are narrow. After checking API code, all the results meet the operation requirements.

steel catenary riser (SCR); J lay; time domain analysis; lumped mass method; dynamic analysis

P754;TE973.1

A

1671-7953(2017)06-0122-05

10.3963/j.issn.1671-7953.2017.06.028

2017-03-13

2017-04-05

国家科技重大专项(2011ZX05027-002-004-008)

张立(1991—)，男，硕士，工程师

研究方向：立管与涡激振动，船模水池实验