基于敏感度的灰色关联及AHP修正方法

魏文强，李岩松

（淮安市水利勘测设计研究院有限公司 南京分公司，南京211100）

基于敏感度的灰色关联及AHP修正方法

魏文强，李岩松

（淮安市水利勘测设计研究院有限公司 南京分公司，南京211100）

以某边坡为实例，分别进行了灰色关联法与层次分析法修正的灰色关联法的敏感度计算，对比可以发现，层次分析法修正的灰色关联模型中，土体的内摩擦角与粘聚力对安全系数的影响排序结果与未修正结果相同，但坡高、容重与坡率的排序发生了变化，经分析，认为修正的结果更具有参考性。

边坡；稳定性；灰色关联法；层次分析法；安全系数；敏感度

在边坡工程中，有较多的因素对边坡的稳定性会造成影响［1］，诸如黏聚力、内摩擦角、容重、边坡角、边坡高度等［2-3］，但有些因素影响较大，有些因素影响较小，各个影响因素对边坡稳定性所造成的影响及其贡献程度不同［4-5］，因此，有必要对边坡影响因素的敏感性进行分析，基于敏感性的分析，可以找出影响边坡稳定特性的主要因素，进而可以有针对性地施加相关措施。

灰色关联分析可以得出比较因素与参考因素之间的关联程度［6］，适用于敏感度分析，其所得的关联度越大，说明要比较因素对上层参考因素变化的相关性越强，属于敏感性分析范畴，因此，可将关联度大小作为评判敏感性的依据，对于边坡，其稳定性的主要表征参数为安全系数，因此，该文将从安全系数出发分析其影响因素的敏感性，同时，在采用灰色关联法的基础上，还提出了一种层次分析法修正的灰色关联法，以供相关工程人员进行参考。

1 灰色关联分析法的基本原理和方法

1.1 确定参考序列和比较序列

对于边坡稳定性的敏感性分析，实质上就是探究各个影响边坡稳定性的因素对边坡安全系数的影响程度，影响边坡稳定性的影响因素较多，该文重点分析黏聚力、内摩擦角、容重、边坡角、边坡高度对边坡稳定性的影响，因此选取Xi=［xi（1），xi（2），…，xi（n）］作为比较序列的描述，i数值的不同分别代表黏聚力、内摩擦角、容重、边坡角、边坡高度，内标数字的不同代表影响因素的取值不同，其可表示为矩阵X，如式（1）。

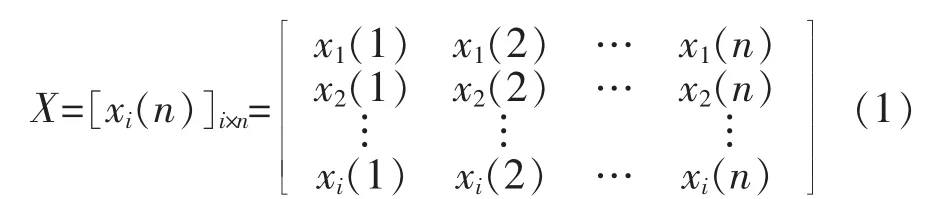
同理，选取为比较序将边坡的安全系数作为参考序列Y，Yi=［yi（1），yi（2），…，yi（n）］代表比较序列对应参数下计算所得的安全系数值，其矩阵形式如式（2）。

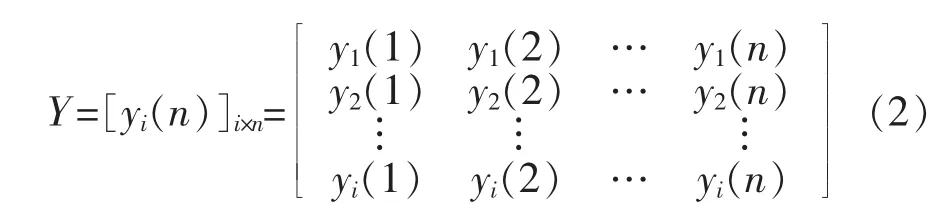
1.2 数据序列无量纲化

黏聚力、内摩擦角、容重、边坡角、边坡高度因其量纲单位的不同，会造成数值大小的较大悬殊，若以此进行敏感性影响比较，将会有较大误差。因此，必须运用特定的方法进行影响因素的无量纲化，无量纲化后的数据方可进行直接比较。

无量纲的转化方法有初值化、归一化、区间相对值化和均值化方法，该文采用区间相对值化方法，如式（3）～式（4）。

1.3 灰色关联系数

灰色关联系数表征黏聚力、内摩擦角、容重、边坡角、边坡高度与边坡安全系数的紧密关联程度，其值大于0小于1。 关联系数γ0i（k）可由式（5）求出：

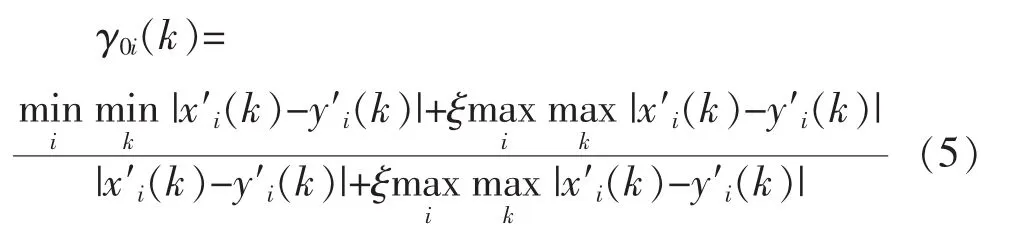
其中，ξ∈［0，1］，称为分辨系数，一般将其值取为0.5。

1.4 灰色关联度

比较序列（黏聚力、内摩擦角、容重、边坡角、边坡高度）与参考序列（安全系数）在各指标处的关联系数的平均值即为两序列的关联度：

式中 γ0i∈（0，1］，γ0i越大，表明边坡稳定性的影响因素对边坡安全系数影响越大，若γi＞γj，j=1，2，…，n，说明因素Xi对边坡安全系数的敏感程度高于因素Xj。

2 灰色关联法的AHP修正

灰色关联法考虑的是各个边坡稳定性的影响因素对安全系数的关联程度，其通过计算，可得到一个关联度矩阵γi=［γ1，γ2，…，n］，以这种关联度矩阵表征黏聚力、内摩擦角、容重、边坡角、边坡高度对安全系数的敏感度。但灰色关联法所得的敏感度表征的是单个因素对安全系数的敏感程度的影响，且是一种定量的理论比较，而没有进行各个因素之间的横向比较，同时也没有经具有相关专业实践经验的专家进行比较，因此，其所得敏感度值具有参考性，但参考价值一般。

而层次分析法（AHP）可以弥补上述缺陷，即其进行了各个因素之间的横向比较，并请具有相关专业实践经验的专家进行打分，因此，在考虑该因素的敏感性时，应将二者进行有机结合。该文便将灰色关联法与层次分析法进行结合。

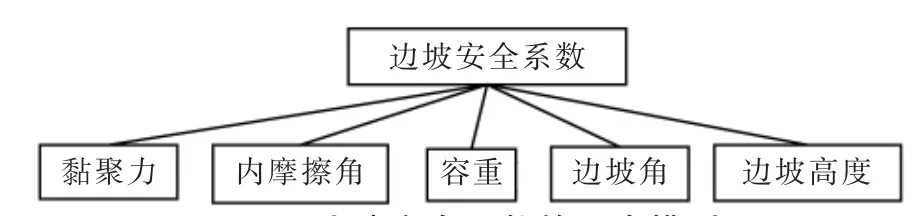
图1 边坡安全系数的层次模型

采用层次分析法对图1层次模型进行分析，层次分析法由因数集和评价集组成。层次分析法AHP基于式（7）～式（8）进行：

对于二级模型，最终得到的权重结果为B=［b1，b2，…，bn］，其中b为权重值。

以层次分析法所得的B矩阵对γi矩阵进行修正，文中采用矩阵各元素相乘的方式进行修正，即γi值与bi值所对应的各个元素相乘的方式进行修正，di=［γ1b1，γ2b2，…，γnbn］结果记为di，即为最终的总体敏感度，di=［γ1b1，γ2b2，…，γnbn］如式（9）。

式（9）敏感度不仅考虑了各个因素之间的横向比较关系，还考虑了具有行业经验实践人员的定性打分情况，同时还考虑了灰色关联法的定量关联分析理论，以此，便完成了层次分析法对灰色关联方法的修正，以其进行敏感度分析，具有一定意义。

3 实例边坡敏感性分析

某一边坡［7］场地为山麓斜坡地形地貌，是一水稻种植田，其在未开挖前的地形地貌为阶梯形状，走向为自西向东，并呈倾斜状，该处边坡于2003开挖，开挖后，形成100m宽，8～15m高，坡角10°～15°，坡向75°的边坡，由于在开挖时，产生了较大的位移变形，在该边坡的东南角位置出现了小规模滑坡。

残积砂质黏性土是该边坡临空面地层主要土性材料，该文的敏感性分析只针对该地层进行，根据该地层的资料显示，可以得到相关敏感性分析的重要参数：土体容重V=16.7kN/m3，黏聚力c=10kPa，内摩擦角φ=20°，坡高h=10m，坡率m=1∶1，因此，对于该例的敏感性分析，将从土体容重、黏聚力、内摩擦角、坡高与坡率（边坡角）方面去分析。

采用Bishop法对边坡稳定性参数进行计算，边坡的安全系数F随各参数的计算结果，如表1～表5。

表1 安全系数随坡高的变化

表2 安全系数随坡率的变化

表3 安全系数随容重的变化值

表4 安全系数随黏聚力的变化值

表5 安全系数随内摩擦角的变化

以土体容重、黏聚力、内摩擦角、坡高与坡率为比较矩阵，即表1～表5所对应的第一行数据；以相对应的安全系数为参考矩阵，即表1～表5所对应的第二行数据，以此便可建立参考矩阵和比较矩阵，如式（10）～式（11）。

对X和Y矩阵采用区间相对值发进行去量纲化，以此差异序列矩阵可以被求得，关联矩阵由此导出，如式（12）。

由上述关联矩阵，便可求出各个影响因素对安全系数的关联度，如式（13）。

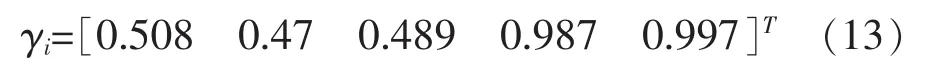
根据式（12），所得的关联度顺序为：土体内摩擦角＞黏聚力＞坡高＞容重＞坡率（坡角）。

采用层次分析法，对上述关联度进行修正，层次分析法具体的计算与打分过程由于篇幅所限，在此，就不做阐述，层次分析法对土体容重、黏聚力、内摩擦角、坡高与坡率五因素所得的权重结果为：

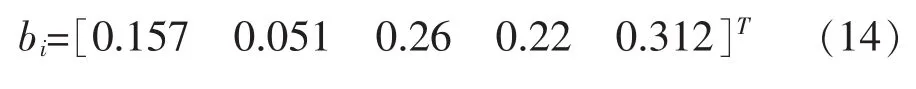
根据式（9），将式（13）各元素与式（14）各元素相乘，便可得到文中所述的灵敏度值：

式（15）的结果显示，各因素对安全系数的灵敏度为：土体内摩擦角＞黏聚力＞容重＞坡率（坡角）＞坡高。与式（12）所得结果进行对比可以发现，层次分析法修正的灰色关联模型中，土体的内摩擦角与黏聚力对安全系数的影响排序结果与未修正结果相同，但坡高、容重与坡率的排序发生了变化；另外，修正后的模型更加突出了黏聚力与内摩擦角对安全系数影响的敏感程度，而弱化了容重与坡率对安全系数影响的敏感度。

根据层次分析法修正的灰色关联模型，总体结果表明，内摩擦角与黏聚力对安全系数的影响较为敏感，容重对安全系数的影响也较大，而坡率与坡高对安全系数的影响表现为钝性，影响程度较小。

层次分析法修正的灰色关联模型，在吸纳了灰色关联法的优点外，还进行了各个因素之间的横向比较，且具有相关专业实践经验的专家进行打分，鉴于此，认为层次分析法所修正的敏感度结果更为可靠。

4 结语

（1）通过层次分析法对传统灰色关联方法进行了修正，可以弥补缺陷，即其进行了各个因素之间的横向比较，并请具有相关专业实践经验的专家进行打分，因此，在考虑该因素的敏感性时，应将二者进行有机结合。

（2）以某边坡为实例，分别进行了灰色关联法与层次分析法修正的灰色关联法的敏感度计算，对比发现，层次分析法修正的灰色关联模型中，土体的内摩擦角与黏聚力对安全系数的影响排序结果与未修正结果相同，但坡高、容重与坡率的排序发生了变化；另外，修正后的模型更加突出了黏聚力与内摩擦角对安全系数影响的敏感程度，而弱化了容重与坡率对安全系数影响的敏感度，认为修正结果更具参考性。

［1］潘盛泽，罗平，高奋飞.库水位变化对全强风化边坡稳定性的影响［J］.甘肃水利水电技术，2017，53（1）：28-32.

［2］麦麦提明·依比布拉.基于瑞典法和毕肖普法对比的边坡稳定性［J］.水利科技与经济，2015，21（6）：12-14.

［3］李志刚，汤博.基于MATLAB下BP神经网络的边坡稳定性预测［J］.水科学与工程技术，2013（5）：25-28.

［4］王英豪.利用赤平极射投影法评价岩质边坡稳定性［J］.水科学与工程技术，2011（6）：57-59.

［5］李幸周，许丽，王延洪.基于MATLAB边坡稳定性分析的土坝断面优化［J］.陕西水利，2009（3）：119-120.

［6］孙玉刚.灰色关联分析及其应用的研究［D］.南京：南京航空航天大学，2007.

［7］陈志波，简文彬.边坡稳定性影响因素敏感性灰色关联分析［J］.防灾减灾工程学报，2006，26（4）：473-477.

Grey relational analysis and AHP correction method for sensitivity of slope stability characteristics

WEI Wen-qiang，LI Yan-song
（Huaian Water Conservancy Survey&Design Institute Co.， Ltd.， Nanjing 211100， China）

A slope for example， the sensitivity was computed by Grey-correlation degree analysis method and AHP modified Grey-correlation degree method， respectively.AHP Grey-correlation degree relational model correction method，the soil friction angle and cohesion influence on the safety factor of the results were the same sort of correction results，but the slope high that changed，the bulk density and slope rate of sorting by analysis that correction results of more reference.

slope； stability； grey relational analysis； analytic hierarchy process； safety coefficient； sensitivity

TD824.7 文献标识码：B 文章编号：1672-9900（2017）05-0082-04

2017-05-22

魏文强（1986-），男（汉族），陕西宝鸡人，工程师，主要从事水利水电工程规划及设计工作，（Tel）17355253212。

王艳肖）