基于数据同化技术的地质参数反演分析研究

秦耀军，周晓勇，杨亚宾，贾 超

（1.山东省地质矿产勘查开发局第二水文地质工程地质大队，山东 德州 253072；2.山东大学 土建与水利学院，济南250061）

工程勘察

基于数据同化技术的地质参数反演分析研究

秦耀军1，周晓勇2，杨亚宾1，贾 超2

（1.山东省地质矿产勘查开发局第二水文地质工程地质大队，山东 德州 253072；2.山东大学 土建与水利学院，济南250061）

通过数据同化技术用卡尔曼滤波算法对观测井所得水位监测资料进行同化计算，在得到较为精确水位观测值的基础上对主要取水层的渗透系数进行参数反演，并与前期室内试验获得的渗透系数对比，表明通过数据同化过滤之后进行的参数反演更精确有效。

数据同化；卡尔曼滤波；渗透系数；参数反演

1 研究背景

近年来随着计算机技术的快速发展，用数值分析方法研究地下水运动规律已发展成为地下水研究领域中的重要手段之一，特别是在对复杂的地下水问题进行分析时，数值分析方法能节省大量的人力物力。但为使刻画的模型能够符合真实情况，使计算过程加快收敛、缩减计算量，计算结果更加可靠，则需要提供精确的模型参数［1-3］。

含水层的地质构造虽然是确定的，但含水层的性质在空间和时间上往往表现出极大的差异性，地下水流动发生的环境一般又比较复杂，通过稀少的钻孔资料很难对含水层特征进行准确的描述，所以根据掌握的观测资料利用反演分析的方法反演出含水层的特征对研究地下水流动十分必要。

由于观测技术发展，易获得很多原位观测资料，但这些观测资料都带有一定误差，而且多不连续，所以用这些直接观测的数据对含水层性质进行描述也不精确，如何有效利用这些误差较大的观测数据，从中得到更有价值的信息，来降低数值模拟的不确定性，使之可以用于地下水的计算和预测，是一个十分重要的研究课题。目前常用数据同化技术来调和多来源的观测信息，并对观测数据进行修正，最后从中得到较为准确的信息，满足正确刻画地下水含水系统的要求。在数据同化方法中卡尔曼滤波法是应用较广，研究比较成熟的一种方法，最早由美国学者在20世纪70年代提出并用于军事领域，经过40多年的发展，已广泛应用在大气、海洋、石油等多个领域［4-5］。

2006年，陈燕、张东晓等［6］首次运用集合卡尔曼滤波（EnKF）同化地下水水头及渗透系数的观测资料，对模型的渗透系数场进行了估计，这是集合卡尔曼滤波第一次在地下水领域中得到应用。2008年，Liu和Chen［7］根据实验场的地下水流场，运用该技术同化水文地质观测资料，对地下水模型参数做出了良好的估计。2009年，Huang［8］运用EnKF改善了地下水污染物运移的预测结果，说明了EnKF相比传统方法的优势。2010年，南通超、吴吉春等［9-13］通过局域化函数对小集合估计的协方差进行修正降低了取样噪声对协方差估计的干扰，提高了滤波精度，并将其运用到理想的二维承压水模型中，得到很好的效果。2013年，史良胜等［13-15］将集合卡尔曼滤波方法拓展至补给条件下潜水流动的数据同化问题中，并通过同化水位、水力传导度和降雨补给等测量数据来更新模型状态、反演模型参数，得出在有长期水位动态测量数据时，可通过水位观测值有效地反演出水力传导度和降雨入渗补给系数的结论。2015年，林琳、史良胜等［16］指出用确定性集合卡尔曼滤波方法能够有效减小大尺度问题的抽样误差，通过算例表明该法能够缓解在小样本条件下的系统方差快速衰减，并探讨了该方法在非均质介质和大尺度问题中的应用效果。通过近些年的发展集合卡尔曼滤波在地下水参数反演方面能够获取较好的结果，因此在地下水流场研究中被广泛应用。

2 数据同化技术的基本原理

卡尔曼滤波理论是1960被美国学者Kalman［6］和Bucy提出，对具有高斯误差统计特性数据进行最优顺序同化的一种方法。从包含误差的数据资料里对所求变量，利用最小二乘估计、最小方差估计等方法进行最佳估计，其实质是由量测值重构系统的状态向量，以“预测—实测—修正”顺序进行递推，得到关于状态量的最优估计。首先根据参考场和观测值的特征误差分布，对随机场和得到的观测值进行一定扰动，并利用带有扰动的随机场和观测值进行同化分析计算，得到同化值，然后用这一组估计值的差异作为统计样本进行误差协方差的估计。对这组估计值经过预报后，又得到一组预报值，再将这组预报值重新作为下步同化的随机场继续进行计算。集合卡尔曼滤波与卡尔曼滤波非常相似，其最大不同在于前者应用了集合的思想，其误差协方差矩阵是通过统计方式进行计算，不需要时间上的递推，而卡尔曼滤波算法中计算误差协方差矩阵需要显式计算并在时间步上进行递推。

地下水流动是一个动态变化的过程，在不同的时间有不同的观测资料（如水头值）加入。当有带有误差的观测资料加入时，卡尔曼滤波就可以将观测资料的有用信息吸收到同化系统中去，连续获得时间顺序上的最优估计值，并且不需要重新考虑前面己经处理过的数据，所以地下水渗流用卡尔曼滤波进行同化处理，通过不断优化观测资料，对同化系统进行实时修改，从而获得含有更小误差的估计值。

卡尔曼滤波算法主要包括预测和更新两步，其主要计算步骤由式（1）～式（4）给出。

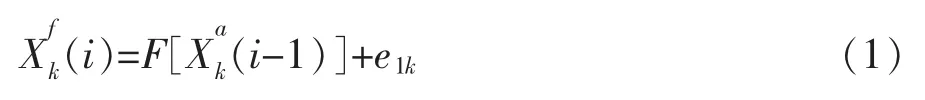
式（1）为EnKF的预报计算过程，X为状态向量，F为预报算子，e为误差，该式表示第i-1到第i时间步长上的预报过程。将前一步同化值作为下一步的初值处理得到预报值。

式（2）为观测向量的递推过程，H为观测算子，d为观测向量，加入随机误差e后则与理论值相吻合。

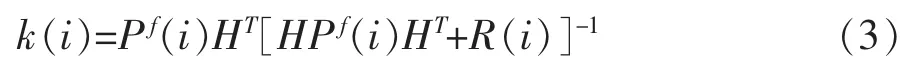
式（3）为卡尔曼增益系数矩阵k的递推过程，P为状态误差协方差向量，R为观测误差协方差向量。

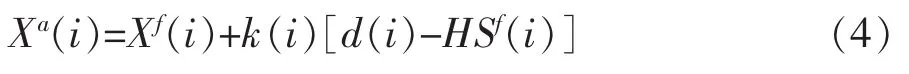
3 工程算例分析

3.1 工程概况

研究区地层属于鲁西北冲洪积平原、冲海积平原区，根据该区域含水层介质的岩性特征，本区域的水存在于第四系和松散沉积岩类的裂隙孔隙中。受影响的因素较多，地质构造、地形地貌、地层岩性及气象水文等都会对地下水的运动造成一定影响。根据现有勘测资料，可划分为5个水文地质亚区，地质环境具有从山前到平原再到滨海的变化特点，含水岩组由全淡水的单层水质结构区逐步过渡到表层淡水～咸水～淡水的3层水质结构区乃至到滨海的全咸水区特点。

本文根据研究内容以德州市市区为计算范围，依据前期搜集的资料分析可知该区取水层主要集中在300～500m的第3含水层到第5含水层，为此本文选取该取水段为研究对象对此段地层的参数进行反演分析研究。

3.2 观测资料的数据同化分析

本节基于卡尔曼滤波在地下水数据同化计算中的应用，借助卡尔曼滤波计算程序对观测孔水头观测值进行同化计算，以获得较为精确的水头值，然后通过地下水流场分析软件MODFLOW进行参数反演。

根据最近德城区地下水开采资料显示，德城区深层地下水的主要开采层位为300～500m含水层，开采井的数量为170眼，占开采井总数的65%，实际开采总量2231.2万m3/a，允许开采资源量1750万m3/a，开采程度123%，属于强超采，根据统计资料把调查所得开采井放到模型中，根据获得的观测资料对每一口取水井水头观测值用卡尔曼滤波进行过滤，部分水头过滤结果如图1～图3。

图1 ZK15观测井水头同化过程

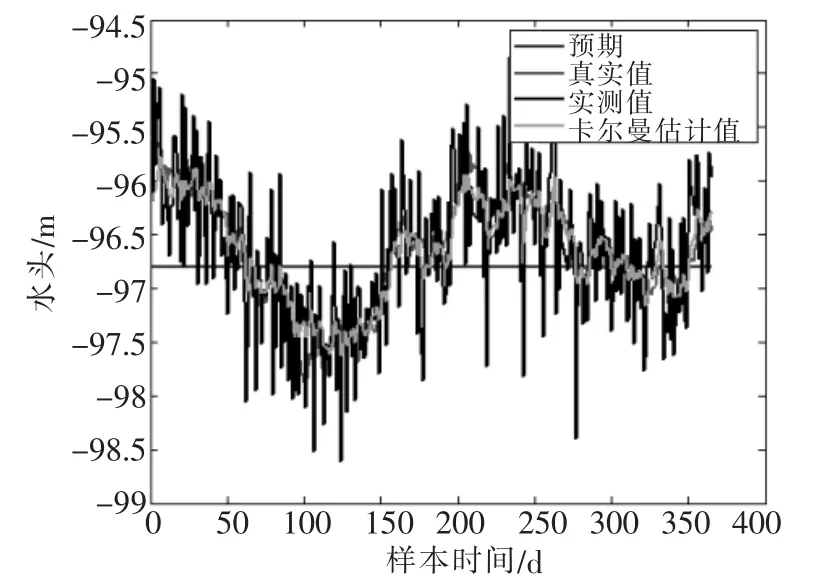
图2 ZK20观测井水头同化过程

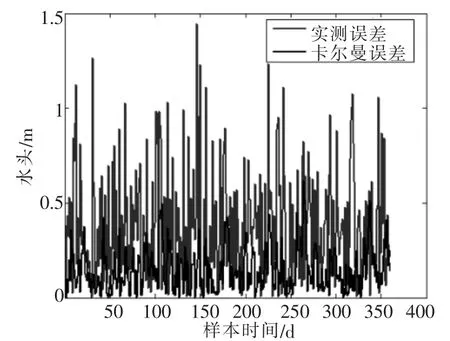
图3 误差分析过程

3.3 研究区渗透系数反演分析

根据研究内容以德州市市区为计算范围，依据前期搜集的资料分析可知该区取水层主要集中在300～500m的第3含水到第5含水层，为此选取该取水段为研究对象建立模型并进行网格剖分如图4。

图4 研究区地下水分析数值模型及网格

共获得83454个单元250362个节点，然后在建立模型的基础上对研究区的地质参数本文主要对渗透系数进行反演。把各个观测井过滤后的水位观测值代入到反演分析软件中，然后对研究的主要取水层的参渗透系数进行反演，第3含水层到第5含水层渗透系数反演结果如图5～图10。

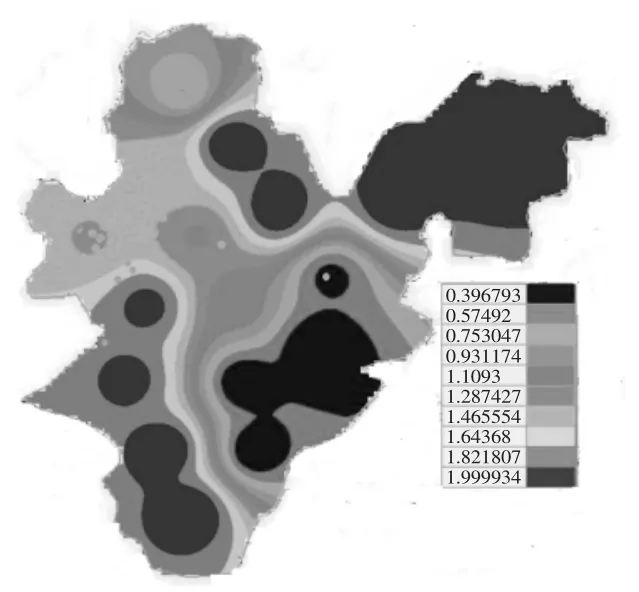
图5 研究区第3含水层渗透性系数分布

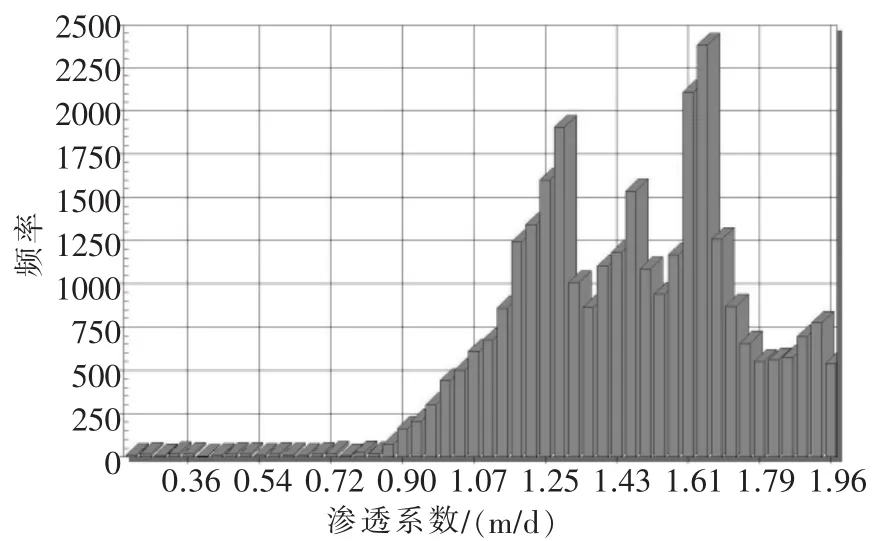
图6 研究区第3含水层渗透系数大小频率

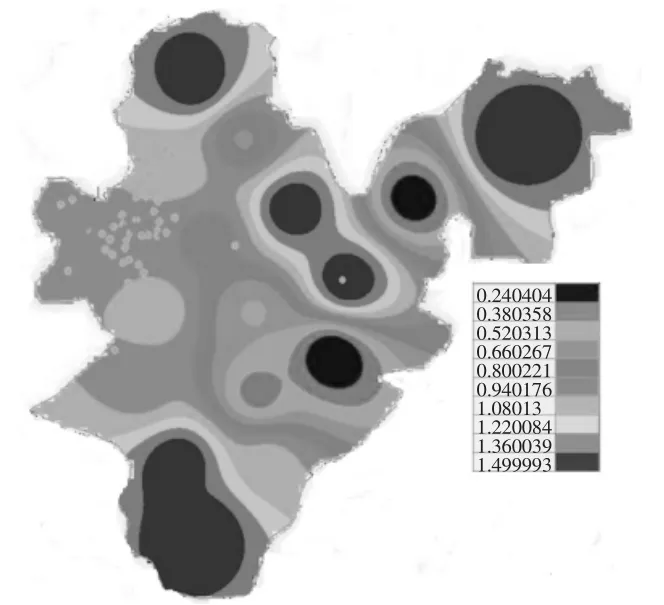
图7 研究区第4含水层渗透系数分布

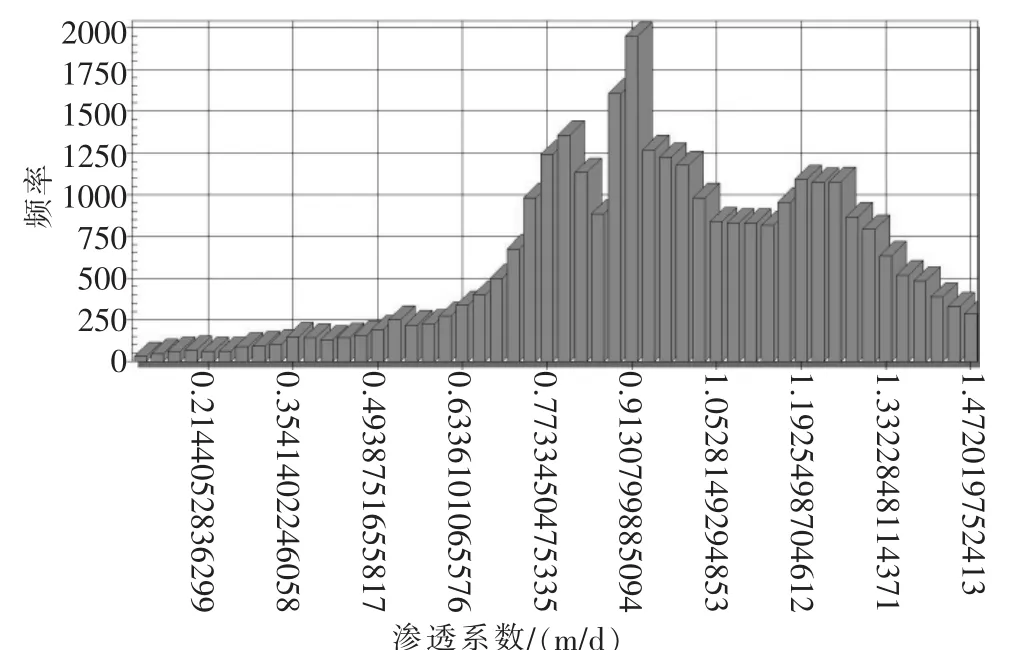
图8 研究区第4含水层渗透系数大小频率

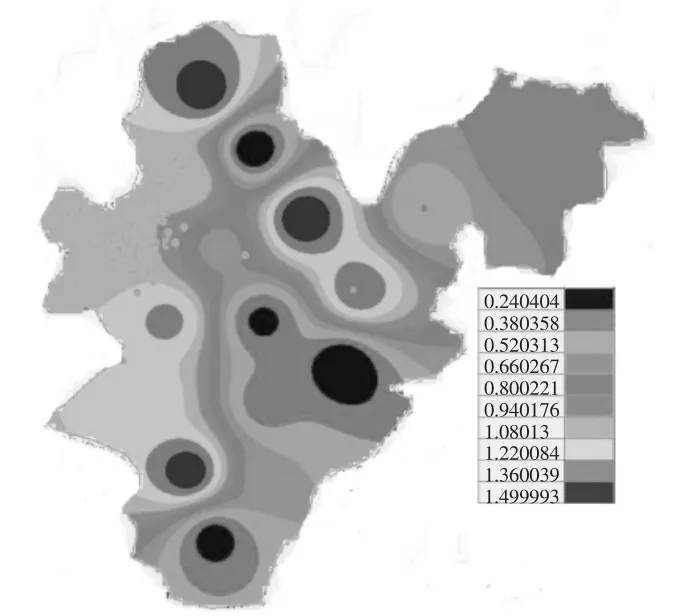
图9 研究区第5含水层渗透系数分布

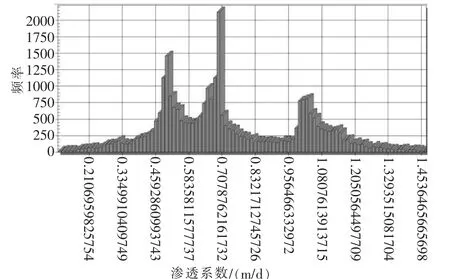
图10 研究区第5含水层渗透系数大小频率

3.4 计算结果分析

经过反演可得到第3层含水层水平方向渗透系数均值1.44m/d，最大值1.96m/d，最小值0.210m/d；第4含水层的渗透系数0.976m/d，最大值1.49m/d，最小值0.103m/d；第5含水层的平均渗透系数0.773m/d，最大值1.48m/d，最小值0.100m/d。从渗透系数反演计算结果可知，研究范围内不同含水层及同一含水层的不同地段的渗透系数并不一致，有的甚至相差比较大。从计算结果云图中可以发现监测井较为密集的地区反演的渗透系数值变幅较小。根据前期工程勘测资料及室内研究可知各地层的渗透系数如表1。

表1 部分试验土样的渗透系数

反演结果与室内试验所得渗透系数对比如图11。

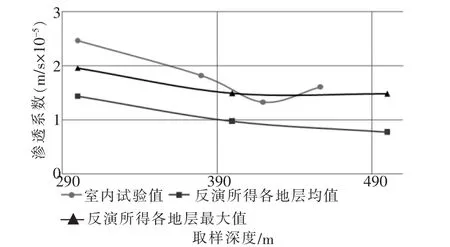
图11 各地层渗透系数反演与试验结果对比

从图11中可以看出，反演所得值与试验值变化趋势相对一致，由于从现场钻孔获取地下300～500m土样会引起土样扰动，因此室内试验所得渗透系数偏大，排除此方面干扰，可得反演所得值较为精确可靠。

4 结语

（1）本文所研究含水层主要为地下300～500m层位，地质参数难以确定，因此首先要对几个主要含水层的渗透系数进行反演。在参数反演过程中引进卡尔曼滤波算法，并运用该算法对观测井所获得的水头值进行同化过滤，并把同化后的水头值代入地下水分析软件，对所研究含水层的渗透系数进行了参数反演。

（2）通过反演计算得到第3含水层到第5含水层的渗透系数，计算结果表明各个含水的渗透系数不相同，并且同一含水层不同地方也相差较大，其中，第3含水层到第5含水层水平方向渗透系数均值分别为 1.44，0.97，0.77m/d，最大值分别为1.96，1.49，1.48m/d，最小值分别为0.2，0.1，0.1m/d。

（3）最后通过反演所得300～500m各地层渗透系数值与室内试验研究所得渗透进行对比分析，发现数据同化后再进行反演所得值比较精确可靠。

［1］邵景力，赵宗壮，崔亚莉，等.华北平原地下水流模拟及地下水资源评价［J］.资源科学，2009，31（3）：361-367.

［2］谢先红.基于数据同化方法的水文地质参数反演与变量估计［A］.北京力学会第十六届学术年会论文集［C］.2010.

［3］陈彦，吴吉春.含水层渗透系数空间变异性对地下水数值模拟的影响［J］.水科学进展，2005（4）：482-487.

［4］施小清，吴吉春，袁永生.渗透系数空间变异性研究［J］.水科学进展，2005（2）：210-215.

［5］Kalman R E.A new approach to linear filtering and prediction problems［J］.Transactions of the ASME-Journal of Basic Engineering，1960，82（series D）：35-45.

［6］Yan Chen， Dongxiao Zhang.Data assimilation for transient flow in geologic formations via ensemble Kalman filter［J］.Advances in Water Resources， 2006，29（8）：1107-1122.

［7］Liu C S， Chen Y， Zhang D X.Ivestigate of flow and transport processes at the MADE site using ensemble Kalman filter［J］.Advances in water resources，2008，31（7）：975-986.

［8］Huang C L， Hu B， Li X， et al.Using data assimilation method to calibrate a heterogeneous conductivity field and improve solute transportprediction with an unknown contamination source［J］.Stochastic Environmet Research and risk Assessment，2009，23（8）：1155-1167.

［9］Evensen G.The Ensemble Kalman Filter： theoretical f ormulation and practical implementation［J］.Ocean Dynamics，2003， 53（4）：1616-7228.

［10］Burgers G， Jan Van Leewen P， Evensen G.Analysis scheme in the ensemble kalman filter ［J］.Monthly weather review，1998，126（6）：1719-1724.

［11］南统超，吴吉春.集合卡尔曼滤波估计水文地质参数的局域化修正［J］.水科学进展，2010（5）：613-621.

［12］崔凯鹏，吴吉春.观测数据时空密度对集合卡尔曼滤波计算精度的影响［J］.水利学报，2013（8）：915-923.

［13］崔凯鹏.集合卡尔曼滤波在地下水流及溶质运移数据同化中的应用探讨［D］.南京：南京大学，2013.

［14］史良胜，杨金忠，李少龙，等.基于KL-Galerkin解法的地下水流动随机分析［J］.四川大学学报（工程科学版），2005（5）：31-35.

［15］宋雪航，史良胜，杨金忠.基于集合卡尔曼滤波的潜水动态预测方法［J］.武汉大学学报（工学版），2014（3）：324-331.

［16］林琳，史良胜，宋雪航.地下水参数反演的确定性集合卡尔曼滤波方法［J］.武汉大学学报（工学版），2016（2）：161-167，172.

Back analysis of geological parameters based on data assimilation

QIN Yao-jun1， ZHOU Xiao-yong2， YANG Ya-bin1， JIA Chao2
（1.NO.2 Hydro-engineering Geology Brigade of Shandong Provincial Bureau of Geology， Dezhou 253072， China；2.School of Civil Engineering， Shandong University， Jinan 250061， China）

Monitoring data of water level of observation wells are calculated by data assimilation technology and Calman filtering algorithm.With this method，the permeability coefficient of the main aquifer is inversed base on the accurate water level values，and compared with the permeability coefficient obtained by test.The results show that the inversion parameter after data assimilation and filtering is more accurate and effective.

data assimilation； Kalman filtering； permeability coefficient； parameter inversion

P64 文献标识码：B 文章编号：1672-9900（2017）06-0078-05

2017-08-22

秦耀军（1964-），男（汉族），山东济宁人，高级工程师，主要从事水文地质、工程地质、环境地质、地灾防治研究工作，（Tel）18561188280。

王艳肖）