Kriging法在区域重力场插值中的适用性研究

张永奇,韩美涛,韩晓飞,郑增记,翟宏光

(1.陕西省地震局，陕西 西安 710068；2.中国地震局地质研究所 地震动力学国家重点实验室，北京 100029)

Kriging法在区域重力场插值中的适用性研究

张永奇1,2,韩美涛1,韩晓飞1,郑增记1,翟宏光1

(1.陕西省地震局，陕西 西安 710068；2.中国地震局地质研究所 地震动力学国家重点实验室，北京 100029)

由于重力观测网点位分布不均匀，密度不够，在精细刻画区域重力场变化时受到很大限制，因此需采用合理的插值算法。文中介绍Kriging插值算法和变异函数理论模型的基础上，结合陕西地区2011—2012年离散重力变化数据，利用最小二乘法得到各个理论变异函数模型的拟合参数，并将实验变异函数模型用于Kriging插值算法，同时综合考虑交叉验证精度统计、插值精度统计结果，以此来研究Kriging插值算法的适用性，研究结果表明：基于最小二乘法获得的球形模型、指数模型拟合参数精度高，高斯模型、对数模型精度最差；基于球形模型、指数模型的实验变异函数用于Kriging插值算法得到的插值结果精度最高、图像平滑自然、异常区明显，是一种适合陕西地区重力离散数据进行插值计算的有效算法。

Kriging法；变异函数模型；陕西地区；重力场；插值

重力资料在地震长期预测预报中占有重要地位，合理的重力网布设是获取真实可靠资料的基础。但由于重力网布设易受各种因素的限制，点位分布往往呈现不均匀、密度不够等特点，这对于精细刻画某个区域重力场变化来说，显得力不从心。因此，针对离散观测值采用合理的插值算法进行插值计算就成为一个重要的解决途径。目前，重力场插值应用较多的算法有最小二乘配置法、样条函数法、Kriging法等[1-3]。Kriging法是一种依据已知点进行空间插值的地质学统计方法，该方法是由南非矿产地理学家P.G.Krige最先提出，该法综合考虑空间点的结构性和随机性，估值具有最优、线性、无偏等特点，在地学领域得到广泛的应用，并取得很好的效果[4-9]。目前，基于Kriging法进行数据插值的研究主要集中在几种插值算法的比较，研究表明Kriging法具有明显优越性[3,6,9-10]；基于不同变异函数的Kriging法进行重力场插值的研究相对较少。变异函数是Kriging法进行插值的核心，常用的变异函数理论模型有球面模型、高斯模型、指数模型等[12-14]，变异函数模型选择是否恰当，直接影响插值效果的好坏，甚至影响计算结果的可靠性，因此对不同变异函数模型的适用性进行研究，有利于提高Kriging法插值的精度和可靠性。基于上述分析，本文在介绍Kriging法及变异函数模型的基础上，以陕西区域离散重力变化数据作为研究对象，对基于不同变异函数的Kriging法插值结果进行精度统计，以此评价变异函数模型的适用性，最终得到适合该区域重力场插值的可靠算法。

1 数据处理理论与模型

1.1 普通Kriging法

假定Z(x)服从二阶平稳假设，其在空间位置x1,x2,…,xn有n个观测值Z(xi),i=1,2,…,n,则在未知点x0处，其观测值Z(x0)可由已知的n个观测值Z(xi)估计。

(1)

式中:λi为待定的权重系数，为达到线性无偏估计，使估计方差最小，权系数λi可由Kriging方程组决定。

(2)

式中:μ是拉格朗日乘数;γij表示第i,j个观测点间向量所对应的变异函数值;γi0表示第i个观测点到估值点间向量对应的变异函数值，这些量可通过实验变异函数拟合理论模型计算得到。在式(2)约束条件下，求出λj，再回代式(1)，即可根据已知点观测数据内插出待定点的观测估值[14]。

1.2 变异函数

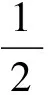
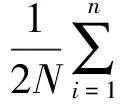
(3)

式中:γ*(h)为理论变异函数值γ(h)的估计值;N为被向量h相隔的实验数据对的数目。

按式(3)计算出空间相距h距离的变异函数值γ*(h)后，再选择合适的变异函数理论模型进行拟合，进而求出适合研究区域的变异函数理论模型。

1.3 变异函数理论模型

变异曲线图表示的是一定滞后距h的变异函数值γ*(h)与该h的对应图，如图1所示。图中C0称为块金效应，表示h很小时两点x和x+h之间空间信息的变化；a称为变程，其大小反映了研究对象中某一区域变化量的变化程度。CS称为总基台值，反映了某区域化变量在研究范围内变异的强度，它是最大滞后距的可迁移性变异函数的极限值，当h→∞时，γ(∞)=C(0)=Var[Z(x)]=CS，即当h→∞时，变异函数值近于先验方差C(0)，当无块金效应C0时，CS=C，当有块金效应时，CS=C+C0；而C称为基台值，它是先验方差与块金效应(常数)之变差，C=CS-C[14]。

图1 变异曲线图

变异函数理论模型分为有基台值和无基台值两大类。其中有基台类模型包括球形模型、高斯模型、指数模型、纯块金模型、线性模型(有基台)，有基台模型一般认为区域变量满足二阶平稳假设；无基台类模型包括幂函数模型、对数模型、线性模型(无基台)等，一般认为只满足本征假设[14]。具体模型如下：

1)球面模型:

(4)

2)高斯模型:

(5)

3)指数模型:

(6)

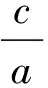
4)纯块金效应模型:

(7)

该模型对纯随机变量才适用。

5)有基台的线性模型:

(8)

6)幂模型:

γ(h)=hθ,0<θ<2.

(9)

当θ=1，即为无基台线性模型，γ(h)=ah,h>0，a为常数。

7)对数模型:

γ(h)=log(h).

(10)

由于h→0时，log(h)→-∞，这与变异函数性质不符合，因此在区域化变量为离散点时不适用。

利用式(3)求出各γ(h)，按最小二乘拟合法求出式(4)～式(10)中的参数C0，C，a，则可确定出样本空间的实验变异函数模型,也就是适合研究区域的变异函数模型[11-14]。

2 实例及结果分析

2.1 研究区概况

本文选取陕西地区2011～2012年离散重力变化数据作为研究对象，重力网范围为32.42°～36.25°N，106.15°～110.56°E，总共包括221个点，其中关中地区测点密度最大，平均点间距约10～15 km；陕南地区测点密度次之，平均点间距约20～30 km；陕北地区点位分布最为稀疏，平均点间距达到40～50 km。陕西地区地形地貌差异较大，陕北地区以黄土塬为主，海拔大致为800～1 300 m；关中地区为断陷盆地，平均海拔约520 m；陕南地区为秦巴山地，海拔基本上为1 500～2 000 m。为了同时顾及点位分布不均以及地形差异的影响，本文选择Kriging法对离散观测值进行插值，其目的既考虑观测值的空间性也考虑观测点间的相关性。通过对不同变异函数模型的参数进行拟合，获得不同的实验变异函数，并将其用于Kriging插值算法，通过精度对比分析，得到可靠性和精度都比较满意的Kriging插值算法。

2.2 研究结果与分析

首先利用研究区分布的211个离散点数据，建立适合本研究区的实验变异函数。根据离散点空间分布特征及其相关性，获得实验变异函数参数，具体参数见表1。由表1知，变异函数最大滞后距为1.9°，滞后组数划分为25组，滞后宽度为0.076°，变异函数高值、滞后方向、滞后方向公差分别为644、60°、90°。其次求取变异函数模型参数，选择变异函数理论模型(球形模型、指数模型、幂函数模型、块金效应模型等)，并给定初始参数值，利用最小二乘拟合法对各模型参数进行迭代处理，设置迭代次数为50，经过计算获得各组合变异函数模型(块金效应+其它模型)参数并绘制拟合图，如表2、图2所示。表2中参数就是实验变异函数模型所需的参数C0，C，a，将参数代入模型(4)～模型(10)，就可以获得适合研究区的变异函数模型，根据模型(1)～模型(3)就可以求取研究区任一点的重力异常值。从图2直观可知，球形模型、指数模型、线性模型、幂函数模型拟合效果较好，高斯模型、对数模型拟合效果较差，研究表明对数模型不适合进行离散点拟合[15]。

表1 实验变异函数参数

表2 不同变异函数模型拟合参数

备注：线性模型斜率slope=225;幂函数模型因变量θ=0.692

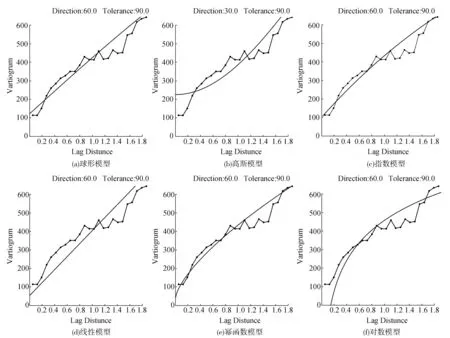
图2 不同模型的变异函数拟合图

为了进一步比较不同变异函数模型的适用性，采用交叉验证的方法进行分析。将221个离散点数据全部作为检核点，计算拟合点值与离散数据点值的残差精度以及拟合点自身精度，精度统计如表3所示。分析表3发现，从拟合点的均方根来分析，精度从高到低顺序为：高斯模型>指数模型>球形模型=幂函数模型>线性模型>对数模型；但从拟合点值与离散数据点值的残差均方根来分析，精度从高到低顺序为：球形模型=幂函数模型>线性模型>指数模型>高斯模型>对数模型；从标准差来分析，也可以得到和均方根大致相同的结论，因此综合4个精度指标考虑，球形模型、幂函数模型拟合精度较高，更加适合研究区离散数据Kriging法插值，而高斯模型、对数模型拟合精度最差。

表3 不同变异函数模型的交差验证精度统计

利用上述各个实验变异函数模型进行Kriging法插值，总共获得8 700个节点的插值数据，纬度方向插值节点为100行，经度方向插值节点为87列。根据插值结果绘制插值等值线图，超出插值边界最大值的数据采用白化值，如图3所示，图3中(a)～(f)分别代表球形模型、高斯模型、指数模型、线性模型、幂函数模型、对数模型的插值结果。同时统计基于不同变异函数模型对应的Kriging法插值精度，具体统计指标有插值花费时间、插值最大值、最小值、均值、标准差，具体见表4。从图3直观看出，(a)、(c)～(e)结果较好，很好地体现了重力场异常变化的细节特征，是对离散观测值的有效插值和拟合，而(b)、(f)插值效果最差，(b)反映的是研究区的趋势变化，其中的细节体现不完整，而(f)完全不适合离散点插值，对重力场异常变化反映不明显，而且量值远远大于采用其它模型进行插值的结果。从细节上分析，基于球形模型和指数模型的插值结果，“牛眼”较少，曲线比较光滑，由南向北过渡比较自然；而基于线性模型和幂函数模型的插值结果反映细节比较清晰，形成很多局部异常，因此基于这两种模型得到的插值结果最好是进行高通滤波，得到更加真实的异常变化图。

由表4知，几种模型花费的时间差别不大，对数模型用时最多，精度最差。从插值的最大、最小值来看都没有超过原始离散点的最大值72.7、最小值-52.7，表明插值数据可靠性较高，只进行内插计算没有外推计算。从标准差来看高斯模型精度最高，但这是一种“虚假”的高精度，并不适合研究区的重力异常插值；其余5种模型中球形模型和指数模型精度较高，与图3结果表现一致，是真实反映插值效果的指标；幂函数模型、线性模型精度稍差，应该是局部区域插值精度差导致的。

表4 不同变异函数模型的插值精度统计

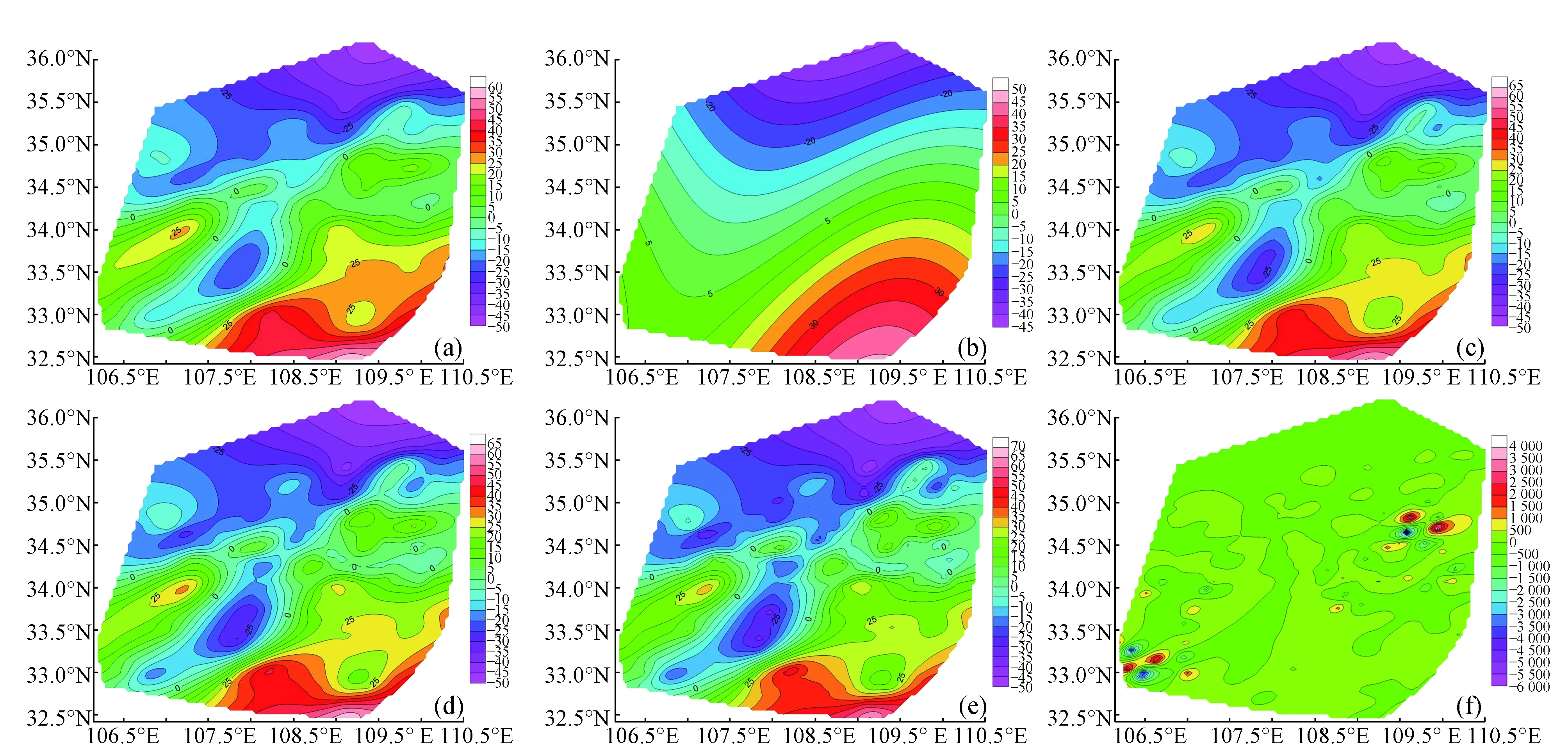
图3 基于不同变异函数模型的kriging重力场插值图(ugal)

3 结 论

本文针对陕西地区2011～2012年211个离散重力变化值，基于不同变异函数模型构建Kriging插值法进行模型适用性研究，得出如下结论：

1)对于本次试验数据，最大滞后距为1.9°，滞后组数分为25组，滞后方向为60°；经反复测试变异函数模型选择纯块金模型和其它模型的组合，拟合效果较好，单独模型拟合效果不佳；且利用最小二乘拟合迭代计算，迭代次数设置为50次，基本上可以获得最优解。

2)利用最小二乘拟合获得的各种模型的参数差异较大，同时发现数据具有一定程度的各向异性，量值皆为2，各向异性方向变化范围为15.61°～16.33°。变异函数模型参数精度统计使用交叉验证方法，交叉验证时采用全部离散点数据，其优点是避免由于选择部分离散点而带入人为的统计偏差。交叉验证结果显示球形模型、幂函数模型精度最高，均方根和标准误差均最小，说明这两种模型建立参数选取合理，适合用于陕西地区离散重力变化网格化插值。

3)利用基于不同变异函数模型的Kriging法进行插值时，考虑插值曲线的光滑性，整个研究区域划分为8 700个节点，插值得到各个节点的重力变化值。为了减小边缘效应的影响，超出插值最大值的区域采用白化值。由图3、表4可以得出：采用高斯模型、对数模型的Kriging法进行插值效果最差，不适合陕西地区离散重力变化插值；插值效果最好的是采用球形模型、指数模型，精度最高、误差最小、图像显示曲线光滑自然，且没有出现插值外推现象。

[1] 祝意青，胡斌，李辉，等.用双三次样条函数模拟青藏高原东北缘重力场动态图像[J].中国地震，2005，21(2)：165-171.

[2] 祝意青，陈斌，张希，等.景泰5.9级地震前后的重力变化研究[J].中国地震，2001，17(4)：356-363.

[3] 李振海，汪海洪.重力数据网格化方法比较[J].大地测量与地球动力学，2010，30(1)：140-144.

[4] 陈小斌.中国陆地现今水平形变状况及其驱动机制[J].中国科学(D辑：地球科学)，2007，37(8)：1056-1064.

[5] 朱守彪，蔡永恩，石耀霖,等.青藏高原及邻区现今地应变率场的计算及其结果的地球动力学意义[J].地球物理学报，2005，48(5)：1053-1061.

[6] 曾怀恩，黄声享.基于Kriging方法的空间数据插值研究[J].测绘工程，2007，16(5)：5-8.

[7] 刘晓刚，吴晓平，王宝军，等.卫星重力梯度数据的网格化方法研究[J].大地测量与地球动力学，2010，30(6)：60-65.

[8] 刘晓霞，江在森，武艳强，等.Kriging方法在GPS速度场网格化和应变率场计算中的适用性[J].武汉大学学报(信息科学版)，2014，39(4)：457-461.

[9] 刘兆平，杨进，武炜，等.地球物理数据网格化方法的选取[J].物探与化探，2010，34(1)：93-97.

[10] 姚道荣，钟波，汪海洪，等.最小二乘配置与普通Kriging法的比较[J].大地测量与地球动力学，2008，28(3)：77-82.

[11] 熊俊楠，马洪滨.变异函数的自动拟合研究[J].测绘信息与工程，2008，33(1)：27-29.

[12] 李章林，王平，李冬梅，等.实验变差函数计算方法的研究与运用[J].国土资源信息化，2008(2)：10-14.

[13] 郭泉河，李秀海.不同变异函数的泛Kriging法的GPS高程拟合结果[J].黑龙江工程学院学报(自然科学版)，2011， 25(4)：26-28.

[14] 沈云中，陶本藻.实用测量数据处理方法[M].北京：测绘出版社，2012：194-214.

[15] 侯景儒，尹镇南，李维明，等.实用地质统计学[M].北京：地质出版社，1998：31-68.

Research on the applicability of Kriging methodin regional gravity field interpolation

ZHANG Yongqi1,2, HAN Meitao1, HAN Xiaofei1, ZHENG Zengji1，ZHAI Hongguang1

(1. Shaanxi Provincial Earthquake Administration, Xi’an 710068,China;2. State Key Laboratory of Earthquake Dynamics，Institute of Geology, China Earthquake Administration，Beijing 100029，China)

Because the gravity observation network distribution is not uniform and the point density is not enough, it is very limited to describe the variation of regional gravity field, which needs to use the reasonable interpolation algorithm. Based on the detailed introduction of the Kriging interpolation algorithm and the variation function theory, this paper unifies the Shaanxi area 2011～2012 discrete variation of gravity data, obtains the fitting parameters of theoretical variation function model by least square method, and uses the experimental variation model for Kriging interpolation algorithm. Considering the cross validation accuracy statistics, the interpolation precision results, the application to study Kriging interpolation algorithm, the result shows that: the fitting parameter accuracy of spherical model and exponential model are high based on the least square method, and the accuracy of Gauss model and logarithmic model is the worst; the experimental variation function based on the exponential model and spherical model used in the Kriging interpolation algorithm, can get the highest accuracy of interpolation, meanwhile the image is smooth and the abnormal area is obvious, so it is a suitable interpolation calculation algorithm for gravity discrete data of Shaanxi area.

Kriging method；variation function model；Shaanxi area；gravity field；interpolation

2016-10-28

2016年度中国地震局“三结合”课题(162704)；陕西省起航与创新基金资助项目(201514)

张永奇(1985-)，男，工程师,博士研究生.

著录：张永奇,韩美涛,韩晓飞，等.Kriging法在区域重力场插值中的适用性研究[J].测绘工程，2018，27(2)：1-6.

10.19349/j.cnki.issn1006-7949.2018.02.001

P207

A

1006-7949(2018)02-0001-06

张德福]