自同构群的阶等于其阶两倍的有限p-群

2018-01-09马玉龙刘海林

重庆理工大学学报(自然科学) 2017年12期

关键词：自同构题设子群

伍星，马玉龙，刘海林

(云南大学数学与统计学院，昆明 650091)

自同构群的阶等于其阶两倍的有限p-群

伍星，马玉龙，刘海林

(云南大学数学与统计学院，昆明 650091)

假设G是一个有限非循环p-群,并且G的阶大于p2,如果 |G| 整除 |Aut(G)|,则称群G为LA-群。考虑了满足 2|G|=|Aut(G)| 的有限p-群G,其中p≠2，分类了满足这一条件的某些有限p-群类。

有限p-群；LA-群；中心商；中心自同构

1 背景

假设G是一个有限非循环p-群,并且G的阶大于p2,如果 |G| 整除 |Aut(G)|,则称群G为LA-群。对LA-群的研究已有很久的历史。现在列出关于LA-群的一些结果。假设G是一个阶为pn的有限非循环p-群,且n>2。如果G满足下列条件之一，则G是LA-群。

1)G是一个PN-群B和一个交换群P的直积,并且 |B| 整除 |Aut(G)|(见文献[2]);

2)G的幂零类cl(G)=2(见文献[4]);

3)G是p-交换p-群(见文献[5]);

4)p>2,并且G是亚循环的(见文献[6]);

5)p>2,并且G/Z(G) 是亚循环的(见文献[7]);

6)n≤7(见文献[89]);

7) |G|≤29(见文献[10]);

8)p>2,并且G是有限的模p-群(见文献[11]);

9) Frattini子群Φ(G) 循环(见文献[3]);

10)G是一个指数为p2的循环子群(见文献[12]);

11)G是一个极大类p-群(见文献[2]);

12) 对任意的α∈G/Z(G),αZ(G)⊆αG(见文献[13]);

13) |G/Z(G)|≤p4(见文献[1]);

14)G是余类为2的p-群(见文献[14])。

本文考虑了满足以下两个条件的p-群G，其中p≠2：

1) 2|G|=|Aut(G)|;

2)G是极大类的，或者G具有循环的Frattini子群。

2 预备引理

本节给出一些必要的预备结果。

对于有限循环p-群G，已经熟知有 |Aut(G)|p=|G|/p。对于其他的有限交换p-群,有下面的结果。

引理1([15，Theorem 2.3])假设G是一个阶为pn的非循环的交换群，其中n≥4，则下列事实成立：

1)G满足 |Aut(G)|p=|G|，当且仅当G是 (n-1,1) 型的；

2)G满足 |Aut(G)|p=p|G|，当且仅当n=4 并且G是 (2,2) 型的；

3) 其他情形均有 |Aut(G)|p≥p2|G|。

引理2([15，Theorem 3.3])假设G是一个有限的极大类p-群,其阶 |G|=pn,其中n>4，则 |Aut(G)|p>|G|。

引理3([15，Theorem 3.4])假设G是一个有限的极大类p-群，则G满足|Aut(G)|p=|G|，当且仅当G是一个阶为p3的非交换群，或者G同构于下列p4阶群之一:

1)S81=〈x,y,z|x9=y3=z3=1,[x,y]=x3,[x,z]=y,[y,z]=1〉;

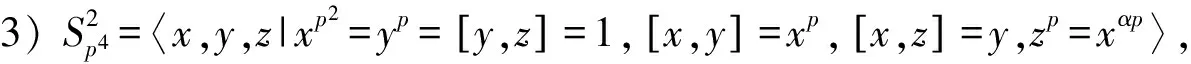
4)S16=〈x,y|x8=y2=1,[x,y]=x2〉。

3 定理证明

Malinowska在文献[15]中完整地描述了满足 |Aut(G)|p=|G| 的交换或者极大类的有限p-群G。下面将分类非循环p-群G,其满足下列条件：G是交换的、极大类的,超特殊的或者具有循环的Frattini子群Φ(G)，并且 2|G|=|Aut(G)|。

定理1 假设G是交换p-群,|G|=pn(n>2,并且p≠2)，则不存在G满足2|G|=|Aut(G)|。

证明假设G是一个阶为pn的交换p-群，并且满足 2|G|=|Aut(G)|。但是由引理1有p=2,故与题设矛盾。

下面的命题是文献[17]的一个结果的推广。

定理2 假设G是一个阶为pn的超特殊p-群，则不存在G满足 2|G|=|Aut(G)|。

证明假设G是一个超特殊p-群,并且满足 2|G|=|Aut(G)|。假设p是奇素数，则p-1 整除 |G| 显然不可能。从而p=2,与题设矛盾。

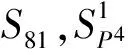
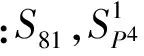
定理4 假设G是一个非交换p-群,|G|=pn,并且其Frattini子群Φ(G) 循环。如果G满足 2|G|=|Aut(G)|,则Z(G) 是循环的,并且有 |G/Z(G)|=p2。

[1] DAVITT R M.On the automorphism group of a finitep-group with a small central quotient[J].Can.J.Math,1980,32(5):1168-1176.

[2] OTTO A.Central automorphisms of a finitep-group[J].Duke Math,1966,125(2):280-287.

[3] FOULADI S，JAMALI A R,ORFI R.On the automorphism group of a finitep-group with cyclic Frattini subgroup[J].Mathematical Proceedings of the Royal Irish Academy,2008,108A(2):165-175.

[4] FAUDREE R.A note on the automorphism group of a group[J].Proceedings of the American Mathematical Society,1968,19(6):1379-1382.

[5] DAVITT R M.The automorphism group of finitep-abelianp-groups Ill[J].Journal of Mathematics,1972,16:76-85.

[6] DAVITT RM.The automorphism group of a finite metacyclicp-group[J].Proc.Am.Math.Soc,1970,25:876-879.

[7] DAVITT R M,OTTO A D.On the automorphism group of a finitep-group with the central quotient metacyclic[J].Proc.Am.Math.Soc,1971,30:467- 472.

[8] EXARCHAKOS T.Onp-group of small order[J].Publ.Inst.Math,1989,45:73-76.

[9] GAVIOLI N.The number of automorphisms of groups of order p 7[J].Proc.Roy.Irish Acad.Sect,1993(A2):177-184.

[10] FLYNM J,MACHALE D,O’BRIEN E A O’Brien.Finite groups whose automorphism groups are 2-group[J].Proc.Roy.Irish Acad.Sect,1994(A2):137-145.

[11] DAVITT RM,OTTO A.On the automorphism group of a finite modularp-group[J].Proc Am Math Soc,1972,35:399- 404.

[12] XIAO C C.A conjecture on the automorphism group of a finitep-group[J].Rend Circ Mat Palermo Suppl,1990(23):347-351.

[13] YADAV M K.On automorphisms of finitep-groups[J].J.Group Th,2007,10:859-866.

[14] FOULADI S,JAMALI A R,ORFI R.Automorphism groups of finitep-groups of coclass 2[J].J Group Th,2007(10):437- 440.

[15] MALINOWSKA I.Finite p-groups with fewp-automorphisms[J].J Group Th,2001(4):395- 400.

[16] ATTAR M S.On equality of order of a finitep-group and order of its automorphism group[J].Bull Malays Math Sci Soc,2015,38:461- 466.

[17] WINTER D L.The automorphism group of an extraspecialp-group[J].Rocky Mt J Math,1972,2(2):159-168.

AFinitep-GroupWhoseOrderofItsAutomorphismGroupisEqualtoTwiceItsOrder

WU Xing, MA Yulong, LIU Hailin

(School of Mathematics and Statistics, Yunnan University, Kunming 650091, China)

finitep-group; LA-group; central quotient; central automorphism

2017-05-20

国家自然科学基金资助项目(11301468,11231008); 云南省自然科学基金资助项目(2013FB001)；云南大学第八届研究生科研创新项目

伍星，硕士研究生，主要从事有限群、代数图论研究；通讯作者刘海林，男，硕士，主要从事有限群、代数图论研究，E-mail：hailinliuqp@163.com。

伍星，马玉龙，刘海林.自同构群的阶等于其阶两倍的有限p-群[J].重庆理工大学学报(自然科学)，2017(12):189-191.

formatWU Xing, MA Yulong, LIU Hailin.A Finitep-Group Whose Order of Its Automorphism Group is Equal to Twice Its Order[J].Journal of Chongqing University of Technology(Natural Science)，2017(12):189-191.

10.3969/j.issn.1674-8425(z).2017.12.032

O152.1

1674-8425(2017)12-0189-03

(责任编辑杨黎丽)