基于宽频导波检测锚杆脱粘缺陷的数值仿真

王 娜，张伟伟，常 红

(太原科技大学 应用科学学院，太原 030024)

基于宽频导波检测锚杆脱粘缺陷的数值仿真

王 娜，张伟伟，常 红

(太原科技大学 应用科学学院，太原 030024)

将低频超声导波应用于在役锚杆脱粘的无损检测，难点在于锚杆与周围介质的相互影响，使导波的传播具有复杂性，从而增加了导波信号分析的难度。将选择宽频信号为激励信号，首先对宽频信号在深埋锚杆中的传播特性进行分析，然后将测试信号进行小波包分解，发现不同的缺陷形式对宽频信号中不同频段的响应具有明显的特征。但由于脱粘缺陷和响应信号特征之间并不是单调关系，因此结合BP神经网络技术，建立测试信号与缺陷特征之间的对应关系，来实现对锚杆脱粘缺陷检测。最后，分析不同噪声水平对识别结果的影响。文中方法对于噪声水平小于5%的检测信号，具有较好的识别结果。

锚杆；宽频导波；无损检测;小波包；神经网络

近年来，锚杆在矿山、公路、水利水电等建设工程中的应用十分广泛[1-5]。锚杆作为一种受力的构件，且大部分的锚杆锚固属于隐蔽工程，因此对其进行安全性检测具有一定的难度。人们对锚杆锚固质量进行检测时，采用的方法是拉拔法,这种方法具有破坏性，不适合实地检测，因此研究和开发锚杆施工质量的新型无损检测方法越来越受到研究人员和工程技术人员的关注[6-7]。1978年，瑞士的HF.Thurner[8]在检测砂浆锚杆锚固的质量时做了大量研究，并提出了超声波检测方法。到了80年代末，美国矿业局研制了一种基于发射和接收超声波原理的顶板锚杆粘结力测定仪[9]。近年来，李义[10-11]等人对应力反射波法进行了研究，主要是把锚杆进行了分段，找出了锚杆低端反射显现，更重要的是研究出锚杆自由端长度与波长之间存在的定量关系，并且证明了应力反射波的速度范围，这一范围是介于锚杆杆体波速和锚固介质波速之间的。许明[12]在进行锚杆的无损检测时，运用了岩石声波测试技术，通过对锚杆的振动效应的测定，来估计和判断锚杆的极限承载力，并将小波分析和神经网络等信号分析处理技术应用到了较复杂检测信号的分析中。鉴于超声导波具有可沿结构长度方向传播，检测距离长，并可同时检测结构内部和表面缺陷的特点，超声导波已广泛应用于在役管道[13-14]、金属板[15-16]以及钢轨[17-18]等材料的无损检测。但由于导波的频散特性，使得导波在检测的过程中对各类缺陷的敏感性不同，因此需要预先选定导波的模态，所以确定激励频率成为一个关键问题，而此项工作的盲目性比较大，所以这个选择的过程也给人们带来了很大的困惑，人们最后尝试着通过多次反复的试验来确定最佳激励模态以及最佳激励的频率，这样不仅会耗费大量时间、精力，而且硬件资源问题也是很难解决的。但如果找一种宽频信号[19]来作为激励信号，那么就可以获得在其频带范围内的任意的单频激励信号所对应的响应，需要预先选定相应模态以及相应频率的问题也迎刃而解。将采集的信号进行小波包分析和神经网络的训练，构成一个适用于锚杆无损检测的神经网络[20-22]。而到目前为止，基于神经网络对锚杆锚固质量的研究主要是针对锚杆灌浆密实度以及锚杆有无缺陷，并不能对锚杆的缺陷位置进行定位，若能进一步对锚杆的缺陷位置进行定位，将为工程中锚杆的无损检测带来极大的方便。

采用宽频导波应用于在役锚杆的脱粘无损定位检测，其难点在于锚杆与周围介质将相互影响，使导波的传播具有复杂性，增加导波信号分析的难度。通过研究宽频信号在埋深锚杆中传播特性分析，并将测试信号利用小波包分解，发现不同缺陷形式对宽频信号中不同频段的响应具有明显的特征。但由于缺陷和响应信号特征之间并不是单调关系，因此，结合BP神经网络技术，建立了测试信号与缺陷特征之间的对应关系，从而实现了锚杆的缺陷检测。

1 数值模拟

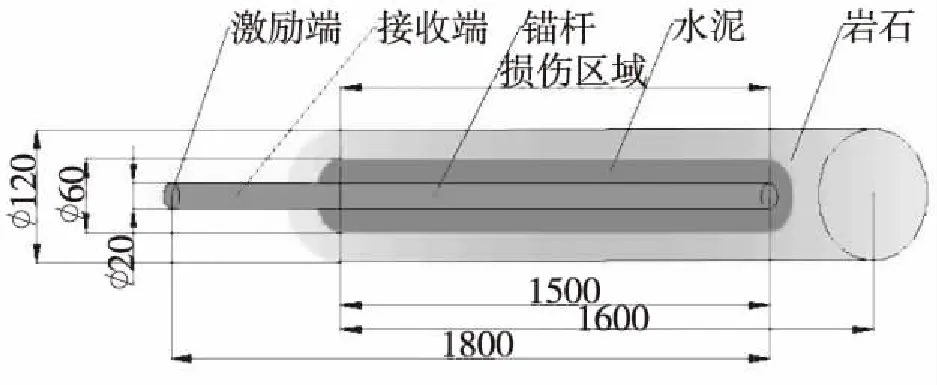
图1 锚杆示意图(单位： mm)Fig.1 Anchor schematic (unit:mm)

如图1所示，利用ANSYS-LSDYNA采用SOLID164单元对此模型进行有限元数值模拟。选用锚杆模型为全长砂浆锚固岩石锚杆，锚杆直径为0.02 m，全长1.8 m，锚固段长度为1.5 m，外露长度为0.3 m，锚固的介质是水泥砂浆，砂浆层厚度为0.02 m，周围介质为岩石，模型边界条件设置为右端固定且此次数值模拟锚杆使用非预应力锚杆。为了能够获得较为准确的数值仿真响应结果，对缺陷周围区域进行了网格细化。在工程上锚杆的塑形变形较大会导致锚杆失效，并且当锚杆处于工作段时，其塑形变形一般很小，是可以忽略不计的，因此本文将锚杆当作线弹性体，材料的其它参数如表1：

在锚杆顶端施加扫描宽频信号激励波f(x)，f从10 kHz到100 kHz，步长取1 kHz，信号持续时间为0.614 ms.在外露端0.01 m处进行接收。激励波信号如式(1)所示，图2为此激励波信号时域和频谱分析图。

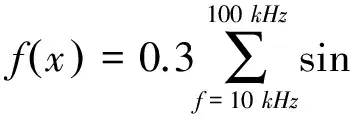
(1)

表1 材料的力学参数

Tab.1 The Material mechanics parameters

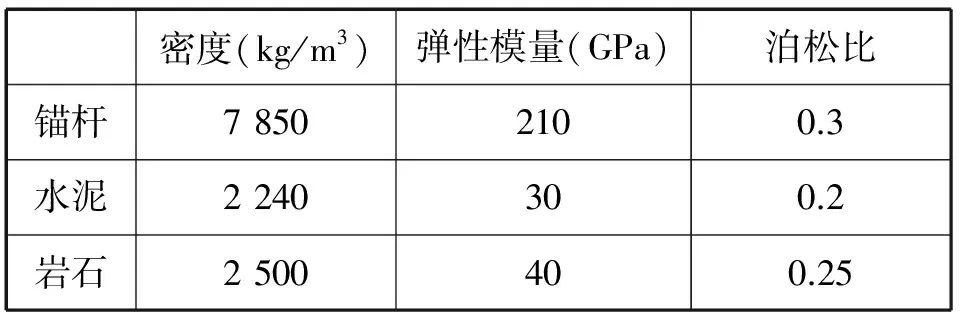
密度(kg/m3)弹性模量(GPa)泊松比锚杆78502100．3水泥2240300．2岩石2500400．25

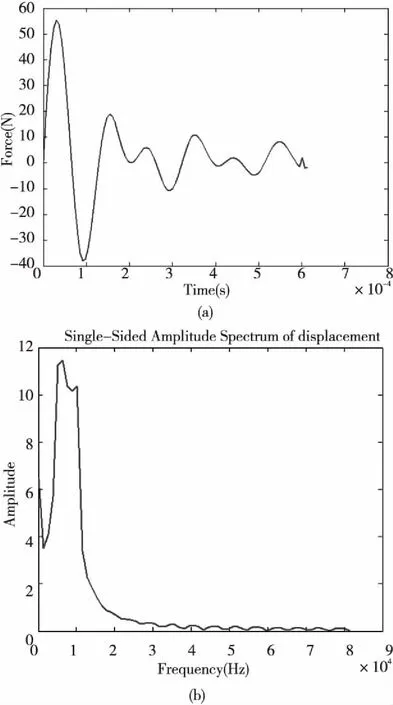
图2 激励信号的时域和频谱分析图Fig.2 Excitation signal in the time domain and frequency spectrum analysis

锚杆与水泥之间产生剥离将引起测试信号的变化，不同剥离状态对不同频率的信号敏感特性不同，因此可根据这一特性进行剥离状态识别。本文将结合BP神经网络，利用锚杆超声导波检测信号进行剥离位置识别。选用同一种锚杆，锚杆损伤均为环向剥离，改变剥离位置。在长度方向将埋入部分自左向右平均划分为10区域，各区域长0.15 m.为了获得足够的训练样本，各损伤区域内再平均划分10种缺陷，每处缺陷长0.015 m，总计测试100组数据。为了简便，将每种算例标记为 (i-j)，其中，i表示缺陷区域且i=I,II,…X，j表示缺陷区域内的工况编号且j=1,2,…10.利用ANSYS-LSDYNA动力学分析模块进行求解，设置求解步长为5×10-6，图3(a)和(b)分别给出了完好算例和算例 (VII-7)(即损伤区域VII中第7种工况)以及算例(IV-6)的时域结果比较图。

由上图可以看出，对于不同的损伤情况，其测试信号会存在一定的差别，但很难直接依据测试信号识别锚杆缺陷，因此需要对测试信号进行进一步的分析处理。采用小波包分解可以对信号进行高、低频分解，从而获得不同缺陷对不同频率信号的响应特征，依此来进行缺陷识别。鉴于该目的，将得到的测试信号进行小波包分解，利用各频段的信号能量构造神经网络的输入向量，通过训练，从而获得适用于锚杆无损检测的神经网络。

2 小波包分解与神经网络

当锚杆埋入部分存在缺陷时，由于位置不同必将引起不同频率信号的改变。小波包分析可以同时对信号进行低频、高频分解，考虑到锚杆中不同缺陷形式对不同频率的敏感特性，采集各种工况下的超声导波信号，将信号进行小波包4层分解，得到16个频带。 图4 (a)、(b)、(c)、(d)分别描述的算例I-7，III-9，VI-4，VII-6与完好锚杆的各个频带内能量对比图。

从图中可以看出：在频带2,7,11,12以及15,16内，有缺陷锚杆比完好锚杆的能量值小，而在其它频带内，有缺陷锚杆比完好锚杆的能量值大。对不同缺陷的锚杆检测信号进行小波包分解后，相同频带内信号的能量有着明显的区别，这说明损伤对不同的频率范围具有显著的敏感性，为了进一步对缺陷进行损伤定位，本研究将利用神经网络建立不同损伤特征与小波能谱之间的关系。

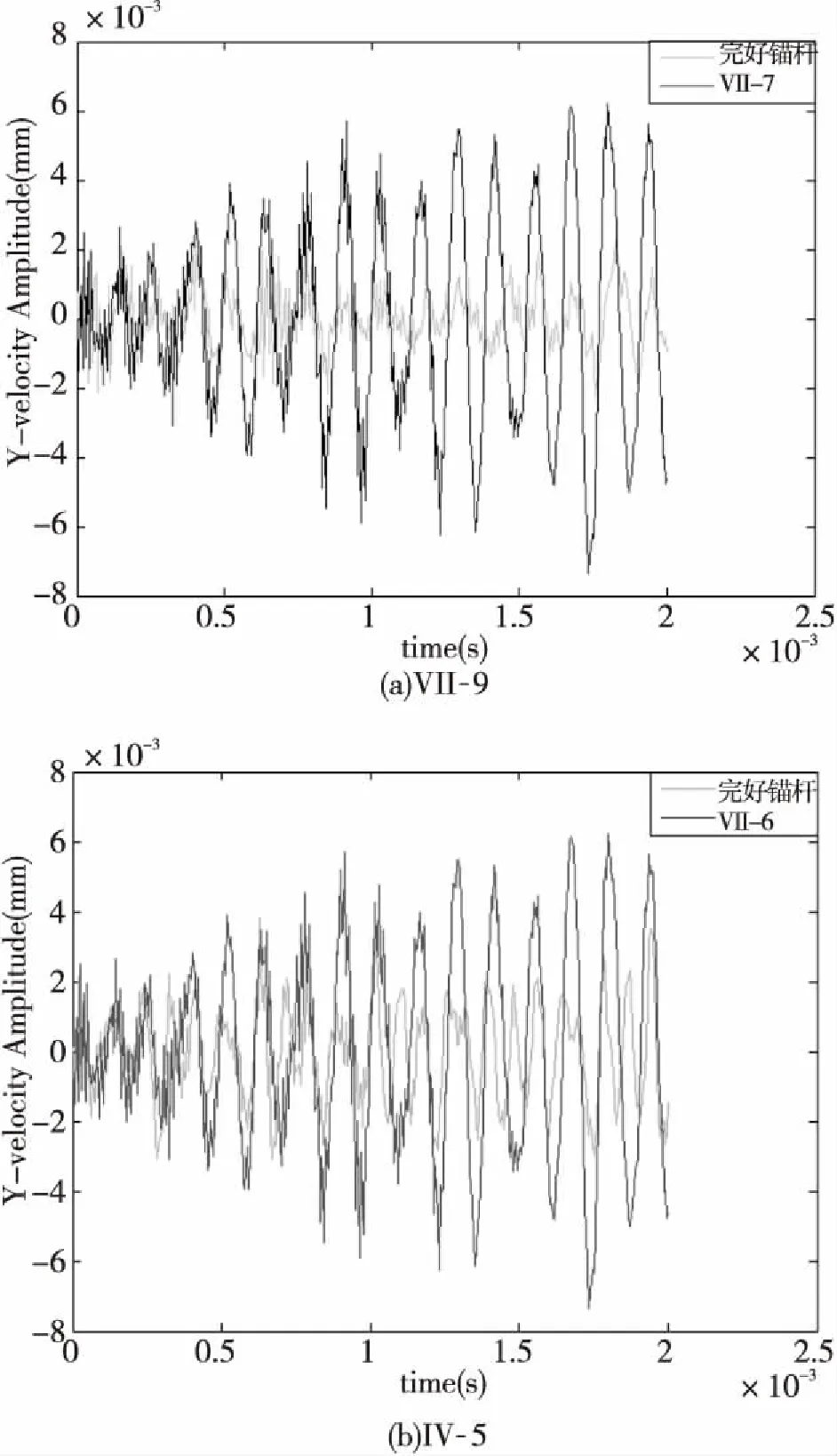
图3 算例VII-9和 IV-5时域结果图Fig.3 The time domain results of VII-9& IV-5

神经网络的学习主要包括有导师学习和无导师学习两种模式。有导师学习主要是在训练期间有外部老师告诉网络每个输入向量应该对应的输出向量，目的就是减少实际输出向量和预期输出向量之间的误差。而无导师学习是指在没有任何进一步指导的情形下，构建其内部表征，在网络内部对其性能进行自适应调节。锚杆的无损检测需要输入向量对应相应的输出，本文将采用BP神经网络来进行训练。

将锚杆反射信号进行4层小波包分解，且其能量作为神经网络的输入向量。以锚杆缺陷位置定义ψm作为输出向量，本例中由于设置损伤为10个区域，所以m=1,2,3…10. 且向量ψm输出向量为10个分量，假设第i个区域有损伤，则设输出向量中第i个参数为1，其余分量均为0，如式(2)：

(2)

图4 完好锚杆和有缺陷锚杆的能量对比图 Fig.4 The comparison of energy between perfect and defective anchor

3 神经网络的训练

小波包分解后每个频带内的能量eni如式(3)：

(M=1,2....k,k∈N)

(3)

式中：n——缺陷编号，N——分解层数，M——每个频带内的速度幅值个数。

将eni作为网络输入层神经元，ψm作为网络输出层神经元。一般情况下，三层网络就可以很好地去解决一般模式的识别问题[23]。建立锚固系统无损检测的BP神经网络模型，其中tansig()为隐含层神经元的传递函数，logsig()为输出层神经元传递函数。如图5所示。

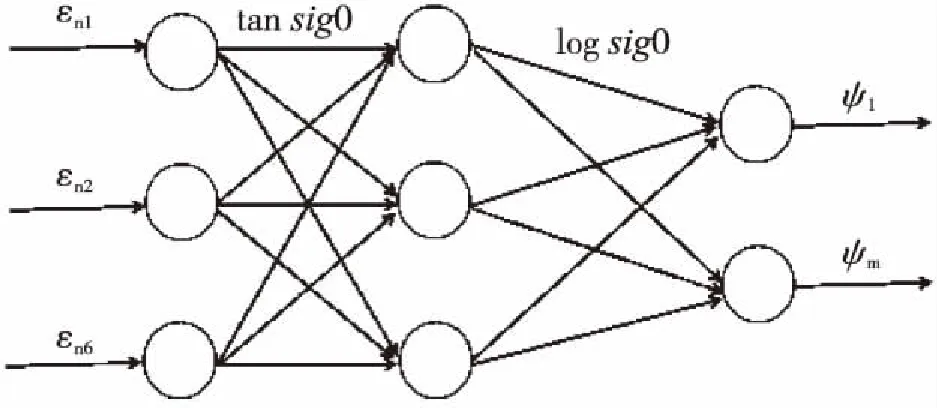
图5 BP神经网络模型Fig.5 The BP neural network model

这里隐含层的神经元个数n2与输入层的神经元个数n1之间有如下的近似关系[23]，

n2≈2n1+1

(4)

针对于本例，按照下列方式来进行神经网络的设计，网络的输入层神经元个数为16个，输出层神经元个数为10个，隐含层的神经元个数依据式(5)近似为33个，设其初始为33.此次网络训练，隐含层的神经元是经过实际训练的检验来不断调整的，以满足最后的需要。

在神经网络的训练过程中，设定均方误差函数如式(5)：

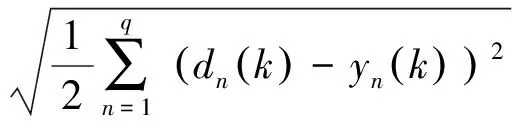
(5)

dnk表示输出层第n个节点的期望输出，ynk表示网络实际输出，q表示输出神经元个数。进行网络训练后，如图6为此BP神经网络预测模型的训练过程误差曲线。

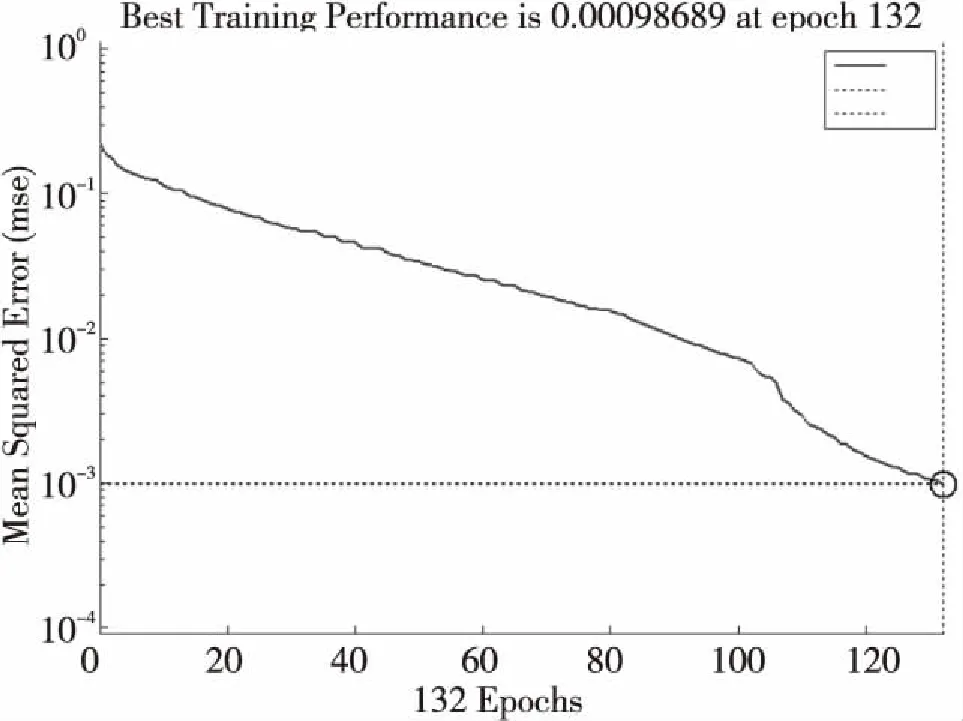
图6 误差变化曲线Fig.6 The error of curve

由图6可以看出，该模型在经过132次训练之后达到设定误差值。经过不断调整，最后确定隐含层的神经元个数为35时，训练的网络就基本可以达到要求。经过多次试验得出，在误差设定值为0.001时，该BP神经网络模型具有良好的损伤识别检验性，网络的性能达到要求。

4 损伤识别

为了验证所训练的网络可进行剥离区域识别，利用上述训练好的BP神经网络对任意的收集到数据进行预测。而在实际工程应用中，在信号获取和传输过程中会有噪声影响，考虑式(7)描述的噪声模型:

s'=s+EpσsN

(6)

其中，s'表示含噪声信号，s表示动态响应信号，N表示满足(0,1)正态分布的随机数组，σs表示动态响应信号s的标准方差，EP表示噪声水平。随机抽取前述10个损伤区域中任意两种工况，添加5%的噪声，并将其作为验证算例。其识别结果如表2所示。其中Dii=1,2,3...10表示损伤在第i区域。由表2可知，I-8的预期输出应该为区域I，而实际输出为区域I，通过分析其他缺陷区域的预期与实际输出，可知在一定的噪声水平范围内有良好的识别结果。再以损伤在区域I中的数据I-8与和区域VII中的数据VII-9为例，分别添加1%，3%，5%，7%，10%的噪声，识别结果如表3.

表2 加噪网络预测结果

Tab.2 The predicted results after adding noise by network

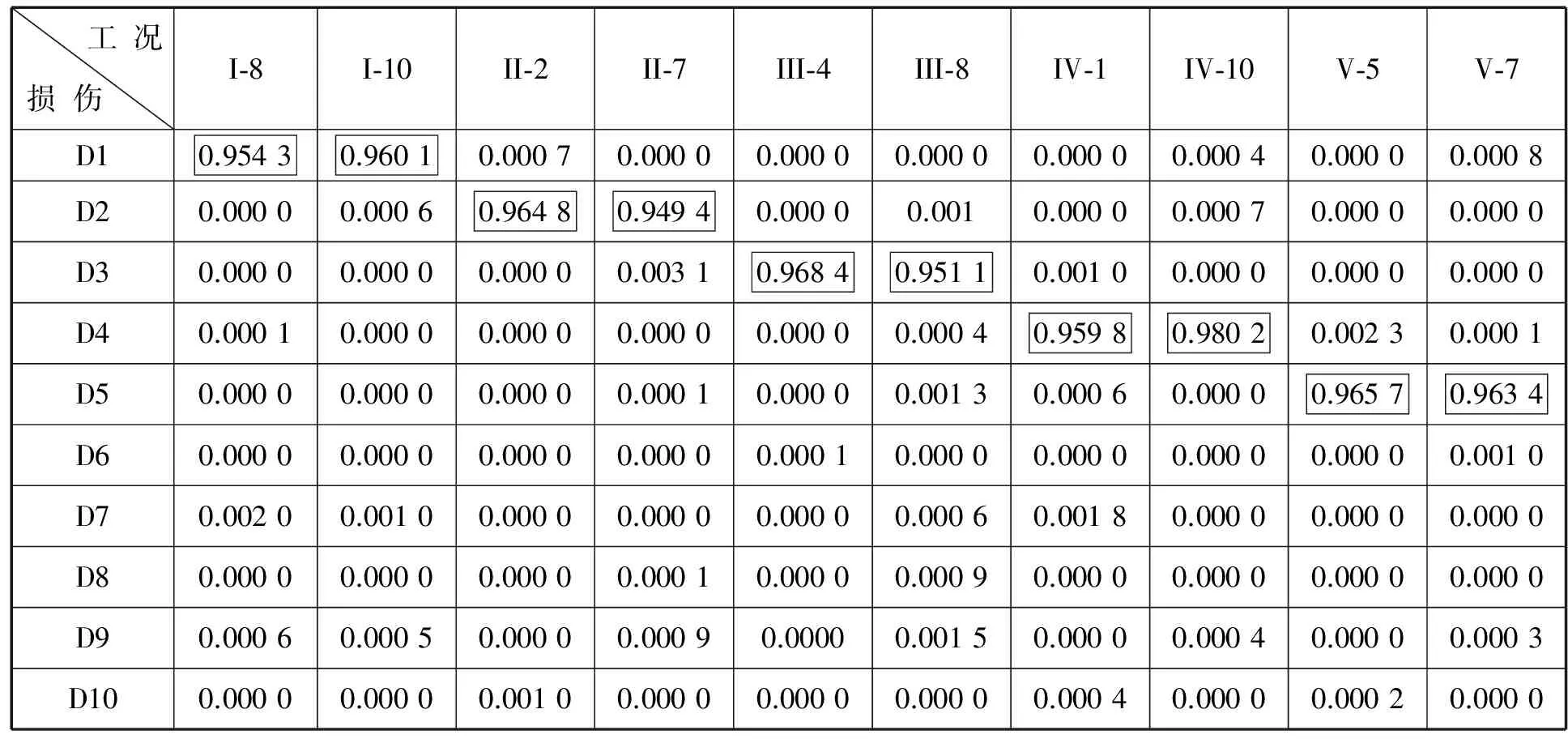
工况损伤I⁃8I⁃10II⁃2II⁃7III⁃4III⁃8IV⁃1IV⁃10V⁃5V⁃7D10．95430．96010．00070．00000．00000．00000．00000．00040．00000．0008D20．00000．00060．96480．94940．00000．0010．00000．00070．00000．0000D30．00000．00000．00000．00310．96840．95110．00100．00000．00000．0000D40．00010．00000．00000．00000．00000．00040．95980．98020．00230．0001D50．00000．00000．00000．00010．00000．00130．00060．00000．96570．9634D60．00000．00000．00000．00000．00010．00000．00000．00000．00000．0010D70．00200．00100．00000．00000．00000．00060．00180．00000．00000．0000D80．00000．00000．00000．00010．00000．00090．00000．00000．00000．0000D90．00060．00050．00000．00090．00000．00150．00000．00040．00000．0003D100．00000．00000．00100．00000．00000．00000．00040．00000．00020．0000

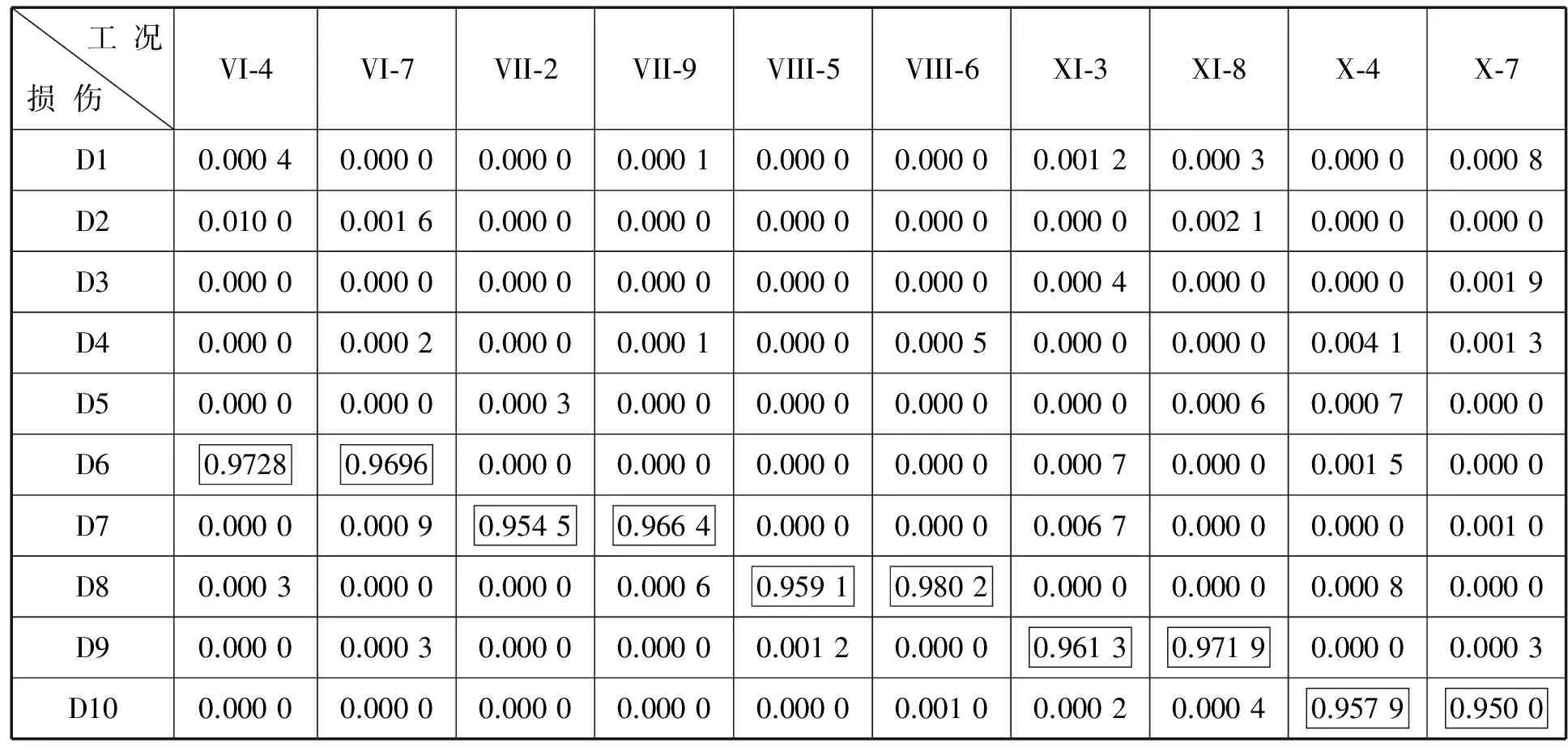
工况损伤VI⁃4VI⁃7VII⁃2VII⁃9VIII⁃5VIII⁃6XI⁃3XI⁃8X⁃4X⁃7D10．00040．00000．00000．00010．00000．00000．00120．00030．00000．0008D20．01000．00160．00000．00000．00000．00000．00000．00210．00000．0000D30．00000．00000．00000．00000．00000．00000．00040．00000．00000．0019D40．00000．00020．00000．00010．00000．00050．00000．00000．00410．0013D50．00000．00000．00030．00000．00000．00000．00000．00060．00070．0000D60．97280．96960．00000．00000．00000．00000．00070．00000．00150．0000D70．00000．00090．95450．96640．00000．00000．00670．00000．00000．0010D80．00030．00000．00000．00060．95910．98020．00000．00000．00080．0000D90．00000．00030．00000．00000．00120．00000．96130．97190．00000．0003D100．00000．00000．00000．00000．00000．00100．00020．00040．95790．9500

表3 I-8与VII-9在不同噪声水平下预测结果对比

Tab.3 The prediced results of I-8&VII-9 under the different noise levels

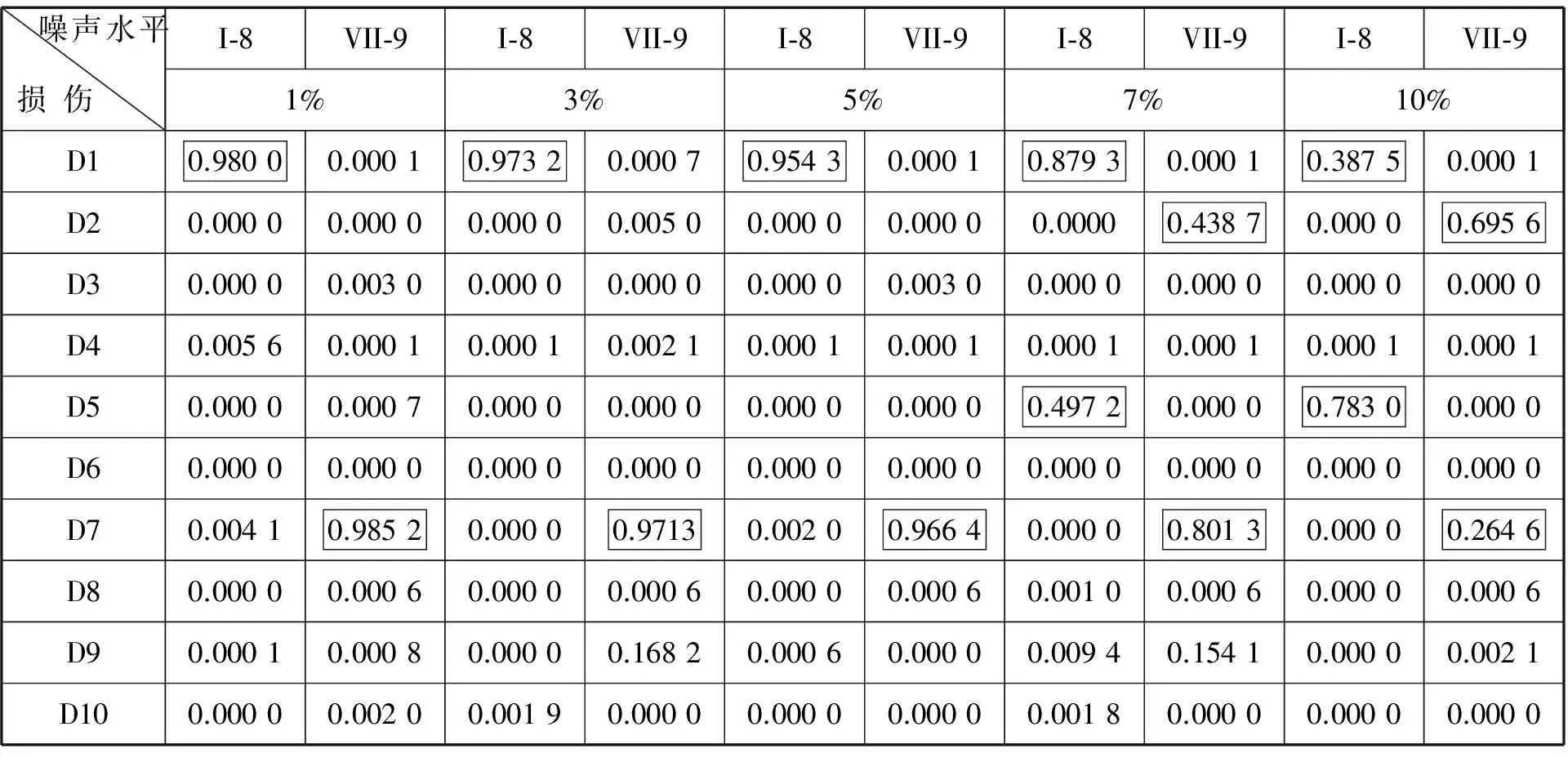
噪声水平损伤I⁃8VII⁃9I⁃8VII⁃9I⁃8VII⁃9I⁃8VII⁃9I⁃8VII⁃91%3%5%7%10%D10．98000．00010．97320．00070．95430．00010．87930．00010．38750．0001D20．00000．00000．00000．00500．00000．00000．00000．43870．00000．6956D30．00000．00300．00000．00000．00000．00300．00000．00000．00000．0000D40．00560．00010．00010．00210．00010．00010．00010．00010．00010．0001D50．00000．00070．00000．00000．00000．00000．49720．00000．78300．0000D60．00000．00000．00000．00000．00000．00000．00000．00000．00000．0000D70．00410．98520．00000．97130．00200．96640．00000．80130．00000．2646D80．00000．00060．00000．00060．00000．00060．00100．00060．00000．0006D90．00010．00080．00000．16820．00060．00000．00940．15410．00000．0021D100．00000．00200．00190．00000．00000．00000．00180．00000．00000．0000

由表3可知，当噪声水平为7%与10%时，I-8实际输出区域为I、V，而与预期输出区域的I不对应，VII-9的实际输出区域为II、VII，与预期输出区域VII也不对应，可知损伤识别结果不好。

通过多组计算实验，得出在噪声水平超过5%时，损伤识别结果不佳。因此，在一定的噪声水平范围内，该BP网络对锚杆无损检测的预测模型合理，锚杆缺陷预测数据可靠，可以用于工程中对锚杆剥离缺陷的定位识别。

5 结 论

结合小波包分解和BP神经网络发展了一种宽频超声导波检测锚杆锚固完整性的无损检测方法，从锚杆动态响应信号的收集到小波包分解再到能量特征向量的提取，最后将这些特征向量输入人工神经网络进行训练，其结果表明：锚杆锚固质量可由宽频信号的不同频带敏感性进行检测。噪声水平不超过5%时，该方法可获得较好的识别结果，实现了对锚杆脱粘缺陷的定位识别。数值算例验证了锚杆无损检测的合理性。

[1] GUO ZHI-BIAO，WANG JIONG，ZHANG YUE-LIN. Failure mechanism and supporting measures for large deformationof Tertiary deep soft rock[J]. International Journal of Mining Science and Technology，2015 (25):121-126.

[2] 林观茂,张丽娟,温忠义.深基坑扩大头锚杆支护体系数值模拟[J]. 路基工程，2015(5):92-98.

[3] 田鹏,李波. 锚杆支护在水利水电工程地下厂房施工中的应用[J]. 黑龙江水利科技，2014，42(4):170-171.

[4] VAN D，MEERS L，DONNELLY P，et al.Automated bolting and meshing on a continuous miner for roadway development[J]. International Journal of Mining Science and Technology，2013(23):55-61.

[5] 张嘉林.锚杆挡土墙施工技术在高速公路边坡中的应用[J]. 华东公路，2015(1):82- 83.

[6] 许明,张永兴,阴可. 某隧道锚杆完整性的无损检测方法[J]. 土木工程学报，2004,37(5):78-81.

[7] WANG MING-WU，WANG HE-LING. Nondestructive testing of grouted bolts system [J]. Chinese Journal of Geotechnical Engineering，2001.23(1):109-113.

[8] THURNER H F. Boltometer-Instument for nondestructive testing of grouted rock bolts[C]// International Symposium on Filed Measurements in Geomechanics. Rotterda-m:A. A. Balkema Publishers，1988:135-143.

[9] 许煜东,王军平,尹学林. 锚杆无损检测技术实验研究[J]. 水电勘测设计,2003(2):19-22.

[10] 王成,挥寿榕,李义. 锚杆-锚固介质-围岩系统瞬态激励的响应分析[J]. 太原理工大学学报，2000，31(6)165-168.

[11] 张昌锁，李义，赵阳升,等. 锚杆锚固质量无损检测中的激发波研究[J]. 岩石力学与工程学报，2006，25(6):1240-1245.

[12] 任智敏，李义.基于声波测试的锚杆锚固质量检测信号分析与评价系统实现[J].煤炭学报,2011,36(S1)191-196.

[13] SUN YA-JING，DAI BO. Research on ultrasonic guided wave testing pipeline corrosion based on wavelet transform[J].2013 25th Chinese Control and Decision Conference,2013.25:2802-2805.

[14] .武静.基于杜芬方程的超声导波检测方法研究[D].太原：太原科技大学,2014.

[15] JIAO JING-PIN，HE CUN-FU，WU BIN. Vibromodulation and guided wave techniques for contact defect detection in plate[J]. Chinese Junrnal of Acoustics，2011，30:33-43.

[16] 王永顺，周省三.激光在楔形金属板中激发超声导波的实验研究[J]. 淮海工学院学报:自然科学版,2011，20(3):15-18.

[17] 周建民,徐清瑶,李 鹏,等. 钢轨无损检测中的超声导波技术[J]. 仪表技术与传感器，2015(6):99-102.

[18] MARIANI S，NGUYEN T，PHILLIPS R R，et al. Noncontact ultra-sonic guided wave inspection of rails[J]. Structural Health Monitoring，2013(12):539-548．

[19] 邓菲，陈洪磊，张僖. 基于宽频激励的管型结构导波检测[J]. 机械工程学报，2014(18):23-28.

[20] 刘明贵,岳向红. 基于小波神经网络的锚杆锚固质量分析[J]. 岩石力学与工程学报，2006，25(1):83-87.

[21] ANAMIKA Y，ALEENA S. A single ended directional fault section identifier and fault locator for double circuit transmission lines using combined wavelet and ANN approach[J]. Electrical Power and Energy Systems，2015,69:27-33.

[22] 陈建功,李 昕,张永兴. 基于小波神经网络的锚杆围岩结构系统的识别[J]. 煤炭学报，2009，34(10):1333-1338.

[23] 张德丰.MATLAB神经网络应用设计[M].北京:机械工业出版社,2009.

NumericalSimulationoftheDefectionofAnchorDebondingDefectBasedonBroadbandGuidedWave

WANG Na, ZHANG Wei-wei, CHANG Hong

(College of Applied Science, Taiyuan University of Science and Technology,Taiyuan 030024, China )

The low-frequency ultrasonic guided wave was applied to debonding nondestructive testing of the anchoring bolt in service; the difficulty is that the bolt and the surrounding media will influence each other, so that the guided wave propagation is more complex, as well as increasing the difficulty of the analysis of the guided wave signal. The broadband signal was used as the excitation signal in this article, firstly, it is based on the broadband signal propagation characteristic of the anchor rod in the embedded depth, and the wavelet packet is used to decompose the test signal, it is obvious that the different defects have different frequency bands in the form of the broadband signal response characteristics. Because the defects and the response are not of monotonic relationship among the signal characteristics, therefore, combining wavelet packet decomposition and neural network, the corresponding relation between test signal and damage characteristics is established to realize the defect detection of the anchor. Furthermore, the tested pollution by noise was also used to identify the anchor integrity. The simulation showed an excellent identified results when noise level is less than 5%.

anchor bolt， broadband guided wave， nondestructive detection，wavelet packet， neural network

1673-2057(2018)01-0069-08

2016-09-06

山西省自然科学基金(2013011005-3);山西省青年科技研究基金(2015021017)；太原科技大学科技创新项目(20145008)

王娜(1988-)，女，硕士研究生，复合材料断裂理论及结构设计；通讯作者:常红教授，Email:wyxwww@sohu.com

O3

A

10.3969/j.issn.1673-2057.2018.01.013