ANSYS在真空炉温度场建模研究中的应用

王跃飞， 冯志强， 张圆圆， 雷金辉， 黄宜军

(1.钦州学院机械与船舶海洋工程学院, 广西 钦州 535000；2.昆明理工大学真空冶金国家工程实验室, 云南 昆明 650093)

ANSYS在真空炉温度场建模研究中的应用

王跃飞1， 冯志强1， 张圆圆1， 雷金辉2， 黄宜军1

(1.钦州学院机械与船舶海洋工程学院, 广西 钦州 535000；2.昆明理工大学真空冶金国家工程实验室, 云南 昆明 650093)

真空炉作为真空蒸馏法的主要设备，在二次资源再生、新材料的研发等方面应用广泛。与传统火法精炼除杂质相比较，真空蒸馏法具有步骤简单、直收率高、对环境无污染等优点。在实际生产中，因真空炉温度控制水平低、冶炼时炉内温度难采集等原因，其发展受到限制，因此对该设备进行温度场的仿真建模研究具有重要意义。本文采用ANSYS对内热式真空炉温度场的主要坐标点进行仿真计算，同时利用多组双铂铑高温热电偶对该炉测试实验，结果表明将有限元运用于真空炉瞬态温度场分析中，相对误差在2.536%～3.696%之间，仿真结果与实验测试结果基本一致。此研究为不同合金的冶炼提供了新的温度场分析方法。

建模； 温度场； 有限元分析； ANSYS软件； 真空炉

真空炉作为真空蒸馏分离多元合金的主要设备，在冶金工业中广泛应用。与传统火法精炼相比，真空蒸馏法具有步骤简单、回收率高，对环境无污染等优点[1]。真空炉反应区温度的准确性、温度场的分布情况以及反应过程的瞬时温度变化等因素，对不同金属在真空条件下的反应机理分析有着极其重要的作用[2]，同时也直接影响产品的质量、能耗和设备的使用寿命。对于真空冶金炉而言，影响指标除温度外，真空度、抽速容积比、炉室漏气率、加热功率、温度场均匀性等也是需要考虑的重要指标[3]，而且温度对其中的许多指标都有影响，甚至有决定性的影响，若不能准确掌握炉内温度的分布情况，则无法进一步了解与掌握各种金属冶炼过程的反应机理，也无法掌握真空冶金炉的工艺操作参数，造成人力、物力、财力的巨大损失和浪费，甚至产生安全事故[4]。本文对真空冶金炉温度场的仿真进行实验研究，为不同合金真空冶炼提纯时温度场的分布情况提供仿真方法和实验可行性数据。

1 ANSYS仿真

1.1 内热式真空炉模型的物理描述及炉况简化

实验设备采用内热式真空炉，该炉由蒸发盘、冷凝罩、供电系统、抽真空系统和水冷却系统等组成。石墨电柱作为加热源，安装于炉体中心位置，加热系统由PLC控制可控硅，从而控制加热电流的大小[5]。水冷却系统使炉体内部形成大梯度温度差，利于气相金属蒸气冷凝，达到分离合金、提炼金属的目的，并可降低炉壳温度，延长真空炉的使用寿命[6]。由于炉体主视图为轴对称图形，因此取右半边主视图作为仿真模型。真空炉尺寸如图1所示。

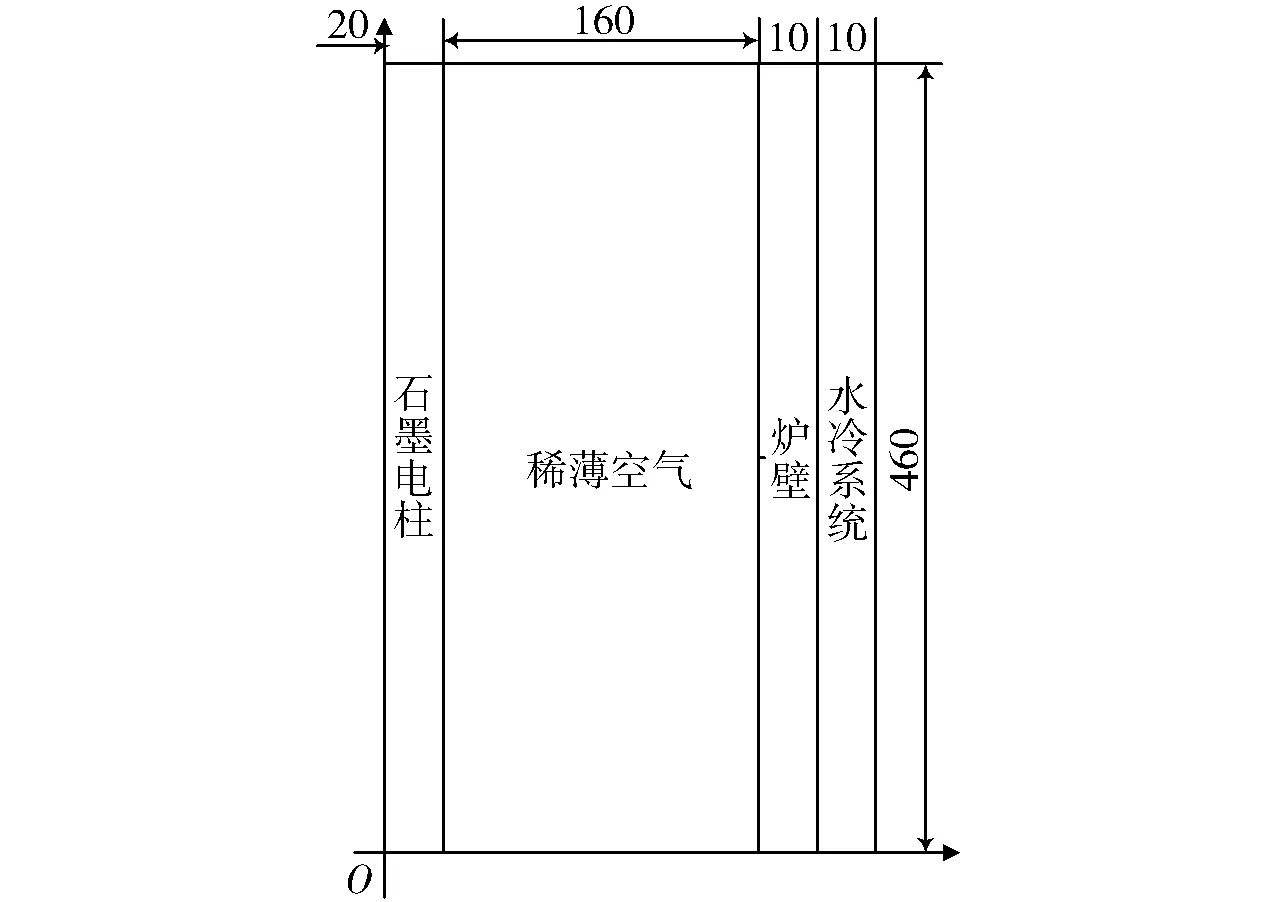
图1 真空炉尺寸图(右半主视图，单位mm)

实验表明，内热式真空炉工作区域呈圆柱空间，为得到炉内温度场的近似分布情况，仿真测试节点T1、T2、T3的分布如图2所示。

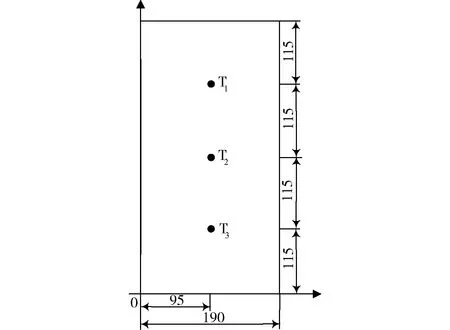
图2 炉内仿真测试节点分布图(单位mm)

由于该炉内部温度场由石墨电柱和炉壁之间的热辐射、石墨电柱和炉壁分别与稀薄空气之间的热传导叠加而成[7]。因此做如下假设和约定：①由于蒸发盘紧贴于石墨电柱周围，故将蒸发盘作为石墨电柱的一部分处理，只考虑炉侧壁与石墨电柱之间的热辐射。②石墨电柱高度近似等于炉体高度，认为石墨电柱和炉壁之间辐射换热角系数各处相等。

③反应区域稀薄空气分布均匀。④设定仿真环境压强为80 Pa[8]。

1.2 有限元模拟计算热传导的一般格式

瞬态温度是时间域和空间域的函数，在空间域中采用C型插值函数对有限元进行离散，利用加权余量法进行分部积分可得到瞬态有限元热传导一般格式为式(1)[9-10]。

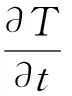
(1)

式中：K为热传导矩阵；T=[T1，T2，…Tn]T，为节点的温度矩阵；P为温度载荷矩阵；C为热容矩阵。

1.3 ANSYS仿真

图2给出真空炉反应区域及仿真测试节点分布模型，表1给出真空炉各部分材料属性及相关参数，以此作为仿真模型。ANSYS仿真过程主要步骤如下：

(1)设置相关材料参数[11]，如表1所示。

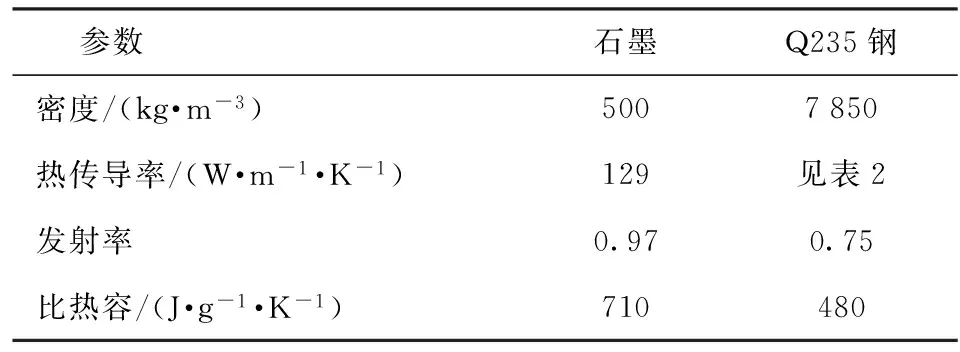
表1 相关材料参数

Q235钢在不同温度下的热传导率不同，因此在设定炉壁的材料参数时，将真空炉升温阶段内Q235钢热传导率数值相差较大的温度进行参数设置，表2为不同温度下Q235钢的热传导率[12]。

表2 不同温度下Q235钢的热传导率

(2)划分网格：对有限元模型选择单元类型，定义单元划分尺寸为0.005，然后作单元格划分，网格划分后如图3(a)所示。

(3)施加温度载荷及求解：设定初始环境温度为25 ℃，水冷系统温度为70 ℃，加热元件的最高温度为1 500 ℃。施加发射率载荷：石墨电柱为0.97，Q235钢为0.75。施加温度载荷：加热元件为T0=1 500 ℃，水冷壁为T1=70 ℃。定义数值：分别定义斯蒂芬- 玻尔兹曼常数为5.669×10-8，温度偏移量TOFFST=273，定义辐射求解选项中收敛公差为0.01，选择迭代求解算法，定义角度系数求解选项(做平面分析)。设置迭代次数为1 000(因为ANSYS默认的最大迭代次数为25，当迭代25次后还没有收敛，计算就会结束，因此需要加大迭代计算次数)。存盘后进行求解。

(4)结果的后处理：对所得的结果进行处理，获得达到稳态时的仿真温度场分布图，仿真计算结果温度分布如图3(b)所示。将温度沿炉体x=200 mm方向路径映射，拾取轴向三等分节点，如图3(c)所示。提取并显示该路径上三个节点的温度值，节点T1、T2、T3仿真计算结果如图3(d)所示。

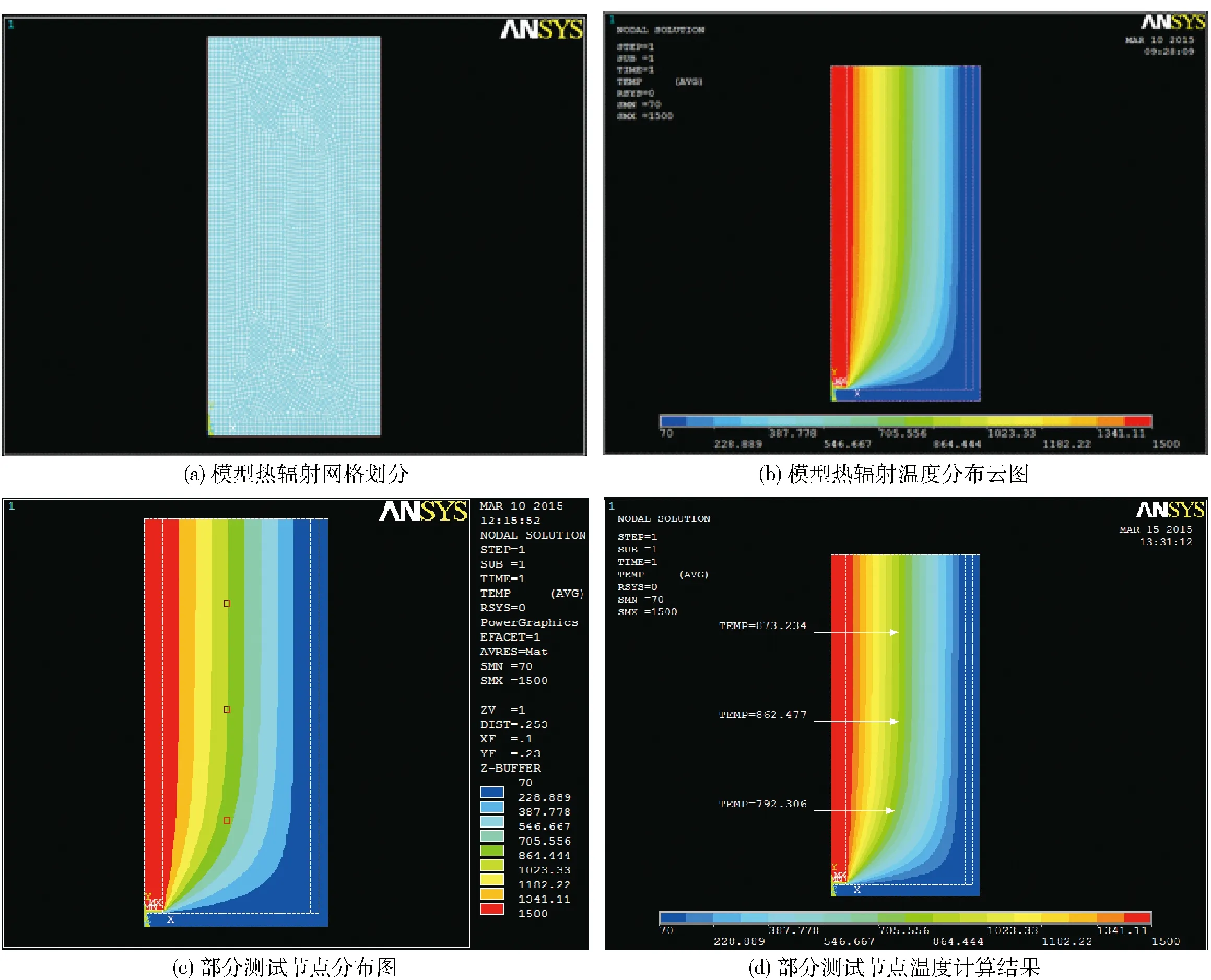
图3 真空炉模型热辐射温度仿真图(单位℃)

图3(b)所示的热辐射温度场分布云图表明：炉内反应区域温度场分布近似由石墨电柱到炉壁径向降低，从上至下温度呈降低趋势。由图3(d)可知，节点T1、T2、T3在保温阶段的仿真计算结果分别为873.234 ℃、826.477 ℃、792.306 ℃。

为了对上述仿真方法及模型的准确性进行验证，在昆明理工大学真空冶金国家工程实验室对内热式真空炉进行实验分析。

2 实验分析

按照图2所注的测试节点坐标分布尺寸，在内热式真空炉中安装15支双铂铑高温热电偶测量温度，通过西门子S7- 300控制器实现温度值的实时采集。实验获得15支高温热电偶所测得的从0到112 min，每2 min记录一次的温度数据。取安装于圆周上的12支热电偶，以上、中、下三个等温面将其分为3组：第1组T1(X2，X3，X5，X6)，第2组T2(X8，X9，X10，X11)，第3组T3(X13，X14，X15，X16)。分别将等温面T1～T3上的4支热电偶的测量值取平均值，得到等温面T1、T2、T3的温度曲线如图4所示。

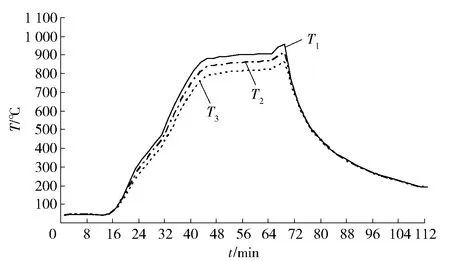
图4 内热式真空炉在0～112 min内等温面实测温度值曲线

图4所示的等温面实测温度曲线显示：在48～66 min段，炉膛内反应区域温度较为稳定，考虑到4组热电偶安装位置处于同一等温面，温度曲线走向基本一致，因此可以说明真空炉在48 min左右进入保温阶段，热电偶在50～58 min处于保温相对稳定时间段，三组热电偶测试的主要温度值数据见表3。

实测温度值在48～66 min内，真空炉反应区域温度较为稳定，为减小误差，取该时间段内曲线相对平滑的50～58 min段，三处节点所对应的5组数据，取平均值，并以公式：(测量值+修正值-模拟仿真值)/(测量值+修正值)计算相对误差，三个等温面实测值和仿真计算值如表4所示。

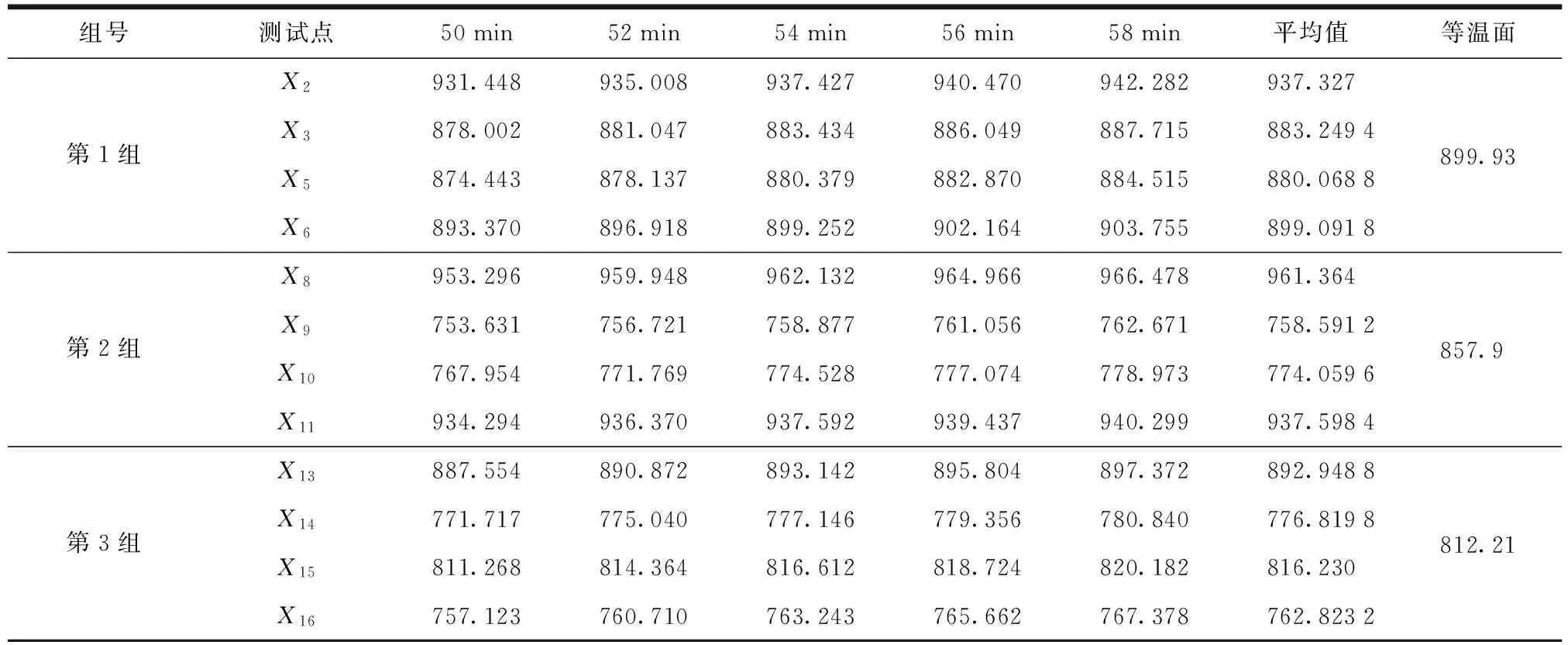
表3 三组热电偶测试的主要温度值 ℃

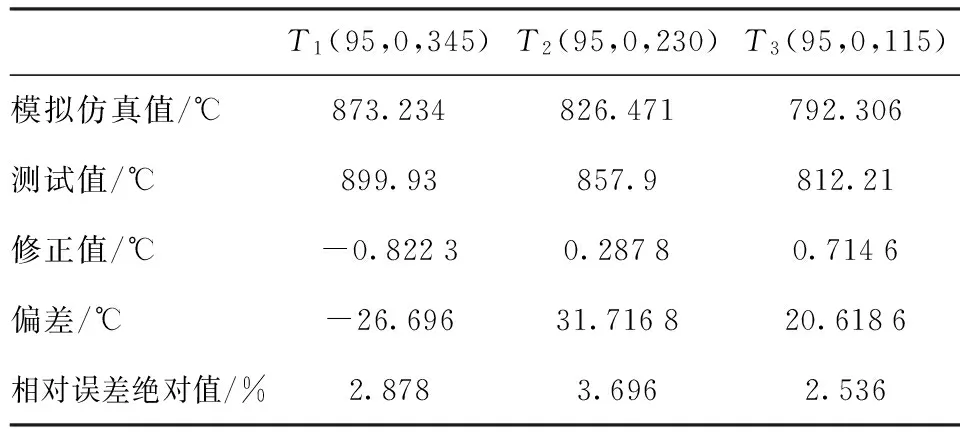
表4 三个等温面测试值和模拟仿真值

由表4知，三个等温面处的模拟仿真温度值与实验测试值最大相对误差为3.696%，最小相对误差为2.536%，平均相对误差为3.037%。其中在等温面T2和T3处，模拟计算值与实测值误差较T1偏大，经分析，造成此处数据偏大的原因：在实际测量中，T2和T3等温面上安装的4支热电偶可能插入过浅，偏离了坐标位置，造成测量温度值相比预期值偏低。但考虑到平均温度在误差接受范围内，且每组热电偶的温度曲线走势基本相同，因此实验所测数据基本可靠。

3 结论

运用ANSYS有限元分析方法，建立了真空炉温度场的仿真模型，计算出炉内主要节点的温度值。利用双铂铑高温热电偶对内热式真空炉对应节点进行测量验证，对实验数据处理后表明：等温面T1、T2、T3上的热电偶修正值分别为：-0.822 3 ℃、0.287 8 ℃、0.714 6 ℃。实验温度稳定阶段的测量值与ANSYS仿真结果对比表明：将有限元运用于真空炉瞬态温度场分析，相对误差在2.536%～3.696%之间，仿真结果与实验测试结果基本一致。运用ANSYS有限元对真空炉反应区域内空间节点模拟计算，可为内热式真空炉分离不同合金时提供炉膛各节点空载下的温度参数。

[1] 张红梅.真空加热区的热场分析[J].电子工业专用设备,2014 (6)：32-36.

[2] 高帆,王新英,王磊,等.TiAl合金真空自耗熔炼过程的数值模拟[J].特种铸造及有色合金,2011 (7):608-611.

[3] 刘静安.镁合金加工技术发展趋势与开发应用前景[J].轻合金加工技术,2001(11):1-7.

[4] 钱中,程惠尔.基于ANSYS的高炉铸钢冷清壁的传热学分析[J].钢铁钒钛,2005 (3):56-59.

[5] 郭应时,付锐,杨鹏飞,等.鼓式制动器瞬态间温度场数值模拟计算[J].长安大学学报(自然科学版), 2006(3):88-90.

[6] 周厚军,杨斌,戴永年,等.氧化铝真空炭热还原炉瞬态温度场模拟计算[J].真空科学与技术学报,2012 (10) :896-901.

[7] 冯丽辉等.内热式多级连续真空炉动态数学模型线性化与仿真[J].中国有色金属学报,1995 (2) :38-41.

[8] 戴永年,杨斌.有色金属真空冶金[M].北京:冶金工业出版社,2009：45-162.

[9] 杨振,余欢.真空度对液态AZ91D镁合金氧化燃烧及蒸发行为的影响[J].特种铸造及有色合金,2013 (3):276-279.

[10] 孔祥谦.有限单元法在传热学中的应用[M].北京:科学出版社,1998.

[11] Gerogiorgis D I,Ydsite B E.AFinite Element CFD Sensitivity Analysis for the Conceptual Design of a Crepeau[A].Warrendale,PA:TMS,2003:407-414.

[12] Winkler O,Bakish R.Vacuum Metallurgy [M].Amsterdam:Elsevier Publishing Company,1971:161-162.

ApplicationofANSYSintemperaturefieldmodelingofvacuumfurnace

WANG Yue-fei, FENG Zhi-qiang, ZHANG Yuan-yuan, LEI Jin-hui, HUANG Yi-jun

As the main equipment of vacuum distillation, vacuum furnace is widely used in the secondary resource regeneration, the extraction of precious metals from binary alloy and the development of new materials. Compared with the traditional pyro-refining method, the vacuum distillation method has the advantages of simple procedure, high direct recovery and no environment pollution. In the actual production, because of the low control level of vacuum furnace temperature, it is very difficult to measure the temperature in the furnace. Therefore, it is significant to carry out the modeling simulation on temperature field. This paper adopts ANSYS to develop simulation calculation on the main coordinate points of internal-heating vacuum furnace. At the same time, a cluster of double platinum-rhodium thermocouple is adopted for test. The results show that the finite element method is applied to analysis of transient temperature field in vacuum furnace, the relative error is 2.536%-3.696%. The simulation results are basically consistent with the test results. This study provides a new method for the analysis of the temperature field of different alloys smelting.

modeling; temperature field; finite element method; ANSYS software; vacuum furnace

TF806.9

B

1672-6103(2017)06-0039-05

广西高校中青年教师基础能力提升项目(KY2016LX437)； 广西高校临海机械装备设计制造及控制重点实验室(GXLH2016YB-02)； 钦州市船舶先进设计制造重点实验室(2016MADMB05)。

王跃飞(1986—)，男，山西人，硕士，讲师，钦州学院任教。

2017-03-20

2017-11-06