不同基线长度的GPS共视授时算法

王彦辉，秘金钟，谷守周

(1．辽宁工程技术大学 测绘与地理科学学院，辽宁 阜新 123000；2．中国测绘学研究院，北京 100830)

不同基线长度的GPS共视授时算法

王彦辉1，2，秘金钟2，谷守周2

(1．辽宁工程技术大学 测绘与地理科学学院，辽宁 阜新 123000；2．中国测绘学研究院，北京 100830)

为了实现不同基线长度的GPS共视授时，研究利用GPS共视授时算法，加入地球自转改正、相对论改正、电离层改正、对流层改正、卫星天线相位中心改正、接收机天线相位中心改正等误差改正来实现算法。实验结果表明：当2个观测站间的基线长度在3 000、2 000、1 000和100 km以内时，共视授时精度可以分别达到4、 3、2和1 ns。

GPS；共视；授时；授时精度；超长基线

0 引言

随着科学技术的高速发展，高精度时间频率传递在通信系统、国防系统和电力系统等领域中的地位日益重要。近年来，我国在国防以及空间技术等方面发展迅速，因而对时间传递精度提出了更高的要求。如同步数字体系(synchronous digital hierarchy，SDH)通信网的时间系统、导弹拦截系统等，要求时间同步精度达纳秒量级。现实中不但需要高精度的时间同步，而且很多部门还要求时间同步的实时性。全球定位系统(global positioning system，GPS)共视时间传递技术具有设备成本低、精度高、操作方便等优点，因此开展GPS共视应用研究对于解决我国的通信系统、国防系统和电力系统等行业对高精度时间同步的需求具有重要意义。

自从利用GPS 码伪距进行时间传递的理念出现以后，授时技术在国外得到了快速的发展：文献[1]总结了GPS授时方法以及相关误差；文献[2]对利用GPS载波进行共视时间传递做了详细阐述；文献[3]分析了不同类型接收机优缺点。同时国内的专家学者在GPS共视授时方面做了大量的探索和研究：文献[4]阐述了一种更为廉价实用的近实时GPS共视方法；文献[5]分析了电离层延迟、对流层延迟等对共视精度的影响；文献[6]对GPS共视技术中的不确定度做了大量研究；文献[7]分析了中国计量科学研究院(National Institute of Metrology，NIM)时间多通道接收机原理；文献[8]对卫星导航系统时间同步中的相关误差做了详细分析；文献[9]分析了卫星共视法原理，并提出了一种新的单向授时法；文献[10]提出了广域空基伪卫星网络的动态传递共视授时方法；文献[11]提出了利用莱特准则进行数据处理，有效解决了由模型所带来残差的问题，并且减轻了由数据处理带来的系统负担。

到目前为止，GPS共视法授时精度已达到纳米级，国际计量局(International Bureau of Weight and Measures，BIPM)已将共视法作为全球 70 多个守时实验室之间时间比对的主要手段之一。现有的有关GPS共视法授时研究大部分只分析了基线长度在1 000 km以内时的共视精度，并未对超长基线做统计分析。本文研究分析基线长度为100 km和1 000 km的GPS共视法授时精度，并且对2 000和3 000 km超长基线的GPS共视法授时进行解算、比对和剖析。

1 GPS共视原理

GPS共视法(common view，CV)是基于 GPS 系统卫星进行的时间同步方法，基本原理是位于不同地点的2个或2个以上观测站同时观测同一颗 GPS 卫星，计算对应观测时刻卫星与测站接收机间的时差，并通过进行实时或事后数据交换而得到2观测站之间相应时刻的时差[12]。2站相距越远，共视的卫星数目越少，则2站获得的共视卫星的观测数据质量越差[9]，2站间共视精度也越低。

1.1 观测方程

A、B2观测站同时观测同一颗卫星，其伪距观测方程[9]为：

(1)

(2)

将式(1)与式(2)相减，得到AB2站间的共视结果为

(3)

由式(3)可以看出：共视可以完全抵消星钟误差，并抵消大部分的星历误差。当2测站相距1 000 km以内时，共视可以抵消单向授时中 95 %以上的星历误差。此外，共视还可以部分抵消电离层延迟误差和对流层延迟误差[13-14]。

1.2 主要误差及其改正

在GPS共视当中会有很多误差影响共视精度，主要分为与卫星相关误差、与测站相关误差、与传播路径相关误差和多路径误差。其中一部分可以利用模型削弱其对GPS共视精度的影响，涉及到的主要误差改正如表1所示。

表1 主要改正误差

2 实验与结果分析

为了实现不同基线长度GPS共视精度比对，选择了4组不同基线长度的MGEX测站数据进行了解算、统计和分析，所用测站信息如表2所示。

表2 测站信息

德国地球科学中心(Deutsches GeoForschungsZentrum，GFZ)的钟差文件(gbm18486.clk gbm18501.clk)中的钟差值精度均达到0.1 ns以上；所以以其钟差为真值，验证不同基线长度下的GPS共视精度。为了更为直观地观察每颗卫星每个历元的不同基线长度下的GPS共视情况，利用2015年年积日第164天至第173天的MGEX数据，分别进行以下实验分析：

1)利用4条不同长度基线对应的每天的观测数据对其做GPS共视处理，得到每颗卫星的共视结果，将此结果减去对应GFZ的钟差值，作为其每个历元的共视精度；

2)对于每条基线每天的GPS共视精度，剔除其大于3倍中误差部分，再统计其标准差，作为每颗卫星的共视精度；

3)将单条基线单天的每颗卫星的GPS共视精度求平均值，作为每条基线的单天共视精度；

4)统计第164天至第173天每天每条基线的共视精度，以及对应的单基线10 d的平均共视精度。

2.1 单星精度统计

为了更为直观地观察单颗卫星每个历元的GPS共视情况，抽取了2015年年积日第165天的共视结果，分别展示4条不同长度基线的GPS第10号卫星和第20卫星的单星共视精度，其精度如图1～图4所示(MYVA-HOFN(173)表示MYVA-HOFN基线，基线长度为173 km)。

图1 MYVA-HOFN(173 km)2015年第165天单星共视精度

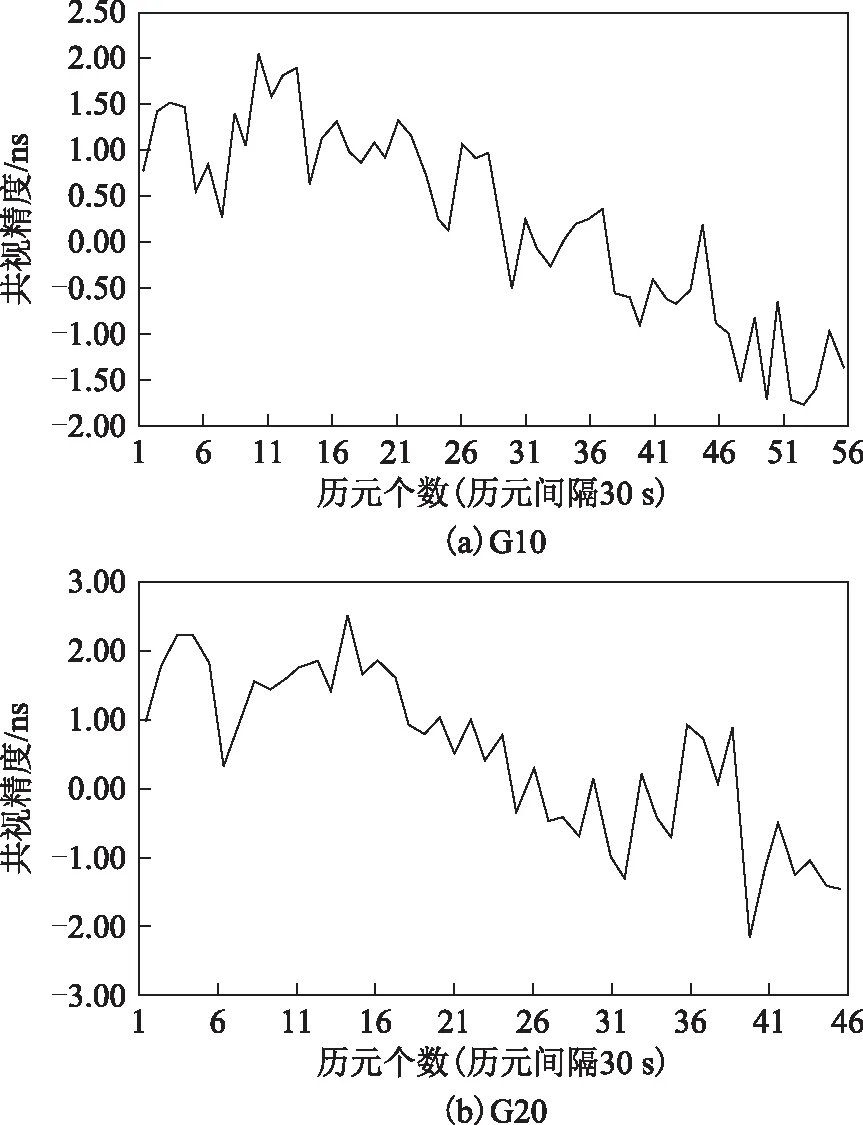
图2 PADO-BRUX(820 km)2015年第165天单星共视精度

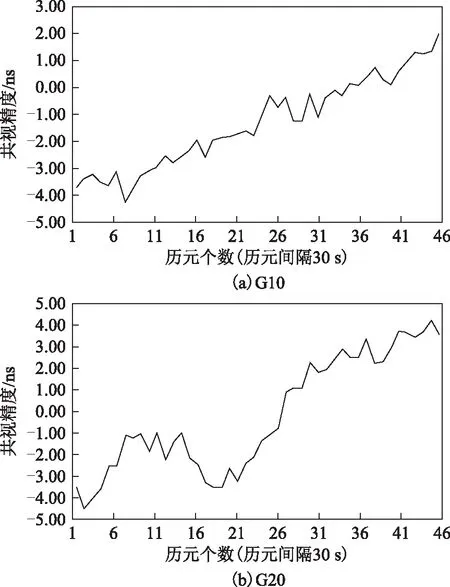
图3 PADO-NICO(2 135 km)2015年第165天单星共视精度

图4 PADO-REYK(2 924 km)2015年第165天单星共视精度

由图1可以看出，当2站间基线长度为173 km(MYVA-HOFN)时，GPS单星共视精度基本在1 ns以内；图2展示的是基线长度为820 km(PADO-BRUX)时的单星共视精度，可以看出其GPS单星共视精度在2 ns以内；图3显示，当2站间基线长度为2 135 km(PADO-NICO)时，2站GPS单星共视精度基本达到了3 ns；图4为当2站间基线长度为2 924 km(PADO-REYK)时，2站GPS单星共视精度大部分在4 ns以内。

2.2 单天精度统计

在剔除大于3倍中误差结果的条件下，以2015年年积日第165天的GPS共视处理结果为例，列举了4条不同长度基线单天共视精度，其精度如图5～图8所示。

图5 MYVA-HOFN(173 km)第165天精度

图6 PADO-BRUX(820 km)第 165天精度

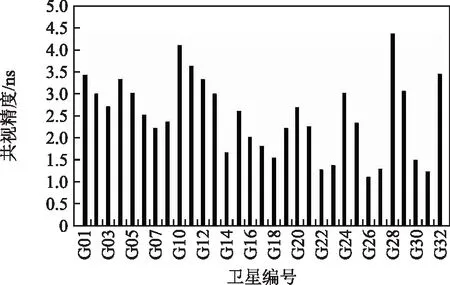
图7 PADO-NICO(2 135 km)第165天精度

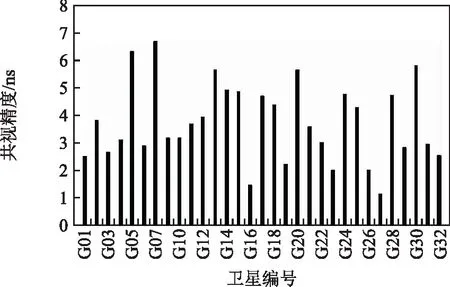
图8 PADO-REYK(2 924 km)第165天精度

从图5可以看出当基线长度为173 km时，2站间的平均GPS共视精度在1 ns左右；图6显示，基线PADO-BRUX(820 km)每颗卫星的GPS共视精度大部分在2 ns以内；观察图7，不难得出当基线长度为2 135 km时，每颗卫星的平均GPS共视精度小于3 ns；由图8可以得出，基线PADO-REYK(2 924 km)单天的平均GPS共视精度满足在4 ns以内。

2.3 多天精度统计

为了使结果更具有普遍性，统计了2015年年积日第164天至第173天共10 d的GPS共视精度，4条不同长度基线的精度统计结果如表3所示。

从表3可知，在这10 d中，4条基线的GPS共视精度无太大的跳变。随着基线长度的增加，电离层和对流层对GPS共视精度的影响逐渐增加；因此基线长度越长，共视精度越低。

2.4 基线精度统计

统计了4条基线2015年年积日第164天至第173天的平均GPS共视授时精度，每条基线的共视精度如表4所示。

从表中可以看出：基线MYVA-HOFN(173 km)平均GPS共视精度为0.984 ns；基线PADO-BRUX(820 km)平均GPS共视精度为1.002 ns；基线PADO-NICO(2 135 km)平均GPS共视精度为2.366 ns；基线PADO-REYK(2 924 km)平均GPS共视精度为3.667 ns。

表3 第164天至第173天精度统计表 ns

表4 第164天至第173天平均精度统计表 ns

由此可以得出以下结论：当基线长度小于100 km时，2观测站间平均GPS共视精度小于1 ns；当基线长度在100和1 000 km之间时，2站间平均GPS共视精度小于2 ns；当2站间距大于1 000小于2 000 km时，其平均GPS共视精度小于3 ns；当2站间基线长度在2 000和3 000 km之间时，其GPS共视精度在4 ns以内。

3 结束语

本文实现了不同基线长度的GPS共视授时，利用MEGX测站数据统计、分析了2015年年积日第164天至第173天10 d中4对测站的GPS共视授时结果。不但给出了基线MYVA-HOFN(173 km)以及PADO-BRUX(820 km)的共视精度，而且分析了超长基线PADO-NICO(2 135 km)和PADO-REYK(2 924 km)的共视精度。分别列举每条基线的单星、单天和多天的GPS共视精度，最后得出，当2站间距在3 000、2 000、1 000和100 km以内时，其共视授时精度分别为4、3、2和1 ns。

[1] ALLAN D W，WEISS M A.Accurate time and frequency transfer during common-view of a GPS satellite[EB/OL].(2001-10-04)[2017-02-18].http：//tf.nist.gov/general/pdf/192.pdf.

[2] DACH R，EUTLER G，HUGENTOBLER U.Time transfer using GPS carrier phase：error propagation and results[J].Journal of Geodesy，2003，77(1)：1-14.

[3] DEFRAIGNE P，BANERJEE P，LEWANDOWSKI W.Time transfer through GPS[EB/OL].(2009-01-29)[2017-02-18].http：//nopr.niscair.res.in/bitstream/123456789/2881/1/IJRSP%2036%284%29%20303-312.pdf.

[4] 杨旭海.GPS共视时间频率传递应用研究[D].西安：中国科学院研究生院，2003：37-57.

[5] 许国宏，韦金辰，陈国宇.双星系统高精度共视授时技术[J].应用科技，2007，34(2)：41-44.

[6] 张鑫，韩小余，应洪伟.GPS共视技术中不确定度分析[J].宇航计测技术，2008，25(5)：31-33.

[7] 高小珣，高源，张越，等.GPS共视法远距离时间频率传递技术研究[J].计量学报，2008，29(1)：80-83.

[8] 刘魁星，桑怀胜，王茂磊，等.卫星导航系统时间同步方法分析与研究[J].电视技术，2010，34(增刊1)：132-133，149.

[9] 许龙霞.基于共视原理的卫星授时方法[D].北京：中国科学院研究生院，2012：7-8，15-25.

[10] 史海清.北斗伪卫星空基增强网络优化与高精度动态时间同步[J].兵工自动化，2014(6)，43-47，57.

[11] 温会锋，张增强.基于3σ法的卫星共视时间传递算法设计[J].航空计算技术，2016，46(5)：98-100.

[12] 王天.北斗卫星导航系统授时性能评估研究[D].西安：长安大学，2014：15-20.

[13] 王正明.GPS共视资料的处理和分析[J].天文学报，2001，42(2)：184-191.

[14] 孙宏伟，李岚，苏哲斌.卫星位置误差对GPS共视时间比对的影响[J].武汉大学学报(信息科学版)，2009，34(8)：968-970.

[15] 李征航，黄劲松.GPS测量与数据处理[M].武汉：武汉大学出版社，2011：120.

AlgorithmofGPScommon-viewtimingondifferentbaselinelengths

WANGYanhui1，2，BEIJinzhong2，GUShouzhou2

(1．School of Geomatics，Liaoning Technical University，Fuxin，Liaoning 123000，China；2．Chinese Academy of Surveying and Mapping，Beijing 100830，China)

In order to realize GPS common-view timing of different baseline lenths，the paper used the GPS common-view timing algorithm with corrections of earth’s rotation correction，the relativistic correction，the ionospheric correction，the tropospheric correction，the satellite antenna phase center correction and the receiver antenna phase center correction to study on the timing on different baseline lengths.Experimental result showed that when the baseline lengths of two observation stations were within 3 000，2 000，1 000 and 100 km，the accuracy of the common-view timing could be 4，3，2 and 1 ns.

GPS；common-view；timing；timing accuracy；very long baseline

2017-02-13

国家重点研发计划课题(2016YFB0501801，2016YFB0502105，2016YFB0501405)；国家自然科学基金项目(41404034，41474011)；全球连续监测评估系统项目(GFZX0301040308-06)；国家863计划项目(2015AA124001)；国家基础测绘科技项目(2016KJ0205)；测绘行业公益性专项(B1503)；中国测绘科学研究院基本科研业务费支持项目(7771604)。

王彦辉(1984—)，男，河北秦皇岛人，硕士研究生，研究方向为精密单点定位与授时。

王彦辉，秘金钟，谷守周.不同基线长度的GPS共视授时算法[J].导航定位学报，2017，5(4)：41-45.(WANG Yanhui，BEI Jinzhong，GU Shouzhou.Algorithm of GPS common-view timing on different baseline lengths[J].Journal of Navigation and Positioning，2017，5(4)：41-45.)

10.16547/j.cnki.10-1096.20170409

P228.1

A

2095-4999(2017)04-0041-05