SR-CDKF在组合导航直接法滤波中的应用

逯 峤,马国梁,张 平,葛敬飞

(1.南京理工大学 能源与动力工程学院,江苏 南京 210094;2.中国人民解放军63863部队,吉林 白城137001;3.中国人民解放军65156部队,辽宁 凌源 122521)

SR-CDKF在组合导航直接法滤波中的应用

逯 峤1,马国梁1,张 平2,葛敬飞3

(1.南京理工大学 能源与动力工程学院,江苏 南京 210094;2.中国人民解放军63863部队,吉林 白城137001;3.中国人民解放军65156部队,辽宁 凌源 122521)

为了解决SINS/GPS组合导航系统姿态、速度和位置等导航参数的非线性估计问题，提出了一种基于平方根中心差分卡尔曼滤波(SR-CDKF)的直接式滤波估计方法。系统状态方程选取惯导力学编排方程,系统状态向量和观测向量分别选取SINS导航参数和GPS输出参数,构建了SR-CDKF滤波器。该滤波器可以使导航参数动态过程得到直接反映,并使得直接式滤波计算流程得以实现。以MATLAB中areoblk_HL20模块为基础构建了仿真系统并进行了仿真。仿真结果表明,该算法具有较高的滤波精度、良好的滤波收敛性和稳定性,能使非线性模型下SINS/GPS组合导航系统的导航要求得到满足。

组合导航;中心差分;卡尔曼滤波;直接校正

SINS/GPS组合导航系统是目前一种比较理想且应用广泛的导航系统。组合导航系统信息处理方法有很多种,Kalman滤波及其扩展方法是目前应用比较广泛的一种方法[1]。根据所选取的被估计系统状态不同,估计方法分为以导航参数为状态变量的直接法和以导航参数误差量为状态变量的间接法2种[2]。如果采用直接估计法,导航参数的动态变化过程可以被系统方程直接而准确地描述,在解算导航参数的同时又进行了滤波估计计算,比间接法简化了计算。

毫无疑问,实际的SINS/GPS组合导航系统的数学模型是非线性方程,而扩展卡尔曼滤波(EKF)是解决非线性系统估计问题应用最多的一种方法。EKF的主要思路是采用Taylor展开将非线性方程线性化后再用标准Kalman滤波作处理,因此EKF的估计误差会随系统非线性程度增强而加大,甚至有时会导致计算发散[3-4],另外EKF需要求Jacobian矩阵,过程繁琐且易出错。

针对EKF的这些不足,由于一个高斯分布的逼近比一个非线性函数的逼近更容易,人们提出了Sigma-point卡尔曼滤波(SPKF)[5]。SPKF主要包括中心差分卡尔曼滤波(CDKF)和无迹卡尔曼滤波(UKF)。其中,CDKF的理论精度比UKF稍高,避开了复杂的Jacobian矩阵计算,更易于实现[6-8]。SR-CDKF不仅继承了CDKF的优点,而且通过直接更新状态变量协方差矩阵的平方根来进行滤波,计算量有所减少,提高了数值计算的稳定性[9-12],因此本文提出将SR-CDKF方法应用到SINS/GPS组合导航系统的导航参数估计中。

1 SR-CDKF算法原理及步骤

1.1 SR-CDKF原理

SR-CDKF的理论基础是中心差分变换,中心差分变换根据数学中的插值理论来对非线性函数进行近似,将Taylor级数展开式中的一阶和二阶导数用中心差分来取代,非线性方程的导数用基于Sterling插值公式的多项式逼近,由此来解决解析微分运算问题[13]。

1.2 SR-CDKF滤波步骤

设状态方程和量测方程具有一般形式:

xk=F(xk-1,uk-1,vk-1)

yk=H(xk,nk)

式中:xk为状态变量,uk为系统输入参数,vk和nk是期望为0且互不相关的高斯白噪声,它们的协方差阵分别为Rv和Rn,即有:

设xk,vk和nk的维数分别为Lx、Lv和Ln,则执行SR-CDKF滤波计算的步骤如下[14]。

①确定滤波初值。

当k=0时,滤波初值为

式中:chol{*}表示对矩阵进行cholesky分解。

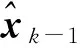
②计算时间更新所需要的sigma点集。

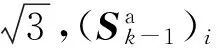
③确定权值。

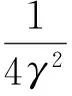
④时间更新。

式中:qr(A)表示对矩阵A进行QR分解后得到的R矩阵下三角部分。

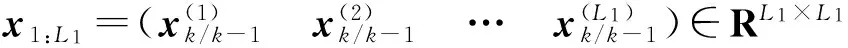
⑤计算量测更新所需要的sigma点。

⑥量测更新。

式中:

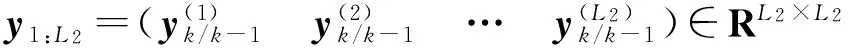
⑦计算增益和更新状态。

式中:cholupdate{*}表示矩阵的cholesky更新。

2 SINS/GPS组合导航非线性模型

2.1 直接式SINS/GPS组合导航系统滤波器结构

在直接式SINS/GPS组合导航滤波器中[15],首先由惯性器件和GPS分别测量运载体的运动状态,其次SR-CDKF滤波器接受惯性器件测得的角速率、比力和GPS测得的位置速度信息,经SR-CDKF滤波器处理计算后输出组合导航系统的导航参数最优估计值,如图1所示。

2.2 组合系统状态方程

本文根据文献[16],捷联惯导系统(SINS)导航坐标系(n系)选用“北东地”地理坐标系建立的非线性姿态、速度和位置方程如下。

姿态方程为

(1)

(2)

陀螺仪测量值模型为

(3)

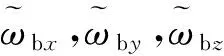
速度方程为

(4)

加速度计的测量模型为

(5)

位置方程为

(6)

式中:RN和RM分别为参考椭球卯酉圈和子午圈曲率半径;L,λ,h分别为载体所在的纬度、经度和高度。

④关于陀螺常值漂移ε和加速度计零偏Δ,本文中用随机常数来表示:

(7)

以式(1)～式(7)为状态,选取组合导航系统方程状态变量x(t)为

x(t)=(φθψvNvEvDLλh
εxεyεzΔxΔyΔz)T

因此,系统状态方程可以表示为

2.3 观测方程

量测值y取GPS输出的速度参数和位置参数,即y=(vN,GPSvE,GPSvD,GPSLGPSλGPShGPS)T,基于前面所选取的系统方程状态变量x和量测值y,观测方程可写成

yk=H(xk,nk)=HPVxk+nk

式中:HPV=(O6×3I6×3O6×6),yk和xk分别为y和x在k时刻的值,nk=(nvNnvEnvDnLnλnh)T为测量噪声。

3 仿真分析

1)真值的生成。

为了对SR-CDKF滤波算法作进一步分析,本文采用MATLAB中aeroblk_HL20模块中的子模块6DOF(Euler Angles)产生的数据作为原始数据。由于该模块输出的运动参数均是在忽略地球自转和地球曲率的假设下得出的,因此如果采用这些数据作为参考真值,需要将前述的惯性导航方程(即系统状态方程)简化,方程的非线性也会减弱,体现不出SR-CDKF方法相对于其他非线性滤波方法的优势。另外,简化的导航方程由于忽略了地球曲率,因此只适合于短距离导航,而完整的导航方程无此限制,拓宽了参考真值的数据适用范围。综上所述,需要将原始数据进行转化,以得到完整的惯性导航方程下的运载体真实的运动参数,具体的转换思路和方法参见文献[16]。

2)仿真初始条件。

设定SINS和GPS的采样周期分别为0.01 s和0.1 s,仿真时间70 s,设置仿真初始条件:初始滚转角、俯仰角、偏航角误差分别为3°,3°和5°;初始经度、纬度、高度误差为10 m,10 m和20 m;初始北向、东向、地向速度误差均为0.3 m/s。陀螺仪三轴白噪声均方差均为0.1°/s;三轴常值漂移分别为-0.1 °/s,0.1 °/s和-0.1 °/s;加速计白噪声均方差均为0.05 m/s2;三轴零偏分别为-0.01 m/s2,0.01 m/s2和-0.02 m/s2;GPS位置和速度精度分别取5 m和0.1 m/s,初始协方差矩阵P为对角阵,除了对角线元素,其他元素均为0,其对角线元素为

P(1,1)=P(2,2)=P(3,3)=52
P(4,4)=P(5,5)=P(6,6)=0.32
P(7,7)=P(8,8)=P(9,9)=102
P(10,10)=P(11,11)=P(11,12)=0.22
P(13,13)=P(14,14)=P(15,15)=0.32

3)仿真结果。

在前文给出的仿真条件下,由于UKF、CDKF仿真曲线与SR-CDKF仿真曲线比较接近,在同一幅图中会相互重叠,不能明显看出优劣,因此只给出了SINS/GPS组合导航系统基于SR-CDKF的滤波仿真曲线,如图2～图6所示。

从图2～图6可看出,组合导航系统的运载体姿态角参数在10 s左右就收敛了,速度和位置参数则收敛得更快,陀螺和加速度计零偏基本都在20 s内收敛,且各参数的计算均未发散,表明计算稳定,从一定程度上验证了SR-CDKF方法的数值稳定性。从图中还可看出,在有测量噪声和固定零偏的情况下,各导航参数(姿态、速度、位置等)上下波动范围较小,表明滤波计算的误差比较小。

在仿真条件下,UKF、CDKF和SR-CDKF 3种估计方法得到的运动参数估计误差均方差如表1～表5所示。

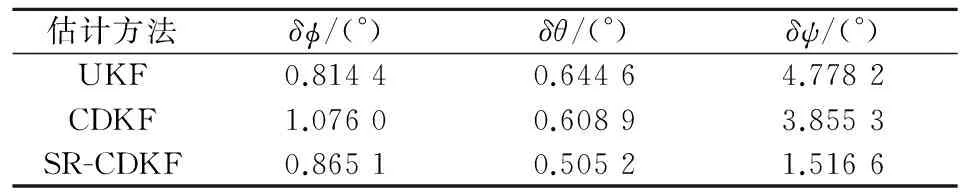
表1 姿态角估计误差标准差比较

表2 速度估计误差标准差比较

表3 位置估计误差标准差比较

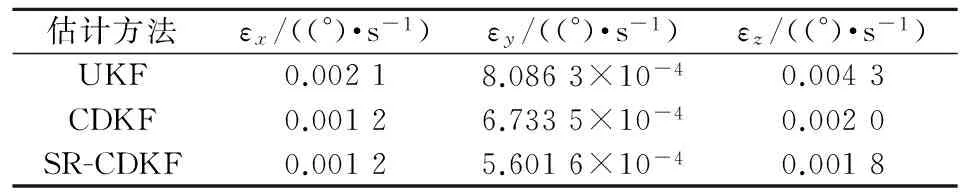
表4 陀螺仪漂移估计值标准差比较

表5 加速度计零偏估计值标准差比较

由误差数据表1～表5看出,CDKF比UKF估计误差标准差要小,精度稍微好一些,验证了CDKF理论精度稍高于UKF这一事实。而总体上看SR-CDKF对各个运动参数的估计误差的标准差均小于UKF和CDKF,即估计精度均高于CDKF和UKF,同时也表明SR-CDKF的数值稳定性好于UKF和CDKF。综上,SR-CDKF能提高非线性系统的滤波精度,使复杂的非线性系统滤波估计问题得以有效解决,同时使组合导航系统具有较高的导航精度。

4 结论

本文采用平方根中心差分卡尔曼滤波方法,研究了直接式的SINS/GPS组合导航估计问题,分别以姿态、速度、位置和零偏等导航参数和GPS的速度和位置为系统状态向量和观测向量,将惯导力学编排方程作为系统状态方程,以MATLAB中aeroblk_HL20模块产生的数据经过适当转换后作为仿真的参考真值,并在此基础上生成SINS和GPS的测量值,经滤波器估计后得到系统输出,即导航参数的最优估计值。仿真结果表明,SR-CDKF可以较好地处理非线性模型的滤波问题,摆脱了传统的对非线性方程进行Taylor展开的线性化过程,计算量较小,且能保证滤波过程的数值稳定,简化了滤波过程,使系统导航精度得到了提高。

[1] 付心如,徐爱功,孙伟.抗差自适应UKF的INS/GNSS组合导航算法[J].导航定位学报,2017,5(2):111-116.

FU Xin-ru,XU Ai-gong,SUN Wei.An INS/GNSS integrated navigation algorithm based on robust adaptive UKF[J].Journal of Navigation and Positioning,2017,5(2):111-116.(in Chinese)

[2] 孟阳,高社生,高兵兵,等.基于UKF的INS/GNSS/CNS组合导航最优数据融合方法[J].中国惯性技术学报,2016,24(6):746-751.

MENG Yang,GAO She-sheng,GAO Bing-bing,et al.UKF-based optimal data fusion method for integrated INS/GNSS/CNS[J].Journal of Chinese Inertial Technology,2016,24(6):746-751.(in Chinese)

[3] 袁赣南,赵自超,贾鹤鸣,等.CDKF算法在四旋翼飞行器组合导航系统中应用[J].吉林大学学报(信息科学版),2015,33(2):161-167.

YUAN Gan-nan,ZHAO Zi-chao,JIA He-ming,et al.CDKF algorithm applied to quadrotor integrated navigation system[J].Journal of Jilin University(Information Science Edition),2015,33(2):161-167.(in Chinese)

[4] 潘加亮,熊智,王丽娜,等.一种简化的发射系下SINS/GPS/CNS组合导航系统无迹卡尔曼滤波算法[J].兵工学报,2015,36(3):484-491.

PAN Jia-liang,XIONG Zhi,WANG Li-na,et al.A simplified UKF algorithm for SINS/GPS/CNS integrated navigation system in launch inertial coordinate system[J].Acta Armamentarii,2015,36(3):484-491.(in Chinese)

[5] JULIER S,UHLMANN J,DURRANT-WHYTE H F.A new method for the nonlinear transformation of means and covariances in filters and estimators[J].IEEE Transactions on Automatic Control,2000,45(3):477-482.

[6] 贾鹤鸣,杨泽文,宋文龙.基于中心差分卡尔曼滤波的初始对准方法研究[J].森林工程,2016,32(6):66-70.

JIA He-ming,YANG Ze-wen,SONG Wen-long.Study on initial alignment method based on central difference Calman filter[J].Forest Engineering,2016,32(6):66-70.(in Chinese)

[7] 张召友,郝燕玲,吴旭.3种确定性采样非线性滤波算法的复杂度分析[J].哈尔滨工业大学学报,2013,45(12):111-115.

ZHANG Zhao-you,HAO Yang-ling,WU Xu.Complexity analysis of three deterministic sampling nonlinear filtering algorithms[J].Journal of Harbin Institute of Technology,2013,45(12):111-115.(in Chinese)

[8] 韩萍,干浩亮,何炜琨,等.基于迭代中心差分卡尔曼滤波的飞机姿态估计[J].仪器仪表学报,2015,36(1):187-193.

HAN Ping,GAN Hao-liang,HE Wei-kun,et al.Iterated central difference Kalman filter based aircraft attitude estimation[J].Chinese Journal of Scientific Instrument,2015,36(1):187-193.(in Chinese)

[9] 陈晓威,张国毅,李彦志,等.基于SRCDKF的相位差变化率无源定位算法[J].电子信息对抗技术,2016,31(1):8-11.

CHEN Xiao-wei,ZHANG Guo-yi,LI Yan-zhi,et al.Passive location algorithm of phase difference rate of change based on SRCDKF[J].Electronic Warfare Technology,2016,31(1):8-11.(in Chinese)

[10] 贾鹤鸣,宋文龙,牟宏伟,等.ISR-CDKF在SINS大方位失准角初始对准中的应用[J].吉林大学学报(信息科学版),2013,31(2):196-202.

JIA He-ming,SONG Wen-long,MOU Hong-wei,et al.Application of ISR-CDKF in initial alignment of large azimuth misalignment in the SINS[J].Journal of Jilin University(Information Science Edition),2013,31(02):196-202.

[11] DUAN J,LIU D,YU H,et al.An improved fast SLAM algorithm for autonomous vehicle based on the strong tracking square root central difference Kalman filter[C]//2015 IEEE 18th International Conference on Intelligent Transportation Systems(ITSC).Spain:IEEE,2015:693-698.

[12] TANG X,YAN J,ZHONG D.Square-root sigma-point Kalman filtering for spacecraft relative navigation[J].Acta Astronautica,2010,66(5-6):704-713.

[13] 郝燕玲,牟宏伟.自适应平方根中心差分卡尔曼滤波算法在捷联惯性导航系统大方位失准角初始对准中的应用[J].吉林大学学报(工学版),2013,43(1):261-266.

HAO Yang-ling,MOU Hong-wei.Application of adaptive SRCDKF in SINS initial alignment with large azimuth misalignment[J].Journal of Jilin University(Engineering and Technology Edition),2013,43(1):261-266.(in Chinese)

[14] HAO Y L,YANG J W,CHEN L,et al.Initial alignment of large azimuth misalignment based on square root central difference Kalman filter[J].Journal of Chinese Inertial Technology,2011,19(2):180-184.

[15] 王林,林雪原.基于UKF的GPS/SINS组合导航直接式滤波算法[J].导航定位与授时,2015(3):43-48.

WANG Lin,LIN Xue-yuan.Direct Kalman filtering algorithm for the GPS/SINS integrated navigation based on UKF[J].Navigation Positioning and Timing,2015(3):43-48.(in Chinese)

[16] 刘可可.基于Kalman滤波的滚转弹运动参数GPS/IMU组合测量方法研究[D].南京:南京理工大学,2016.

LIU Ke-ke.Research on GPS/IMU integrated measurement method of spinning projectile motion parameters based on Kalman filter[D].Nanjing:Nanjing University of Science and Technology,2016.(in Chinese)

ApplicationofSR-CDKFinDirectFilteringofIntegratedNavigation

LU Qiao1,MA Guo-liang1,ZHANG Ping2,GE Jing-fei3

(1.School of Energy and Power Engineering,Nanjing University of Science and Technology,Nanjing 210094,China;2.Unit 63863 of PLA,Baicheng 137001,China;3.Unit 65156 of PLA,Lingyuan 122521,China)

In order to solve the nonlinear estimation problem of the navigation-parameters about SINS/GPS integrated navigation system such as attitudes,speeds and positions,a direct filtering estimation method was proposed based on Square Root Center Differential Kalman Filter(SR-CDKF).The system state vectors and observation vectors respectively consisted of SINS navigation-parameters and GPS output parameters,and the SR-CDKF filter was constructed.The filter can directly reflect the dynamic process of navigation parameters and realize the direct filtering calculation-process.Based on the areoblk_HL20 module in the MATLAB,the simulation system was built,and the simulation was carried out.The simulation results show that the algorithm has high filtering-accuracy,good convergence and stability of filtering,and the navigation requirements of SINS/GPS integrated navigation system under the condition of the nonlinear model can be satisfied.

integrated navigation;central difference;Kalman filter;direct correction

TP273

A

1004-499X(2017)04-0029-06

2017-05-10

逯峤(1990-),男,硕士研究生,研究方向为卡尔曼滤波与组合导航。E-mail:lqnust900605@126.com。

马国梁(1976-),男,副教授,博士,研究方向为导航、制导与控制。E-mail:mgl@njust.edu.cn。