基于LuGre摩擦模型的转台伺服系统自适应摩擦补偿研究

郭远韬，闵 斌，陈 斌

(1.上海航天控制技术研究所,上海 201109； 2.上海航天技术研究院，上海 201109)

基于LuGre摩擦模型的转台伺服系统自适应摩擦补偿研究

郭远韬1，闵 斌2，陈 斌1

(1.上海航天控制技术研究所,上海 201109； 2.上海航天技术研究院，上海 201109)

为消除非线性摩擦对测试转台性能的影响，选用LuGre摩擦模型描述转台系统所受的非线性摩擦。根据转台直流电机系统数学描述，提出了非线性摩擦补偿方法。设计了双观测器结构估计LuGre模型中的不可测状态；考虑LuGre模型中3个参数的非一致性变化，设计了自适应摩擦补偿控制算法，在线估计摩擦模型中的参数，并对非线性摩擦进行补偿。用李雅普诺夫方法证明了采用自适应摩擦补偿方法的闭环系统的稳定性。仿真结果表明：正弦波输入时，摩擦补偿后的位置跟踪误差(峰-峰值)较无摩擦补偿减小了1个量级，位置跟踪性能有较大改善，辨识出的摩擦模型参数能稳定收敛于真实值附近；三角波输入时，自适应控制的位置跟踪精度更高。

测试转台； LuGre摩擦模型； 非线性摩擦； 不可测状态； 双观测器结构； 自适应摩擦补偿； 稳定性； 位置跟踪

0 引言

高精度测试转台是检测和评价惯性导航与制导系统的主要设备，利用高精度测试转台对陀螺仪和加速度计进行研究，建立其数学模型，鉴定其精度等级，通过不同的试验方法确定被测仪表的各种误差因素，可对其进行补偿以提高整个惯导系统的精度。因此，测试转台的优劣直接关系测试试验的可靠性和置信度，是保证航空航天产品和武器系统精度及性能的基础，对航空、航天工业和国防建设有重要意义。摩擦力是影响测试转台精度的一个重要因素，它具非线性，常会导致转台伺服系统出现稳态误差、极限环和低速爬行等问题。为提高转台的精度，须采取合理的摩擦补偿方法降低或消除非线性摩擦对转台伺服系统的影响。摩擦补偿方法有多种，根据其是否需要具体的摩擦模型，可分为非模型的和基于模型的两种。对非模型补偿，可采用传统PID/PD控制器，但不能满足高精度位置跟踪需求，也易造成系统出现极限环振荡，或将摩擦力矩干扰等效为不确定周期扰动，通过设计鲁棒控制器予以克服[1]。此外，还可采用神经网络控制和模糊逻辑控制等摩擦补偿方法[2-3]。基于模型的补偿方法通常是在线估计摩擦模型的参数，将一个摩擦补偿项加入标准的控制算法对摩擦进行补偿[4-6]。基于摩擦模型的补偿方法取决于摩擦模型的选择，摩擦模型越能真实反映摩擦的动静态特性，摩擦的补偿效果就越好。摩擦的数学模型有库伦摩擦模型、Stribeck摩擦模型、Karnopp摩擦模型等多种形式，但上述模型均属于静态模型，不能正确描述摩擦的动态特性，如临界摩擦力、摩擦滞后、预滑动位移和摩擦滞回等现象[7-8]。1968年，DAHL提出了Dahl摩擦模型，通过引入一个内部状态变量，反映摩擦的记忆现象。WIT等在Dahl模型的基础上提出了LuGre摩擦模型，赋予状态变量确切的物理含义，使其模型不但可描述增加的静摩擦力及摩擦记忆现象，而且能描述Stribeck曲线，是目前较完善的一个模型。本文基于LuGre摩擦模型设计自适应摩擦补偿算法，基于LuGre摩擦模型中的状态变量无法直接测得，设计两个状态观测器，观测摩擦模型中的状态变量，辨识出摩擦模型系数并进行补偿。

1 摩擦模型建立

LuGre摩擦模型将产生摩擦的接触面视为有大量随机行为的鬃毛，当有切向作用力时，鬃毛像弹簧般变形产生摩擦力，模型通过鬃毛接触点形成、鬃毛变形、接触点断开，以及新接触点形成的过程描述摩擦的动态行为[9-10]。鬃毛的平均形变可用z表示，有

(1)

(2)

式中：Fc为库伦摩擦力；Fs为最大静摩擦力；ωs为Stribeck速度。则由鬃毛产生的摩擦力加上黏性摩擦，总摩擦力

(3)

式中：σ0，σ1，σ2分别为鬃毛刚性系数、滑动阻尼系数和黏性摩擦因数，这些参数会在外界温度、润滑条件、材料磨损及接触面作用力等因素的影响下发生改变[11-12]。

2 摩擦补偿方法设计

2.1 转台直流电机系统数学描述

在机械轴承转台的位置控制中，通常采用永磁直流力矩电机作为其驱动装置，因其除普通电励磁直流电机具备的调速范围宽和便于控制等特点外，还有体积小、效率高、用铜量少、结构简单和运行可靠等优点。经适当简化，永磁直流力矩电机的传递函数如图1所示。图1中：La为电机电枢电感；Ra为电机电枢电阻；Ki为电机力矩系数；Ke为电机反电势系数；J为电机包括负载在内的转动惯量；Mfric为系统所受摩擦力矩；u为控制输入。

由图1可得微分方程

(4)

(5)

(6)

令a=JRa/Ki，b=-Ke，则式(6)可写为

(7)

转台的控制系统一般由电流环、速度环和位置环构成。电流环和速度环的作用是提高系统的刚度以抑制系统的非线性及外部扰动，控制系统的精度主要由位置环保证。工程实践中常用PID控制器调节位置环的性能，但常规PID控制往往不能消除非线性摩擦对系统的影响，因此需设计控制算法补偿非线性摩擦，提高转台系统的精度。

2.2 非线性摩擦补偿方法设计

因LuGre摩擦模型中的参数σ0，σ1，σ2会受温度和材料磨损等外界因素影响发生变化，故需用自适应控制算法在线辨识出后，再对非线性摩擦进行补偿[9]。

带摩擦的伺服系统微分方程可简化为

(8)

将式(3)中的摩擦模型代入式(8)，可得

(9)

将式(1)代入式(9)，得

(10)

式中：β=σ1+σ2>0。

引入误差项

e=θ-θr

(11)

(12)

式中：λ为大于0的常数；θr为期望位置信号。当ε很小或指数收敛到0时，e也会收敛到0。则可得

(13)

为获得摩擦模型中的z，设计两个闭环观测器为

(14)

(15)

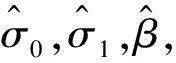
(16)

将控制率式(16)代入式(13)，则有

(17)

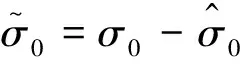
用基于李雅普诺夫函数方法证明上述基于双观测器结构的自适应摩擦补偿方法的闭环稳定性。建立李雅普诺夫函数

(18)

式中：r0，r1，r2为自适应增益，均为大于0的常数，由设计者选取。对式(18)李雅普诺夫函数沿式(13)～(15)微分，可得

(19)

选择参数估计值和观测器补偿项为

(20)

(21)

(22)

τ0=-ε

(23)

(24)

用上述更新率后李雅普诺夫函数的导数

(25)

3 仿真与分析

在Matlab/Simulink仿真环境中对上述自适应摩擦补偿方法进行仿真研究。选择某测试转台的直流力矩电机系统参数和LuGre摩擦模型参数为：a=0.25；b=-2.5；σ0=9.8 N·m/rad；σ1=5.8 N·m·s/rad；β=5.87 N·m·s/rad；Mc=0.12 N·m；M1=0.033 N·m；ω1=0.001 rad/s。分别比较单PID控制率和补偿后的PID控制率。

考虑正弦波输入，给定输入位置信号θr=0.5sin(πt)，取控制增益和自适应增益为λ=300，k=300，r0=2 000，r1=4 000，r2=2 000，无/有自适应控制率的位置跟踪误差结果分别如图2、3所示，有自适应控制率的摩擦参数估计结果如图4所示。

由图2、3可知：加入摩擦补偿后的位置跟踪误差(峰-峰值)较无摩擦补偿减小了1个量级，位置跟踪性能有较大改善。由图4可知：辨识出的摩擦模型参数都稳定收敛于真实值附近。仿真结果表明：当非线性摩擦力模型中参数发生非一致性变化时，用本文的自适应补偿方法能准确辨识出摩擦力参数，并对非线性摩擦进行补偿，明显改善了转台系统的位置跟踪性能。

考虑三角波输入，以周期10 s、速度幅值0.000 5 rad/s的三角波作为输入，比较两种控制方法的位置跟踪误差，所得PID控制器和自适应控制的位置跟踪误差分别如图5、6所示。

由图5、6可知：在三角波输入下，采用PID控制的转台系统位置跟踪误差为1.5×10-5rad(峰-峰值)，采用自适应控制的转台系统位置跟踪误差为6×10-8rad(峰-峰值)，自适应控制的位置跟踪精度更高。

4 结束语

本文分析了转台伺服系统中的非线性摩擦及其对系统的影响。考虑LuGre模型中存在不可测的状态，设计了双观测器结构估计摩擦模型中的不可测状态，再考虑LuGre摩擦模型中的三个参数产生非一致性变化的情况下，用李雅普诺夫稳定性分析方法设计了自适应摩擦补偿控制算法，在线估计出摩擦模型中的参数，并对非线性摩擦进行补偿。仿真结果显示：用本方法可明显改善转台伺服系统的位置跟踪性能，并能动态辨识出摩擦模型参数，证实了本方法的有效性。本方法选用的LuGre模型较其他模型能更真实地反映转台运动过程中的摩擦力，由在线估测使LuGre模型实时更新状态，进一步提高了模型本身的准确度，控制方法对提高转台位置精度指标有实际应用价值。

[1] 王本永. 基于H∞控制理论的液压三轴仿真转台控制系统研究[D]. 哈尔滨: 哈尔滨工业大学, 2008.

[2] SELMIC R R, LEWIS F L. Netural network approximation of piecewise continuous functions: application to friction compensation[J]. IEEE Transactions on Neural Networks, 2002, 13(3): 745-751.

[3] 王永富, 柴天佑. 一种补偿动态摩擦的自适应模糊控制方法[J]. 中国机电工程学报, 2005, 25(2): 139-143.

[4] YAZDIZADEH A, KHORASANI K. Adaptive friction compensation based on the Lyapunov scheme[C]// IEEE International Conference on Control Applications. Dearborn: IEEE, 1996: 1060-1065.

[5] VEDAGARBHA P, MDAWSON D. Tracking Control of mechanical systems in the presence of nonlinear dynamic friction effects[J]. IEEE Transactions on Control Systems Technology, 1999, 7(4): 446-456.

[6] 王忠山. 高精度机械轴承转台摩擦补偿研究[D]. 哈尔滨: 哈尔滨工业大学, 2007.

[7] WIT C D. A new model for control of systems with friction[C]// IEEE Transactions on Automatic Control. Houston: IEEE, 1995: 419-425.

[8] TAN Y, KANELLAKOPOULOS I. Adaptive nonlinear friction compensation with parametric uncertainties[C]// American Control Conference. Washington D. C.: [s. n.], 1999: 2511-2515.

[9] 王瑞娟, 梅志千, 李向国. 机电伺服系统非线性摩擦自适应补偿的研究[J]. 中国电机工程学报, 2012, 32(36): 123-128.

[10] 王英, 熊振华, 丁汉. 基于状态观测的自适应摩擦力补偿的高精度控制[J]. 自然科学进展, 2005, 15(9): 1100-1105.

[11] 周金柱, 段宝岩, 黄进. LuGre摩擦模型对伺服系统的影响与补偿[J]. 控制理论与应用, 2008, 25(6): 990-994.

[12] TAN Y, TAN H. Adaptive backstepping control and friction compensation for AC servo with inertia and load uncertainties[J]. IEEE Transactions on Industrial Electronics, 2003, 50(5): 944-953.

StudyonAdaptiveFrictionCompensationofTurntableServoSystemsBasedonLuGreFrictionModel

GUO Yuan-tao1， MIN Bin2， CHEN Bin1

(1. Shanghai Institute of Spaceflight Control Technology, Shanghai 201109, China;2. Shanghai Academy of Spaceflight Technology, Shanghai 201109, China)

To eliminate the effect of nonlinear friction on test turntable, LuGre friction model was selected to describe nonlinear friction of the test turntable. According to the mathe description of the DC motor system, the method to compensate the nonlinear friction was put forward. The dual-observer was designed to estimate the unmeasurable state in the LuGre friction. Taking into account the occurrence of 3 non-uniform parameters change in LuGre friction model, the control algorithm with adaptive friction compensation was designed, which estimated the parameters in the friction model on line and compensate the nonlinear friction. The system stability of the closed-loop with adaptive friction compensation was proved by Lyapunov approach. The simulation results showed that the position tracking error (peak-peak) with compensation was 1 order smaller than the one without compensation and the performance of the position tracking was improved greatly as well as the estimated parameters of the friction model were converged to around the true value for sinusoidal input. The accuracy of the position tracking with adaptive control was much higher for triangular waveform input.

test turntable; LuGre friction model; nonlinear friction; unmeasurable state; dual-observer; adaptive friction compensation; stability; position tracking

2017-08-19；

2017-10-22

郭远韬(1989—)，男，硕士，主要研究方向为伺服系统摩擦补偿。

1006-1630(2017)06-0065-05

TM921.54

A

10.19328/j.cnki.1006-1630.2017.06.010