沿海摆位航线航次效益测算
2018-01-07董良才
董良才
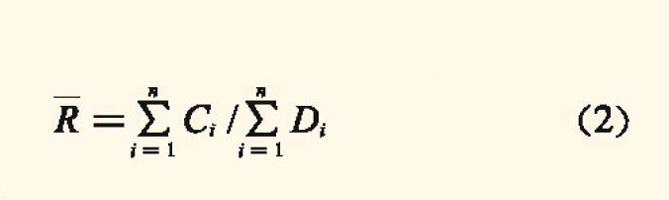

【摘 要】 为优化沿海散货运输摆位航线航次效益测算,评价其摆位航次的价值,运用闭环调整和船位价值理论两种方法对沿海摆位航次的期租水平进行调整。结果表明:闭环调整方法对提供摆位货载、执行摆位航线的部分客户评价具有明显的效用,但对航次营运天进行调整会导致航次效益测算值上下浮动较大;船位价值理论办法的适用性更为广泛,但需要经营者对市场波动趋势进行预判,航次期间不同的市场租金水平会导致调整结果的不同。在实践中,船舶经营者可以根据需要选用其中一种或者两种方法相结合计算摆位航次效益测算,以支持决策需要。
【關键词】 沿海运输;摆位航次;期租水平;闭环调整;船位价值
0 引 言
自2008年以来,国际干散货运输市场持续低迷。上海航运交易所公布的中国沿海散货运价指数(CBCFI)通过细分沿海运输船型、货种、航线等,发布每日沿海散货运价指数,但随着沿海运输业务的发展,航线逐渐出现了超出上海航运交易所公布的指数业务范围,尤其是在矿石航线方面出现了如海南铁矿石运往长江港口或北方港口、福建可门铁矿石运往长江港口,以及湛江铁矿石运往长江港口等相关航线。此类沿海散货运输航线类似于远洋运输航线中好望角型船远东―欧陆、巴拿马型船远东―西欧、灵便型船中国北方―西非等摆位航线,可以称之为沿海摆位航线。沿海散货运价指数中并没有公布此类航线运价相关指数,由此给经营此类航线的内贸船舶所有人在面临航线选择和效益测算方面带来了诸多不便。本文从航次时间和航次燃油成本入手,介绍沿海摆位航次效益测算的两种方法,为沿海船舶经营者提供决策支持。
1 沿海运输航线及航线选择
1.1 沿海运输循环航线和摆位航线
在沿海运输中,通常的标准航线如秦皇岛―广州或秦皇岛―上海的循环航线,其航次形式通常表现为船舶从航次起始港广州港(或上海港)空载至秦皇岛港装载煤炭返回广州港(或上海港)卸货,至船舶离港时该航次结束。以此循环,形成一个完整的循环航线。
广西、福建、海南等地港口有少量铁矿石货源,船舶在广州港空载后可以选择去此类港口装运铁矿石返回长江及北方等地港口,使得船舶下一航次起始点距离秦皇岛港等煤炭装运港更近。该类航线可以称之为沿海摆位航线。
1.2 航次期租水平
航次期租水平R是反映船舶航次经营情况的指标,表示在不考虑船舶固定成本情况下的船舶执行航次的效益水平情况,反映船舶经营者的经营水平。航次期租水平计算式为
R=C/D(1)
式中:C为航次贡献毛利,即航次运输净收入 航次变动成本,万元;D为航次营运天,d。
多个航次的平均期租水平R的计算式为
1.3 航线选择
船舶在广州港空载出发时,有两种航线方案可以选择:方案A,继续执行秦皇岛港装煤的循环航线(航次租金水平为RA);方案B,船舶航行至海南等地港口装载铁矿石后去往镇江港或者其他北方港口的摆位航线(航次租金水平为RB)。
在实际执行中,由于方案B的运价明显低于方案A,RB远远小于RA,但这并不能说明方案B的实际航次效益低于方案A。方案B在执行装载铁矿石航次时,将船舶位置由广州港摆位至镇江港,使得船舶具备一定的船位价值。在方案B之后,船舶可以继续执行镇江―秦皇岛―广州航线的方案C。方案C中船舶具有位置优势,船舶空放距离大大缩小,因而船舶航次效益得到大幅提升。
因此,传统方法往往将方案A的RA与方案B+方案C的平均航次期租水平RB+C进行比较,确定方案A和方案B的效益优劣,以便船舶所有人作出效益最大化的决策。
但是,以上传统方法存在一定的局限性:
(1)假定方案A航次的结束港与方案B+方案C航次后的结束港为相同港口或等价位置,而在实际经营过程中航次卸货港并不一定具备这些条件;
(2)假定内贸市场水平在一段期间(如方案B+方案C航次执行期间)内变化浮动不大,因为方案A的航次营运天少于方案B+方案C的航次总营运天,进而未考虑方案A航次之后的衔接航次可获得的更大收入的机会成本;
(3)时效性较差,该方法可应用于航次结束后进行的后评估,但对即时决策支持作用效果较小。
2 沿海摆位航次效益测算方法
2.1 航次闭环调整
船舶在某个港口Q空出,然后通过一个或者多个航次航线的执行,重新回到港口Q位置的空出状态,可以称之为一个循环航线或者闭环航线。如果将前述方案B或者方案C航次进行虚拟闭环,进而组合成相应的循环航线,能够有效消除船位因素价值。比较闭环后的期租水平与方案A航次的期租水平,能够更快速地得出两种方案效益水平的高低,更有利于决策的时效性需要。
方案A航次为闭环航次,其租金水平计算可以拆分为空载租金水平RA空和重载租金水平RA重。
式中:CA为方案A航次的贡献毛益,美元; DA为方案A航次的总营运天,d; CA空为方案A航次空载部分的贡献毛益,美元; CA重为方案A航次重载部分的贡献毛益,美元; DA空为方案A航次空放部分的总营运天,d; DA重为方案A航次重载部分的总营运天,d。
假设该方案A航次的重载部分单独为一个航次,则其期租水平RA重=CA重 / DA重。
因此,船舶在北方港口如秦皇岛港单装煤炭至广州港卸货的这一航次,即为方案A航次的重载部分航次,由其重载租金水平RA重可以得出其闭环租金水平为RA。
方案B航次的船舶在广州港空出后经某港口装载至秦皇岛港卸货,如该航次租金水平为RB重,则该航次进行闭环调整后的租金水平为RB。
船舶在秦皇岛港卸货后,继续执行秦皇岛港装载至广州港卸货的方案C航次,这样船舶经方案C航次后又回到相同的位置,形成有效闭环,即完成方案B航次的一次闭环航线。方案C航次的租金水平等于方案A航次重载部分的租金水平RA重,那么方案B航次闭环后重载部分的期租水平可表示为
式中:RB为方案B航次闭环后的期租水平,美元/d; CB重为方案B航次重载部分的贡献毛益,美元; DB重为方案B航次重载部分的总营运天,d。
由式(4)可以看出,影响闭环后期租水平的主要因素为船舶空放部分的貢献毛益CA空和空放天DA空。同时,由于船舶空放的收入为零,其空放的贡献毛益实为支付的燃油成本,即:
式中: U空为航次空放的燃油成本,美元; F空为船舶空放日耗油量,t/d; D空为船舶空放天,d; S空为船舶空放里程,n mile; v空为船舶空放航速,kn; P为燃油价格,美元/t。
2.2 结果分析
在实践中,摆位货载的卸货港往往并不是下一航次的装货港,大多数航次结束港与下一航次装货港仍然有一段航行里程。方案B选择的摆位货载航次完成港为镇江港,衔接的下一航次装货港为秦皇岛港。该类型摆位航次依然使得船位发生有效位移,有利于下一航次货载的安排(镇江港距秦皇岛港更近)。此类航次租金水平RB重1进行闭环调整后的租金水平为RB1,将式(4)进行延伸,即首先分别计算出船舶执行航次开始船位和结束船位与下一航次装货港的航距差,将船舶空载航行该段航距差时所消耗的燃油成本补贴到该航次效益中,同时在该航次时间中扣除航距差所消耗的时间。该类航次的闭环计算式为
式中:CB重1为航次重载部分的贡献毛益,美元;DB重1为航次重载部分的总营运天,d。
在船舶沿海运输的实际经营过程中,尤其是在执行北上铁矿石货载航次任务时,可以根据已知的船舶规范(航速、日耗油)及港口间里程,测算出其执行航次的闭环期租水平,并与该船舶选择其他经营方式如执行北方港口装煤空放循环航线的期租水平进行比较,从而选择更优方案,进而有效提升经营水平和经营效益。
实践证明,该方法对于多数情况下的摆位航次的闭环调整是可行的。但是,由于该方法对航次营运天进行了调整,在航次总营运天不长而空放时间较长的情况下,容易使闭环后租金水平升高,进而影响经营决策。
2.3 船位价值理论方法
船位价值理论方法是在闭环调整方法的基础上进行部分优化,将摆位航次产生的船舶位移的船位价值加到航次效益中,并不对航次营运天进行调整。基于船位价值理论对航次期租水平进行效益调整,对比摆位航次调整后的租金水平与船舶空放或者选择其他航线的效益水平,得出更优方案。
方案B是典型的摆位航次,即通过该航次的执行,使船舶的位置从广州港摆位至镇江港,从而为下一航次创造了船位价值,因此在对航次期租水平RB重2调整中,将广州港至镇江港航程的船位价值补贴至该航次效益中,调整后期租水平为RB2。该类航次租金水平调整的计算式为
式中: M空为空放期间船期成本,美元; DB为方案B航次开始船位与航次结束船位的航行天,d; RTL为航次期间平均市场期租水平,美元/d。
如果下一航次装货港确定,那么可以将式(7)进一步加以完善,即将船舶执行航次开始船位和结束船位分别与下一航次装货港航距差时所消耗的燃油成本和船期成本价值补贴到该航次效益中。该类航次租金水平调整的计算式为
由以上分析可以看出,船位价值理论方法与闭环调整方法在期租水平调整的理论方面本质上是相同的,不同之处在于是否对营运天进行调整。闭环调整方法数据结果相对更加客观,船位价值理论方法则考虑了市场水平因素,其调整结果因市场水平变化而变动。
3 实例分析
某船从事我国沿海运输业务。该船第m航次于广州港空出后,经海南八所港装运铁矿石至北方黄骅港卸货,航次营运天15.5 d,贡献毛益为美元,期租水平为美元/d。
因第m航次完成港黄骅港恰为北方煤炭装运港,其衔接的第n航次执行经黄骅港装运煤炭至海南洋浦港卸货,该航次营运天为12.9 d,贡献毛益为美元,期租水平为美元/d。
该船为大灵便型船,载质量 t,经济航速如下:空载航速为11.3 kn,耗油19.5 t/d;满载航速为12 kn,耗油20.5 t/d。
广州港至黄骅港航距为 ,黄骅港至洋浦港航距为 ;航次燃油价格为550美元/t;航次期间平均市场期租水平为美元/d。
案例分析如下:
(1)传统分析方法:即将第m航次和第n航次期租水平进行加权平均,得出两航次平均期租水平。应用式(2),计算结果为
(2)闭环调整方法:分别计算第m航次和第n航次闭环后期租水平,计算结果为
(3)船位价值理论方法:分别计算第m航次和第n航次闭环后期租水平,计算结果为
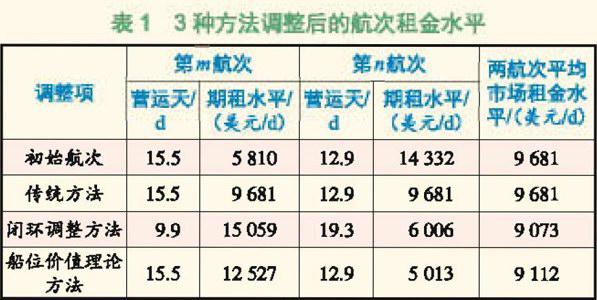
将以上3种方法结果汇总,结果见表1。
以上3种方法均对第m航次和第n航次进行单航次效益调整。由表1可以看出:传统方法计算出两航次平均市场租金水平为美元/d;闭环调整方法和船位价值理论方法对第m航次的闭环调整后的期租水平均大于市场租金水平美元/d,即通过第m航次的摆位效果取得的间接航次效益优于市场船舶空放经营;闭环调整方法和船位价值理论方法对第n航次闭环调整后的期租水平均小于市场租金水平美元/d,表明该航次的经营并未充分利用上一航次的船位价值,其实际取得的航次效益低于市场租金水平。
4 结 语
(1)传统方法计算出两航次实际平均租金水平,需在全部航次实际结束后再进行计算。计算的平均租金水平相对准确,有利于航次后评价,但该方法存在时效性方面的局限,不适合即时性的经营决策。
(2)闭环调整方法是对单航次效益的有效调整方法。该方法对非闭环航线航次尤其是沿海摆位航次进行有效的效益调整,可为船舶经营者在航次计划制订时提供决策支持。同时,该方法对提供摆位货载、执行摆位航线的部分客户评价具有明显的效用,但对航次时间较短或航程较短的航次闭环调整时,调整航次营运天会导致计算结果上下浮动较大。
(3)船位价值理论办法与闭环调整办法理论上相通,但该方法不对营运天进行调整,而是考虑航次船位位移的时间成本。该方法的适用范围更为广泛,但需要经营者对市场波动趋势进行预判,航次执行期间不同的市场租金水平会导致调整结果的不同,同时也需要决策者对摆位航次后的下一航次安排及航次衔接进行提前谋划,因此船位价值理论方法受经营者主观因素影响较大。
本文旨在提供沿海摆位航次效益测算的方法,为船舶经营者即时决策提供决策理论支持。闭环调整方法和船位价值理论方法已经越来越多地应用到经营实践中,船舶经营者可以根据需要,选用其中一种或者将两种方法相结合来测算摆位航次效益以支持决策。
