静中求变，变中寻静

范庆花

【摘要】 每一节课教育者都无法离开教材和教学活动这两个基本要素，如果教材是静态的教学工具，教学活动就是动态的教学形式，而如何在“静”与“变”的平衡之中找到数学知识的切入点，让中学生在复习课中获得知识与能力的 提升.本文以“全等三角形”一课为例，对此进行了全面探析.

【关键词】 数学课堂;教材;教学活动;动静结合

教育就是让每名学生的天性以及他们自身本来就具有的能力得到释放并健康发展，而不是单纯地将外来的知識，灌输进一个“容器”.学生是一个发展中的个体，他们不像已经长大的成人，在某些方面已成定式，他们有着自身的内在价值，而教育者就是充分挖掘这种价值，甚至引导他们创造更大的价值.在数学学习领域，复习课一直都很重要，它不仅是对知识的回忆、回顾，而是对知识体系进一步更全面和更系统的梳理，在数学复习课上，教育者无法脱离的两大要素——教材与教学活动的组织与设计，对复习效果起着直接的关键作用，同时这一“动”一“静”的两大要素，也为学生实现个人能力冲破提供了良好契机.如何引导学生静中求变，变中寻静，在动与静的完美结合中，让学生在能力、价值上实现提升，本文以“全等三角形”一课为例，对此展开了详细阐述.

一、创建主题，动静结合

师：请大家评价一下今天老师的穿着……

生：西装领结很漂亮！

师：如果我换套休闲装，那大家是不是就不认识我了？

生：怎么会，你的衣服虽然换了，但脸没有变，我们当然认识了.

师：没错，同样的道理在数学原理中也适用，只要能够将不变的一个特征抓住，一些问题就会很轻松解决，那么我们就一起看看今天这个主题“变化图形中不变的‘全等”.（课题展示）

师：先看如图1所示，沿对角线AC将矩形ABCD剪开后会得到两个新的三角形.如果将△A′C′D′顶点A′和点A重合，并以点A为中心按逆时针方向旋转该三角形，使B、A（A′）和D三点如图2中所示，在同一直线上，那么哪条线段和BC相等？

∠CAC′等于多少？假设图2中的CA与A′C′不相等，垂直条件仍然有效，那么同学们又会有怎样的结论得出？

学生们很快通过观察和推断，得出了“△ABC与△C′DA′相似”的结论.

师：不错，图2就好像刚才我所提到的老师的脸，只要大家记住了它的特征，即“包含了三个垂直”，那么无论接下来无论老师穿了什么样的外衣在它“身上”，你们都能够认得出来.不信试试看.（通过多媒体将不同形态的包含三垂直的图片展示出来）你们能认得出它们吗？

【设计意图】从生活化的一个小细节开始，学生们的注意力始终没有离开过本课主题.而换了衣服是不是还可以认出教师的话题，和学生生活经验和认知经验相贴近，很大程度上引起了他们的兴趣，且这个话题与本节课核心内容又密不可分，彰显了动中有静，静中有动的辩证统一关系.而从一个关于矩形剪纸的生动形象问题中，直接进入到主题——三垂直图形.不但是从生活向数学的自然过渡，同样也为接下来自主探究做好铺垫.

二、自主探究，静中求变

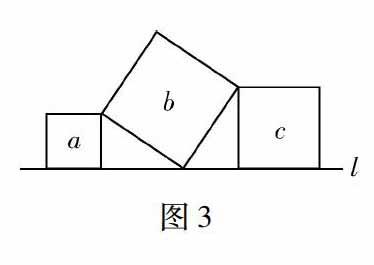
师：大家看一下我接下来要把图2变换一下，就有了图3，观察图3，尝试思考下面的问题：图中有三个正方形在直线l上面，如果正方形a和c面积分别是5与11，那么正方形b面积是多少？将图2与图3进行比较，结合我们刚刚提到关于“变装不变脸”的话题能想到什么？

生：我好像发现了两个三角形应该存在全等关系……

师：需要我帮助标注吗？

学生亲自上前用粉笔标注出来.

师：怎么证明它们全等？

同学们纷纷上前证明……

【设计意图】通过“变式”训练增强问题难度，仿佛在三垂直图形外面就加上了一层新衣，这是从静中求变的一个开始，引导学生开启自主探究模式，对基本图形作用尝试进行自我理解.

师：同学们的证明都很不错，现在我们继续认识新的图形.如图4（1）所示△ABC中，已知∠ABC为直角，AB和BC相等，三角形三个顶点分别与三条直线相平行，并且l1与l2距离是2.l2和l3距离是3，那么AC有多长？大家能不能说一下这个题的思路？

生：从直角中可以想到勾股定理，如果想求AC应该先求AB或者是BC……

师：那AB或者是BC应该如何求？

生：……

师：大家是不是可以看看，图4之中是不是也存在我们之前提到的关于“换装不换脸”的问题？

生：（立刻兴奋状）我知道了，经过A，C做出和l3垂直的垂线，我们就又得到了三垂直图形！问题就解决了！

师：所以说面对类似问题，其关键在哪里？

生：看能不能创造出三垂直图形，获得三角形全等以及相关的信息……

【设计意图】伴随问题难度的不断攀升，学生们获得了更多自主探究、自主发挥以及运用所学经验的机会.将学生独立思考与教师的有效引导结合起来，让学生们拔开若隐若现的华丽外衣，在“不变”之中寻求“变化”，又尝试在“变化”之中找到“不变”.

三、揭示本质，变中寻静

师：我们一下子解决了这么多新问题，看起来好像有点难不住大家了，接下来看看这些问题你们能不能解决？如图5所示的△ABC中，∠ACB是直角，AC和BC相等，直线MN过点C，并且MN分别垂直AD，BE于点D和E，那么能不能证明DE=AD+BE？而如果直线MN绕C点旋转后成为图6，能不能证明DE=AD-BE？同样如果旋转到图7位置，那么AD、DE和BE三者之间又会出现什么样新的等量关系？你们能把等量关系写出并证明吗？

教师可以先引导大家进行独立思考，再建议进行小组讨论.

经过交流讨论之后……

师：能不能说一说这三个问题如果想得到解决，它的关键点在哪里？

生：很明显，应该先找是不是有全等三角形，图5比较明显.

师：不错，那图6呢？

生：也并不太难，可以通过AAS判断△ADC和△CEB全等，然后可以推出它们有相等的对应边，所以AD与CE相等，CD与BE相等.

师：同学们是怎样能快速地就能够判定两个三角形全等的？

生：当直线在图6中位置的时候，AC和BC相等，∠ACB为直角，AD和BE分别垂直直线MN于点D和E，这些条件都没有改变.

师：可是明明图5和图6看上去非常不一样！

生：看上去不一样也只是垂足发生变化了，整个图形并没有实质性改变.

师：那图7……

略做思考之后.

生：可以同样按照上面的思路找到答案.

师：非常棒，那从这三个问题中你们有什么发现？

生：虽然点的顺序与位置都发生了变化，但实质上三垂直图形一直没变.

【设计意图】通过图形的不断“旋转”变化，使问题由静态变动态，是静中求变的深化.接下来在引导学生们深入地去揭示知识本质的过程中，于变中寻静体会到了“万变不离其宗”的思想，无论直线方向，还是垂足位置怎样变化，但始终都能够找到三垂直图形，这是该节内容的本质，同时也是数学知识的本质.

面对当前弊端丛生的教育现状，相信每位教育者都在沉思教育究竟为何？教育究竟应该做些什么？卢梭提出了“教育即生长，生长就是目的，在生长之外别无目的”的论点，一语道破了教育的本质，也为迷茫的教育指明了方向.无论是对教材的精心设计，还是教学活动的科学组织，只要牢牢把握住学生认知规律，不管是静中求变、变中寻静，还是动静结合，都是对新课改“以生为本”的最好诠释.

【参考文献】

[1]王海滨.课堂中的动静结合教学——对数学课堂教学活动的巧妙设计[J].基础教育论坛，2012（1）：30-31.

[2]李青.数学教学中“创新教材，趣味教学”法[J].新课程：小学，2015（5）：130.

[3]左向荣.动静结合，让数学课更高效起来[J].中学生数理化：学研版，2011（11）：67-68.