反例构图丰富多彩，尺规作图蕴含其中

高厚良+陈耀忠

摘要：2017年安徽中考卷第20题难度适中，解法多样，反例构图丰富多彩，动态研究精彩纷呈，试题表述逻辑严密，尺规作图蕴含其中，经典问题，匠心呈现，启示一线教师关注平面几何教学现状，深入思考平面几何教学.

关键词：安徽中考，解法研究，反例构图，教学启示2017年安徽中考卷第20题，取材于教材的反例构造，看似简单，实则内涵丰富，而且解法多样，是一道优秀的平面几何试题，透过试题表象，可以发现中考命题组对当前平面几何教学的深层次思考.本人拟对该题进行赏析，并提出一点自己的思考，请同仁们批评指正.

1试题及解法研究

图1试题（2017年安徽省初中学业水平考试数学卷第20题）如图1，在四边形ABCD中，AD=BC，∠B=∠D，AD不平行于BC，过点C作CE∥AD交△ABC的外接圆O于点E，连接AE.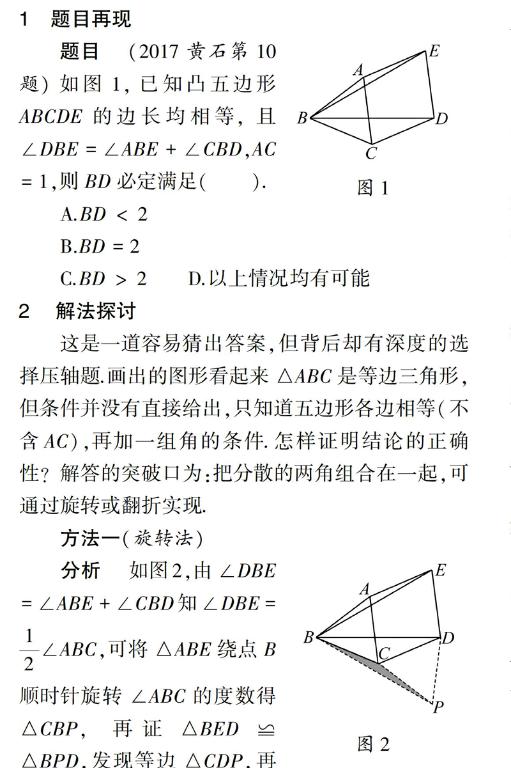

（1）求证：四边形AECD为平行四边形；

（2）连接CO，求证：CO平分∠BCE.

解析对于第（1）问，根据圆周角定理得∠B=∠E，由∠B=∠D，得∠D=∠E.根据平行线的性质与判定可得AE∥DC，故四边形AECD是平行四边形.

说明由于平行四边形的几种判定方法本质上是相通上，故第（1）问还可通过△AEC≌△CDA，借助一组对边平行且相等（或两组对边分别相等或两组对角分别相等）的四边形是平行四边形证明，限于篇幅，此处不再赘述.

（2）对于第（2）问.

图2方法一如图2，过点O作OM⊥EC，ON⊥BC，根据圆中弦与弦心距的关系得OM=ON，进而确定CO平分∠BCE.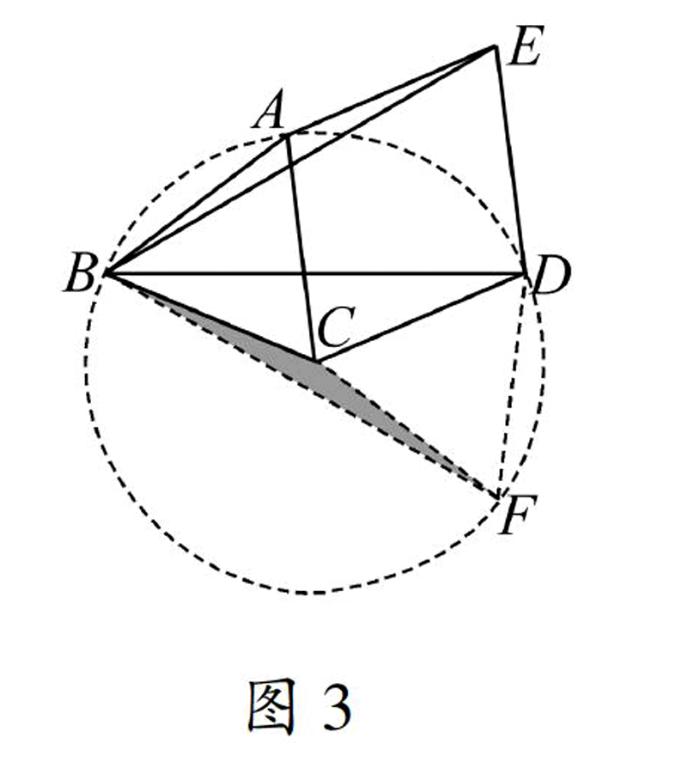

方法二如图3，连接EO，BO，由△CEO≌△CBO（SSS），得∠ECO=∠BCO，即OC平分∠BCE.

方法三如图4，连接EO，BO，BE，由CE=BC，得∠CEB=∠CBE.由OE=OB，得∠OEB=∠OBE，故∠OEC=∠OBC.所以∠OEC=∠OCE=∠OBC=∠OCB.图3图42反例及构图研究

2.1图形简要分析

我们知道“一组对边相等，一组对角相等的四边形是平行四边形”是一个假命题，如何构图说明呢？仔细观察不难发现，本题正好给出一种反例构图的方式：首先画出平行四边形AECD，并作出△AEC的外接圆⊙O，并在⊙O中作EC的等弦BC，四边形ABCD并不是平行四边形.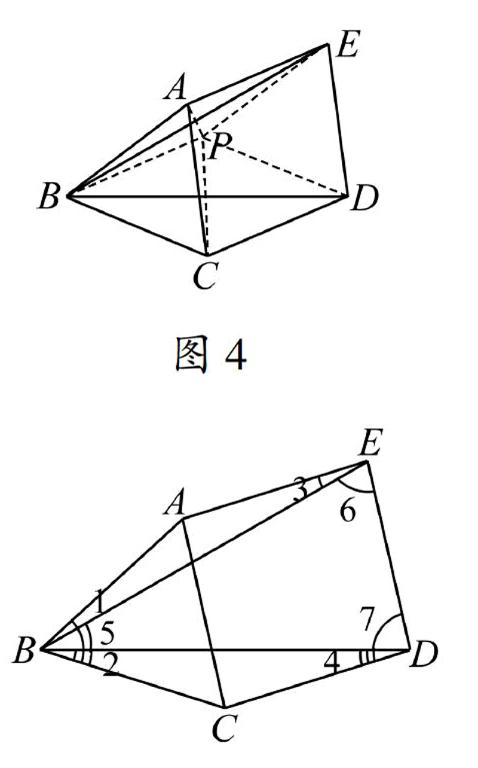

2.2反例其它构图方式

一组对边相等，一组对角相等的四边形不一定是平行四边形作为初中阶段的一个经典问题，其反例构图方式多样，现呈现如下几种：

方法1：如图5，在平行四边形ABCD中，连接BD，把△BCD绕点D旋转得△B′DC′，使点B′落在AB上，则四边形AB′C′D中，∠A=∠C′，AD=B′C′，四边形AB′C′D不是平行四边形.

图5图6方法2：如图6，平行四边形ABCD中，连接BD，以点B为圆心，BD长半径画弧交CD于点D′，把△BCD′绕点B旋转，使BD′与BD重合，得△BC′D，则四边形ABC′D中，AD=BC′，∠A=∠C′，四边形ABC′D不是平行四边形.

方法3：如图7，在△ABC中，AB=AC，在底边BC上取一点D，以点A为圆心，CD长为半径画弧，交△ADC外接圆于点E，连接AE，DE，则在四边形ABDE中，AB=DE，∠B=∠E，四边形ABDE不是平行四边形.

图7图8方法4：如图8，在Rt△ABC中，∠A=30°，∠C=90°，在AC上截取AD=BC，以点D为圆心，AD长为半径画弧，交AB于点E，则四边形BCDE中，DE=BC，∠B=∠CDE，四边形BCDE不是平行四边形.

方法5：如图9，两等圆⊙O1，⊙O2相交于A，C两点，在⊙O1上取一点B，以C点为圆心，AB长为半径画弧，交⊙O2于D，E两点，则四边形ABCD中，AB=CD，∠B=∠D，四边形ABCD不是平行四边形.

图9图102.3对试题中某些条件的思考

2.3.1试题中为什么刻意强调AD不平行于BC

四边形ABCD中，AD与BC有两种位置关系，平行或不平行，此处若不强调AD与BC的位置关系，则需分类讨论，显然难度有所提高，但在问题解决过程中，却有重复之嫌，不能很好地体现出数学的简洁之美.

2.3.2在图1的构图过程中，∠EAC的大小是否有限制

如图10，当∠EAC=90°时，CE是⊙O直径，根据CE=CB可得，CB也为⊙O直径，即CE，CB重合，AD∥BC，与已知矛盾，故∠EAC≠90°.

进一步研究会发现，如图11，当点A为定点，C、E两点在弦AB两侧时，90°<∠EAC<180°，如图12，当点A为定点，C、E两点在弦AB同侧时，0°<∠EAC<90°.

图11图123对教学的启示

3.1坚守《课程标准》底线，注重挖掘教材，从教材中寻找教学素材

《课程标准》對教师的教，学生学的程度、方式等提出了明确的要求，是师生进行教学的最低要求，而教材是实现《课程标准》要求的最重要载体.在教学中，应充分利用教材中的例题、习题、阅读素材等，深入研究，适度改编，根据学生认知规律，教学的需要合理地进行整合，串联，做到源于教材高于教材.本题即取材于课本，同时在教师用书课程资源的教学链接部分也给出了假命题的一个反例构图方式.结合近几年安徽中考卷中的几何题不难发现，不但给教学提供了丰富的素材，也对教师如何跳出题海，立足课本中的基本图形，揭示图形间的内在联系，构造新的问题等提出了要求.

3.2重视基本图形，向经典致敬，注重数学研究的基本方式，基本流程的渗透

试题有背景，题后有“故事”，是安徽中考近几年几何试题设置上的一个显著特点，素材选取向经典致敬.如2016年第22题“阿基米德穷竭法”的再现，第23题“费马点”构图在问题解决中的应用，2017年第10题“将军饮马”对称模型的考查，第20题“反例图”的构造，第23题将“弦图”、“古埃及三角形”、“黄金分割”三位一体地融合等，无不体现这一特点.进一步研究不难发现，第20题还适度展示了数学研究的基本过程：确认数学研究对象——研究对象性质——思考判定方法（往往是性质的逆命题）.本题先给出了一个错误判定方法的反例图，请孩子们完成一个正确判定方法的定理，是教材内容的深入与继续，是从性质走向判定经常研究的话题，也是试题研究经常采用的方式之一.

3.3尊重现实，加强尺规作图，切实提高学生的构图能力

能否借助所学知识，利用尺规作图解决问题是体现学生数学素养高低的重要标准之一.近年来安徽中考虽没有直接考查过尺规作图，但研读2017年安徽中考卷却不难发现，命题组还是适当加强了对尺规作图的考查.第20题各种反例图的构造，就不是轻易可以完成的，同时在题目的呈现上，所有问题极其严格讲究，试题严格按照相关几何元素出现的逻辑顺序给出，按照题目条件就可以做出相应的几何图形，为试题的研究提供了保证.再如第18题，安徽中考的必考项目网格作图也较往年有了一点点的变化，增加了通过构图把两个角的和转化为一个等腰直角三角形一个底角的考查，这些都渗透了命题组对当前几何教学的一些思考：针对当前平面几何教学课时的减少及阅卷中出现的比较严重的逻辑混乱现象，如何在有限的平面几何教学内容及课时中培养学生的构图能力、逻辑推理能力，其考查路径如何选择等.这些试题的轻微变化所传递出的信息值得一线教师认真思考.endprint