中考命题视角下数学思想教学的思考

钟珍玖+朱炎林

思想方法是数学教学中重要内容之一，值得广大数学教学工作者进行深入的研究.笔者经历了2017年无锡市数学中考命题工作，对数学思想方法的教学有了更深刻认识.本文试图结合试题命制谈数学思想方法的教学，请同行斧正.

1关于数学思想方法及其教学的理解

1.1关于数学思想方法

对此，数学家和数学教育家有诸多论述，大多倾向于从“数学思想”和“数学方法”两个角度进行阐述，认为数学思想是对数学对象本质的认知，是从具体的数学概念、命题、方法等的认识过程中概括出来的基本观点和根本方法.数学思想是数学的灵魂，是数学学科区别其它学科的重要标志之一，是内隐的数学知识，对学生的思维的发展起到至关重要的作用.而数学方法是指数学活动中所采用的途径、方式、手段、策略等，是对数学问题所进行的具体的操作.这些都是结合数学的本质特征，基于哲学与方法论的抽象阐述.

1.2关于数学思想方法教学的理解

根据中学生的认知特点，课堂教学中，没有可能也没有必要对思想方法进行理论研究，重要的是引导学生经历问题探究活动过程，掌握数学问题解决策略，感悟数学思想方法，形成必要的数学技能和数学认识策略.初中阶段常见的数学思想：转化和化归思想、数形结合思想、函数与方程思想、建立数学模型思想、统计思想等；常用的数学方法有：消元法、降次法、配方法、待定系数法、公式法、图像法等，只有灵活运用数学思想方法，学生的思维能力和数学学习能力才能得以提高.

2中考命题视角下数学思想方法的教学思考

2.1重视命题对数学思想方法教学的导向作用

中考命题不仅是对学生学业水平的评价，更在于对区域内数学教学的导向作用，引领区域内教师教学的方向，对教师的教和学生的学产生广泛而深远的影响.毋容置疑，对重要思想方法的考查是数学中考试题的重要内容.教学中，教师要注重研究重要而常考的数学思想方法，并在教学中予以高度重视.

案例1（2016年无锡）如图1，已知OABC的顶点A、C分别在直线x=1和x=4上，O是坐标原点，则对角线OB长的最小值为.

图1解连接AC，交OB于点D，因为OABC为平行四边形，所以OD=BD，AD=CD，所以由中点公式可得点D横坐标xD=25，xB=5，（也可由三角形全等或相似求点D、B的横坐标）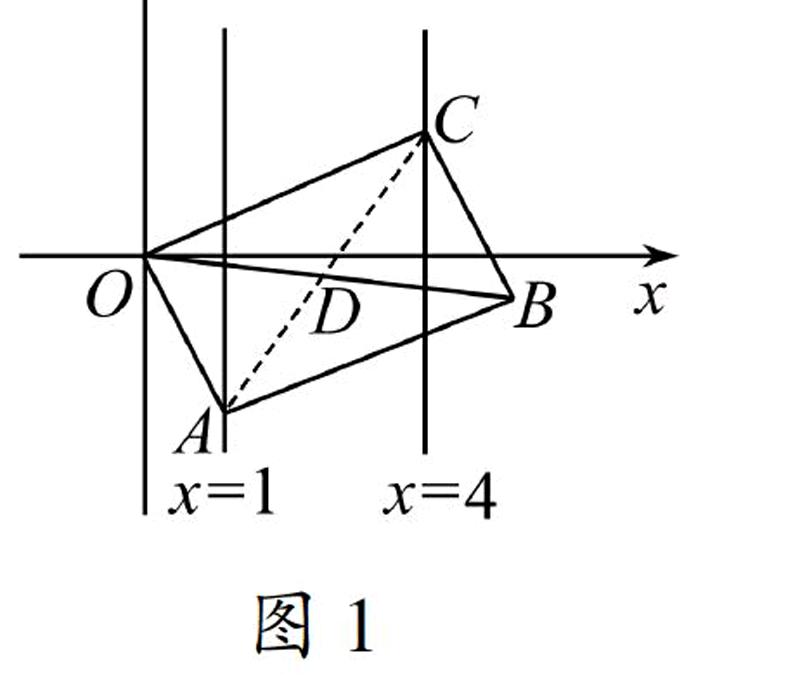

所以点B在x轴上时，OB最小值为5.

教学思考本题难点在于OABC的顶点有三个动点，对求角线OB长的最小值缺乏策略.如果数学思想认识深刻，问题解决比较容易入手.点A、C虽然是动点，但运动的轨迹在直线x=1和x=4上，而四边形OABC的形状是不变的，这样就隐含了两对角线的交点横坐标是25，所以点B的橫坐标是定值5，容易发现点B在x轴上时OB的最小值为5.线段的最值问题是教师教学的重点，学生的练习量比较大，但面对此题还是有很多学生束手无策.命题者会对学生平时的练习题作一些变化和变式，虽然问题呈现的形式变了，但是数学本质没有变，所以教师的教学要以中考的评价为导向，把数学思想方法的教学落实到每节课上，以不变应万变，学生面对中考的能力题才会游刃有余.

2.2重视数学问题对数学思想方法的“外显”作用

数学问题是数学思想方法的载体，所谓的“难题”就表现在含有丰富的数学思想，但是，数学思想方法一般都是内隐的，这就造成学生的思维障碍.所以教学要在问题解决过程中揭示数学思想，让内隐的思想方法外显化，以有利于学生的感悟与内化，达到驾轻就熟的地步.

案例2（2016年无锡）如图2，已知ABCD的三个顶点A（n，0）、B（m，0）、D（0，2n）（m>n>0），作ABCD关于直线AD的对称图形AB1C1D.图2（1）若m=3，试求四边形CC1B1B的面积S的最大值.

（2）若点B1恰好落在y轴上，试求nm的值.

解（1）如图3，BB1交AD于点E，CC1交AD于点F因为AB1∥DC1，AB∥DC，所以∠B1AB=∠B1AE+∠BAE=∠C1DA+∠CDA=∠C1DC，因为AB1=DC1，AB=DC，所以△B1AB≌△C1DC.所以△B1AB的面积S1与△C1DC的面积S2相等.所以S=2S□ABCD=2×（3-n）×2n=-4n2+12n=-4（n-32）2+9.所以当n=32时，S最大值为9.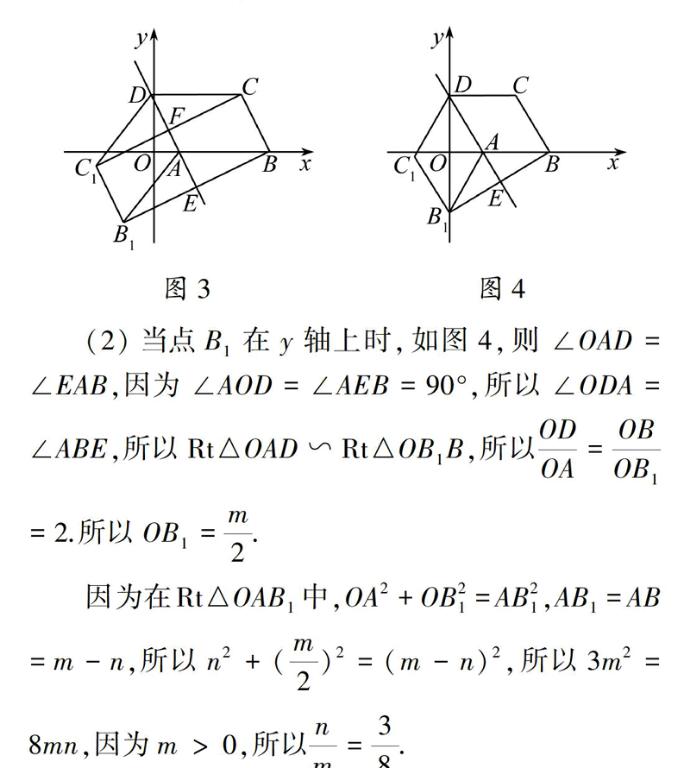

图3图4（2）当点B1在y轴上时，如图4，则∠OAD=∠EAB，因为∠AOD=∠AEB=90°，所以∠ODA=∠ABE，所以Rt△OAD∽Rt△OB1B，所以ODOA=OBOB1=2.所以OB1=m2.

因为在Rt△OAB1中，OA2+OB21=AB21，AB1=AB=m-n，所以n2+（m2）2=（m-n）2，所以3m2=8mn，因为m>0，所以nm=38.

教学思考首先，题目中含有两个参数m、n，其共同决定了ABCD的形状、大小和位置，第（1）题中m=3，四边形CC1B1B的面积就可以用n表示，即用字母表示图形面积的变化.第（2）问确定点B1的位置，即通过图形的特殊位置来确定m、n之间蕴含的关系，从确定图形位置中发现包含的数量关系，通过相似和勾股定理构造方程解决问题，将几何问题代数化，体现了数与形的紧密联系.其次，问题中蕴含的“动”、“静”关系也非常深刻，纵观这道中考试题表面看来是静止的，实际上A、D、B的坐标都是用字母表示的，由于字母表示数的一般性，就蕴含了动态的思想，△CDC1、△BAB1可以看作平移，这些也是“动”的，题目中给出了“ABCD沿直线AD翻折变化”是动态的过程.但D（0，2n），A（n，0）中隐含着OA︰OD=1︰2告诉我们∠ODA的度数不变，除此之外，AD垂直平分BB1，△ODA、△EBA、△OBB1、△EDB1（图4中）是相似的直角三角形，△B1AB与△C1DC是全等的三角形，四边形CC1B1B是矩形……这些都是不变的，发现“动”与“静”的过程，是思维不断走向深入的过程，也就可以找到解决问题的方法和途径.发现四边形CC1B1B是矩形可以直接求矩形CC1B1B的面积，发现△B1AB全等于△C1DC，可以用割补法求四边形CC1B1B的面积.第（2）小问则化“动”为“静”，找到运动的特殊位置B1在y轴上，仍然是利用不变的关系，Rt△OAD与Rt△OB1B相似不变性来解决问题.在运动中发现不变量是解决问题的关键，也是问题的本质所在.这些隐含在问题中的思想需要教师在教学中不断挖掘，给学生以示范，以期学生对数学本质有更深刻的认识.endprint

2.3重视数学思想方法在解题策略形成中的指向作用

笔者认为，数学解题的关键在于策略的选择.影响解题策略形成的因素很多，但对于数学思想方法的领悟是策略形成的“风向标”，也是解决数学问题的利器.

案例3（2017年无锡）在如图5的正方形方格纸中，每个小的四边形都是相同的正方形，A、B、C、D都在格点处，AB与CD相交于O，则tan∠BOD的值等于.

图5解连接EF、AE，则EF∥CD，所以∠BOD=∠AFE，因为EF=2，AE=32，AF=25，所以EF2+AE2=AF2，所以∠AEF=90°，所以tan∠BOD=tan∠AFE=AEEF=3.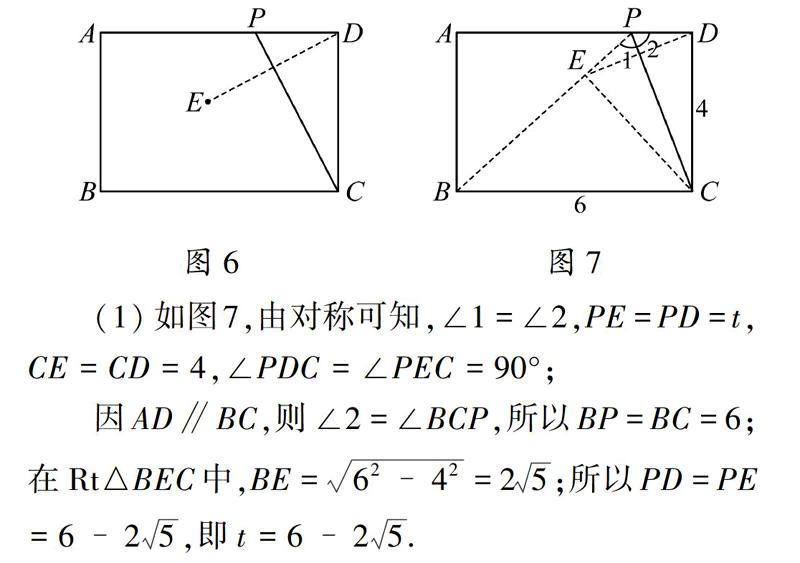

本题还可以通过平移线段AB构造直角三角形，或者同时平移AB、CD构造等腰三角形来解决问题，读者可以自行尝试.

教学思考求∠BOD的三角函数值的关键是构造直角三角形，比如：从A、B、C、D四点作直线AB或CD的垂线，但由于垂足不在格点上，问题难以解决.故要另辟蹊径，运用“转化”思想，将∠BOD用其他的角代替，这个角又恰好在某一个直角三角形中.考虑画CD的平行线EF（如图5），连接AE，这样就构造了直角△AEF进而求出∠AFE的正切，从而求出tan∠BOD的值.这里抓住了等角转换，问题在方向上就正确了，显然“转化”思想是形成解题策略的关键.另外，CD是5×5的网格图正方形对角线，EF是1×1的网格图正方形对角线，发现CD平行EF，构造Rt△AEF也体现了数形结合的思想.这个过程不仅是数学思想的妙用，更体现了思维创新.

2.4重视数学思想方法对思维品质形成的促进作用

数学教育的一个重要目标就是培养学生良好的思维品质，数学学科对于培养学生思维敏捷性、严密性、深刻性有着其他学科无与伦比的优势.中考承担了毕业和升学的双重功能，对于学生的思维能力的考查自然是考试的重点之一，所以教师的教育要把培养学生思维能力和思维品质放在突出重要的位置，數学思想方法的教学促进学生思维品质形成的必然选择.由于数学知识的本质由数学概念原理和解决问题所反映的思想方法来体现，因此使学生掌握了数学思想方法就是使思维品质的形成落到实处.

案例4（2017年无锡）如图6，已知矩形ABCD中，AB=4，AD=m.动点P从点D出发，在边DA上以每秒1个单位的速度向点A运动，连接CP，作点D关于直线PC的对称点E.设点P的运动时间为t（s）.

（1）若m=6，求当P、E、B三点在同一直线上时对应t的值.

（2）已知m满足：在动点P从点D到A点的整个运动过程中，有且只有一个时刻，使点E到直线BC的距离等于3，求所有这样的m的取值范围.

图6图7（1）如图7，由对称可知，∠1=∠2，PE=PD=t，CE=CD=4，∠PDC=∠PEC=90°；

因AD∥BC，则∠2=∠BCP，所以BP=BC=6；在Rt△BEC中，BE=62–42=25；所以PD=PE=6–25，即t=6–25.

（2）①如图8，当P点运动到A，且E点落在到BC边上方且到BC的距离等于3时，作EF⊥CB交CB的延长线于F，延长FE交DA的延长线于H.

在Rt△HEP中，由勾股定理可得：1+（7–t）2=t2，解方程得：t=477，即m=477.

②如图9，当P点运动到A，且E点落在BC边下方且到BC的距离等于3时，作EF⊥DC交DC的延长线于F，延长FE交AB的延长线于M.

在Rt△PEM中有：（m–7）2+72=m2，解得m=47.当0

图8图9教学思考本题的背景是矩形，一边用参数来表示，其形状是可以变化的.第（2）问需要一定的空间想象能力和较强的理解能力，特别是使点E到直线BC的距离等于3，这样的点在“平行于BC且距离等于3的两条直线上”，进而用分类讨论的方法求出t的范围，用动态的观点找出有且只有一个时刻，使点E到直线BC的距离等于3.很多考生反映不能理解题目的意思，造成漏解和误解.问题的表述简洁，但却蕴含着很多数学思想，问题的解决需要考生具有缜密的思维能力，对数学问题有深刻的理解和对数学思想方法的领悟.

重要数学思想方法重点考查，以考查学生挖掘和应用数学思想方法的能力，这是命题者的追求.在教学中，只有不断渗透数学思想方法，加深学生对数学思想方法的领悟、运用和内化，学生的数学素养才能得到真正的提升.

作者简介钟珍玖（1971—），男，教育硕士，中学数学高级教师，无锡市数学学科带头人.曾获无锡市优秀班主任、市优秀教育工作者等荣誉称号.发表论文30多篇，其中有3篇被人大资料复印中心全文转载，参编《初中数学有效教学》、《初中数学有效学习评价》等专著.