漫谈思维定势的“立”与“破”

1缘起——师生解法对决

在进行初三期中复习时，碰到如下问题：

题目（2012年深圳）如图1，在平面直角坐标系中，直线l：y=-2x+b（b≥0）的位置随b的不同取值而变化.已知⊙M的圆心坐标为（4，2），半径为2.

（1）当b=时，直线l：y=-2x+b（b≥0）经过圆心M；

（2）当b=时，直线l：y=-2x+b（b≥0）与⊙M相切；

（3）略.

对于第（1）题，直接代入圆心坐标即可，b=10；对于第（2），教师和学生的思路如下.

①当直线l与⊙M相切，设切点为C，连接MC，作ME⊥OX，则ME=2=r，E为切点，作CG⊥ME，CH⊥OX.

②由△CGM∽△AOD，MGCG=ODOA=12，且MC=2，求出MG=255，CG=455.

③故OH=4-455，CH=2-255，即求出C点坐标为（4-455，2-255）.

④最后代入直线y=-2x+b，从而b=10-25.

同理求出另一条切点C′（4+455，2+255），从而求出b=10+25（见图3）.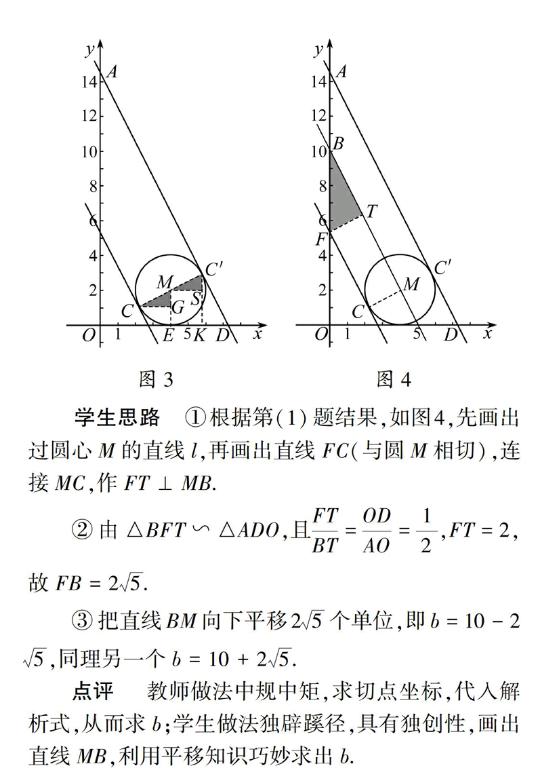

点评教师先求出点C坐标是关键，用点坐标代入直线解析式求出b是常规手段！图3图4学生思路①根据第（1）题结果，如图4，先画出过圆心M的直线l，再画出直线FC（与圆M相切），连接MC，作FT⊥MB.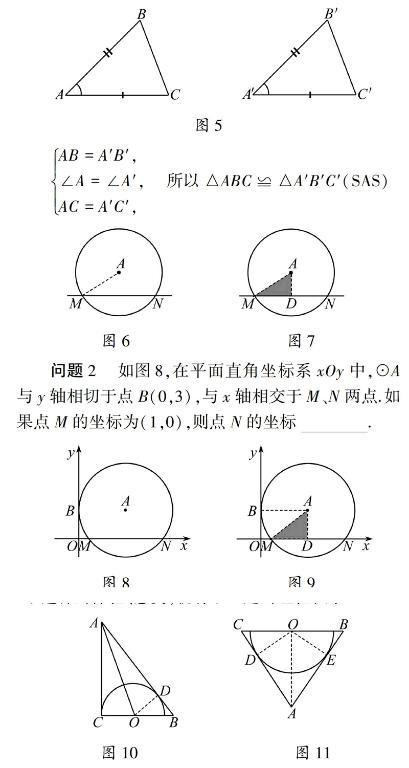

②由△BFT∽△ADO，且FTBT=ODAO=12，FT=2，故FB=25.

③把直线BM向下平移25个单位，即b=10-25，同理另一个b=10+25.

点评教师做法中规中矩，求切点坐标，代入解析式，从而求b；学生做法独辟蹊径，具有独创性，画出直线MB，利用平移知识巧妙求出b.

反思求b，为什么一定要先求出C点坐标呢？学生为何能画出这样漂亮的直线MB呢？学生怎么想到平移已知直线MB来求解而教师却不能？

2厘清概念——“思维定势”解析

思维定势是心理学定势理论术语.定势是一定的心理活动所形成的一种预先的心里准备状态，它使人们以比较固定的方式进行认知或作出反应，并影响问题解决时的趋向性.这种趋向性有时有利于问题的解决，起到积极的正效应；有时却妨碍问题的解决，起到消极的负效应.鉴于思维定势具有双重性，应培养学生有利于正效应的思维定势，防止和克服产生负效应的思维定势.

3思维定势的“建立”——解题有法

学生解题过程，就是思维定势的建立过程.所谓熟能生“巧”，就是人们大脑皮层中形成的某种固定联系，是自然而然的想法.

3.1通过观察，学会模仿是建立思维定势的有效手段

案例1学习全等三角形判定方法，为什么教材都给出这样的格式？

图5AB=A′B′，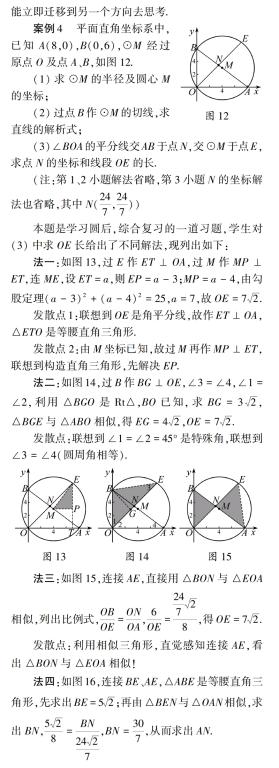

∠A=∠A′，

AC=A′C′，所以△ABC≌△A′B′C′（SAS）

對于初学者，强调这样的书写格式，就是让学生模仿，创造源于模仿，学生多次训练后，就形成正向、强烈的思维定势，为平面几何学习夯实了基础.

案例2例如在圆中已知弦长，求半径，一般做法是构造含弦、半径、弦心距的直角三角形.

问题1如图6，在⊙A中，半径为5，弦长MN=8，则A到MN的距离=.

思路解析上述问题，教师引导学生构造Rt△，如图7，过A作AD⊥MN，求得AD=3；归纳，在圆中经常要构造含弦、半径、弦心距的直角三角形，学生通过观察，也接受了这一结论.

图6图7问题2如图8，在平面直角坐标系xOy中，⊙A与y轴相切于点B（0，3），与x轴相交于M、N两点.如果点M的坐标为（1，0），则点N的坐标.

图8图9思路解析受上述问题1暗示和影响，先连接AB，仿照上述做法，如图9，作AD⊥MN，连接AM，产生Rt△，AD=3，OM=1，设半径为r，则（r-1）2+9=r2，r=5.

反思问题2很快解决，学生已经积累了基本经验，显然这一做法是思维定势的积极作用.这种正向思维定势，提高了学生解题能力.由此可知，在学习新知识初期，要引导学生建立某种思维定势，使学生解题有一般思路，做到有章可循，有法（法则、定理）可依.只有建立了相应的思维定势，才能说学生已经掌握某种知识和方法.

3.2熟练掌握概念、定理、公式、法则等并能正确应用是建立思维定势的基础

如证直线与圆相切，一般做法是充分利用“d=r”这一性质.（d为圆心到直线的距离，r为圆半径）

案例3

问题1如图10，在Rt△ABC中，∠ACB=90°，∠BAC的平分线交BC于点O，以点O为圆心OC为半径作半圆，求证：AB为⊙O的切线.

思路解析教师引导学生先判定直线AB与⊙O交点情况，再作垂线OD（OD⊥AB），下证OD=r，利用角平分线性质即可.教师强调证切线即证“d=r”，并总结直线与圆交点未明确时，可作垂直，证半径.学生有了这样的体验、感受，就有了一定的经验积累.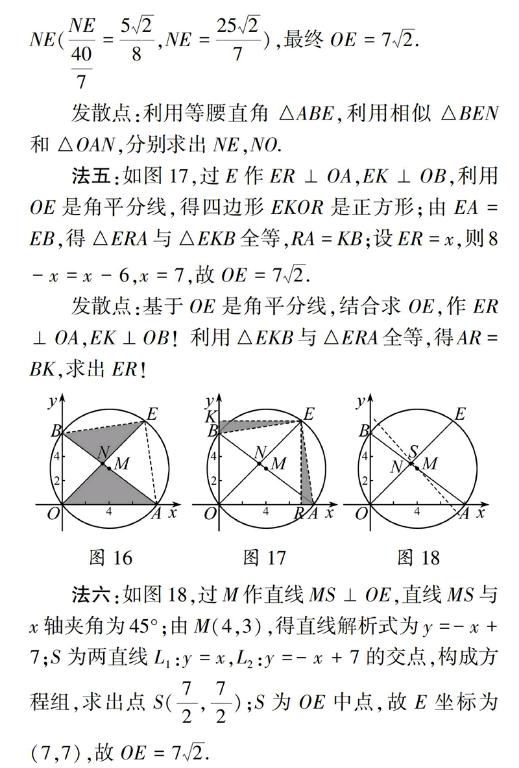endprint

思路解析受到上述案例的思维定势，证明AB与⊙O相切，先连接OD，OA，再作垂直（OE⊥AB），下证OE=r，一次成功.显然，学生在切线证明问题上已经有一定的思维定势，且这种定势是正向的，从而提高了解题能力.只要新旧问题的实质类似，思维定势就起到正效应.

4思维定势的“突破”——解无定法

思维定势具有正效应，对于解决问题很重要，我们常说教师的解题“经验”丰富，就是说的思维定势的积极一面.但思维定势使解题者的思路总是沿着固定的轨道进行，从而限制了创造性的发挥，难以产生新的思路，新的想法.当问题条件发生质的变化，思维定势会使解题者墨守成规，造成知识和经验的负迁移，使解题陷入困境.如何突破思维定势？

4.1一题多解培养发散思维——“突破”思维定势

发散思维就是从某一点出发，不依常规，寻求变异，进行放射性联想，得出多种想法、解法.它往往从不同的角度考虑思维对象，扩大思维的联想度，完成“虚”和“实”的转化，从而在思维的某个方向受阻时，能立即迁移到另一个方向去思考.

图12案例4平面直角坐标系中，已知A（8，0），B（0，6），⊙M经过原点O及点A、B，如图12.

（1）求⊙M的半径及圆心M的坐标；

（2）过点B作⊙M的切线，求直线的解析式；

（3）∠BOA的平分线交AB于点N，交⊙M于点E，求点N的坐标和线段OE的长.

（注：第1、2小题解法省略，第3小题N的坐标解法也省略，其中N（247，247））

本题是学习圆后，综合复习的一道习题，学生对（3）中求OE长给出了不同解法，现列出如下：

法一：如图13，过E作ET⊥OA，过M作MP⊥ET，连ME，设ET=a，则EP=a-3；MP=a-4，由勾股定理（a-3）2+（a-4）2=25，a=7，故OE=72.

发散点1：联想到OE是角平分线，故作ET⊥OA，△ETO是等腰直角三角形.

发散点2：由M坐标已知，故过M再作MP⊥ET，联想到构造直角三角形，先解决EP.

法二：如图14，过B作BG⊥OE，∠3=∠4，∠1=∠2，利用△BGO是Rt△，BO已知，求BG=32，△BGE与△ABO相似，得EG=42，OE=72.

发散点：联想到∠1=∠2=45°是特殊角，联想到∠3=∠4（圆周角相等）.

图13图14图15法三：如图15，连接AE，直接用△BON与△EOA相似，列出比例式，OBOE=ONOA，6OE=24728，得OE=72.

发散点：利用相似三角形，直觉感知连接AE，看出△BON与△EOA相似！

法四：如图16，连接BE、AE，△ABE是等腰直角三角形，先求出BE=52；再由△BEN与△OAN相似，求出BN，528=BN2427，BN=307，从而求出AN.

最后再由该对相似三角形，利用比例线段，求出NE（NE407=528，NE=2527），最终OE=72.

发散点：利用等腰直角△ABE，利用相似△BEN和△OAN，分别求出NE，NO.

法五：如图17，过E作ER⊥OA，EK⊥OB，利用OE是角平分线，得四边形EKOR是正方形；由EA=EB，得△ERA与△EKB全等，RA=KB；设ER=x，则8-x=x-6，x=7，故OE=72.

发散点：基于OE是角平分线，结合求OE，作ER⊥OA，EK⊥OB！利用△EKB与△ERA全等，得AR=BK，求出ER！

圖16图17图18法六：如图18，过M作直线MS⊥OE，直线MS与x轴夹角为45°；由M（4，3），得直线解析式为y=-x+7；S为两直线L1：y=x，L2：y=-x+7的交点，构成方程组，求出点S（72，72）；S为OE中点，故E坐标为（7，7），故OE=72.

发散点1：OE为圆中弦长，作直线MS⊥OE，求出S点坐标，即可解决问题.

发散点2：由角平分线OE，且MS⊥OE，S看成直线y=-x+7和直线y=x的交点，求出S点，最终求出OE长.

4.2解后反思培养收敛思维——“突破”思维定势

收敛实质是一种概括，它要求根据对事物已有经验，找出知识、技能、或解决问题的关键点.换句话说，就是回答了为什么这样做和如何做的问题.在上述学生解法中，组织学生进行解后反思，为何这么做？如何做？

案例4中求线段长度的方法有：

（1）构造Rt△ETO、Rt△EMP，运用勾股定理解决问题；（法一）

（2）构造等腰Rt△BOG，Rt△BEG（与Rt△ABO相似），运用等腰直角三角形和相似知识解决问题，分段求出OG，EG；（法二）

（3）在圆背景下，求线段长一般可以考虑通过相似解决；（法三）

（4）利用相似三角形，分段求出NE，NO，最终求出OE（OE=NE+NO）；（法四）

（5）利用全等三角形知识巧解求AR，最终求出OE；（法五）

（6）在圆背景下，求弦长，作垂线，构造Rt△，巧妙利用交点S，S为OE中点.（法六）

通过师生共同归纳总结，得出初中阶段求线段长的基本方法：即构造直角三角形和利用相似三角形；可以整段求，也可以分段求.有一般方法，但也不拘泥于一般方法，关键在于你思考的角度.法五和法六具有创造性，突破常规想法，值得点赞！

4.3正难则反培养逆向思维——“突破”思维定势

教师和学生在思考问题时，都习惯于正向思考，但有些数学问题，从正面解决不易上手或较繁琐，这是若从反面思考，往往有奇效！

案例5若将抛物线y=ax2+bx+c向右平移2个单位，再向上平移1个单位，两次变换后的抛物线解析式是y=x2+1，则原抛物线的解析式是.endprint

思路解析若从正面y=ax2+bx+c出发思考，就比较繁琐.但逆向思考，从y=x2+1开始倒推，解法简捷，一步到位.y=x2+1先向左平移2个单位，得y=（x+2）2+1，再向下平移1个单位，得y=（x+2）2.

5关于思维定势的思考

本文一开始涉及到的问题，就是教师思维定势负效应的体现.思维定势是一把双刃剑.它为我们解决问题提供了思路和方法，而且是学生获取知识，提高解题能力的重要手段.但有时对思维的创造性和发散性产生限制.

数学教学的目的就在于建立符合数学思维要求的，具有哲学方法论、数学方法论意义上的思维定势.这种心理定势不仅是数学观点系统的重要组成部分，而且是数学思维能力的具体表现，成为数学核心素养的重要标志.在日常数学教学中，通过建立、发展、突破、再建立、再發展、再突破来强化上述定势以达成新心理特征，从而最终发展学生的数学思维能力.

作者简介程军（1971—），男，江苏无锡人，中学数学高级教师，无锡市中学数学教学能手.有20多篇文章在省级杂志上发表或获奖，多篇文章在区级、市级杂志上发表或获奖.其中有3篇数学文章被人大资料报刊复印中心转载.

《数学教育学报》

《数学教育学报》是中国联合国教科文组织指导刊物，王梓坤院士任编委会主任，天津师范大学王光明教授任主编，全国90多家理事单位集资办刊，天津师范大学为主办单位，北京师大、华东师大、东北师大、南京师大、贵州师大、西南大学、扬州大学、浙江师大、首都师大、湖南师大、华南师大、广州大学、江苏师大、华中师大、陕西师大、云南师大、西北师大、佛山科学技术学院等18所高校为协办单位，是目前国内数学教育领域最高层次的学术性刊物.《学报》现为“全国中文核心期刊”、“中国科技核心期刊”、“CSSCI来源期刊”和“RCCSE中国核心学术期刊（A）”.被中国科技论文统计源期刊、中国学术期刊综合评价数据库、中国学术期刊（光盘版）、中国期刊网、中国数学文摘、中国数学文献数据库、美国《数学评论》（MR）、德国《数学文摘》（ZBI）、中国人民大学报刊复印资料等收录.

《学报》宗旨：服务于中小学数学教育改革及高等数学课程改革，倡导数学教育科学学术争鸣与评论，推动国内外数学教育学术交流，建构中国数学教育理论，反映国内外数学教育实践与改革的新成果，发挥对我国数学教育研究与实践的指导作用.

《学报》倾力将用得上的先进理论，可借鉴的国内外数学教育改革经验，带有启迪性的学术争鸣，中小学数学教改的丰硕成果，前瞻性的中小学及高等数学教育改革理念与实证性研究结论奉献给有志于数学教育事业的广大中小学、大学数学教师数学教育科研工作者.

《数学教育学报》为双月刊，104页，大16开，2018年全年订价60元.

欢迎有志于数学教育科研及数学教改的广大中小学数学教师、高等院校从事数学教育教学、科研及理论工作者到当地邮局订阅.欢迎新老读者踊跃投稿.

邮局邮发代号：6—132

编辑部地址：天津市西青区宾水西道延长线393号天津师范大学129信箱《数学教育学报》编辑部

邮政编码：300387电话：022-23766679

E-mail∶sxjyxbbjb@vip.163.com网址：http：//www.sxjyxb.comendprint