波形钢腹板对多跨桥梁刚度贡献率的定量分析

陈 钒， 黄国华， 刘怡辉

(1.中电建路桥集团有限公司, 北京 100000； 2.中电建路桥集团有限公司华中分公司, 河南郑州 450000)

波形钢腹板对多跨桥梁刚度贡献率的定量分析

陈 钒1， 黄国华1， 刘怡辉2

(1.中电建路桥集团有限公司, 北京 100000； 2.中电建路桥集团有限公司华中分公司, 河南郑州 450000)

文章以国内第一座采用整体式顶推施工的大跨度波形钢腹板PC组合梁桥为例，依据材料力学理论，利用等效刚度法推导波形钢腹板刚度贡献公式，并采用解析计算和数值模拟计算导梁挠度，与多跨波形钢腹板箱梁桥顶推现场实测值进行对比，定量验证波形钢腹板刚度对箱梁桥抗弯刚度的贡献，同时证实了考虑波形钢腹板刚度贡献的解析计算更接近实测值。

波形钢腹板； 等效刚度； 抗弯刚度； 挠度

近年，由于波形钢腹板预应力混凝土组合箱梁桥稳定性好、强度高、结构外形美观、抗震性能好、工期短、成本低等多项优点，其受力特性研究已引起国内外学者的广泛兴趣。在国外，已取得较多的研究成果，如1993年Elgaaly和Hajnilton[1]等对其进行了试验研究并通过有限元分析验证了：波形钢腹板梁抗弯能力由翼缘决定，腹板对抗弯的贡献可以忽略。腹板几乎承担了全部的剪力；结构破坏比较突然，首先是受压翼缘屈服，随后腹板屈曲。日本学者Machidamrong[2]等应用变分原理提出了相似于经典Timoshenko梁理论的扩展梁理论，并通过试验研究和有限元分析验证了这一理论的可行性。在国内，学者们对于波形钢腹板组合箱梁桥的挠度计算方法和抗弯性能也进行了广泛研究。如李宏江等[3]通过模型试验和有限元验证剪切变形对波形钢腹板简支箱梁的挠度影响；苏俭等[4]和刘保东等[5]分别从能量变分法和有限元分析方法研究了波形钢腹板挠度计算方法并进行了验证；聂建国等[6-7]将波形钢腹板组合箱梁的横向受力行为分解为桁架作用和弯曲作用，建立了一个能够考虑波形钢腹板剪切变形的梁理论模型，并给出了特定条件下的解，同时也通过有效刚度法推导了在正常使用极限状态下的挠度计算公式，提供了一种准确性较高的简化计算方法。但上述研究大多基于理论计算、数值模拟和模型试验，缺乏现场实证研究。此处在解析计算和数值模拟的基础上，结合郑州陇海路常庄干渠波形钢腹板箱梁桥顶推施工监测数据，分析验证考虑波形钢腹板刚度对桥梁整体抗弯刚度的贡献。

1 波形钢腹板等效刚度计算

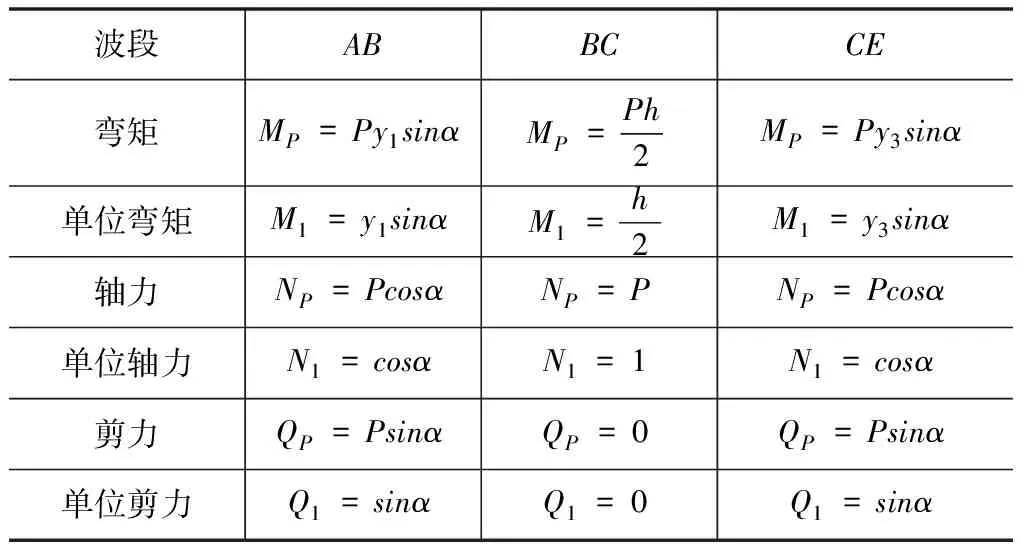
对于如图1所示的梯形波钢腹板，作用有x方向的轴向作用力P，由于直面BC段和斜面CE段的存在，其轴向变形相比于直钢板多出了弯矩和剪力引起的变形。以半个波形(BCE段)长度作为研究对象。通过单位力法按刚度等效原则计算波形钢板的等效厚度和等效弹性模量。轴向作用力P作用下，波形钢腹板各段单位宽度内的单位弯矩、单位轴力和单位剪力见表1。

根据单位力法，作用力P在半幅BCE段内产生的位移为：

图1 波形钢腹板示意

波段ABBCCE弯矩MP=Py1sinαMP=Ph2MP=Py3sinα单位弯矩M1=y1sinαM1=h2M1=y3sinα轴力NP=PcosαNP=PNP=Pcosα单位轴力N1=cosαN1=1N1=cosα剪力QP=PsinαQP=0QP=Psinα单位剪力Q1=sinαQ1=0Q1=sinα

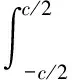
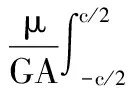
(1)

同理，长度为a+b、厚度为t′的等直钢板，在轴力P作用下产生的位移为：

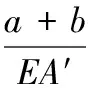
(2)

利用刚度等效原则，应有δ1=δ2。同时将A=t,A′=t′,I=t3/12,G=μE代入，则可得等效厚度t′和等效弹性模量E′：

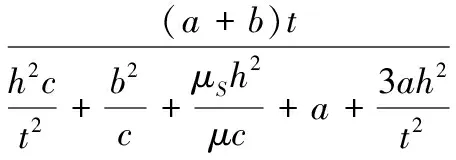
(3)

(4)

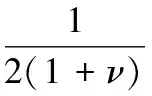
若忽略剪切力和轴力对斜板的影响，则公式可简化为：

(5)

(6)

如图2所示BCSW1600型波形钢腹板尺寸，以标准空腹段为例，t=16 mm代入式(5)，可得t′=0.00246t。

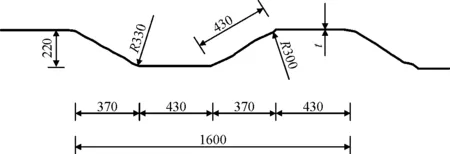
图2 BCSW1600型波形钢腹板

2 波形钢腹板刚度贡献定量分析

2.1 工程概况

郑州陇海路常庄干渠桥是国内第一座采用顶推法施工的波形钢腹板PC组合箱梁，采用波形腹板左右幅断面对称布置，施工现场见图3。波形钢腹板采用BCSW1600型，与混凝土顶板采用Twin-PBL方式连接，与混凝土底板采用S-PBL+栓钉连接，导梁采用现浇梁段波形钢腹板。

2.2 解析计算

为便于定性分析，解析计算时仅对波形钢腹板PC组合

图3 施工现场

箱梁桥在顶推过程中的内力变化进行分析。基本假定：(1)导梁与主梁完整地结合在一起；(2)导梁与主梁分别具有均一的自重荷载集度(分别为qs、q)和抗弯刚度(分别为EsIs、EI)；(3)主梁各跨跨径分别为li，导梁长度为ls；(4)忽略支座沉降以及施工误差等引起的次内力的影响；(5)波形钢腹板刚度按式(5)以等效厚度的等直钢板代入计算刚度。

以常庄干渠桥顶推工程实际参数进行计算：将主梁简化为均质梁，依据设计图纸和现场实际情况，综合考虑钢筋质量，取C60混凝土密度ρc=2.6×103kg/m3，重力加速度g=10 N/kg。依据设计图纸本次顶推段包括1个Ⅰ号段(27.5 m)和2个Ⅱ号段(50 m)，Ⅰ号段混凝土数量为255.1 m3，Ⅱ号段混凝土数量为425.7 m3，则混凝土总数量为425.7×2+255.1=1106.5 m3，标准段钢腹板总重量为188.2 t，所以主梁自重荷载q=(1106.5×2.6÷127.5+188.2)×10=263 kN/m。同理依据设计图纸和现场实际情况，将导梁简化为均质梁，导梁总重为175.7 t，则导梁自重荷载qs=175.7×10÷35=50 kN/m。

2.2.1 等效弯矩求解

依据力法及叠加原理，取多跨简支梁作为计算基本结构，将中间节点作为基本未知量(图4)。

图4 计算简图

图5 支反力计算

依据三弯矩方程有：

Mi - 1li+ 2Mi(li+li + 1) +Mi + 1li + 1=

(7)

式中：ωi代表左侧简支梁弯矩图的面积；ai代表形心Ci到支座i-1的距离；ωi+1代表左侧简支梁弯矩图的面积；bi代表形心Ci+1到支座i的距离。

依据式(7)建立方程组可求得支点处等效弯矩。

2.2.2 支反力求解

依据材料力学和结构力学原理，如图5所示，其支反力

满足如下公式：

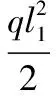
(8)

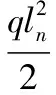
(9)

(10)

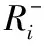
2.2.3 导梁挠度求解

导梁挠度计算示意图见图6。

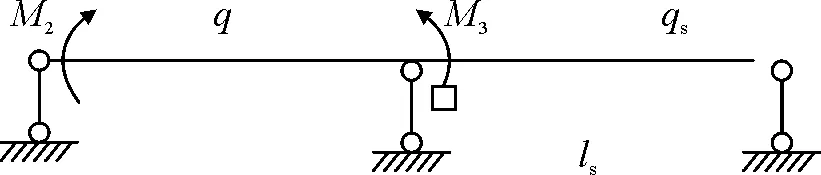
图6 导梁挠度计算示意

依据叠加原理悬臂端导梁挠度由两部分构成，包含3号支点处转角引起的挠度和悬臂端荷载引起的挠度。

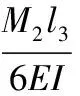
(11)

所以导梁悬臂端挠度为：

(12)

2.3 有限元计算

采用MIDAS Civil模拟整个顶推过程并进行仿真计算。将顶推施工中的结构离散成空间杆系模型，主梁和导梁均简化为空间梁单元，顶推平台和临时墩采用只受压的弹性支承来模拟。

2.3.1 截面模拟

主梁为波形钢腹板PC组合箱梁，考虑到波形钢腹板与顶、底板相比抗弯性能极小，在建立模型时忽略波形钢腹板的抗弯性能，仅考虑顶、底板的抗弯。波形钢腹板简化成2 cm的混凝土板以便截面输入，墩顶和标准断面如图7、图8所示。

图7 墩顶截面示意

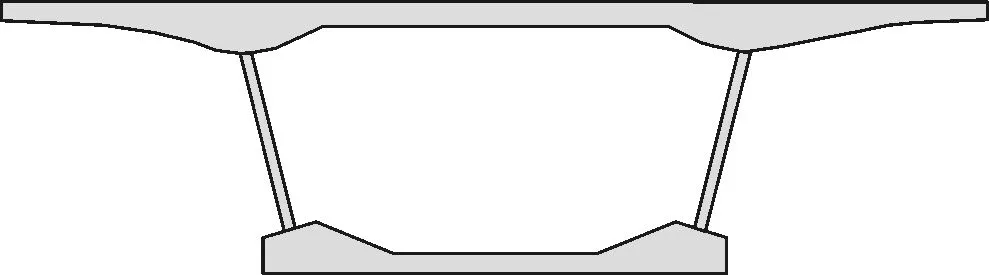
图8 标准断面示意

导梁中的波形钢腹板以直代曲，钢导梁末端取2倍钢腹板厚度，以工字梁模拟。导梁单元均为等截面形式，主要截面如图9、图10所示。

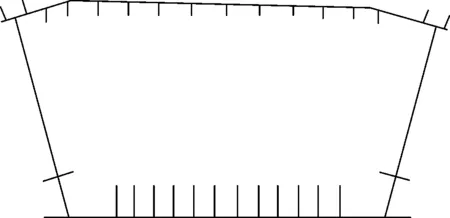
图9 导梁根部截面示意

图10 导梁标准段截面示意

2.3.2 施工阶段模拟

主要施工步骤见表2。

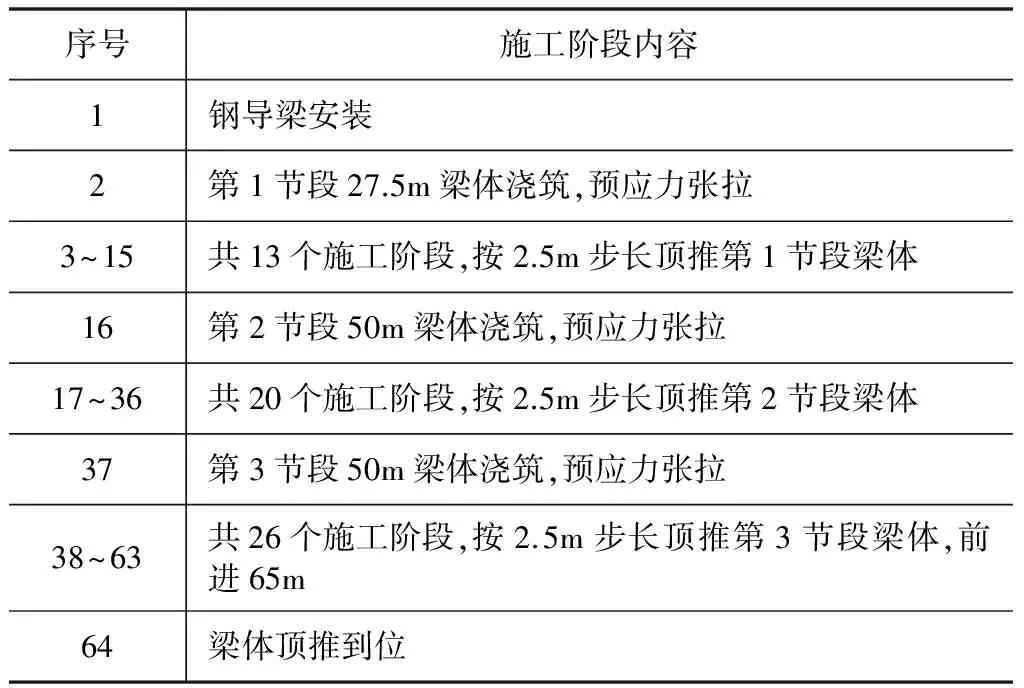
表2 顶推施工阶段工序

顶推过程的实现采用“墩动梁不动”计算模式，即主梁和导梁结构空间位置始终不变，通过边界条件后移来实现“向前顶推”，边界条件后移则是利用Midas里的激活和钝化边界条件功能。结构各单元及节点一次生成，且在整个计算中的位置和编号固定不变，不需要进行多次重新划分，根据顶推施工阶段的划分，将各支座依次后移，部分计算模型如图11所示。

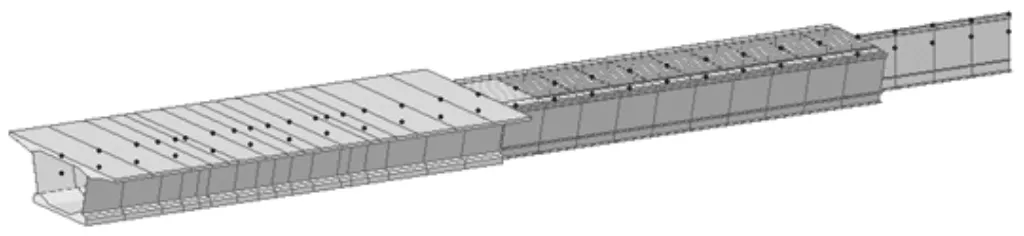
图11 部分计算模型

2.4 结果分析

现场监测断面布置及编号如图12、图13所示，有限元模型计算顶推过程中关键截面内力结果如表3所示。

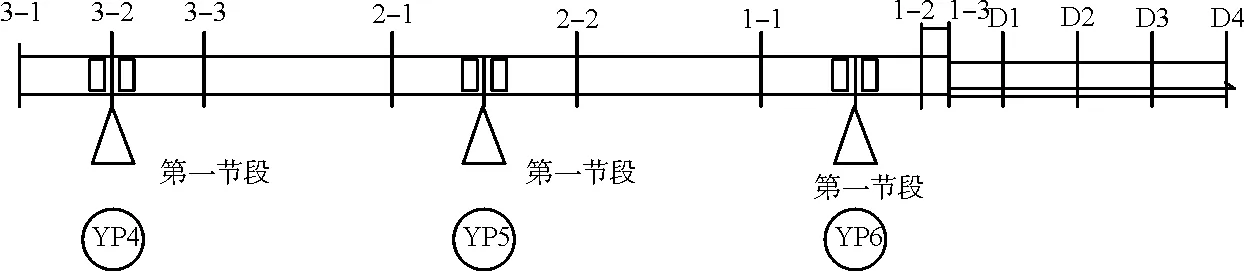
图12 变形监测断面示意

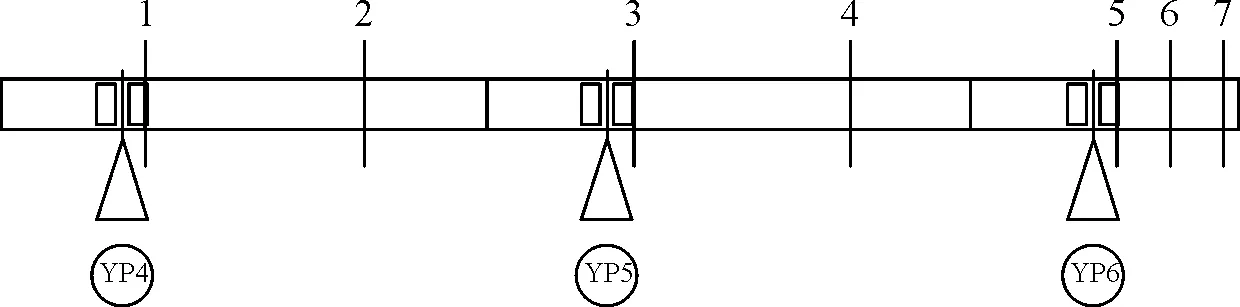
图13 应力监测断面示意

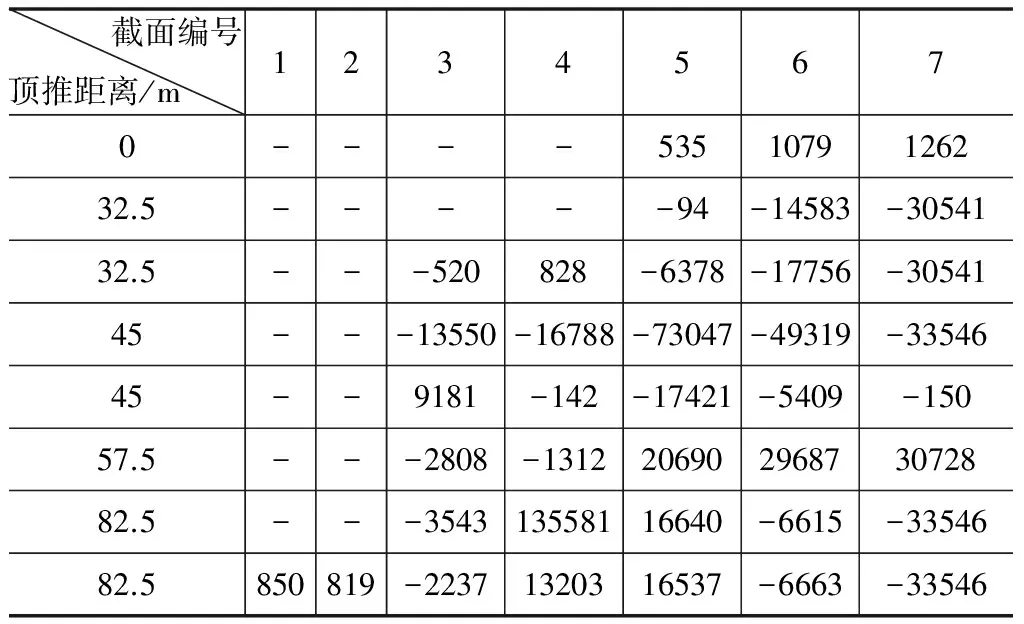
由表4可见，导梁前端实测挠度与解析计算和MIDAS数值模拟结果总体比较接近，解析计算总体偏小，平均偏差幅度小于15 %。解析计算挠度值与实测值偏差控制在-5 %～10 %之间。挠度整体规律表现为：数值模拟挠度值>实测挠度值>解析计算挠度值。由于解析计算时定量考虑波形钢腹板刚度贡献，而数值模拟时忽略其刚度，可见波形钢腹板刚度对导梁挠度有影响，同时考虑波形钢腹板刚度贡献的解析计算更接近实测值。

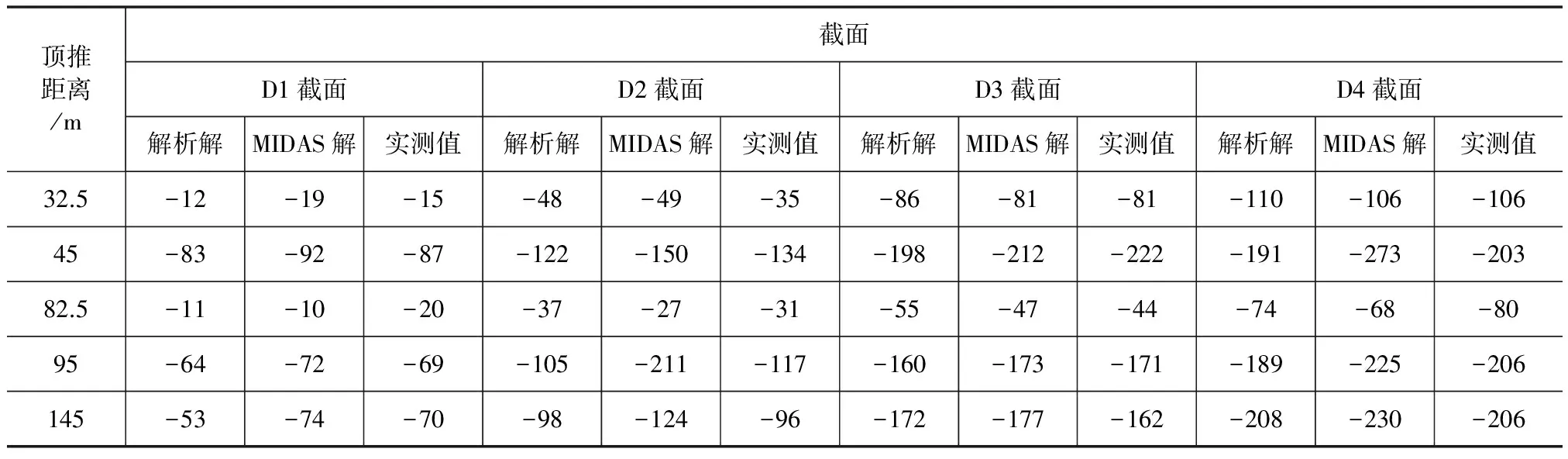
表4 导梁关键截面位移 mm

3 结论

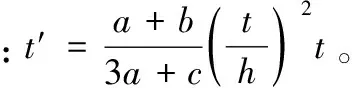
(2)通过考虑波形钢腹板刚度影响的解析法和不考虑其影响的数值模拟法分别计算郑州市陇海路常庄干渠桥导梁挠度并与现场实测挠度值对比，得出考虑波形钢腹板刚度贡献时更接近实测值。可见在波形钢腹板桥设计中采用等效厚度法计入波形钢腹板刚度贡献更符合实际工况。

[1] Mohamed Elgaaly , Anand Seshadri , Robert W. Hamilton. Bending strength of beams with corrugated webs[J].Journal of structural Engineer,1997,123(6):772-782.

[2] Machidamrong C, Watanabe E, Utsunomiys T. Analysis of corrugated steel web Girders by an efficient beam bending theory[J]. Structural Engineering and Earthquake Engineering, 2004,21(2):131-142.

[3] 李宏江,叶见曙,万水. 剪切变形对波形钢腹板箱梁挠度的影响[J]. 交通运输工程学报,2002(4):17-20.

[4] 苏俭,刘钊. 波形钢腹板箱梁桥考虑剪切变形影响的挠度计算方法[J]. 中外公路,2010(3):143-147.

[5] 刘保东,任红伟,李鹏飞. 考虑波纹钢腹板箱梁特点的挠度分析[J]. 中国铁道科学,2011(3):21-26.

[6] 聂建国,李法雄. 考虑腹板剪切行为的波形钢腹板梁理论模型[J]. 中国公路学报,2011(6):40-48.

[7] 聂建国,李法雄,樊健生. 波形钢腹板梁变形计算的有效刚度法[J]. 工程力学,2012(8):71-79.

[定稿日期]2017-07-26

陈钒(1972～)，男，硕士，高级工程师，主要从事桥梁结构研究、桥梁及结构理论分析、桥梁病害检测及性能评估、既有桥梁实时健康监控、桥梁特种施工工艺设计、高墩大跨桥梁施工监控、桥梁工程监理等方面的技术工作。

U443.32

A

材料力学公式得：