水激波管脉冲压力信号特性研究

陈威铮，徐春冬， 孔德仁， 顾廷伟， 赵 侃

(1. 南京理工大学 机械工程学院， 南京 210094； 2. 南京理工大学 工程训练中心， 南京 210094)

水激波管脉冲压力信号特性研究

陈威铮1，徐春冬1， 孔德仁1， 顾廷伟1， 赵 侃2

(1. 南京理工大学 机械工程学院， 南京 210094； 2. 南京理工大学 工程训练中心， 南京 210094)

为了更加科学合理地利用水激波管对水下冲击波压力测量系统进行动态校准， 对水激波管爆炸冲击波压力场影响因素进行了研究. 介绍了水激波管装置的基本结构及比对式校准原理， 利用AUTODYN有限元仿真软件对水激波管进行仿真， 根据数值仿真结果和相关系数相似度评定方法， 得出了水激波管爆炸冲击波形成稳定的平面波以及产生与实际水下爆炸工况相似的冲击波信号所需的长径比条件. 对仿真数据进行曲线拟合， 得出了水激波管内腔长度与装药量对脉冲压力峰值的影响关系式， 对水激波管的设计以及运用水激波管进行动态校准具有一定的指导意义.

水激波管； 水下冲击波； 爆炸压力测量

水下冲击波压力大小是评价各类水下武器系统的主要技术指标， 具有幅值高、 变化快、 测量环境恶劣等特点， 目前常采用压电式压力传感器对其进行测量. 压电式压力传感器的动态特性较好， 但是其低频特性较差， 难以通过静态校准的方式准确获得其灵敏度特性， 因此， 需对其进行动态校准. 目前， 水下冲击波压力测量系统的校准主要采用的是标准药柱法[1]， 该方法是根据药柱的质量及水下冲击波压力经验公式得出理论值并将其用于测量系统的动态校准， 由于水下爆炸的复杂性以及标准药柱的不确定性， 导致理论计算结果与实际情况出入较大， 校准精度难以保证. 针对目前国内水下冲击波压力测量系统校准方法存在的缺陷， 朱明武教授等[2-4]提出了基于水激波管的校准方法， 运用水激波管模拟水下冲击波压力的传递过程， 产生频率丰富的准δ脉冲， 用于水下冲击波压力测量系统的动态校准， 该方法在宫赤坤等[5]进行的校准实践中取得了不错的效果. 虽然水激波管在工程上已经有所应用， 但目前对于水激波管内复杂的压力场研究仍然较少， 仅依靠工程经验难以准确迅速获得理想的脉冲压力信号， 因此有必要对水激波管爆炸冲击波压力场特性及其相关影响因素进行深入研究.

本文采用AUTODYN有限元软件对TNT药柱在水激波管中的爆炸情况进行了仿真， 根据仿真结果得出了装药量与内腔长度对水激波管脉冲压力峰值的影响关系式.

1 水激波管装置及比对式校准原理

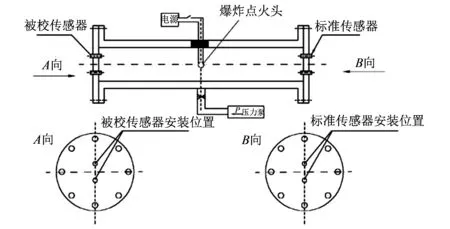
图 1 水激波管装置示意图Fig.1 Water shock tube device diagram

水激波管装置结构如图 1 所示. 水激波管是一个耐高压的对称结构， 爆炸点火头位于其几何中心， 将被校传感器与标准传感器分别对称安装在水激波管两端， 通过起爆控制系统引爆TNT药柱， 在水激波管中产生准δ脉冲压力信号， 该脉冲压力信号作为激励信号分别作用在标准压力传感器系统及被校水下冲击波压力测量系统， 采用比对式方法对被校冲击波压力测量系统进行动态校准. 预压加载系统通过专用螺纹接头与激波管腔体相连， 提供偏值压力， 模拟实际水压.

在运用水激波管进行动态校准时， 采用比对式方法对被校冲击波压力测量系统进行动态校准， 将被校冲击波压力传感器与标准压力传感器分别对称安装在水激波管两端的端面上， 采用齐平安装方式.

2 AUTODYN有限元仿真

2.1 无限水域模型

无限水域模型的材料选自软件内置材料库： 水介质采用Polynomial状态方程， TNT标准药柱采用JWL状态方程， 水介质和TNT药柱采用Euler网格， TNT的药量为0.12 g， 起爆方式为点起爆， 流固耦合方式为自动耦合， 无限水域为1/4二维简化模型， 边长为600 mm， 采用透射边界条件， 使得冲击波压力能够无反射地向外传播， 在水中施加1.5 MPa水压， 以模拟实际水下爆炸工况， 沿冲击波传递方向500 mm处设置高斯监测点1， 以监测冲击波压力波形. 图 2 为无限水域中TNT球形药柱爆炸所产生的冲击波波形与压力波形.

图 2 无限水域爆炸冲击波波形与压力波形Fig.2 Infinite water explosion shock waveform and pressure waveform

2.2 水激波管模型

水激波管模型的材料选自软件内置材料库： 水介质选用Polynomial状态方程， TNT标准药柱采用JWL状态方程， 水激波管腔体采用40CrNi2Mo高强度钢. 起爆方式为点起爆， 流固耦合方式为自动耦合.

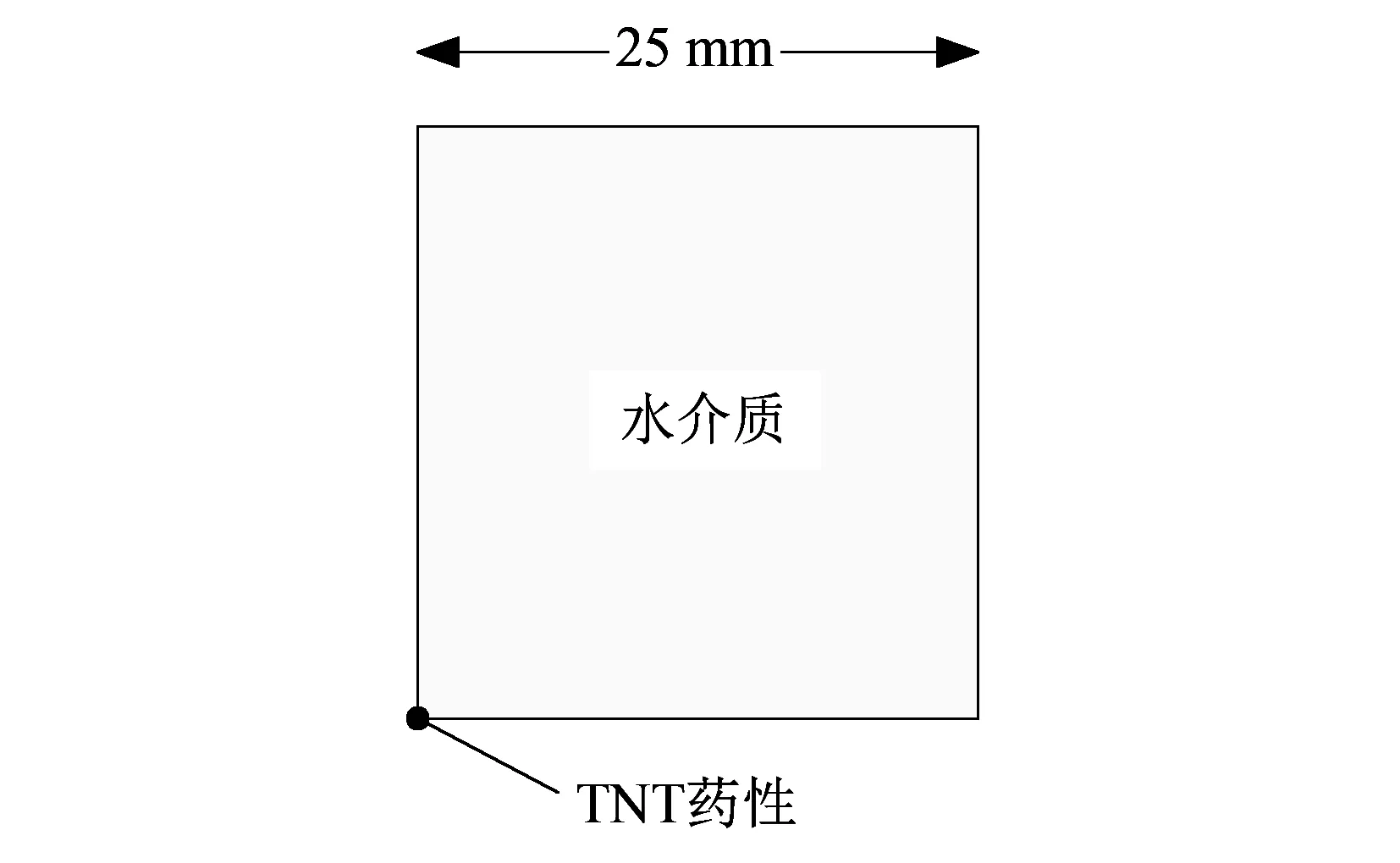
图 3 水激波管爆心简化模型Fig.3 Simplified water shock tube explosion center model

为了提高仿真精度， 在对水激波管中TNT标准药柱进行网格划分时， 需保证其网格单元足够小， 若将水激波管整体装置进行网格细分， 又会给计算机带来过大的运算量. 因此， 为了能够在保证仿真精度的同时， 减少计算机运算量， 现单独建立水激波管爆心模型. 采用AUTODYN建立1/4二维简化模型， 如图 3 所示. 水介质和TNT药柱采用Euler网格， 网格尺寸为0.05 mm×0.05 mm， TNT药柱为球形药柱且药量可调， 水域边长为25 mm， 水压为1.5 MPa， 为了使冲击波在水介质中能够无反射向外传播， 采用透射边界条件[6-10].

水激波管为1/4二维简化模型， 采用Lagrange网格进行划分， 网格尺寸为5 mm×5 mm， 内径取100 mm， 外径取200 mm， 水激波管内腔长度可调， 定义n为水激波管内腔长度和内径之比， 简称长径比，n取10， 12， 14， 16， 18， 20， 22， 24， 26， 28， 30， 32， 其简化模型如图 4 所示， 在图 4 所示的位置1与位置3处施加固定约束， 在位置2处施加透射边界条件， 在位置4与位置5处设置高斯监测点1和高斯监测点2， 设置水压为1.5 MPa. 仿真时， 将水激波管爆心简化模型带入水激波管模型. 图 5 为引爆标准药柱后， 水激波管内的爆炸冲击波压力云图.

图 4 水激波管简化模型Fig.4 Simplified water shock tube model

图5 水激波管内高斯监测点分布及爆炸冲击波压力云图Fig.5 The distribution of Gaussian monitoring points in water shock tube and explosive shock wave pressure cloud

2.3 水激波管平面波形成规律

利用水激波管产生的准δ信号对传感器进行动态校准时， 通常要求该激励信号为平面波， 当TNT药柱在水激波管内爆炸时， 爆炸所产生的冲击波将会以球面波的形式向四周扩散. 受壁面反射的影响， 水激波管中除了沿轴向传递的冲击波， 还将出现由管道四周壁面反射回来的各种状态的反射波， 它们在水激波管腔体内相互叠加， 传播一定距离后， 才能逐渐形成沿管道轴向传播的平面波.

为了确保实验校准精度， 到达水激波管端面的理想冲击波应为平面波， 并且波阵面最前端所在横截面上的压力值应保持一致， 因此需对爆炸后水激波管内冲击波的传播规律进行研究. 取最有代表性的高斯监测点1和高斯监测点2所监测的压力波形进行比较. 不同长径比n所对应的压力监测值的对比结果如图 6 所示.

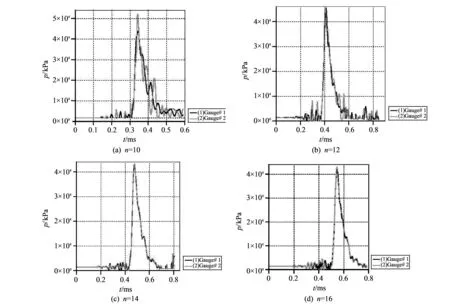
图 6 水激波管内腔端面冲击波压力波形Fig.6 The shock wave pressure waveform at the end of water shock tube inner cavity

由图 6 可知， 当n=10时， 水激波管内腔端面压力峰值由圆心向圆周方向逐渐衰减且圆心处压力峰值明显大于圆周处， 此外波形也存在较大差异； 当n=12与n=14时， 各点所监测的压力峰值接近且波形上升阶段高度吻合； 当n=16时， 各点所监测的压力峰值基本相同， 且波形在大部分时间内保持一致. 由此可以发现， 当长径比n大于14时， 爆炸所产生的冲击波将以平面波的形式传递到水激波管内腔端部， 并且长径比越大， 爆炸所产生的平面波波形越稳定.

3 准δ信号与实际工况下爆炸冲击波相似度分析

3.1 波形相似度评定方法

为了有效地利用水激波管产生的准信号对水下冲击波压力测量系统进行动态校准， 要求准δ信号能够近似地模拟实际水下工况的冲击波压力波形. 保持内径尺寸不变， 按照长径比为12， 16， 20， 24， 28， 32改变水激波管内腔的长度进行多组仿真， 将准信号与实际水下工况下的爆炸冲击波压力波形进行比较， 采用皮尔逊相关系数的方法进行相似度评定.

式中：r为两组数列x和y的相关系数， 取值范围为[-1,1]，r越大表明正相关程度越高.

在实际校准中， 起主要作用的是水下冲击波信号的上升沿部分. 因此， 首先对信号进行预处理， 取压力峰值从10%到100%的区间段作为水激波管准δ信号和实际水下工况冲击波压力信号的上升沿部分， 并将不同长径比条件下的准δ信号和实际水下工况爆炸冲击波信号的上升沿部分作为相似度分析的对象.

为了消除压力峰值和上升时间的不同对二者相似度的影响， 首先对压力幅值进行归一化操作， 使得压力幅值的范围在[0.1,1]； 其次， 保证信号具有相同的时间宽度， 具体方法为：

图 7 信号预处理流程Fig.7 Signal preprocessing flow

3.2 波形相似度与长径比的关系

将图 2 高斯监测点1监测所得的冲击波压力信号作为基准信号， 改变长径比， 将图5中高斯监测点2监测所得的冲击波压力信号作为被比较信号， 按照3.1节中所述方法对不同长径比条件下得到的水激波管准信号进行相似度分析， 计算结果如表 1 所示.

表 1 水激波管与无限水域冲击波波形相似度

从表 1 可知， 当水激波管长径比小于16时， 波形相似系数较低， 说明长径比过小时， 水激波管内无法产生稳定的且与实际水下工况爆炸冲击波相似的准δ信号. 当长径比大于16时， 波形相似系数稳步提升， 说明此时水激波管中产生的准δ信号与实际水下工况爆炸冲击波信号高度相似. 图 8 将实际水下工况、 长径比为12和长径比为16的3组条件下的冲击波信号进行对比， 长径比为16时的波形明显更接近实际水下工况， 而长径比为12时， 波形衰减振荡过大， 与实际工况差别较大， 不宜作为校准信号. 因此， 若想准δ信号的相似度高于90%且衰减振荡较小， 在水激波管尺寸设计时应保证其长径比不小于16.

图 8 水激波管内腔端面冲击波压力波形Fig.8 The shock wave pressure waveform at the end of water shock tube inner cavity

4 水激波管脉冲压力峰值的影响因素

4.1 水激波管内腔长度变化对脉冲压力峰值的影响

为了研究装药量和水激波管内腔长度对脉冲压力峰值的影响， 设置5组不同的装药量(g)， 以及9组不同的内腔长度(m)， 分别进行有限元仿真， 得到的压力峰值(MPa)仿真结果如表 2 所示.

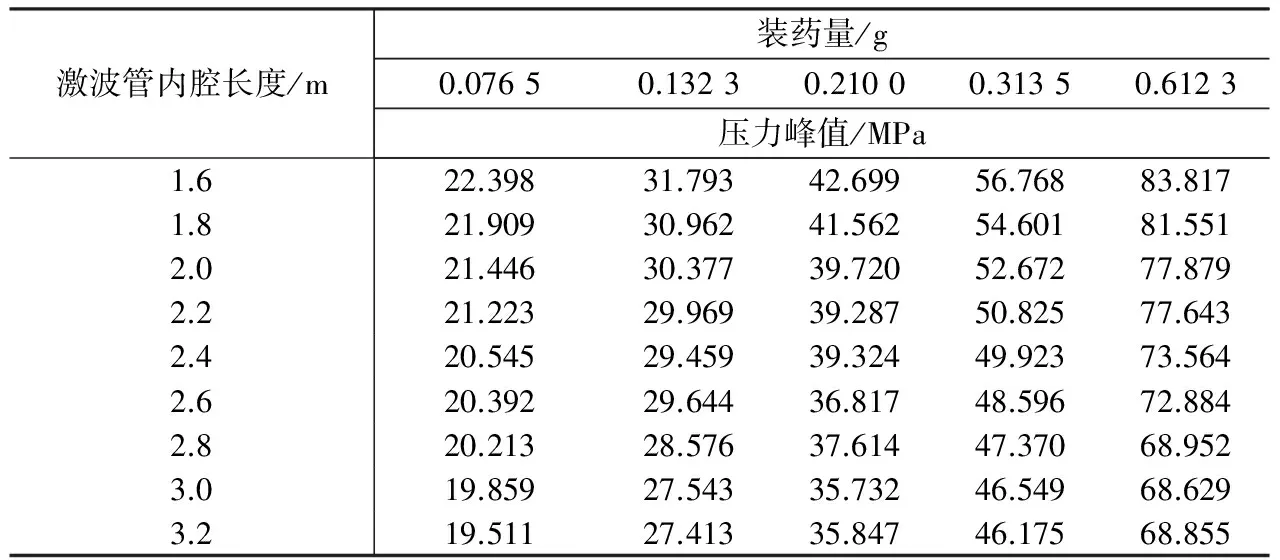
表 2 数值仿真结果

运用MATLAB对表 2 中数据进行曲线拟合， 并得到装药量一定时， 不同内腔长度对水激波管脉冲压力峰值的影响关系式. 定义y为压力值(MPa)，x为内腔长度(m)， 关系式以及曲线为： ① 装药量为0.076 5 g时，y=0.3796x2-3.573x+27.12， 拟合曲线如图9(a). ② 装药量为0.132 3 g时，y=0.272 7x2-4.034x+37.45， 拟合曲线如图9(b). ③ 装药量为0.210 0 g时，y=1.638x2-12.43x+58.51， 拟合曲线如图9(c). ④ 装药量为0.313 5 g时，y=2.745x2-19.795x+81.34， 拟合曲线如图9(d). ⑤ 装药量为0.612 3 g时，y=3.17x2-24.97x+115.8， 拟合曲线如图9(e). 可以发现， 当水激波管内径与装药量保持一定时， 随着水激波管内腔长度的增加， 到达水激波管端部的冲击波压力峰值逐渐衰减， 且衰减速率有所减小. 此外， 装药量越大， 随着水激波管内腔长度的增加， 冲击波压力峰值衰减越快.

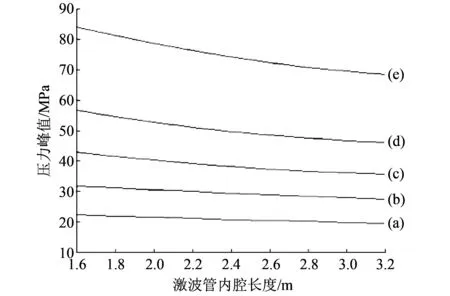
图 9 激波管内腔长度变化时冲击波压力峰值曲线Fig.9 Maximum value of shock wave pressure with change of the length of shock tube’s lumen

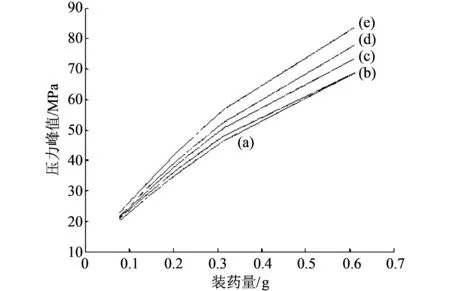
图 10 装药量变化时冲击波压力峰值曲线Fig.10 Maximum value of shock wave pressure with change of charge volume

4.2 水激波管装药量变化对脉冲压力峰值的影响

运用MATLAB对表2中数据进行曲线拟合， 并得到水激波管内腔长度一定时， 不同装药量对水激波管脉冲压力峰值的影响关系式. 定义y为压力(MPa)，x为装药量(g)， 关系式以及曲线为： ① 水激波管内腔长度为1.6 m时，y=-98.67x2+182.5x+9.093， 拟合曲线如图10(a). ② 水激波管内腔长度为2 m时，y=-84.35x2+163x+9.706， 拟合曲线如图10(b). ③ 水激波管内腔长度为2.4 m时，y=-87.89x2+158.3x+9.484， 拟合曲线如图10(c). ④ 水激波管内腔长度为2.8 m时，y=-82.88x2+146.9x+10， 拟合曲线如图10(d). ⑤ 水激波管内腔长度为3.2 m时，y=-68.93x2+138.7x+9.701， 拟合曲线如图10(e). 可以发现， 当水激波管内腔长度保持一定时， 随着装药量的增加， 到达水激波管端部的冲击波压力峰值逐渐增强， 且增长速率有所减小.

5 结 论

本文基于AUTODYN有限元仿真软件， 研究了爆炸冲击波在水激波管内的传播规律和波形参数， 得出了水激波管内平面波的形成条件， 即长径比不小于16； 利用相关系数的相似度评定方法， 得出了水激波管准信号和实际水下爆炸工况下冲击波信号的相似程度与长径比的关系， 即长径比不小于16时， 二者相似度高于90%； 通过仿真所得数据， 得出了水激波管压力峰值与装药量、 水激波管内腔长度的函数关系式.

综合全文可得出以下结论： ① 水激波管只需很少的药量即可产生较大压力峰值的准信号， 可有效节约试验成本； ② 为了能够形成理想的准信号， 用于水下冲击波压力测量系统动态校准的水激波管应满足长径比不小于16的基本条件； ③ 装药量较小时， 水激波管内腔长度对冲击波压力峰值的影响较小， 反之则越大； ④ 相同内腔长度的条件下， 改变装药量能够显著改变冲击波压力峰值.

本文对于了解水激波管爆炸冲击波的压力场特性， 指导水激波管外形尺寸及内部装药设计具有一定的参考意义.

[1] 马锦垠. 压电式压力传感器灵敏度标定方法研究[J]. 中国科技信息, 2012(7)： 125-125.

Ma Jinyin. Piezoelectric pressure sensor sensitivity calibration method research[J]. China Science and Technology Information, 2012(7)： 125-125. (in Chinese)

[2] 朱明武, 文小健. 高压动态标定用的水激波管[J]. 实验流体力学, 1993(3)： 43-46.

Zhu Mingwu, Wen Xiaojian. Physical vibration tube for high-pressure dynamic calibration[J]. Pneumatic Experiment and Measurement Control, 1993(3)： 43-46. (in Chinese)

[3] 朱明武, 李永新. 高压动态标定技术的进展[J]. 现代测量与实验室管理, 1996(1)： 37-41.

Zhu Mingwu, Li Yongxin. Progress in high-pressure dynamic calibration technology[J] .Journal of Test & Measurement, 1996(1)： 37-41. (in Chinese)

[4] 黄芬. 压力动态标准方法研究[D]. 南京： 南京理工大学, 2004.

[5] 宫赤坤, 李永新. 高压动态校准的水激波管[J]. 传感器与微系统, 2008, 27(5)： 61-63.

Gong Chikun, Li Yongxin. Water shock tube of high pressure dynamic calibration[J]. Transducer and Microsystems Technologies, 2008, 27(5)： 61-63. (in Chinese)

[6] 项大林, 荣吉利, 何轩, 等. 等效水下爆炸冲击加载装置的设计研究[J]. 兵工学报, 2014, 35(6)： 857-863.

Xiang Dalin, Rong Jili, He Xuan, et al. Development of an equivalent on underwater explosion impulsive loading[J]. Acta Armamentarii, 2014, 35(6)： 857-863. (in Chinese)

[7] 刘科种, 徐更光, 辛春亮, 等. AUTODYN水下爆炸数值模拟研究[J]. 爆破, 2009, 26(3)： 18-21.

Liu Kezhong, Xu Gengguang, Xin Chunliang, et al. Research on numerical simulation in underwater explosion by AUTODYN[J]. Blasting, 2009, 26(3)： 18-21. (in Chinese)

[8] 徐豫新, 王树山, 李园. 水下爆炸数值仿真研究[J]. 弹箭与制导学报, 2009, 29(6)： 95-97.

Xu Yuxin, Wang Shushan, LiYuan. Study on numerical simulation of the underwater explosive[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2009, 29(6)： 95-97. (in Chinese)

[9] 贾宪振, 王建灵, 高赞, 等. 有限水域水中爆炸气泡脉动的数值模拟[J]. 舰船科学技术, 2015, 37(8)： 31-34.

Jia Xianzhen, Wang Jianling, Gao Zan, et al. Numerical simulation of bubble pulse of underwaterexplosion in confined water area[J]. Ship Science and Technology, 2015, 37(8)： 31-34. (in Chinese)

[10] 方斌, 朱锡, 张振华, 等. 水下爆炸冲击波数值模拟中的参数影响[J]. 哈尔滨工程大学学报, 2005, 26(4)： 419-424.

Fang Bin, Zhu Xi, Zhang Zhenhua, et al. Effect of parameters in numerical simulationof underwater shock wave[J]. Journal of Harbin Engineering University, 2005, 26(4)： 419-424. (in Chinese)

StudyonCharacteristicsofPulsePressureSignalofWaterShockTube

CHEN Weizheng1, XU Chundong1, KONG Deren1, GU Tingwei1, ZHAO Kan2

(1. School of Mechanical Engineering, Nanjing University of Science and Technology， Nanjing 210094, China; 2. Engineering Training Centre, Nanjing University of Science and Technology， Nanjing 210094, China)

In order to use the water shock tube to dynamically calibrate the underwater shock wave pressure measurement system scientifically and rationally, the influencing factors of the shock wave pressure field of the water shock tube are studied. This paper introduced the basic structure of the water shock tube device and the principle of alignment calibration. The simulation of the water shock tube is carried out by using the AUTODYN finite element simulation software. According to the numerical simulation results and the correlation coefficient similarity evaluation method, the required ratio of the shock wave for water shock tube which can form a stable plane wave and generate a shock wave signal similar to the actual underwater explosion condition is obtained. By curving fitting the simulation data. The relationship of pulse pressure peak between the length of the water shock tube cavity and the charge volume is obtained, the relationship has some guiding significance for the design of water shock tube and the dynamic calibration of water shock tube.

water shock tube; under water shock wave; explosion pressure measure

1671-7449(2017)06-0524-07

2017-04-11

陈威铮(1992-)， 男， 硕士生， 主要从事水下冲击波压力传感系统校准方法的研究.

TP212

A

10.3969/j.issn.1671-7449.2017.06.010