尾矿坝属性参数概率分布类型及变化趋势研究

张飞飞， 杨风暴， 王肖霞

(中北大学 信息与通信工程学院， 山西 太原 030051)

尾矿坝属性参数概率分布类型及变化趋势研究

张飞飞， 杨风暴， 王肖霞

(中北大学 信息与通信工程学院， 山西 太原 030051)

现有研究认为大多数坝体属性参数服从中心极限分布， 但由于属性参数实际取值范围有限， 导致采用中心极限分布不足以表征参数的非正态分布特性， 造成所拟合分布模型与实际参数分布区间契合度低等问题. 考虑到坝体属性参数具有非负值， 且存在偏度， 首先用“3σ”准则结合样本数据的偏度确定样本分布取值范围； 根据参数偏度特征利用改进的经典分布拟合法拟合出不同分布概率密度曲线和累积概率函数曲线， 从而对参数概率分布模型进行推断， 并根据卡方检验法、 K-S检验法进行检验； 在确定参数分布类型后， 利用曼-肯德尔法对参数变化趋势作出分析. 研究结果表明： 固结排水剪切试验中粘聚力分布取值表现出左偏态特征， 其他实验下参数取值均表现出右偏态； 固结排水剪切和不排水剪切实验中粘聚力服从极值I型分布， 内摩擦角服从对数正态分布； 固结不排水剪切实验中粘聚力和内摩擦角均服从正态分布； 固结排水剪切和不排水剪切实验中粘聚力在经历波动期后均表现出下降趋势， 而3组实验中内摩擦角整体在经历波动期后均呈现显著上升趋势.

尾矿坝； 属性参数； 偏度； 概率分布； 经典分布拟合

在进行尾矿坝稳定性分析时， 筑坝材料属性参数概率分布类型的不同将造成稳定性分析结果产生较大的偏差， 有效建立属性参数的最优概率分布类型， 是获得精确稳定性分析结果的前提. 如刘志伟等[1-3]研究发现： 尾矿抗剪强度参数取不同的概率分布时， 造成结构工程可靠度计算结果最大相差10倍以上. 尾矿坝属性参数粘聚力(c)和内摩擦角(φ)作为结构工程稳定性分析的重要因素， 其取值区间和分布类型直接关系到坝体的风险评价. 很多学者进行了大量研究确定其最优分布类型. 如苏卫卫等[4]通过利用K-S法对土体抗剪强度指标的概率分布类型进行统计， 认为c服从正态分布，φ服从对数正态分布； 岩小明[5]通过对边坡抗剪强度参数c,φ进行统计分析， 发现c服从对数正态分布，φ服从正态分布； 郑轶轶等[6,7]人研究软土力学参数的分布规律， 认为抗剪强度参数均服从正态分布； 而宫凤强等[8]人认为岩土参数服从正态信息扩散分布.

在上述研究中， 均假设岩土属性参数服从若干有限统计分布， 并采用检验方法确定不同参数最优分布类型为正态分布或对数正态分布. 但在使用正态分布进行坝坡稳定性分析时， 意味着参数可以取负值， 这与实际参数的取值区间不符. 姚晨辉等[9,10]人认为坝坡属性参数并非严格服从正态分布， 可能表现出正偏态或负偏态分布， 优先使用对数正态分布更为合理. 然而使用对数正态分布表征参数的分布虽避免了坝坡属性参数取值区间左端出现负值的情况， 但任何属性参数右端的取值范围也是有限的. 同时， 实际坝坡工程中的属性参数并未表现出严格服从中心极限分布， 利用正态或对数正态分布拟合参数的分布类型， 一定程度上导致实际属性参数分布表征的局限性.

基于以上问题， 本文在考虑实际属性参数取值范围的基础上， 根据“3σ”准则， 在考虑样本数据偏度系数的情况下， 确定属性参数的实际取值区间. 然后结合参数的偏度特征改进经典分布拟合中分布函数参数值的确定， 由此对参数进行统计分析研究， 对属性参数的最优概率分布类型进行推断， 并通过两种检验法验证该方法的合理性. 另外在确定参数最佳分布类型后， 采用曼-肯德尔法对参数总体的变化趋势进行分析.

1 尾矿坝属性参数定量描述

土体属性参数粘聚力和内摩擦角是岩土结构工程变形与稳定性分析的关键指标， 如尾矿坝风险评估、 边坡可靠性分析等. 本文选取3组土体属性参数粘聚力和内摩擦角的实验数据作为样本数据[11]， 这3组实验数据分别为： 63组3轴固结排水剪切试验数据(CD)、 64组固结不排水剪切试验(CU)和61组3轴不排水剪切试验(UU).

尾矿坝稳定性分析中， 考虑到属性参数的非负性、 实验误差等因素影响， 首先对原始实验数据进行预处理. 本文在考虑实际参数具有一定偏度的基础上， 采用“3σ”准则剔除异常数据， 确定样本数据实际取值范围. 具体取值区间由式(1)～式(3)确定：

当l>0时

当l<0时

当xmin≤0时

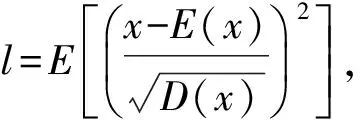
以3组实验数据为研究对象， 利用上述方法对其进行预处理， 确定坝体属性参数的实际取值分布范围， 为进一步探究不同实验情况下不同属性参数的分布奠定基础. 如表 1 为样本数据分布取值范围.

表 1 样本数据分布取值范围

从表 1 中可以看出， 3组实验下的样本数据均具有一定的偏度， 并不严格服从正态分布. 其中3轴固结排水剪切试验数据中粘聚力表现出左偏态， 根据“3σ”准则， 其左端点取值为0； 其他样本数据表现出右偏态， 表明概率密度曲线的右尾巴长， 顶点偏向左边. 同时， 预处理中CD和CU实验中c和UU实验中φ的左端点均出现负值， 根据实际情况， 将其确定为0， 使样本数据的取值更为合理.

2 属性参数概率分布的确定

在确定各属性参数的分布取值范围后， 根据其取值范围特征(样本数据呈左偏态或右偏态)， 通过样本数据， 利用参数估计法(本文选取最大似然估计法)确定不同概率分布中属性参数分布函数X的参数值.

经典分布拟合法是用于确定与样本数据拟合程度最佳的分布形式. 依据有关随机变量物理知识和已有数据的统计特征， 本文选取对数正态分布、 极值I型分布、 正态分布、 瑞利分布和威布尔分布对数据进行拟合. 针对每种分布类型， 改进经典分布拟合法， 在已知样本数据具有一定偏态的基础上， 使用最大似然估计法确定最佳的分布参数， 并采用3种检验法对其拟合优度进行检验. 主要步骤为： ① 依据样本数据表现出的特征(左偏态或右偏态)， 对不同分布类型的分布密度f(x;θ)进行调整； ② 利用最大似然估计法估计分布密度f(x;θ)中的最佳参数值； ③ 依据相应分布的参数值画出各自概率密度曲线、 经验分布函数曲线和累积分布曲线图， 并进行比较， 初步推断出最佳分布类型； ④ 用卡方检验、 K-S检验比较所有拟合分布的检验结果， 拟合优度最小的为最佳分布； ⑤ 求取不同分布检验统计量的观测值， 并与临界值进行比较， 验证最佳分布的合理性.

2.1 最大似然估计法

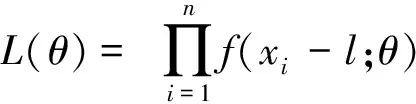
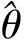
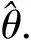
2.2 分布拟合结果对比分析

通过左偏态或右偏态的最大似然估计法， 可获得各分布的最佳拟合参数， 利用其值画出不同分布在各属性参数取值范围内的分布曲线， 借助拟合优度来衡量每种分布的拟合优劣. 选取两种检验法对拟合分布优度进行检验： 卡方检验法、 K-S检验法. 为具体分析每种拟合分布的特点及优劣， 分别从经典分布拟合的分布曲线、 检验值和累积概率值进行对比分析.

2.2.1 拟合分布曲线比较

对3组实验中的尾矿坝属性参数使用经典分布拟合法， 分别画出各分布拟合的情况. 图 1 给出了3组实验中属性参数的概率密度函数曲线和累积概率分布曲线.

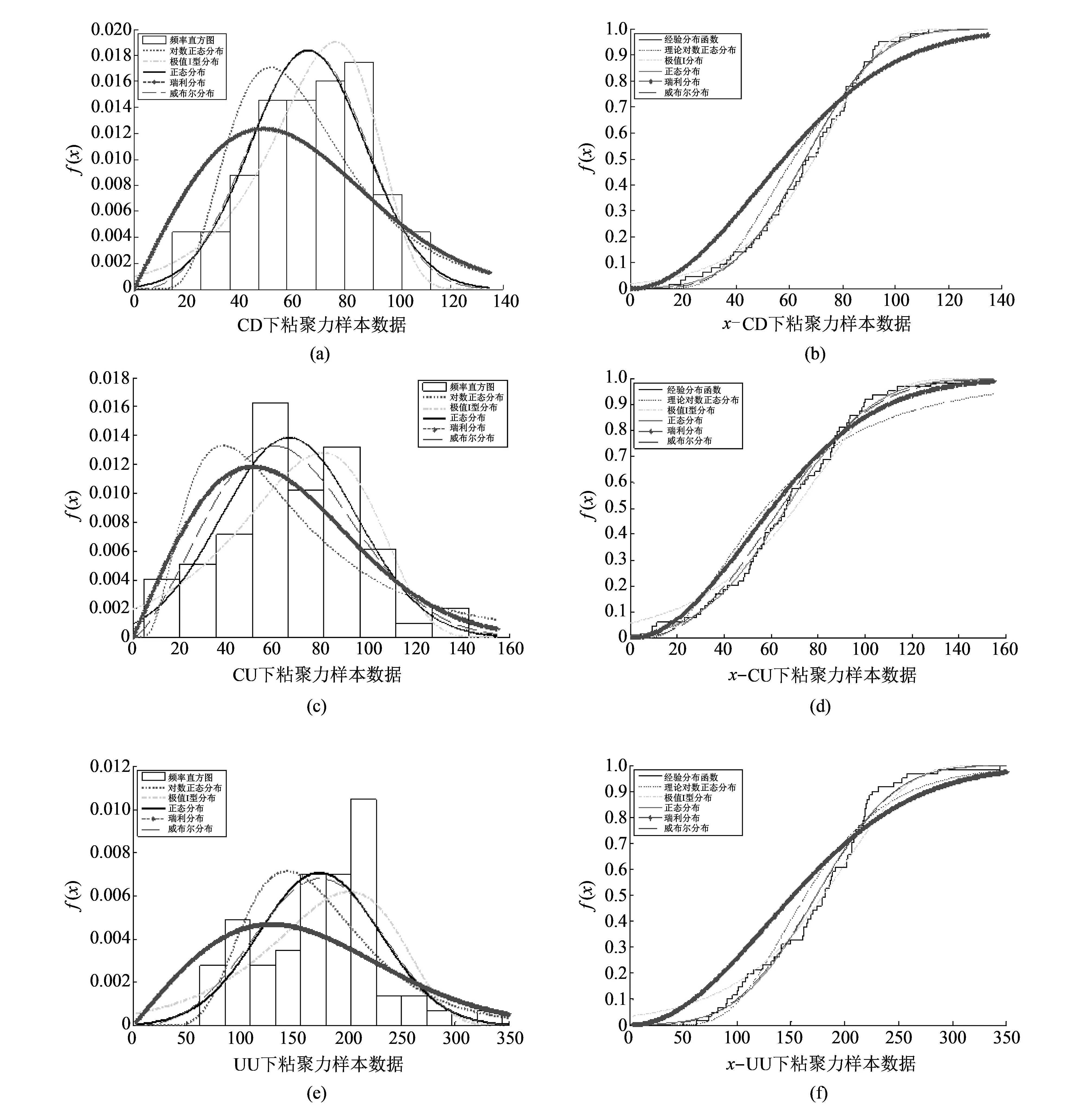
图 1 3组实验中的概率密度函数曲线和累积概率分布曲线Fig.1 The probability density function curve and cumulative probability distribution curve in three groups

从图 1 可看出， 3组样本数据中粘聚力取值主要集中在中间范围， 且存在一定波动， 整体表现出峰值前单调递增， 峰值后单调递减趋势， 因而采用单峰型分布进行拟合具有一定优势. 利用左偏态或右偏态的最大似然估计法对5种分布概率密度函数曲线的峰值点随样本数据进行一定调整， 使其可以随着样本的波动呈现不同的峰值改变. 通过概率密度函数曲线比较可发现： ① 图1(a)中CD下在分布取值范围内， 表现出了左偏态特征， 峰值点偏向右边， 5种分布中极值I型分布拟合效果较好， 且贴近实际取值. 同时在图1(b)中极值I型分布的累积分布函数曲线与样本数据的分布函数曲线契合度更高， 故推断CD实验下c服从极值I型分布； ② 图1(c)中CU实验c表现出右偏态特征， 但偏度不明显， 可以看出5种分布中正态分布拟合效果较优， 且正态分布在累积分布曲线中契合度也最好， 故推断CU实验下c服从正态分布； ③ 图1(e)中UU实验在取值区间内， 表现出峰值前缓慢递增， 峰值后迅速递减的特征， 在5种拟合分布中， 正态分布和极值I型分布拟合效果较好， 正态分布在整体上拟合了样本数据， 但数据的趋势未凸显出来， 极值I型分布峰值前缓慢递增， 峰值后骤减， 更符合实际数据分布变化趋势， 逼近程度更高， 故推断UU实验下c服从极值I型分布.

对3组实验下的尾矿坝属性参数φ使用经典分布拟合法， 图 2 给出了3组实验中φ的概率密度函数曲线和累积概率分布曲线.

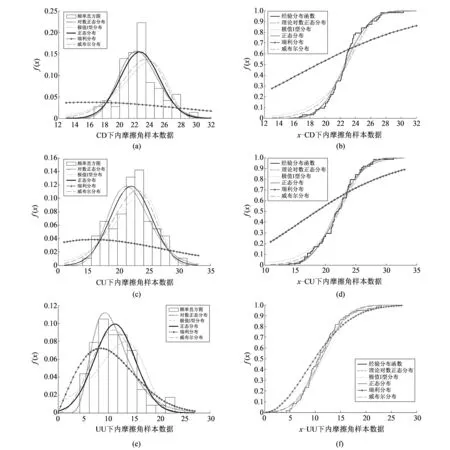
图 2 3组实验中φ的概率密度函数曲线和累积概率分布曲线Fig.2 The φ probability density function curve and cumulative probability distribution curve in three groups

从图 2 中可以发现： 3组实验中φ的分布取值范围较小， 且瑞利分布对其拟合效果最差， 不适用于对小范围样本数据的拟合. 3组摩擦角样本数据峰值点均集中于中间范围， CD和CU实验下的样本数据峰值左右变化趋势较显著， UU实验下样本数据表现出较明显的右偏态， 峰值左侧变化趋势较大， 右侧相对较缓. 通过比较两类曲线可以发现： ① 图2(a)中CD下的φ在分布取值范围内， 峰值偏向于左端， 表现出不明显的右偏态， 且数据右尾巴较长， 5种分布中对数正态分布拟合效果较优， 故推断CD实验下的φ服从对数正态分布； ② 图2(c)中CU下的φ峰值左侧表现出迅速递增， 峰值右侧表现出迅速递减， 正态分布拟合曲线随数据波动性变化最为明显， 且累积分布函数曲线中也呈现出最优拟合特性， 故认为CU下的φ服从正态分布； ③ 图2(e)中UU下的φ呈现出较明显的右偏态特征， 比较各分布拟合曲线， 对数分布拟合效果最优， 图2(f)中也验证了对数正态分布的合理性， 故推断UU下的φ服从对数正态分布.

2.2.2 检验值和累积概率值比较

本文选取卡方检验、 K-S检验进行检验， 当检验的P值小于或等于显著性水平α(取0.05)时， 拒绝该分布的拟合假设， 否则接受原假设拟合分布. 其中通过P值检验的分布， 检验值(统计量)需小于临界值， 且检验值越小则其拟合精度越高. 表 2 和表5 给 出了两种检验法下3组实验c和φ的各分布检验的P值表. 表 3 和表 6 给出了3组实验c和φ的卡方检验结果， 表 4 和表 7 为3组实验c和φ的各分布K-S检验结果. 表 8 为3组实验c和φ的各分布累积概率值.

表 2 两种检验法下c的不同分布检验的P值表

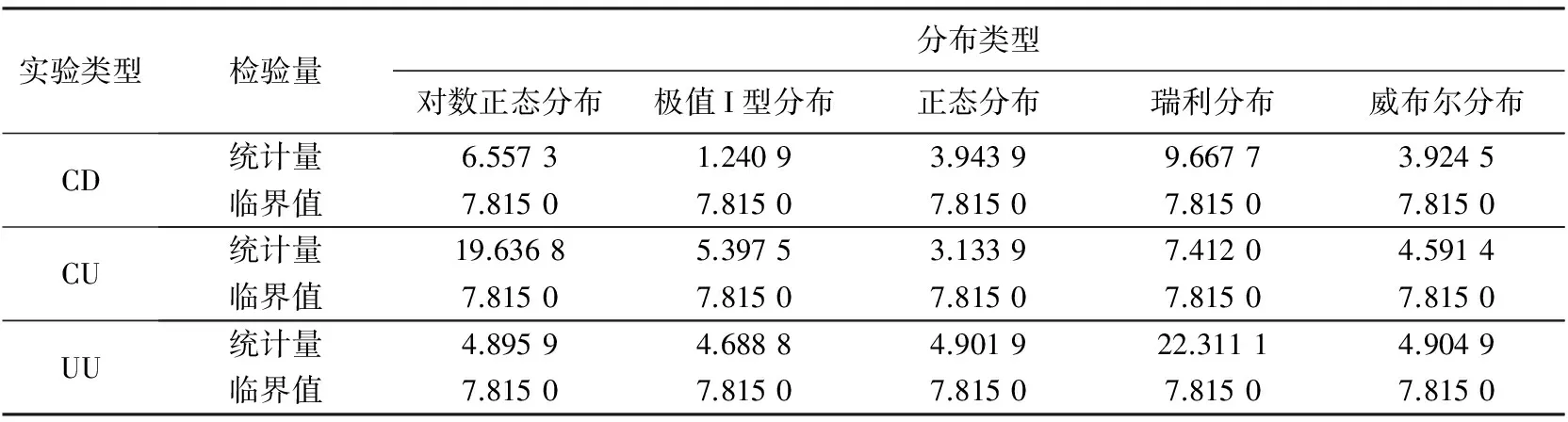
表 3 粘聚力c的卡方检验结果

表 4 粘聚力c的K-S检验结果

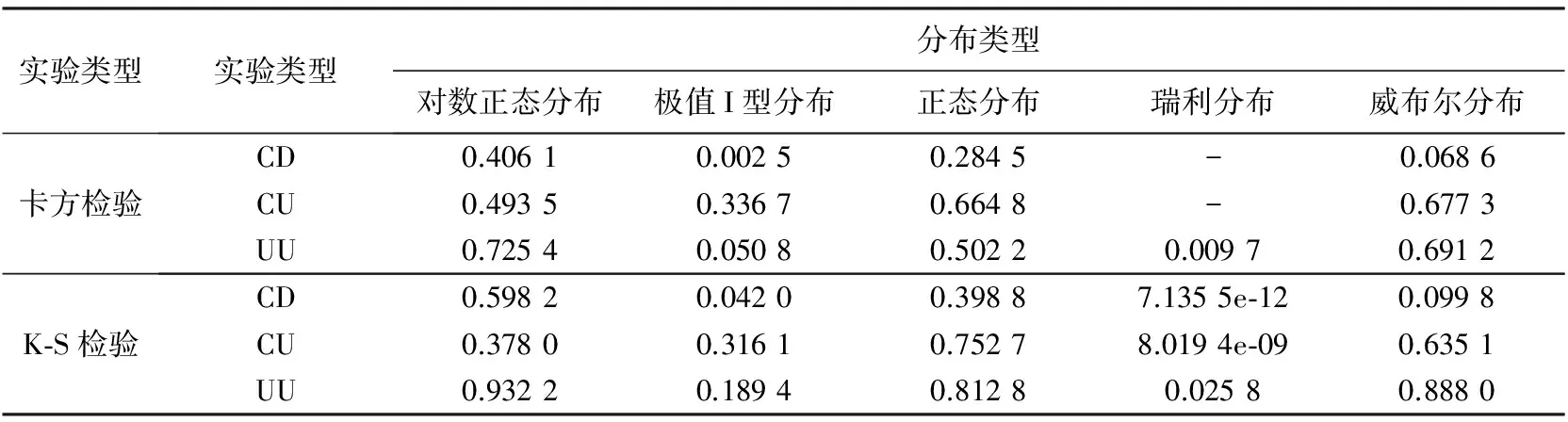
表 5 两种检验法下φ的不同分布检验的P值表

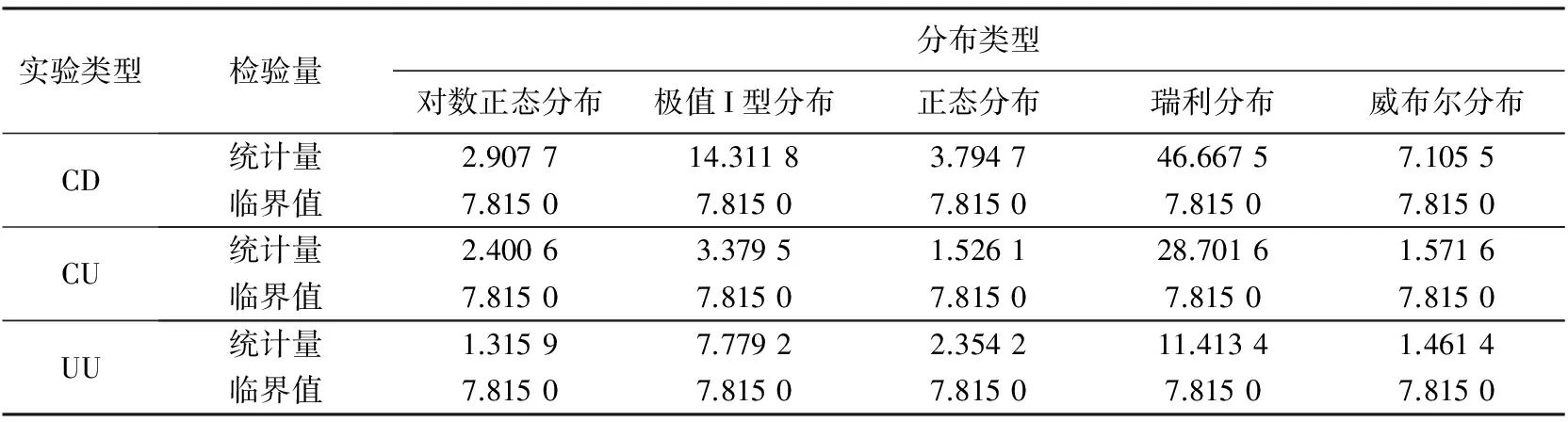
表 6 内摩擦角φ的卡方检验结果

表 7 内摩擦角φ的K-S检验结果

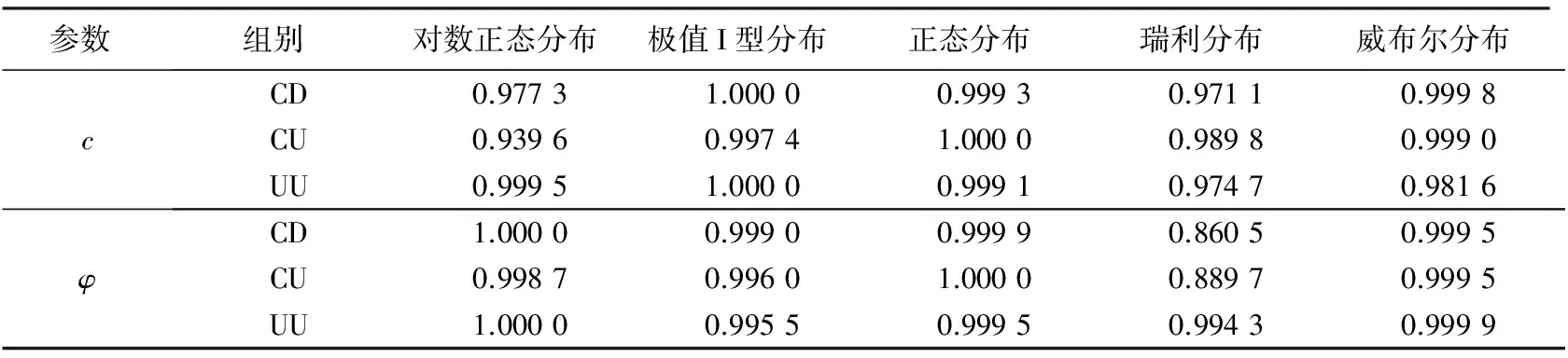
表 8 3组实验c和φ的各分布累积概率值

由表 2 可知， CD实验下c的5种拟合分布中， 除瑞利分布检验P值大于显著性水平外， 其余分布检验P值均小于显著性水平， 即通过了检验. 通过检验的4种分布中， 表3中CD实验下检验值大小排序为对数正态分布>正态分布>威布尔分布>极值I型分布， 因而极值I型分布是CD实验下c最佳拟合分布， 表4中K-S检验量和表8中c的累积概率值进一步证明了该结论. 同理可得， CU实验下c的拟合分布通过检验的检验值大小排序为瑞利分布>极值I型分布>威布尔分布>正态分布， 故正态分布是CU实验下c最佳拟合分布； UU实验下c的拟合分布通过检验的检验值大小排序为威布尔分布>正态分布>对数正态分布>极值I型分布， 故极值I型分布是UU实验下c的最佳拟合分布.

同样表5中， CD实验下φ的5种拟合分布中， 除极值I型分布和瑞利分布检验的P值大于显著性水平外， 其余分布P值均小于显著性水平， 即通过检验. 表6中CD实验下通过检验的3种分布中， 检验统计量大小排序为威布尔分布>正态分布>对数正态分布， 因而对数正态分布是CD实验下φ的最佳拟合分布， 表7中K-S检验量和表8中φ的累积概率值进一步证明了该结论. 同理可得到CD， CU， UU实验下φ的最优分布分别为对数正态分布、 正态分布和对数正态分布. 与文献[11]相比， 本文考虑参数偏态特征对拟合分布参数进行最大似然估计， 所得拟合分布对样本数据的趋势变化更合理， 分布拟合更贴近实际.

3 属性参数变化趋势分析

根据属性参数某一阶段分布特征来估计下一阶段参数的变化趋势， 进而推断坝体稳定性变化， 是对尾矿坝进行有效加固、 科学治理的前提. 为此， 本文在3组实验中某一阶段对参数连续监测的基础上， 根据不同实验下参数服从的最优分布， 利用曼-肯德尔法对参数的变化做出预测， 以期为参数趋势变化研究提供直接依据.

在UBk和UFk的曲线图中， 若UFk值大于0， 则表明序列呈上升趋势； 小于0为下降趋势； 当其超过临界值时， 表明上升或下降趋势显著； 如UBk和UFk在临界线内相交， 则交点为突变开始时间.

图 3 3组实验下粘聚力变化趋势图Fig.3 Trend diagram of cohesion change in three groups

在图3(a)中， 粘聚力整体表现出上升趋势，UBk和UFk计算值均在临界值范围内波动， 因而CD下的粘聚力变化趋势不显著， 在第60个样本数据之后逐渐出现下降趋势； 图3(b)中， CU下的粘聚力波动性较强， 变化趋势比较复杂， 在监测期内UBk和UFk有10次突变， 均围绕在统计值0上下波动， 相对持平； 图3(c)中， UU下的粘聚力在第30个数据之前， 样本整体呈上升趋势， 之后表现出下降现象， 且在第57个样本达到显著性水平.

在图4(a)中， CD下的内摩擦角在第52个监测值之前整体为下降趋势， 之后开始上升， 且达到了突变水平， 在第60个监测值时超过临界值， 上升趋势显著； 图4(b)中， CU下的内摩擦角在第35个监测值之前样本值基本持平， 之后持续上升并达到显著性水平； 图4(c)中，UU下的内摩擦角表现出先上升后下降， 在第37个监测值后持续上升. 3组实验下的内摩擦角表现出相同的特征， 在经历一段波动后都出现上升的趋势.

图 4 3组实验下内摩擦角变化趋势图Fig.4 Trend diagram of internal friction angle in three groups

4 结 论

在探究尾矿坝属性参数概率分布的方法中， 一般的中心极限分布方法存在与参数分布区间契合度低， 无法真实反映参数的趋势变化， 并且累积概率值小于1的问题. 针对目前经典分布拟合中的5种分布， 在考虑属性参数取值非负且取值范围有限的基础上， 提出采用带有偏度的“3σ”准则方法确定参数分布取值区间. 在此基础上， 对5种分布拟合方法进行系统比较， 研究结论如下：

1) 现有分布拟合存在忽视属性参数分布取值范围特征， 拟合精度低等问题， 为此提出考虑参数取值偏态特征进行分布拟合的方法. CD实验下粘聚力的分布取值表现出左偏态特征， CU和UU实验下粘聚力均呈现出右偏态特性； CD, CU, UU实验下内摩擦角分布取值均表现出右偏态， 表明概率分布曲线的右尾巴长， 顶点偏向左边.

2) CD和UU实验下粘聚力最佳概率分布是极值I型分布， 传统的中心极限分布对其拟合精度低， 不适用于其变化趋势的描述. 极值I型分布更能凸显粘聚力趋势变化细节信息， 表征参数非正态分布特性； CU实验下粘聚力服从正态分布， 其偏态特征不显著.

3) CD和UU实验下内摩擦角最佳概率分布为对数正态分布， 其取值右偏态特征明显， 故分布曲线右尾巴长， 对数正态分布描述其分布变化更合理. CU实验下内摩擦角服从正态分布， 其取值在峰值左右变化趋势较接近.

4) CD下的粘聚力在第60个监测值前表现出上升现象， 之后开始下降； UU下的粘聚力在第30个监测值之前出现短暂上升， 之后表现出显著下降趋势， 在未来监测期内可能会持续下降. 3组实验下内摩擦角整体变化较一致， 均为在监测期内某监测值点之前上下波动， 之后整体均表现出显著上升趋势， 未来可能会持续上升.

[1] 王肖霞， 杨风暴. 诱导有序的基本信任分配及其在坝体风险评估中的应用[J]. 应用基础与科学工程， 2014(4)： 830-839.

Wang Xiaoxia， Yang Fengbao. A method of inducing ordered basic belief assignment and its application in risk assessment of tailing dam[J]. Journal of Basic Science And Engineering， 2014(4)： 830-839. (in Chinese)

[2] 刘志伟. 土体强度参数对边坡隧道影响数值模拟分析[J]. 水利与建筑工程学报， 2014(4)： 176-180.

Liu Zhiwei. Numerical stimulation analysis for the effects of soil mass strength parameters on the tunnels with side slopes[J]. Water Conservancy and Building Engineering， 2014(4)： 176-180. (in Chinese)

[3] Fan W， Li X， Hu G. Study on determining of reinforced concrete false roof strength and design of reinforcement based on reliability theory[J]. Engineering Sciences， 2012， 10(5)： 65-70.

[4] 苏卫卫， 黄宏伟， 张洁. 上海软粘土抗剪强度指标概率分布类型研究[J]. 地下空间与工程学报， 2012， 8(a2)： 1695-1699.

Su Weiwei， Huang Hongwei， Zhang Jie. Risk analysis of the underground passage through rail transit construction scheme[J]. Journal of Underground Space and Engineering， 2012， 8(a2)： 1695-1699. (in Chinese)

[5] 岩小明. 基于可靠度理论的露天矿边坡风险分析[D]. 长沙： 中南大学， 2013.

[6] 郑轶轶， 朱剑锋， 刘干斌， 等. 宁波软土物理力学参数概率分布及相关性研究[J]. 中国科技论文， 2013， 8(5)： 367-373.

Zheng Yiyi ， Zhu Jianfeng， LiuGanbin ， et al. Probability and correlation between physical and mechanical parameters of soft clays in Ningbo rail transit engineering[J]. China science and technology papers， 2013， 8(5)： 367-373. (in Chinese)

[7] Li D Q， Tang X S， Phoon K K. Bootstrap method for characterizing the effect of uncertainty in shear strength parameters on slope reliability[J]. Reliability Engineering & System Safety， 2015， 140： 99-106.

[8] 宫凤强， 黄天朗， 李夕兵. 岩土参数最优概率分布推断方法及判别准则的研究[J]. 岩石力学与工程学报， 2016， 35(12)： 2452-2460.

Gong Fengqiang， Huang Tianlang， Li Xibing. Research on approximation method and discriminative criterion of the optimal probability distribution of geotechnical parameters[J]. Journal of rock mechanics and engineering. 2016， 35(12)： 2452-2460. (in Chinese)

[9] 姚晨辉， 魏江波， 任光明， 等. 考虑岩土体参数变异性的滑坡破坏概率分析[J]. 水利与建筑工程学报， 2016， 14(2)： 100-103.

Yao Chenhui， Wei Jiangbo， Ren Guangming， et al. The failure probability analysis of landslide considering variability of soil parameters[J]. Water conservancy and building engineering， 2016， 14(2)： 100-103. (in Chinese)

[10] Wu X Z. Trivariate analysis of soil ranking-correlated characteristics and its application to probabilistic stability assessments in geotechnical engineering problems[J]. Soils & Foundations， 2013， 53(4)： 540-556.

[11] 张蕾， 唐小松， 李典庆. 基于Copula函数的土体抗剪强度参数二维分布模型[J]. 土木工程与管理学报， 2013， 30(2)： 11-17.

Zhang Lei， Tang Xiaosong， Li Dianqing. Bivariate distribution model of soil shear strength parameter using copula[J]. Journal of Civil Engineering and Management， 2013， 30(2)： 11-17. (in Chinese)

[12] 毛天宇， 戴明新， 彭士涛， 等. 近10年渤海湾重金属(Cu， Zn， Pb， Cd， Hg)污染时空变化趋势分析[J]. 天津大学学报(自然科学与工程技术版)， 2009， 42(9)： 817-825.

Mao Tianyu， Dai Mingxin， Peng Shitao， et al. Temporal-spatial variation trend analysis of heavy metals (Cu， Zn， Pb， Cd， Hg)in bohai bay in 10 years[J]. Journal of Tianjin University， 2009， 42(9)： 817-825. (in Chinese)

TheResearchontheProbabilityDistributionTypeandChangeTrendofTailingsDamAttributeParameters

ZHANG Feifei, YANG Fengbao,WANG Xiaoxia

(Information and Communication Engineering College, North University of China, Taiyuan 030051, China)

The existing studies think that most of the tailings dam attribute parameter obey central limit distribution. But the actual property parameter scope is limited, which cause problems that central limit distribution is not enough to characterize the non-normal distribution characteristics of the parameters and low fit is produced between fitting distribution model and the distribution interval of the actual parameters. Considering that the dam attribute parameters have nonnegative values and there is skewness, the value scope of sample distribution is determined by using the " " standards with the skewness of sample data.; Different probability density curve and cumulative probability function curve are fitted by the typical distribution fitting method on the basis of parameter skewness characteristics. The probability distribution model of the parameters are inferred and tested by the chi-squared and K-S test. After determining parameter distribution types, attribute parameter variation trend analysis is made by Man-Kendall method. The result shows that the cohesive force distribution of consolidation drained shear tests showed left skewness values of characteristics, while others showed right skewness. The cohesive force obeys the extreme 1-type distribution and the internal friction angle obeys logarithmic normal distribution in consolidated drained shear and undrained shear experiment. Cohesive force and internal friction angle are distributed to normal distribution in consolidated undrained shear experiment. The cohesive force in both consolidated drained shear and undrained shear experiment showed a downward trend after the period of fluctuation. However, the overall internal friction angle of the three groups showed a significant upward trend after the period of fluctuation.

tailings dam; attribute parameter; skewness; probability distribution; classical distribution fitting

1671-7449(2017)06-0469-10

2017-03-11

国家自然科学基金青年基金资助项目(61503345)； 山西省回国留学人员科研资助项目(2015-081)； 中北大学科学研究基金资助项目(110246)； 山西省研究生教育创新资助项目(2017181)

张飞飞(1993-)， 男， 硕士生， 主要从事信号与信息处理、 安全评估等研究.

TP391.9

A

10.3969/j.issn.1671-7449.2017.06.002