玻璃焊带直线检测算法研究

刘 凡， 张 权， 刘 祎， 赵 明， 桂志国,2

(1. 电子测试技术国家重点实验室(中北大学)， 山西 太原 030051；2. 仪器科学与动态测试教育部重点实验室(中北大学)， 山西 太原 030051)

玻璃焊带直线检测算法研究

刘 凡1， 张 权1， 刘 祎1， 赵 明1， 桂志国1,2

(1. 电子测试技术国家重点实验室(中北大学)， 山西 太原 030051；2. 仪器科学与动态测试教育部重点实验室(中北大学)， 山西 太原 030051)

为了实现工业上玻璃焊带高效、 高精度的自动切割， 提出了一种投影梯度法(Projection Gradient Method, PGM)： 新方法首先将待检测的原图像进行模板匹配， 获得一个待检测直线区域的子图像， 再将子图像在垂直方向进行投影， 获得灰度投影向量并求梯度得到灰度投影梯度向量， 然后将子图像围绕中心旋转， 当待检测直线与投影方向平行的时候， 投影梯度向量的极大值是最大的， 再根据图像的旋转和平移变换可求出待检测直线的方程. 实验结果表明： 梯度投影法能够满足玻璃焊带实时检测切割的要求.

玻璃焊带; 模板匹配; 子图像; 图像旋转; 直线检测

在玻璃焊带实际检测切割过程中， 直线检测的技术尤为关键. Hough变换是检测直线最常用的方法之一. 但是Hough变换运算量大、 速度慢， 不满足实时检测的需求. 文献[1]提出了一种改进的Hough变换LSD算法， 该算法用于局部提取直线， 虽然时间复杂度底， 但是由于局部检测算法自增长的特点， 对于长线段被遮挡、 局部模糊等情况经常会被分裂成多条直线. 文献[2]采用直线拟合的方法进行直线检测， 能够快速检测出边缘直线， 但是该算法受噪声影响较大， 特别是边缘不平整的情况下将严重影响检测精度. 针对Hough变换存在效率低下， LSD快速直线检测存在局部算法的缺点； 直线拟合算法没有较强的抗干扰能力， 本文提出了一种新的直线检测算法——投影梯度法. 该方法首先对待检测的直线区域进行模板匹配， 对匹配得到子图像在垂直方向投影并求梯度得到投影梯度向量； 然后将子图像按一定的小角度步长围绕中心旋转， 当投影梯度向量的极大值取得最大值时， 待检测的直线方向是垂直的.

1 玻璃焊带检测切割的基本流程

图 1 给出了玻璃焊带检测切割的流程[3-4]. 图1(a)中， 玻璃4边外侧的白色区域为银层； 图1(b)中， 上下黑色的矩形为焊带. 具体的流程为： ① 对于图1(a)， 检测左边和右边银层的外侧边缘直线， 记录检测的偏移值； ② 对于图1(b)， 在上下银层水平方向上自动放置焊带， 根据第一步检测的偏移值， 对放上去焊带进行切割， 图1(c)是图1(b)焊带切割好之后顺时针旋转90°的效果图； ③ 对于图1(c)， 检测左右两边焊带的内侧边缘直线， 记录其检测的偏移值. ④ 对于图1(c)在上下银层水平方向上自动放置焊带， 根据第③步检测的偏移值， 对焊带进行切割， 图1(d)是最终焊带切割完成的效果图. 最终使玻璃4周的银层上都有焊带， 形成了一个回字型的密闭空间， 为真空玻璃的封边奠定了基础.

图 1 玻璃焊带的切割示意图Fig.1 Schematic image of glass welding strip cutting

图 2 是玻璃焊带检测切割过程中用相机采集的原始图像. 图2白色的亮区域为玻璃上的银层， 图2(c) 银层上面的灰色长矩形是焊带. 图2(a)待检测直线与垂直方向平行； 图2(b)待检测的直线与垂直方向有一定的夹角； 图2(c)待检测焊带内侧边缘直线平行于垂直方向.

图 2 玻璃边角的原始图像Fig.2 The original image of the glass edge angle

2 检测的原理与算法

在实际检测切割过程中， 由于焊带是自动放在水平银层上面的， 对于玻璃无焊带图像， 切割刀是根据水平银层与垂直银层外侧边缘交线的偏移值进行切割； 对于玻璃有焊带图像， 切割刀是根据水平银层与焊带内侧边缘交线偏移值进行切割. 因此， 为了排除背景的干扰， 提高算法的精度， 以及减少银层上面的孔洞划痕等影响， 本文算法第一步采用模板匹配[5-7]， 对待检测的直线进行定位； 第二步对于模板匹配定位出来的子图像， 再使用投影梯度法来对直线进行检测. 针对玻璃无焊带的原始图像， 具体阐述本文的算法.

2.1 模板匹配

模板匹配就是在一幅大图像中搜索小图像， 大图像中有要找的目标， 且该目标同模板图像有相同的大小与方向， 通过一定的算法可以在图中定位到目标， 确定其坐标位置[8-10]. 本文从向量相关角度实现图像匹配. 对于大小为M×N的图像f(x,y)和大小为J×K的子图像模板w(x,y)， 将子图像w(x,y)认为是一个按行或按列存储的向量b， 将计算过程中被w(x,y)覆盖的图像区域视为按另一个按照相同方式存储的向量a. 两个向量之间的点积为

由于相关响应存在着对f(x,y)和w(x,y)的灰度幅值相对敏感的缺陷. 可以通过对向量乘积归一化解决这个问题. 通过式(2)来计算.

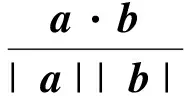
如图 3 是归一化相关匹配法的效果图.

图 3 归一化相关匹配法的效果图Fig.3 Result image of normalized correlation matching method

图3(a)～(d)分别是玻璃无焊带的原始图像， 图3(e)是模板图像， 模板图像是从玻璃无焊带的原始图像中截取待检测直线的区域. 图3(f)～(i)分别对应图3(a)～(d)归一化相关匹配法的效果图. 图3(f)～(i) 中黑色矩形是根据图3(e)模板匹配定位出来的区域.

从图3(f)～(e)匹配效果图中可以看出， 即使玻璃视野在图像中移动， 待检测直线有一定倾斜角度， 图像背景的差异和玻璃银层上有氧化等情况， 归一化相关匹配法能够克服背景环境等干扰， 准确地定位直线检测的区域， 具有很好的匹配效果.

2.2 投影梯度法

基于投影梯度法是把二维的图像灰度像素值投影变换成一维的数据， 再在一维数据的基础上进行梯度运算. 投影示意图如图 4 所示.

图 4 投影示意图Fig.4 The diagram of projection

其中s为投影方向，t为其垂直方向， 则图像函数f(x,y)沿着s的投影定义为

当θ固定时，p为t的函数.θ不断在0到2π之间变换， 可以得到在不同方向上的投影， 特别地， 当θ为0°和90°时， 在x,y轴上的投影分别为

本文针对玻璃无焊带图像模板匹配出来的子图像， 从垂直方向进行投影[12]， 设投影图像的宽度和高度分别为W,H.i，j分别为图像的第i行和第j列，f(i,j)为这一点的灰度像素值. 设为在图像垂直方向上对每列进行投影得到的投影向量：S=[S0,S1,…,Sj,…,SW-1]. 其中

对于投影向量S, 将相邻两项投影值进行后向差分运算， 得到一个投影梯度向量D=[S0-S1,S1-S2,…,Sj-1-Sj,…,SW-2-SW-1].

1) 图像待检测直线方向平行于投影方向

如果模板匹配出来的子图像的待检测直线方向平行于投影方向， 沿着垂直方向上投影， 该直线被投影成一个点， 则该直线在其对应投影点在梯度向量中的梯度值将呈现极大值[13]. 搜索此极值在梯度向量中的位置就可以知道图像中沿此方向的直线表达式. 图 5 是投影向量和投影梯度向量波形图.

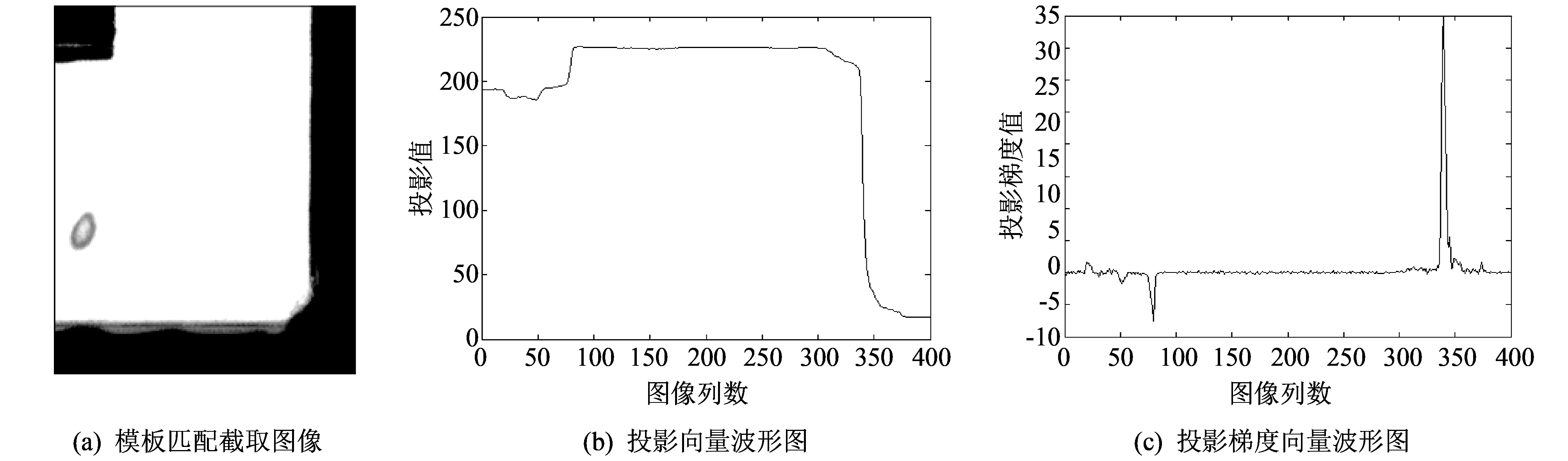
图 5 投影向量和投影梯度向量的波形图Fig.5 The waveform of projection vectors and projected gradient vectors

图5(a)是对原始图像通过模板匹配定位截取出来的子图像， 图像中要检测直线方向平行于投影方向， 图5(b)是投影向量的波形图， 横坐标表示投影图像每一列， 纵坐标表示投影向量元素的平均值， 即S/H, 其中S为投影向量，H为投影图像的高度. 图5(c)为投影梯度向量的波形图.

2) 图像上要检测的直线方向不平行于投影方向

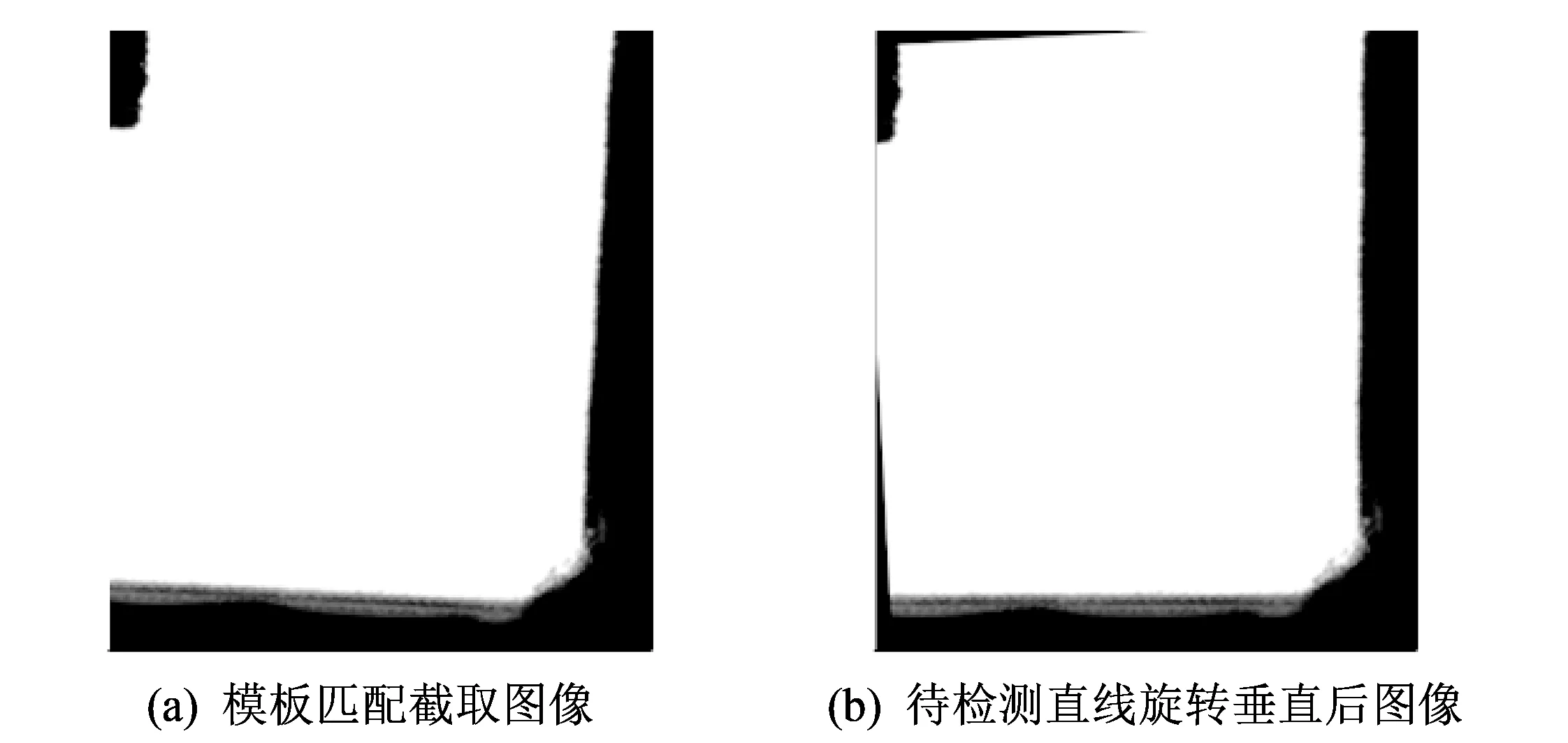
图 6 旋转效果图Fig.6 The diagram of rotate

如果模板匹配出来的子图像的待检测直线方向不平行于投影方向， 沿着垂直方向上投影， 该直线被投影成一条小线段. 设Dmax为投影梯度向量D中元素的最大值. 将模板匹配的子图像以小角度步长围绕图像中心旋转， 每旋转一个角度， 都有一个Dmax, 分别记为Dmax1,Dmax2,…,Dmaxk， 定义投影梯度最大值向量G[Dmax1,Dmax2,…,Dmaxk]. 随着图像的旋转， 待检测直线沿垂直方向上投影下来的线段越来越短， 其投影梯度向量的最大值越来越大， 随着待检测的直线方向逐渐旋转到平行于投影方向， 直线的投影将从线段逐渐缩小为一个点. 当投影梯度最大值向量G取得最大值Gmax时， 图像中待检测的直线也就旋转到垂直方向. 图 6 是旋转效果图. 图6(a)是对原始玻璃无焊带图像(图3(d))模板匹配定位截取出来的子图像， 图6(b)是将待检测直线旋转至垂直方向的图像.

通过投影梯度法， 可以得到图6(a)到图6(b) 沿中心旋转的角度θ， 以及图6(b)待检测直线的表达式， 设为x=R， 在x=R上任取两点(0,R), (h,R)， 假设匹配定位截取出来的图像宽度和高度分别为w,h. 匹配出来的区域的左上角坐标点在原始图像中为(m,n).

点(x0,y0)围绕图像坐标原点(0,0)转θ角度后坐标为(x1,y1). 则

文中对模板匹配截取后的子图像旋转是围绕图像中心进行的， 则先要将坐标系平移到中心点， 再进行图像的旋转， 然后平移到坐标原点[14-16]. 则图像的旋转公式为

其逆预算为

将图6(b)中在x=R直线上的两点(0,R), (h,r)带入式(8)， 可以得到图6(a)中待检测直线上两个点坐标， 再经过平移变化， 将图6(a)中的两个点转换为图3(d)中两个点的坐标， 设为(X1,Y1), (X2,Y2)， 则

在图6(b)上求出的表达式直线上取两点， 通过图像的旋转和平移变换， 可以求出原始图像中待检测直线的两点坐标， 即可知道原始图像中待检测直线的表达式. 因此， 对于一幅原始待检测直线图像， 首先通过模板匹配， 定位到待检测直线的区域， 得到模板匹配子图像， 然后进行图像旋转， 再根据图像投影梯度的极大值即可求出待检测直线的表达式.

3 实验结果与分析

此次实验所采用的照片是在玻璃焊带实时切割过程中用相机采集的. 实验是运用Visual Studio 2012结合Opencv 3.0编写出来的程序在Windows 7系统下进行的. 图 7 选取了3组不同类型的玻璃焊带图像用来作为实验结果的对比分析. 图 7 是PGM， Hough变换和LSD检测的效果对比图.

图 7 检测效果图Fig.7 The result image of detection

图7(a)和图7(e)的待检测直线是具有一定夹角的玻璃无焊带的原始图像、 图7(i)的待检测直线是具有一定夹角玻璃有焊带的原始图像. 投影梯度法的检测结果如图7(d)、 图7(h)和图7(l)所示， 已将所检测出来的直线用白线绘制在图上(下同). 图7(b)、 图7(f)和图7(j)是传统Hough变换检测的效果图， 其中图7(b)、 图7(f)、 图7(j)累加平面的阈值参数分别为165,295,145. 图7(c)、 图7(g)和图7(k) 为LSD快速直线检测的效果图.

梯度投影法没有经过任何的边缘提取和滤波等处理， 从图7(d)、 图7(h)和图7(l)的检测结果可以看出， 梯度投影法能够准确地检测玻璃焊带边缘直线. 传统的Hough变换虽然能够检测到待检测的直线， 从图7(b)、 图7(f)和图7(j)检测的效果图中可以看出， 累加平面阈值参数选取过大， 则检测不到待检测的直线， 累加平面阈值参数选取过小， 则会检测到图像中其它的直线. 因此， Hough变换很难选取一个阈值， 能够适应所有的检测情况， 检测的结果受到阈值选取的严重影响. 虽然LSD算法在检测过程中不依赖于参数， 更适合进行自动检测并且检测的速度较快， 能在短时间内获得亚像素级的结果. 但是由于LSD快速直线检测存在局部算法的缺点， 从而会导致检测到多条不相干的直线. 从图7(c)、 图7(g)和图7(k) 经过LSD直线检测的效果图中可以看出， 检测出来的直线会出现断裂， 图像中直线段的数量非常多.

与Hough变换相比， 梯度投影法不需要事先提取边缘点， 就能直接进行直线检测. 由于省去了边缘点的提取过程， 即可提高直线检测的速度； 梯度投影法也不需要对阈值进行事先的确定， 就能直接对直线进行检测， 可以避免传统方法中由于累加平面阈值选取不恰当所带来的直线检测误差.

与LSD快速直线检测算法相比， 梯度投影法具有很强的抗干扰能力， 尽管玻璃银层有些氧化， 以及银层上有孔洞划痕等一些背景的干扰， 梯度投影法都能正确的检测到待检测的直线. 而LSD快速直线检测算法会检测到许多其它短线段， 导致误检， 不能够满足玻璃焊带图像实时检测切割的工业要求.

表 1 是实际玻璃焊带切割过程中机械臂的偏移值与梯度投影直线检测算法偏移值的对比. 表1中单位均为mm. 偏差Δx是机械臂实际移动距离， 偏差Δy是算法检测到的偏差值， 误差d=Δy-Δx. 通过机械臂实际移动的距离与算法检测移动距离做对比， 可以检测算法的精度. 从表 1 中可以看出误差|d|<0.1 mm， 满足工业玻璃焊带切割的实际要求.

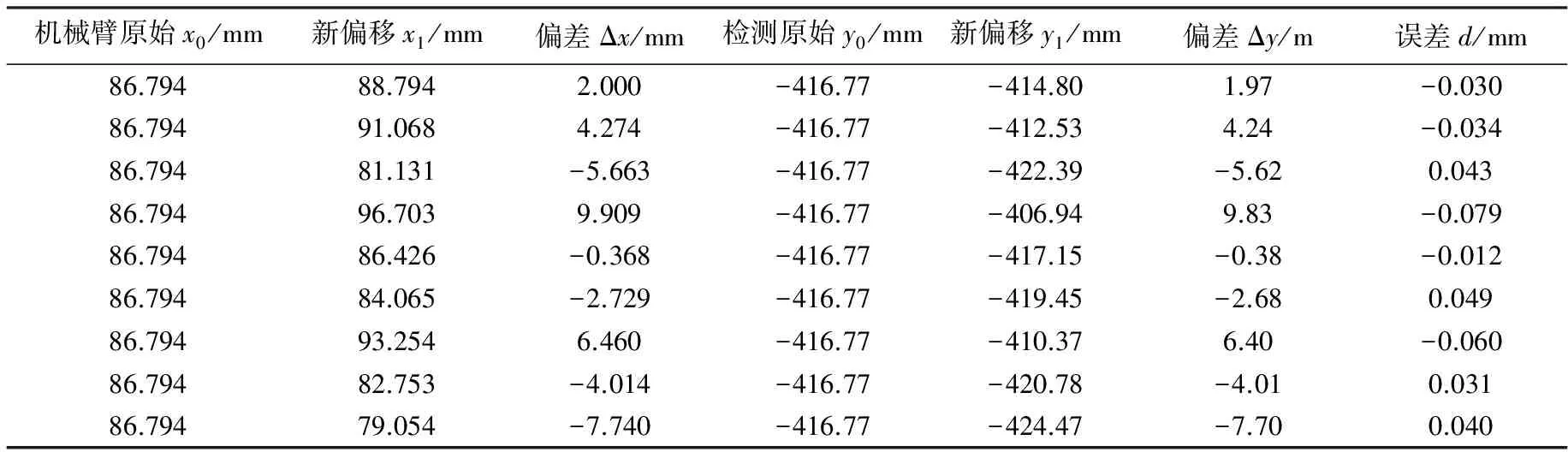
表 1 机械臂偏差值与算法偏差值对比误差

4 结 论

梯度投影直线检测方法能够很好地检测直线， 不需要事先对阈值进行选取， 就能直接进行直线检测， 具有很强的自适应能力， 并且可以避免传统方法中由于累加平面阈值参数选取不恰当所带来的直线检测误差. 对于玻璃银层有氧化、 孔洞及背景等干扰， 梯度投影法能够很准确地检测到待检测的直线. 该方法对复杂的情况具有一定的抗干扰能力. 梯度投影法能够快速准确地检测到直线且具有较高的检测精度， 能够满足玻璃焊带实时检测切割的要求.

[1] Gioi R G V, Jakubowicz J, Morel J M, et al. LSD: A line segment detector[J]. Image Processing on Line, 2012, 2(4)： 35-55.

[2] 倪金辉, 肖军, 文立伟. 一种基于直线拟合的预浸料边缘直线在线视觉检测方法[J]. 计算机科学, 2015, 42(s1)： 16-23.

Ni Jinhui, Xiao Jun, Wen Liwei. A linear fitting based on pre dip edge line detection method of online visual [J]. computer science, 2015, 42(S1)： 16-23. (in Chinese)

[3] 夏建春, 陈贤. 基于机器视觉的模切片缺失检测与定位研究[J]. 模具工业, 2012, 38(12)： 24-26.

Xia Jianchun, Chen Xian. Research on machine vision based die slicing defect detection and localization [J]. Die & Mould Industry 2012, 38 (12)： 24-26. (in Chinese)

[4] 朱良. 机器视觉在工业机器人抓取技术中的应用[D]. 沈阳： 中国科学院研究生院(沈阳计算技术研究所), 2016.

[5] 单小军, 唐娉. 图像匹配中误匹配点检测技术综述[J]. 计算机应用研究, 2015(9)： 2561-2565.

Shan Xiaojun, Tang Ping. Image matching error matching point detection technology [J]. Application Research of Computers, 2015 (9)： 2561-2565. (in Chinese)

[6] 冯亦东, 孙跃. 基于SURF特征提取和FLANN搜索的图像匹配算法[J].图学学报, 2015, 36(4)： 650-654.

Feng Yidong, Sun Yue. Image matching algorithm based on SURF feature extraction and FLANN search [J]. Journal of graphics, 2015, 36 (4)： 650-654. (in Chinese)

[7] 唐琎, 李青. 一种快速的模板匹配算法[J]. 计算机应用, 2010, 30(6)： 1559-1561.

Tang Jin, Li Qing. A fast template matching algorithm for [J]. computer application, 2010, 30 (6)： 1559-1561. (in Chinese)

[8] Savvides M, Juefei-Xu F. Image matching using subspace-based discrete transform encoded local binary patterns, US9171226[P]. 2015.

[9] Lindeberg T. Image Matching Using Generalized Scale-Space Interest Points[J]. Journal of Mathematical Imaging and Vision, 2015, 52(1)： 3-36.

[10] Balntas V, Tang L, Mikolajczyk K. BOLD - Binary online learned descriptor for efficient image matching[C]. IEEE Conference on Computer Vision and Pattern Recognition. 2015

[11] 任玲辉, 刘凯, 张海燕,等. 灰度投影积分极值法的矩形检测[J]. 计算机工程, 2012, 38(8)： 159-160.

Ren Linghui, Liu Kai, Zhang Haiyan, et al. Rectangle detection of grey integral projection extremum method [J]. Computer Engineering, 2012, 38 (8)： 159-160. (in Chinese)

[12] 孙煜杰, 杨欢, 吴政隆, 等. 基于灰度投影的跑道线提取方法[J]. 兵工自动化, 2015(11)： 9-13.

Sun Yujie, Yang Huan, Wu Zhenglong, et al. Method of racetrack extraction based on gray projection [J]. Ordnance Industry Automation, 2015 (11)： 9-13.(in Chinese)

[13] Gao X F, Shi Z H. An Improved Image Matching Algorithm Based on Gray Value Projection[J]. Aeronautical Computing Technique, 2012.

[14] 张文增, 陈强, 都东,等. 直线检测的灰度投影积分方法[J]. 清华大学学报(自然科学版), 2005, 45(11)： 1446-1449.

Zhang Wenzeng, Chen Qiang, Du Dong, et al. Gray-scale projection integration method for straight line detection [J]. Journal of Tsinghua University (Science and Technology), 2005, 45 (11)： 1446-1449.(in Chinese)

[15] Henderson C, Izquierdo E. Reflection Invariance： an important consideration of image orientation[J]. Computer Science, 2015.

[16] Costa J P D, Weisbecker P, Farbos B, et al. Investigating carbon materials nanostructure using image orientation statistics[J]. Carbon, 2015, 84： 160-173.

ResearchontheStraightLineDetectionAlgorithmofGlassWeldingBelt

LIU Fan1， ZHANG Quan1， LIU Yi1， ZHAO Ming1， GUI Zhiguo1,2

(1. State Key Laboratory of Electronic Measurement Technology (North University), Taiyuan 030051, China；2. Instrument Science & Dynamic Measurement, Ministry of Education Key laboratory of (North University), Taiyuan 030051, China)

In order to realize automatic cutting of glass welding tape with high efficiency and precision in industry, a kind of Projection Gradient Method (PGM) was put forward. Firstly, template matching was used on the detected original image to get sub-images including the lines that to be detected. Then these sub-images are projected in the vertical direction in order to obtain the gray projection vector. The gradient of gray projection vector is calculated to construct the gradient projection vector. Rotating the sub image around its center, when the detected lines parallel to the direction of its projection, the peak of gradient projection vector would be the largest. According to the image rotation and translation transformation, equations of detected lines could finally be formed. The experimental results showed that the gradient projection method could meet the requirements of real-time detection and cutting of glass welding belt.

glass welding tape; template matching; sub image; image rotation; line detection

1671-7449(2017)06-0461-08

2017-03-21

国家自然科学基金资助项目(61671413)； 山西省自然科学基金资助项目(2015011046)； 电子测试技术重点实验室开放基金资助项目(ZDSYSJ2015006)； 中北大学科研基金资助项目(XJJ2016019)； 山西省青年基金资助项目(201601D021080)； 山西省回国留学人员科研资助项目(2016-085)

刘 凡(1992-)， 男， 硕士生， 主要从事图像处理的研究.

桂志国(1972-)， 男， 教授， 博士， 主要从事图像处理与重建、 无损检测的研究.

TP391

A

10.3969/j.issn.1671-7449.2017.06.001