具有垂直传播及感染期的乙肝传播模型
2018-01-05陶玉杰冯贺平
陶玉杰,冯贺平
(1.通化师范学院 数学学院,吉林 通化 134000;2.河北软件职业技术学院 智能工程系,河北 保定 071000)
具有垂直传播及感染期的乙肝传播模型
陶玉杰1,冯贺平2
(1.通化师范学院 数学学院,吉林 通化 134000;2.河北软件职业技术学院 智能工程系,河北 保定 071000)
研究具有垂直传播和感染期的乙肝病毒感染模型,考虑了发生率函数为非线性时模型的性质,以乙肝的平均感染期作为时滞,利用Routh-Hurwite判别法得到了系统的疾病消失的平衡点局部渐近稳定的条件,找到了基本再生数R0,通过构造Lyapunov函数,证明了地方病平衡点的全局渐近稳定性.
乙肝模型;时滞;全局渐近稳定;非线性发生率;垂直传播
由乙肝病毒引起的乙型肝炎在世界范围内流行,乙肝感染威胁人类的健康,儿童及青壮年特别容易受到病毒的侵袭[1].乙型肝炎在中国流行广泛,是一种危害很大的疾病[2].因此,研究乙肝的流行趋势、传播规律及有效控制它的传播是亟待解决的问题.
数学模型在传染病的传播方式及疾病的控制研究方面有着重要的应用[3-4].用数学模型描述乙肝的传播动态能够为乙肝的预防和控制提供一定的参考[5-7].周兰等[8]提出了适合中国国情的乙肝传播动态数学模型;庞建华等[9]通过模型分析了疫苗及其他的控制手段对控制乙肝传播的影响;王开发等[10]提出了在有限区域内带有扩散及时滞的乙肝病毒感染模型;马之恩等[11]研究了具有空间分布及饱和发生率的乙肝传播模型;邱志鹏等[12]研究表明,虽然乙肝接种的增加直接影响艾滋病毒传播的减少,但是乙肝接种比例增加可能间接导致 HIV 流行的异常加速.
1 模型介绍
乙肝不仅通过日常生活传播,更主要的是家族之间的垂直传播.中国的乙肝患者中30%~50%是母婴之间垂直传播的.感染乙肝病毒的父母生育的新生儿在一出生的时候就可能已经被感染,导致乙肝的传播即具有水平传播又有垂直传播的特性[13-14].
在本文中,考虑了具有垂直传播、非线性发生率βSpI及乙肝病毒感染期的乙肝传播模型(1).模型中考虑了对乙肝感染者的连续治疗策略,假设S(t)、I(t) 及R(t)分别表示t时刻的乙肝易感者、乙肝病毒感染者以及康复者的数量.具体模型如下:
S′(t)=bm(S+R)-βSpI-bS+q′δI,
I′(t)=βSpI-βe-δτSp(t-τ)I(t-τ)+qδI-δI-γI-αI,
(1)
R′(t)=γI+βe-δτSp(t-τ)I(t-τ)-bR+bR+bm′(S+R)+αI.
模型的参数意义如下:
1)t时刻人口总数N=S+I+R,假设易感者和康复者生育的新生儿为易感者,感染者生育的没有被感染的新生儿也为易感者.
2)常数b>0表示乙肝感染者及康复者的出生率及死亡率,δ表示感染者的出生率和死亡率.正常数γ为乙肝感染者的自然恢复率,q(q≤1)为乙肝感染者的垂直传播率,记q′=1-q,q′ 3)βSpI表示易感者与乙肝病毒携带者接触的发生率,其中β为乙肝患者与易感者接触的有效传染率.τ>0为乙肝病毒的平均感染期,βe-bτSp(t-τ)I(t-τ)表示经过感染期τ后康复的个体数量. S′(t)=bm(1-I)-βSpI-bS+q′δI, (2) I'(t)=βSpI-βe-δτSp(t-τ)I(t-τ)qδI-δI-γI-αI. 定义 (3) 定理1如果R0<1,对所有的τ≥0,系统(2)的无病平衡点E0(m,0) 局部渐近稳定;如果R0>1,无病平衡点E0(m,0) 不稳定. 证明 系统(2)的平衡点满足下面的方程: bm(1-I)-βSpI-bS+q′δI=0; (4) βSpI-βe-δτSpI+qδI-δI-γI-αI=0. 显然,系统的无病平衡点为E0(m,0).在平衡点E0(m,0) 处将系统线性化,令S(t)=X(t)+m,I(t)=Y(t),则 X′(t)=-bX(t)+(q′δ-βm-bm)Y(t), Y′(t)=(βmp+qδ-δ-γ-α)Y(t)-βe-δτmpT(t-τ). 可以得到上面特征方程的其中一个特征根为λ1=-b<0,而另外一个特征根λ2由下面方程λ-βmp+βmpe-(δ+λ)τ+δ+γ+α-qδ=0决定. 令f(λ)=λ-βmp-βmpe-(δ+λ)τ+δ+γ+α-qδ,如果R0>1,对于实数λ,可得 因此,f(λ) =0 有一个正实根.故如果R0>1,无病平衡点E0(m,0) 不稳定. 若R0<1,平衡点E0(m,0)局部稳定.否则,Reλ≥0 与Reλ=(δ+γ+α-qδ)(R0e-Reλτcos(lnλτ)-1)≤(δ+γ+α-qδ)(R0-1)矛盾.因此,当R0<1时无病平衡点E0局部渐近稳定. 定理2如果R0<1,对所有τ≥0,系统(2)的无病平衡点E0(m,0) 全局渐近稳定. 如果R0>1,系统(2)存在唯一的正平衡点E1(S*,I*),其中 得到下面结论: 定理3如果R0>1,条件(7)及(9)满足,则对于所有的τ≥0,系统(2)的地方病平衡点E1(S*,I*)全局渐近稳定. 证明 令S(t)=X(t)+S*,I(t)=Y(t)+I*,得到线性化系统 由线性化系统得特征方程 λ2+Aλ+B+(Cλ+D)e-λτ=0, (5) 其中 A=δ+γ+α-qδ-βS*p+βe-δτS*p+b, B=(b+βI*S*p-1)(δ+γ+α-qδ-βS*p)+βI*S*(p-1)(βS*p+bm-q′δ), C=βS*pe-δτ, D=(b+βI*S*p-1)βS*pρ-δτ-(βS*p+bm-q′δ)βe-δτI*S*(p-1). 当τ=0时,特征方程变为 λ2+(A+C)λ+(B+D)=0 (6) 由式(5)可以看到当且仅当 A+C>0,B+D>0, (7) 所有的特征根都是负的. 当τ≠0 时,如果λ=ωi是特征方程(5)的根,有 -ω2+De-ωτi+Aωi+B+Dωe-ωτi=0, 分离实部与虚部,得到 B-ω2+Cωsinωτ+Dcosωτ=0, Aω+Cωcosωτ-Dsinωτ=0. 将上面的2个方程平方相加,得到如下的多项式方程 ω4+(A2-C2-2B)ω2+B2-D2=0, (8) 得 易得 A2-C2-2B>0,B2-D2>0. (9) 因此,当R0>1时方程(8)没有正实根,相应的可以证明,当R0>1 时,系统(2)的地方病平衡点E1(S*,I*) 是局部渐进稳定的. 接下来,讨论系统(2)的地方病平衡点E1(S*,I*) 全局渐近稳定的充分条件,首先给出下面的引理. 引理1[15]对所有的ξ∈[-τ,0),系统(1)满足初始条件S(ξ)=S(0)>0,I(ξ)=I(0)>0及R(0)>0,则对于t>0,系统(1)的解S(t)、I(t)及R(t) 都是正的. 引理2[15]对所有的ξ∈[-τ,0),系统(1)满足初始条件S(ξ)=S(0)>0,I(ξ)=I(0)>0及R(0)>0,则S(t) ≤max{1,S(0)+I(0)+R(0)}=M. 定理4对所有的ξ∈[-τ,0),系统(1)满足初始条件S(ξ)=S(0)>0,I(ξ)=I(0)>0及R(0)>0,当R0>1时,疾病感染期τ满足 其中M=max{1,S(0)+I(0)+R(0)},地方病平衡点全局渐近稳定. 证明 令S(t)=X(x)+S*,I(t)=Y(t)+I*,R(t)=Z(t)+Z*,得到下面的线性化系统 接下来,为了证明平衡点E1(S*,I*,R*) 的全局稳定性,构造Lyapunov函数 ρ(X(t)+Y(t))[-bX(t)-(γ+bm+α)Y(t)-βpe-δτI*S*(p-1)X(t-τ)- βe-δτS*pY(t-τ)]+Y(t)[βpI*S*(p-1)X(t)+βS*pY(t)-βpe-δτI*S*(p-1)X(t-τ)- βe-δτS*pY(t-τ)+(qδ-δ-γ-α)Y(t)]+Z(t)[βpe-δτI*S*(p-1)X(t-τ)+ βe-δτS*pY(t-τ)+(γ+α-bm′)Y(t)-bZ(t)]= -bρX2(t)-bZ2(t)-[ρ(bm+γ+α)-(qδ-δ-γ-α)-βSp]Y2(t)+[βpI*S*(p-1)- ρb-ρ(bm+γ+α)]X(t)Y(t)+(γ+α-bm′)Z(t)Y(t)-ρβpe-δτI*S*(p-1)X(t)X(t-τ)- (βρe-δτS*p+βe-δτS*p)Y(t)Y(t-τ)-(βρe-δτS*pX(t)Y(t-τ)-(ρβpe-δτI*S*(p-1)+ βρe-δτI*S*(p-1))Y(t)X(t-τ)+βρe-δτI*S*(p-1)Z(t)X(t-τ)+βe-δτS*pZ(t)Y(t-τ). 对上面的乘积项利用Cauchy-Chwartz不等式,可得不等式 令V(t)=V1(t)+V2(t),得到Lyapunov函数,则 将不等式V1(t)带入,得 本文研究了具有垂直传播及感染期的乙肝传染病模型的动力学性质.模型中根据疾病传播的特征采用了非线性发生率,考虑了乙肝的垂直传播特性,并且引入了乙肝的平均感染期,因此模型符合问题实际,通过分析得到了疾病消失与否的基本再生数R0,利用Routh-Hurwite判别法研究了平衡点的局部稳定性,通过构造Lyapunov函数证明了平衡点的全局稳定性,为制定和评测乙肝的防治策略提供一定的理论依据和参考.参 考 文 献: [1 ] JIA J D.Hepatitis B in China: from guideline to practice[J].Virol Sin,2008,23:152-155.DOI:10.1007/s12250-008-2953-8. [2 ] LU F,ZHUANG H.Management of hepatitis B in China[J].Chinese Medical Journal,2009,122: 3-4.DOI:10.3760/cma.j.issn.0366-6999.2009.01.001. [3 ] ALEXANDER M E,MOGHADAS S M.Periodicity in an epidemic model with ageneralized non-linear incidence[J].Mathematical Biosciences,189(1): 75-96.DOI:10.1016/j.mbs.2004.01.003. [4 ] 张冉.具有类年龄结构的传染病模型的全局性态分析[D].哈尔滨:黑龙江大学,2015. ZHANG R.Global behavior analysis of epidemic model with age - like structure[D ].Haerbin:Heilongjiang University,2015. [5] THORNLEY S,BULLEN C,ROBERTS M.Hepatitis B in a high prevalence New Zealand population: A mathematical model applied to infection control policy[J].Journal of Theoretical Biology,2008,254(3): 599-603.DOI:10.1016/j.jtbi.2008.06.022. [6 ] MEDLEY G F,LINDOP N A,EDMUNDS W J.Hepatitis-B virus endemicity: heterogeneity,catastrophic dynamics and control[J].Nature Medicine,2001,7(5): 619-624.DOI:10.1038/87953. [7 ] 宋运娜.具有脉冲接种、垂直传染的SEIRS 乙肝数学模型[J].复旦学报(自然科学版),2015,54(3):308-312. SONG Y N.A mathematical model of SEIRS hepatitis B with pulsed and vertical infection[J].Journal of Fudan University (Natural Science Edition),2015,54(3):308-312. [8 ] ZOU L,ZHANG W,RUAN S.Modeling the transmission dynamics and control of hepatitis B virus in China[J].Journal of Theoretical Biology,2010,262(2): 330-338.DOI:10.1016/j.jtbi.2009.09.035. [9 ] PANG J,CUI J,ZHOU X.Dynamical behavior of a hepatitis B virus transmission model with vaccination[J].Journal of Theoretical Biology,2010,265(4):572-578.DOI:10.1016/j.jtbi.2010.05.038. [10 ] WANG K,WANG W,SONG S.Dynamics of an HBV model with diffusion and delay[J].Journal of Theoretical Biology,2008,253(1): 36-44.DOI:10.1016/j.jtbi.2007.11.007. [11 ] XU R,MA Z.An HBV model with diffusion and time delay[J].Journal of Theoretical Biology,2009,257(3): 499-509.DOI:10.1016/j.jtbi.2009.01.001. [12 ] DING P,QIU Z,LI X.The population-level impact of HBV and its vaccination on HIV transmission dynamics[J].Mathematical Methods in the Applied Sciences,2016,39(18):5539-5556.DOI:10.1002/mma.3941. [13 ] LIU S J,ZHU Q.HBV disabusing and answering doubt[M].Beijing: Chinese Medicine and Scientific Technology Publishing Company,2003. [14 ] New Zealand Ministry of Health.Immunisation Handbook 2006[M].[S.l.]Wellington Ministry of Health,2006. [15 ] PEI Y,LI S,LI C,et al.The effect of constant and pulse vaccination on an SIR epidemic model with infectious period[J].Applied Mathematical Modeling,35(8): 3866-3878.DOI:10.1016/j.apm.2011.02.012 Cite this publication. HepatitisBvirusinfectionmodelwithverticaltransmissionandinfectionperiod TAOYujie1,FENGHeping2 (1.Department of Mathematics,Tonghua Normal University,Tonghua 134000,China; 2.Intelligent Engineering Department,Hebei Software Institute,Baoding 071000,China) Hepatitis B virus infection model with vertical transmission and infection period were studied.By consider the epidemic models with nonlinear incidence rate,making infection period as time delay,and making use of Routh-Hurwite criterion to prove that condition of disease-free equilibrium is local asymptotic stability,we obtained a basic reproductive numberR0and proved the global asymptotic stability of endemic equilibrium by using the Lyapunov functional method. HBV epidemic model; time delay; global asymptotic stability; nonlinear incidence rate; vertical transmission 10.3969/j.issn.1000-1565.2017.06.002 2017-02-17 吉林省教育厅资助项目(吉教科合字[2015]441) 陶玉杰(1975—),女,吉林通化人,吉林通化师范学院副教授,主要从事微分方程及应用控制方面的研究. E-mail:369387310@qq.com O175 A 1000-1565(2017)06-0567-05 王兰英)2 主要结果
2.1 无病平衡点的稳定性

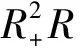


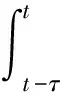
2.2 地方病平衡点的稳定性


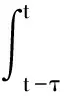



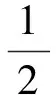



3 结论
