六自由度激励台的结构动力学等效建模

黄舟，黄海



六自由度激励台的结构动力学等效建模

黄舟1，黄海2

（1. 中国工程物理研究院 总体工程研究所，绵阳 621999；2. 北京航空航天大学 宇航学院，北京 100191）

六自由度激励台是多轴同步振动环境模拟的重要地面设备，因其结构复杂且具有多个运动自由度，而难以构建准确的结构动力学模型。文章针对6-PSU构型激励台的结构动力学特性，提出其参数型建模与模型修正方法。首先确定模型修正的对象为含轴承和导轨等接触运动副的铰链与作动部件，提出采用刚度与质量解耦的方法建立其含参等效动力学有限元模型；然后以该等效模型为基础，通过模态参数修正铰链和作动部件等效梁模型参数，再利用频响函数修正模型中轴承和导轨的接触刚度参数，得到了修正后的激励台等效结构动力学模型。修正后的有限元模型计算结果与试验结果吻合较好，验证了建模方法的有效性。

六自由度激励台；结构动力学；有限元法；模型修正

0 引言

六自由度激励台作为空间微振动环境模拟的重要设备[1]，与单轴激励台相比，由于可激励自由度的增加，其最大负载水平和工作频段均有所降低。随着受试产品质量的增大以及工作频率等要求的提高，六自由度激励台在使用中可能出现过试验、欠试验以及大量级共振等问题[2]。而对激励系统进行动力学建模与虚拟振动试验仿真[3-4]，则可以起到预试验的作用，从而提高振动试验的效率和成功率。

激励台的合理建模是虚拟振动试验的基础。文献[2, 5]在建模时将激励台简化为多体动力学模型，未考虑激励台中动圈和静圈等结构的柔性。文献[3, 6]中指出可通过模态综合的方法，把复杂结构动力学模型进行自由度缩聚，从而提高计算效率。文献[4]通过建立激励台三维有限元模型进行仿真分析，但六自由度激励台结构复杂，建立其详细有限元模型会使计算代价巨大。为在保证虚拟振动试验仿真精度的同时缩减自由度，可采用等效动力学建模[7]的方法对有限元模型进行简化，主要关注工作频段内激励台的低阶结构模态，进而将简化模型用于高效的振动模拟。因此，建立符合激励台结构特性的等效动力学模型，并基于振动试验对其进行合理修正[8]具有重要意义。

根据6-PSU（移动副-球副-虎克铰）构型六自由度激励台的结构特性，本文提出其等效动力学建模方法，并对该等效模型进行参数型修正与试验验证。首先采用解耦的方法对激励台中的铰链与作动部件建立含参等效动力学模型；然后利用模态参数修正铰链、作动杆中除轴承和导轨等接触运动副外的等效梁模型参数，进而利用频响函数修正轴承和导轨的接触刚度参数；以期得到与试验结果匹配的激励台结构动力学修正模型。

1 激励台结构特性

1.1 激励台结构布局

六自由度激励台结构如图1所示，主要包括台面、基座和6个作动杆。其中，台面用来安装负载和传感器等部件，与6个作动杆中的铰链相连；每个作动杆包含铰链和作动部件，通过控制器驱动作动部件中直线音圈电机进行伸缩运动，作动部件中的内筒组件在导轨的支撑下作轴向运动，通过铰链带动台面实现多轴振动。

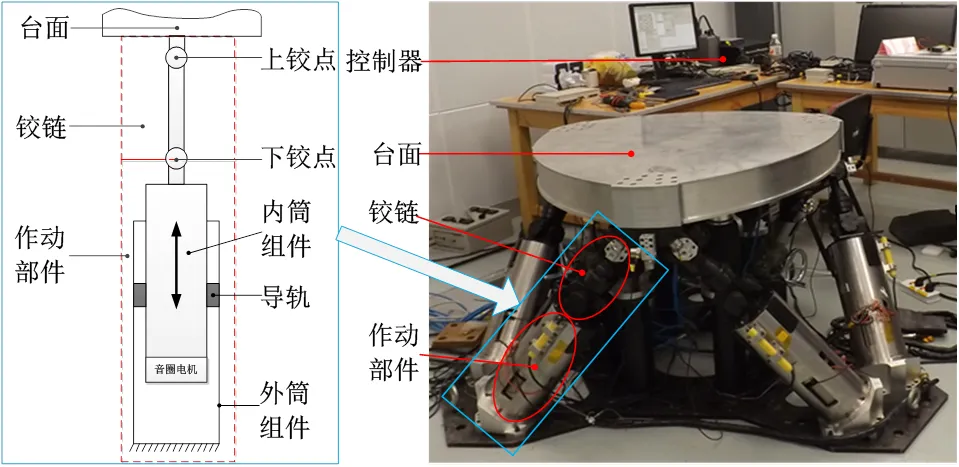
图1 基于6-PSU构型的六自由度激励台

1.2 频率响应特性

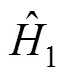
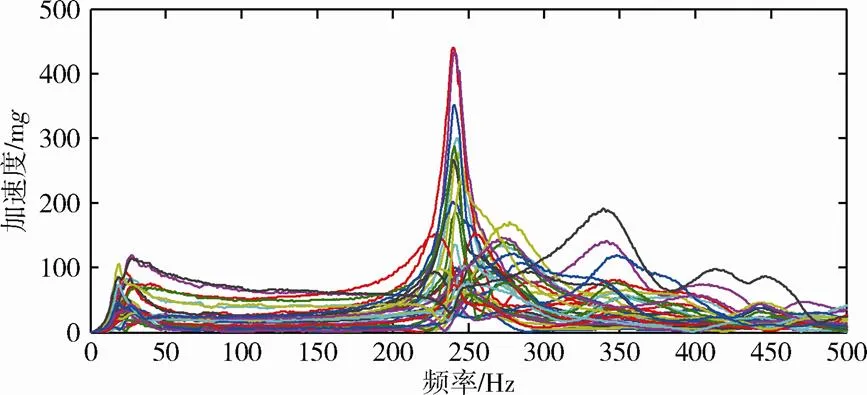
图2 激励台的幅频曲线

2 作动杆等效动力学建模

采用有限元方法进行结构动力学建模时，若对作动杆进行全尺寸、完整几何体建模，则模型修正的计算规模会非常庞大，不利于虚拟振动试验仿真。为降低作动杆模型的分析自由度，同时保留对动力学特性占主要贡献量的模态，可建立其等效动力学模型。等效动力学建模对象为作动杆（铰链和作动部件），包括轴承、导轨等具有相对运动自由度的部件，分别通过梁单元和弹簧单元来模拟作动杆结构和相对运动部件的接触刚度。

2.1 结构动力学等效建模方法

2.1.1 等效梁建模

在Nastran中CBAR欧拉梁单元的PBAR属性卡片如图3所示，卡片中包含了截面积，主惯性矩1、2和极惯性矩等4个梁截面参数。在MAT1材料卡片中包含了密度和弹性模量等2个输入参数。PBAR欧拉梁模型在修改截面参数时，质量和转动惯量会随着变化，而等效梁模型是在PBAR欧拉梁模型的基础上，将刚度和质量解耦分离，并与PBAR梁模型的刚度与质量等效。

图3 Nastran中的PBAR卡片

、1、2与分别为梁的轴向刚度、2个方向的弯曲刚度和扭转刚度，这4个刚度构成了等效梁单元的刚度矩阵。再将原CBAR梁单元的质量和转动惯量通过集中质量单元CONM2平均分配到梁单元的2个节点上，即可形成等效梁单元的集中质量矩阵。此时，将MAT1材料参数中的密度赋值为可视作0的小数值，从而不仅使等效梁模型与PBAR梁模型的质量等效，且在修正等效梁截面参数时不会改变质量矩阵，实现刚度与质量的等效与解耦。

该等效梁建模方法可通过一维梁模型的数值算例[10]来验证，对图4所示两端简支铝制梁建立等效梁模型进行模态分析，计算结果（将对称的弯曲模态视为同一阶模态）如表1所示。等效梁模型与欧拉梁解析解的前几阶固有频率的相对偏差很小，在数值上证明了等效梁模型的精度和有效性。

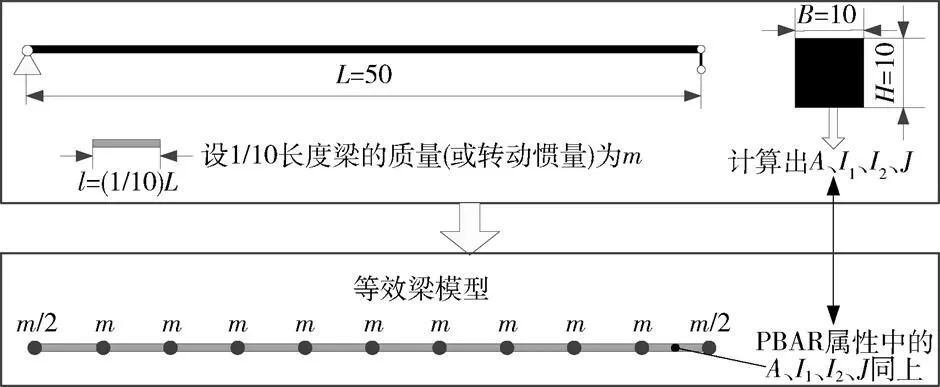
图4 简支梁的等效梁模型

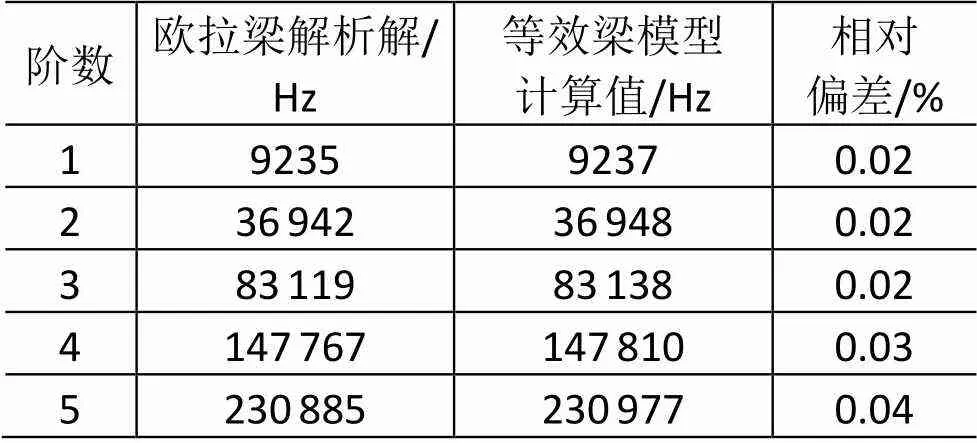
表1 梁模型的固有频率计算结果

2.1.2 接触刚度建模

Nastran中的六维广义弹簧单元CBUSH常用于模拟复杂装配结构结合面处的动力学特征[11]，其单元属性卡片PBUSH包含了如图5所示3个平动自由度和3个转动自由度的刚度值。在铰链点与导轨位置的相邻等效梁节点间建立CBUSH单元，再通过调节PBUSH中相应的刚度值，即可模拟铰链和导轨的接触刚度。

图5 Nastran中的PBUSH卡片

本文提出的等效建模方法与直接对三维模型缩聚自由度的方法[6]相比，等效梁模型包含了梁截面参数和接触部件刚度参数，参数的物理意义明确，便于后续分析和模型参数的修正，可更简单有效地组装形成激励台有限元模型。

2.2 铰链等效动力学模型

铰链的等效模型如图6所示，该模型分为下节叉梁、连接轴梁、连接座梁和上节叉梁4部分，采用等效梁模型进行建模。由于等效梁模型中梁单元每个节点有6个自由度，为模拟相邻梁之间在铰链点处的转动副，需要释放对应梁单元节点沿单元坐标系相应的转动自由度，如在连接轴梁下铰点处需释放R和R两个自由度。各段铰链梁截面的4个输入参数即是待修正的量。

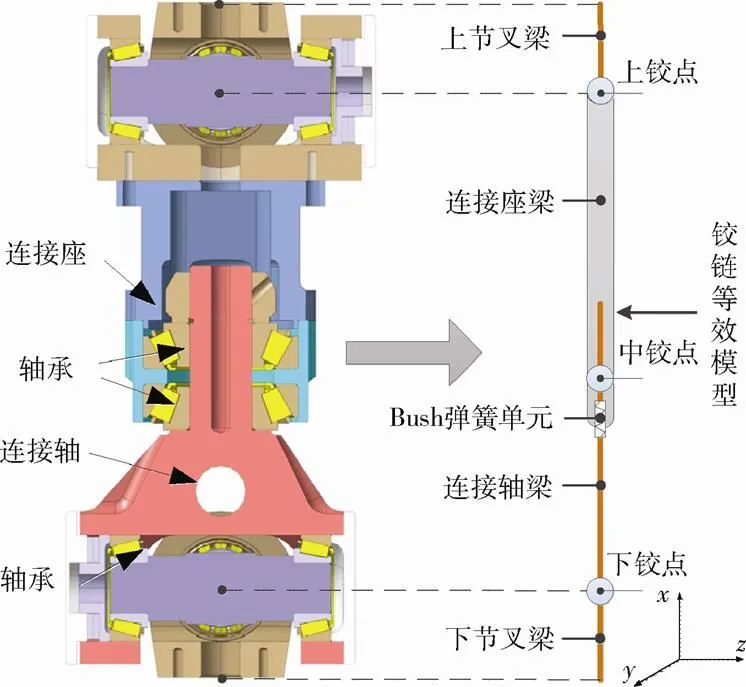
图6 铰链的等效模型示意

在铰链的上、下节叉和连接轴处共有3处轴承接触部位，但上、下铰点间的连接梁可认为是二力杆，铰链间的受力与相对变形为沿着铰链连线方向，因此可将3处轴承接触和螺栓连接等结合面的刚度折合到中铰点处。此时，在连接轴梁中铰点处的节点位置上串联一个CBUSH弹簧单元以模拟轴承的接触刚性。轴承接触传递的是U方向载荷，因此该CBUSH单元将除沿U方向外的刚度值设为一个大数，将U方向的接触刚度作为待修正值。

2.3 作动部件等效动力学模型

作动部件可分为内筒组件、外筒组件和导轨3部分，内筒和外筒组件均采用等效梁模型来建模，各部段模型如图7所示。内外筒之间的导轨通过CBUSH弹簧单元模拟，由于导轨可以沿着U方向运动，所以将U方向刚度值设为0。

3 等效动力学模型的参数修正

模型修正遵循“自下而上”的基本原则：先修正零件再修正装配体；先修正结构件再修正连接件。因此首先通过模态置信度准则MAC对铰链、作动部件进行修正，此时仅修正作动杆中的梁模型，将铰链中的弹簧模型设为绝对刚硬；再在全台模型修正中，通过频率响应函数置信度准则FRAC来修正弹簧模型的刚度值。

模态置信度准则MAC和频率响应函数置信度准则FRAC分别为[3]

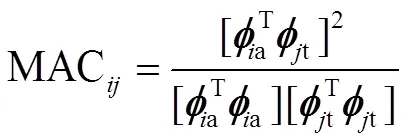
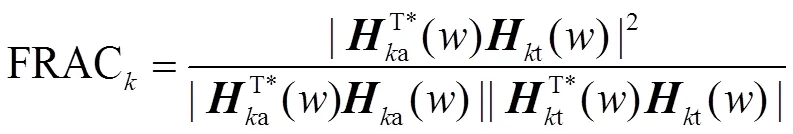
3.1 基于模态参数的作动杆模型修正

3.1.1 铰链模型的等效梁截面参数修正

在修正铰链模型中梁截面参数时，可采用全尺寸的三维有限元模型（见图8）来构建参考模型或试验模型，三维模型中轴承的接触刚度视为无限大，采用RJOINT刚性铰链单元建模。该三维有限元模型在进行模态分析后，提取出各阶固有频率以及与线框模型对应位置节点的振型，以得到与2.1节中等效模型节点自由度相匹配的参考模型。此时无须再进行模型缩聚或振型扩展[12]，2个模型的自由度数相同，边界条件均为下节叉底部固定。

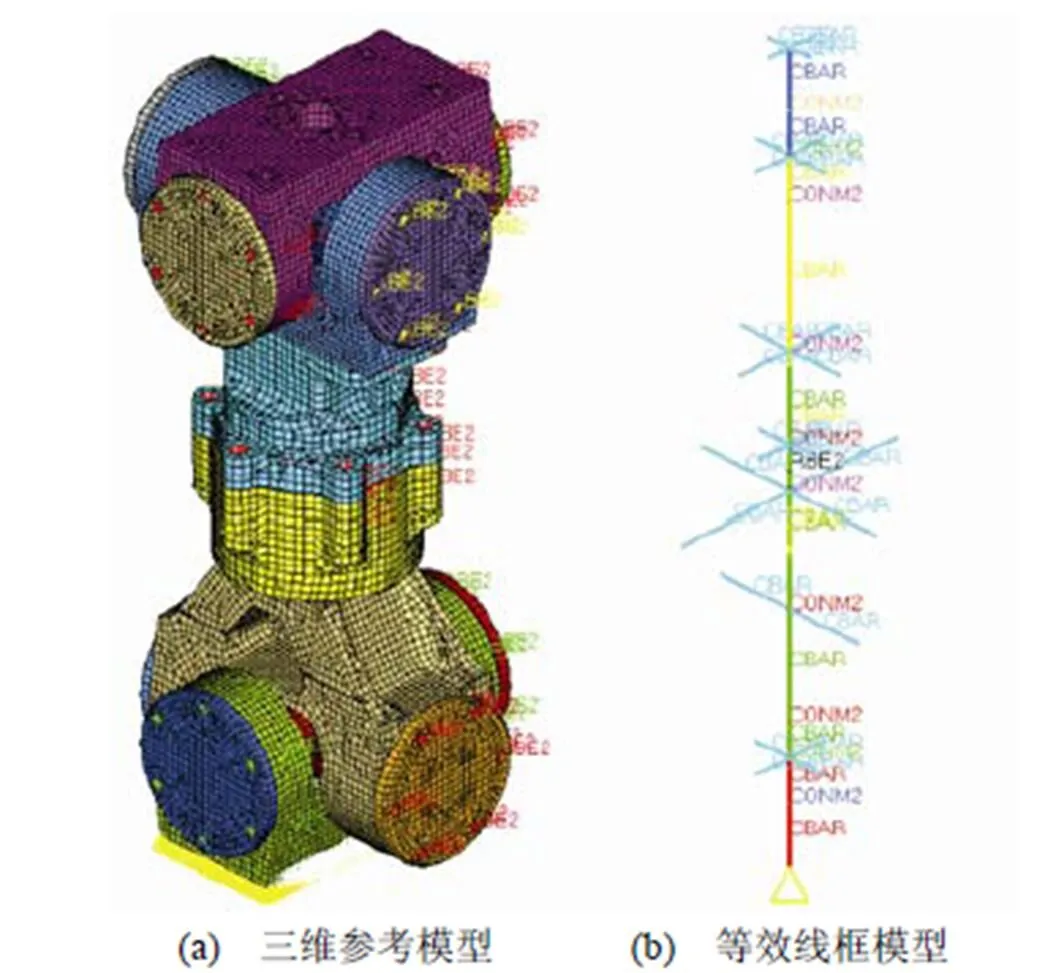
图8 铰链有限元模型

铰链参数型模型修正可转换为优化问题[13]，其数学表达式为

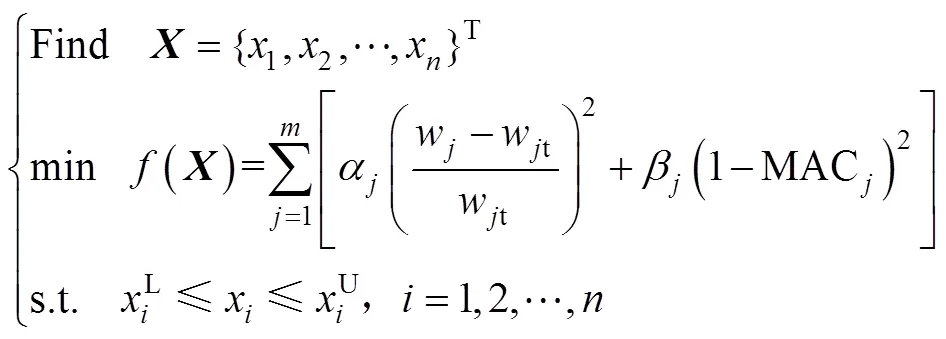
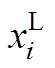
首先利用Nastran进行灵敏度分析，再通过Virtual Lab的SPQ序列二次规划法[14]进行优化计算，可得到各设计变量的优化解。由于各设计变量选取方法相同，本文仅以连接轴梁截面参数修正为例，修正结果见表2、表3和图9。

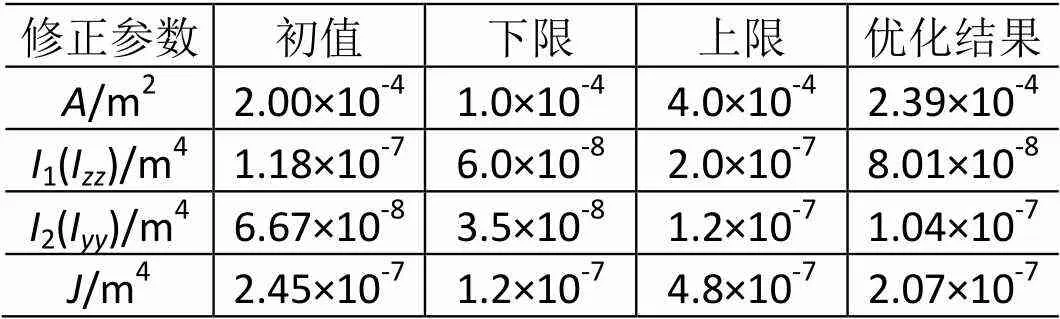
表2 连接轴梁修正前后的参数值

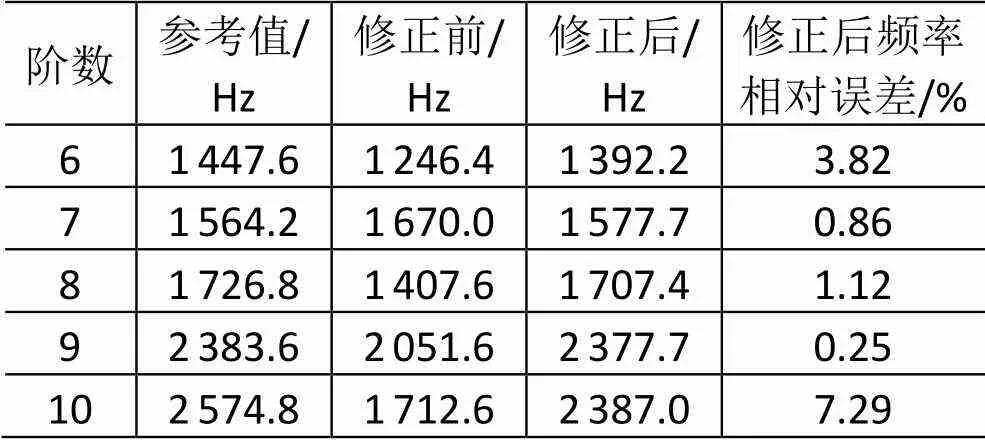
表3 铰链修正前后的固有频率

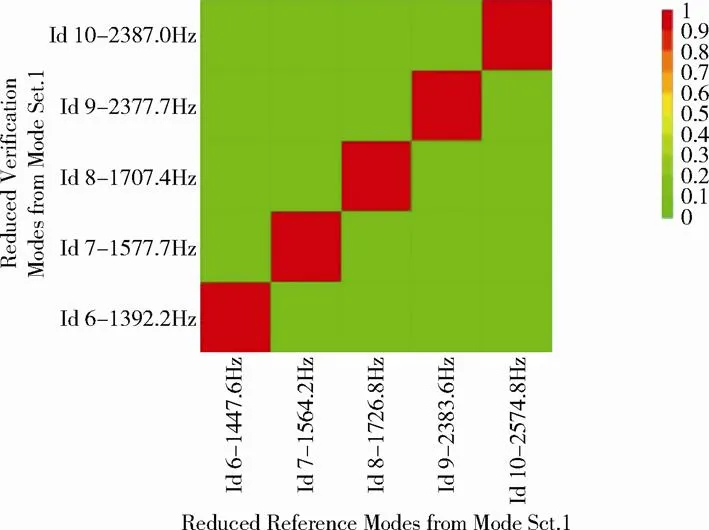
图9 铰链修正后的MAC值

修正后的铰链等效模型与参考模型相比，前5阶非刚体模态的频率相对误差较小，MAC矩阵数值接近单位阵，主对角线上的MAC值在0.95以上，表明频率和振型均符合得很好。这不仅验证了等效简化模型的合理性，且说明该模型可直接用于激励台有限元模型修正。

3.1.2 作动部件模型的等效梁截面参数修正

作动部件的修正方法和铰链类似，修正时仅考虑各个方向的1阶模态。图10为内筒组件的有限元模型，以内筒连接梁截面参数修正为例，修正结果见表4、表5和图11。由于内筒为局部开口结构，其一阶扭转模态振型相关性较差，对应的MAC值为0.745。考虑到内筒通过轴向伸缩传递电机力，与轴向模态相比，其扭转模态对激励台台面响应的影响较小，因此该修正结果工程上可以接受。

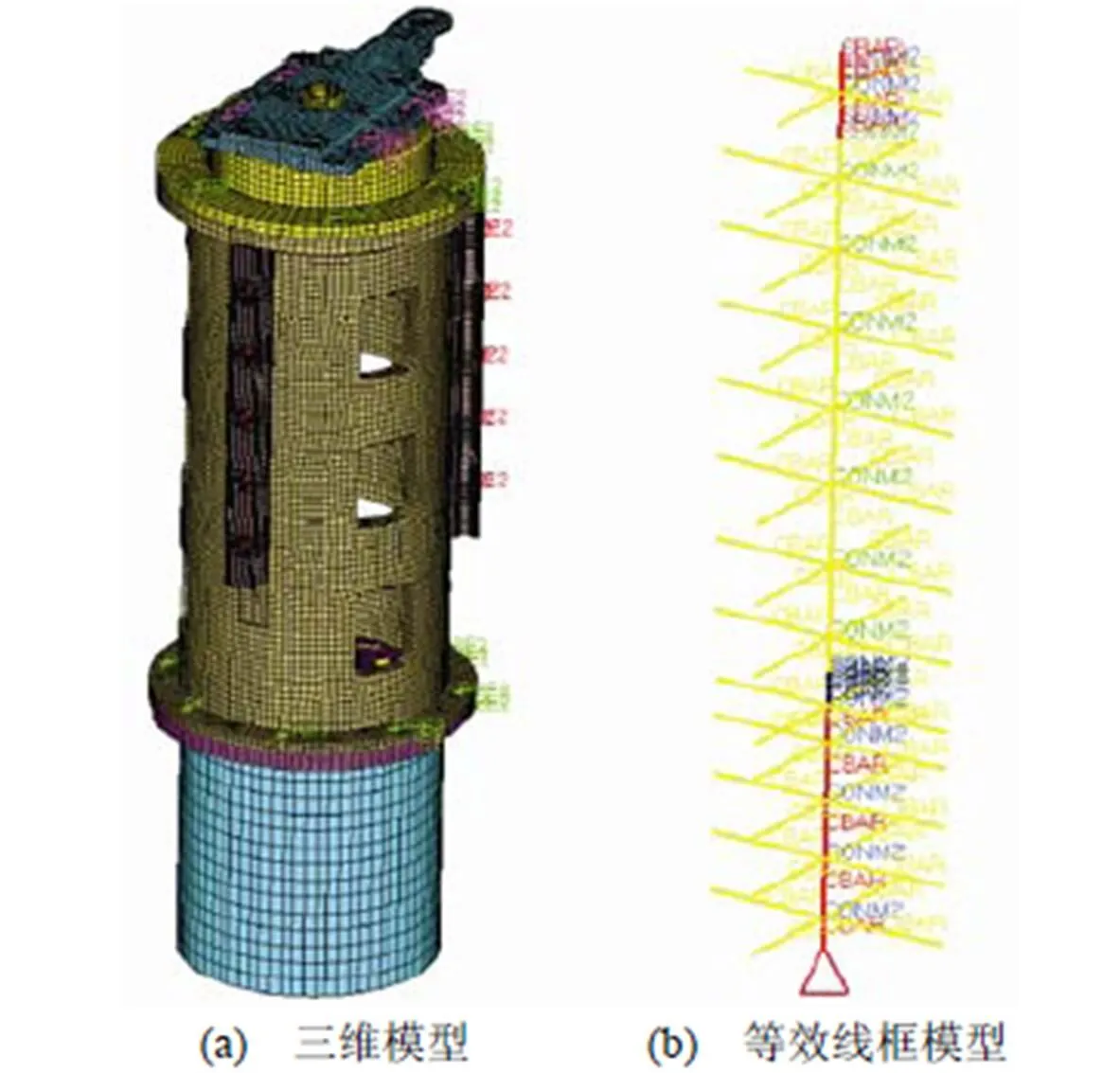
图10 内筒组件的有限元模型

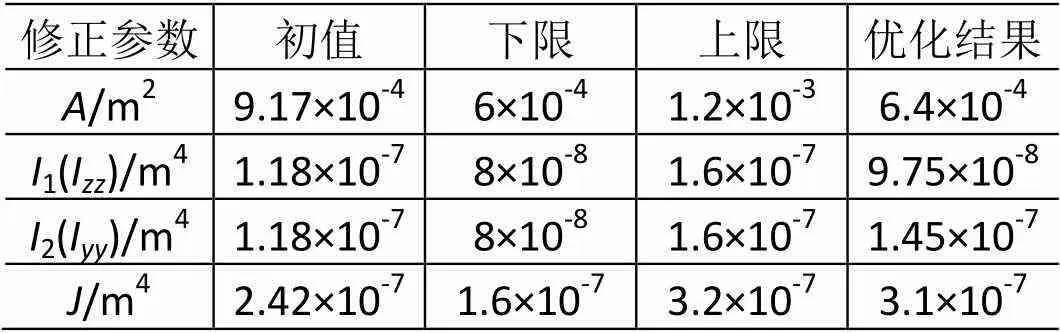
表4 内筒连接梁修正前后的参数值

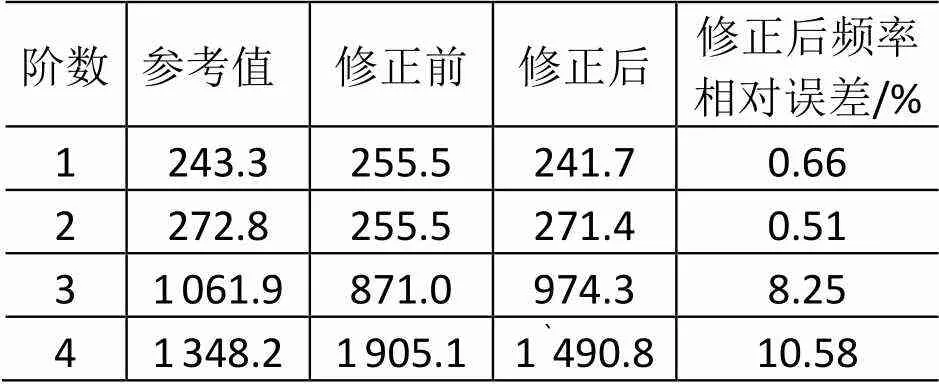
表5 内筒组件修正前后的固有频率

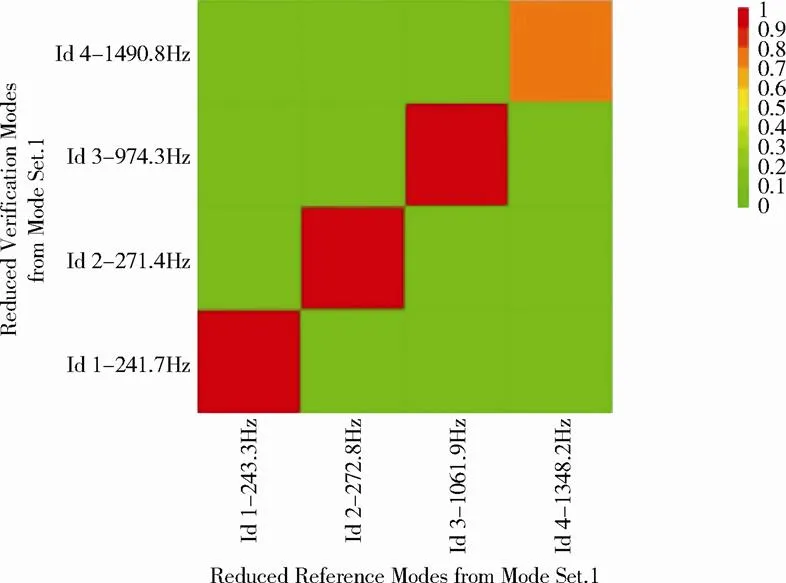
图11 作动部件修正后的MAC值

3.2 基于频响函数的激励台模型修正

作动杆中梁截面参数修正完成后，可通过计算仿真模型与试验模型中频率响应函数的相关性来进行激励台系统的模型修正。激励台参数型模型修正的数学表达式为

式中：设计变量={1,2,…,x}T为轴承和导轨的接触刚度，相关接触刚度的初始值可查阅文献[15]得到；()为目标函数，该加权函数通过各组输入输出点处的频率响应函数置信度准则FRAC与1的差值来构造，FRAC选取修正的频率范围为40～400Hz，加权系数α取为1；为了优化计算快速收敛，选择1号腿作为输入、1号和2号加速度计响应作为输出的频响进行修正，即取为2。

激励台有限元模型如图12所示，模型的边界条件为6个作动杆的外筒底部固定，采用模态叠加法计算以电机控制电压为输入、加速度计对应节点加速度为输出的频率响应。建模时激励力使用DAREA力载荷卡片，卡片中的比例因子（scale factor）设为电机的力电常数，激励沿着各作动杆的轴线方向，模型中的阻尼为3%阻尼比的模态阻尼。经过17步迭代计算后，1号和2号加速度计的频响曲线FRAC值分别达到0.791和0.783，修正结果见图13和表6，可以看到修正后模型的频响曲线与试验结果符合得较好，模型修正的结果理想，表明该模型具有较高的模拟精度。

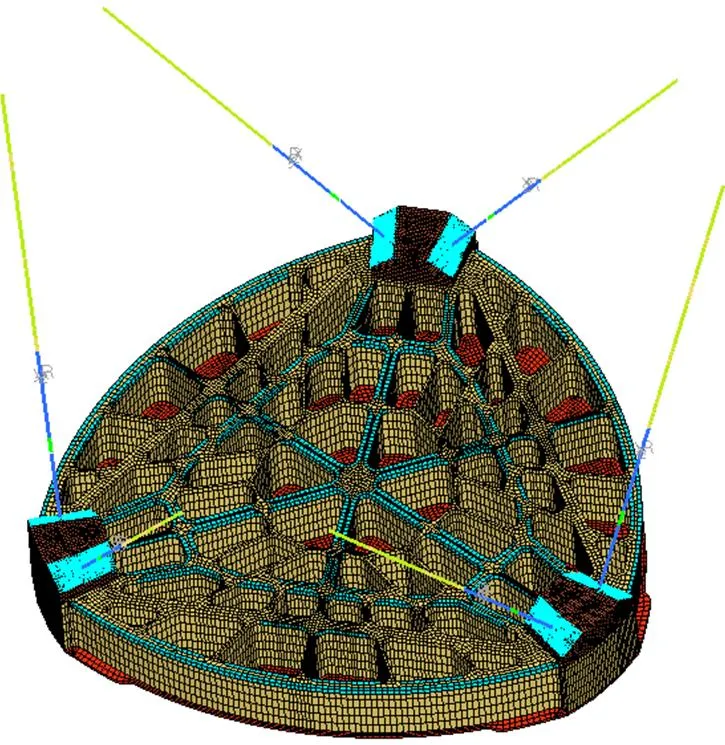
图12 激励台模型修正的全台有限元模型

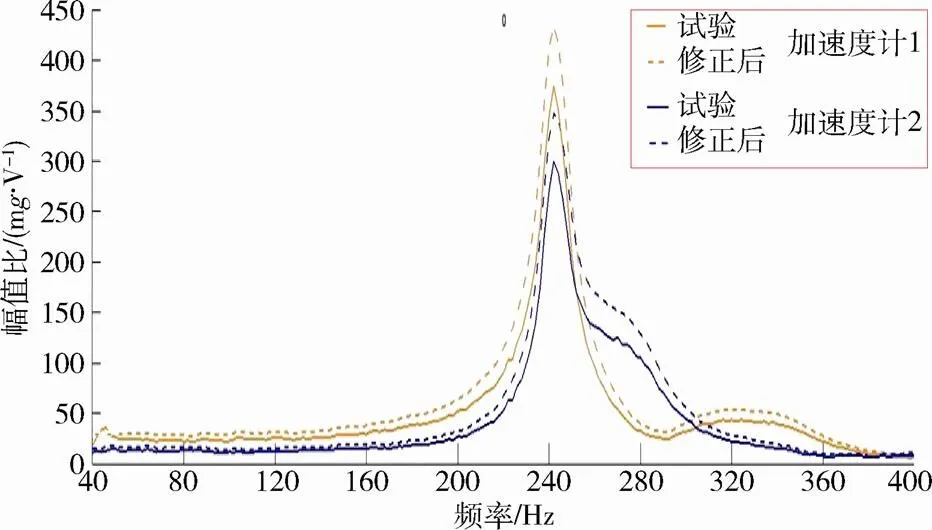
图13 修正后频率响应

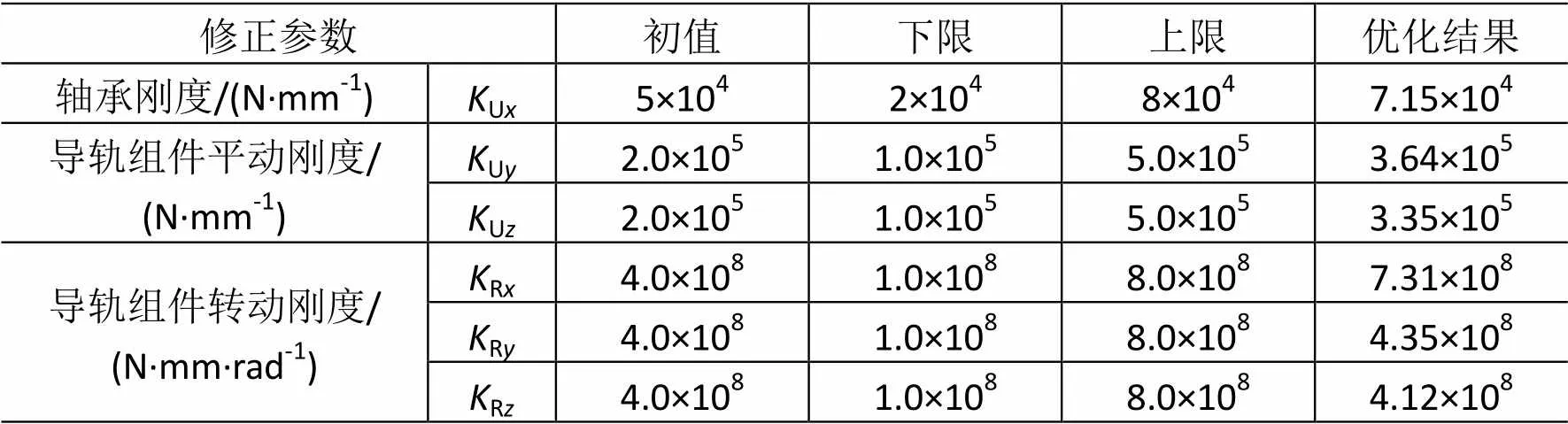
表6 模型中修正前后的接触刚度值

4 结论

本文给出了六自由度激励台有限元模型的等效动力学建模方法，在建立其解耦等效动力学模型后，分别通过模态参数和频率响应函数对等效模型中的参数进行了修正，得到与频率响应试验结果匹配的动力学模型，结论如下：

1）用等效梁模型建立作动部件、用CBUSH建立铰链，可以简化振动台建模，同时实现梁刚度和质量的解耦，且便于截面参数进行修正。该建模方法的对象也可推广到并联机构的支链中。

2）轴承和导轨接触刚度参数经有限次修正后，激励台仿真模型与试验结果频率响应吻合，表明修正后的模型可较好模拟激励台动力学特性，同时验证了修正方法的有效性。

[1] WANG H, HUANG H, ZHANG Z, et al. Multiple-degree-of-freedom sinusoidal vibration generation based on a hexapod platform[J]. Journal of Systems & Control Engineering, 2015, 229(2):139-148

[2]刘源, 董立珉, 孔宪仁,等. 飞行器虚拟振动试验平台构建[J]. 光学精密工程, 2013, 21(5):1258-1264

LIU Y, DONG L M, KONG X R, et al. Construction of virtual vibration testing platform for spacecraft[J]. Optics and Precision Engineering, 2013, 21(5):1258-1264

[3] 张正平, 邱吉宝, 王建民,等. 航天器结构虚拟动态试验技术新进展[J]. 振动工程学报, 2008, 21(3):209-222

ZHANG Z P, QIU J B, WANG J M, et al. Progresses on virtual dynamic test techniques for space vehicles[J]. Journal of Vibration Engineering, 2008, 21(3):209-222

[4] 刘闯, 向树红, 冯咬齐.卫星虚拟振动试验系统研究[J].航天器环境工程, 2009, 26(3): 248-253

LIU C, XIANG S H, FENG Y Q. Virtual vibration test system for satellite[J].Spacecraft Environment Engineering, 2009, 26(3): 248-253

[5] 谭永华, 蔡国飙. 振动台虚拟试验仿真技术研究[J]. 机械强度, 2010, 32(1):30-34

TAN Y H, CAI G B. Simulation on virtual testing of vibration shaker[J]. Journal of Mechanical Strength, 2010, 32(1):30-34

[6] 邱吉宝, 王建民. 航天器虚拟动态试验技术研究及展望[J]. 航天器环境工程, 2007, 24(1):1-14

QIU J B, WANG J M. A review on virtual dynamic test techniques for space vehicles[J]. Spacecraft Environment Engineering, 2007, 24(1):1-14

[7] 张旭, 吴志刚, 杨超. 基于等效梁模型的长直机翼动力学与颤振分析[J].北京航空航天大学学报, 2010, 36(11):1373-1377

ZHANG X, WU Z G, YANG C. Dynamic and flutter analysis of long-straight-wing based on equivalent beam model[J]. Journal of Beijing University of Aeronautics and Astronautics, 2010, 36(11):1373-1377

[8] 王明超, 杨光, 张卫国,等. 基于动力学模型修正的螺纹连接结构建模[J]. 振动与冲击, 2015, 34(23):161-165

WANG M C, YANG G, ZHANG W G, et al. Modeling for a bolt connected structure based on model updating[J]. Journal ofVibration and Shock, 2015, 34(23):161-165

[9] 李德葆, 陆秋海. 工程振动试验分析[M]. 北京: 清华大学出版社, 2004: 266-267

[10] 邢誉峰, 李敏. 计算固体力学原理与方法[M]. 北京: 北京航空航天大学出版社, 2011: 82-85

[11] 王春洁, 郭永. 着陆器软着陆机构的动力学分析[J]. 北京航空航天大学学报, 2009, 35(2):183-187

WANG C J, GUO Y. Dynamic analysis of lunar lander[J]. Journal of Beijing University of Aeronautics and Astronautics, 2009, 35(2):183-187

[12] 刘荣贺. 飞行器结构有限元模型修正算法及其应用软件研究[D].哈尔滨: 哈尔滨工业大学,2007: 10-11

[13] 鲍诺, 王春洁. 基于响应面优化的结构有限元模型修正[J]. 北京航空航天大学学报, 2014, 40(7):927-933

BAO N, WANG C J. Structural finite element model updating based on response surface optimization[J]. Journal of Beijing University of Aeronautics and Astronautics, 2014, 40(7):927-933

[14] 宋向荣, 李建康, 郑立辉,等. 基于模态相关分析的发动机曲轴箱模型修正[J]. 机械设计与制造, 2010(3):213-215

SONG X R, LI J K, ZHENG L H, et al.Finite element model modification of crankcase based on modal correlation analysis[J]. Machinery Design & Manufacture, 2010(3):213-215

[15] 方兵,张雷,赵继,等. 轴承结合部动态参数识别与等效分析模型的研究[J]. 西安交通大学学报,2012, 46(11):69-74

FANG B, ZHANG L, ZHAO J, et al. Dynamic parameter identification and modeling for bearing joint interfaces[J]. Journal of Xi’an Jiaotong University, 2012, 46(11):69-74

（编辑：许京媛）

Structural dynamics equivalent modeling for 6-DOF excitation platform

HUANG Zhou1, HUANG Hai2

(1. Institute of Systems Engineering, China Academy of Engineering Physics, Mianyang 621999, China; 2. School of Astronautics, Beihang University, Beijing 100191, China)

The six degrees of freedom(6-DOF) excitation platform is an important ground apparatus in the multi-axes vibration environment simulation. Because of its complex structure and multiple degrees of freedom of motion, it is difficult to build an accurate structural dynamic model. Based on the structural dynamic characteristics of the 6-PSU platform, a parametric modeling and model updating method is proposed. Firstly, the joints and the moving parts are regarded as the model modification objects, since they have their contact interfaces included in the bearings and the linear guides. And their equivalent dynamic models could be established with the proposed decoupling method for their stiffness and mass. Secondly, on the basis of the equivalent dynamic model, the beam cross section parameters for the structures of the joints and the moving parts are updated by using of the structural modal information. After that, the contact stiffness coefficients are revised using the frequency response function(FRF). Through the above steps, the updated finite element model for the 6-DOF platform is built. The comparison between the calculation based on the model and the FRF test show that the modeling approach is effective and valid.

6-DOF excitation platform; structural dynamics; finite element method; model updating

V416.2

A

1673-1379(2017)06-0611-07

10.3969/j.issn.1673-1379.2017.06.007

黄舟（1991—），男，硕士学位，研究方向为航天器振动试验设备的结构设计与优化；E-mail: huangzbuaa@163.com。黄海（1963—），男，博士学位，教授，研究方向为飞行器结构优化，空间智能结构及其控制等；E-mail: hhuang@buaa.edu.cn。

2017-08-13；

2017-11-24