单级行星齿轮非线性动力学模型与试验验证

刘 辉， 张 晨， 项昌乐， 王 成

(北京理工大学机械与车辆工程学院 北京，100081)

单级行星齿轮非线性动力学模型与试验验证

刘 辉， 张 晨， 项昌乐， 王 成

(北京理工大学机械与车辆工程学院 北京，100081)

针对单排行星直齿轮传动系统，提出了齿轮非线性啮合动态模型，模型中考虑了由中心距安装误差和传动轴弯曲变形等引起的中心距变化对啮合角、间隙和非线性啮合刚度的影响。考虑中心距变化和陀螺力矩并结合齿轮非线性啮合动态模型，建立了行星齿轮传动系统横-扭耦合非线性动力学模型。针对一个单排行星齿轮传统系统试验装置进行仿真计算和试验测试，试验对比分析了齿圈横向振动位移和内啮合均载系数。研究结果表明，仿真结果与试验结果的变化趋势基本吻合，且误差在可接受范围内，验证了笔者提出的渐开线直齿轮传动横-扭耦合非线性动力学模型和非线性动态啮合模型的正确性。

行星齿轮；啮合角；间隙；啮合力；动力学模型

引 言

齿轮传动系统单位质量、体积所传递的载荷增加，齿轮传动系统内部构件的变形也随之增加，严重影响齿轮传动系统的耐久性和可靠性。建立精确的行星齿轮动力学模型，预测齿轮传动系统的动力学行为，可为提高齿轮传动系统寿命和可靠性提供重要的理论依据[1-2]。

提高行星齿轮动力学模型精度需从非线性动力学角度建立模型，同时考虑轴和轴承的变形[3-4]。多数齿轮传动系统的啮合模型中，间隙取为定值，啮合刚度采用准静态的方法获得呈现周期时变特性，国内外学者基于该齿轮啮合模型做了广泛而深入的研究。文献[5-6]考虑定常间隙和周期时变刚度，建立了单级齿轮传动3自由度弯扭耦合非线性动力学模型，其中，啮合刚度采用准静态的方法获得。文献[7-8]考虑定常间隙和周期矩形波形式的时变刚度，分别针对两级齿轮传动系统和齿轮-转子耦合系统建立了多自由度非线性动力学模型。一些学者研究了齿轮运动状态对时变刚度、间隙和啮合角等啮合参数的影响。Chen等[9]考虑齿面、齿背啮合之间相位差，采用非对称矩形波形式的啮合刚度和定常间隙，基于6自由度弯扭耦合模型研究了齿轮空载敲击特性。Kim等[10]考虑齿轮横向位移对啮合角和重合度的影响，忽略间隙并采用矩形波形式啮合刚度，基于6自由度弯扭耦合模型研究了系统参数对齿轮动态特性的影响。Chen等[11]考虑齿轮中心距变化对间隙的影响，基于6自由度弯扭耦合模型研究了动态间隙对系统稳定性的影响，其中啮合刚度采用准静态方法得到。综上所述，文献[9-11]仅研究了齿轮运动状态对部分啮合参数的影响，未考虑齿轮中心距变化对啮合刚度的影响及各啮合参数之间的耦合关系对齿轮传动系统动态特性的影响。

笔者以单排行星齿轮为研究对象。首先，分别针对太阳轮-行星轮外啮合副和齿圈-行星轮内啮合副，考虑齿轮运动状态对啮合角、间隙和啮合刚度的影响及各因素之间的耦合关系对齿轮传动系统动态特性的影响，分析了中心距变化对啮合角和间隙的影响，以及齿轮传动过程转速波动和中心距变化对啮合点的影响，从而影响齿轮啮合力；其次，考虑中心距变化、陀螺力矩并结合齿轮啮合动态模型，采用拉格朗日法建立了横-扭耦合非线性动力学模型。

1 行星齿轮传动系统啮合模型

行星齿轮三维动力学模型如图 1所示。各齿轮和行星架均包含两个横向平移自由度xk，yk和一个扭转自由度θzk。其中：k=s，r，c，pi，分别代表太阳轮、行星架、齿圈和第i个行星轮，i=1,2…,N；N为行星轮个数。

图1 渐开线直齿行星齿轮传动三维动力学模型Fig.1 3D dynamic model of planetary transmission

1.1 太阳轮-行星轮动态啮合角

太阳轮与第i个行星轮的动力学模型在Oxy平面上的投影如图2所示。其中：虚线为初始时刻位置；实线为任意时刻位置；Cs和Cpi分别为太阳轮和行星轮的质心位置；es和epi分别为太阳轮和行星轮的偏心距；Oc为行星架的质心位置;αspi为啮合角;γspi为相对位置角。

图2 太阳轮和第i个行星轮二维投影模型Fig.2 2D dynamic model of sun and planetary gear pair

由几何关系得到太阳轮和第i个行星轮任意时刻的中心距，即动态中心距为

(1)

其中：RCpi和Rs分别为行星轮和太阳轮质心位置矢量。

Δx和Δy分别为

Δx=xc+rccos(φpi)+xpi+

epicos(φpi)-xs-escos(φs)

(2)

Δy=yc+rcsin(φpi)+ypi+

episin(φpi)-ys-essin(φs)

(3)

其中：rc为行星轮轴心Opi与行星架质心Oc之间的距离；φpi为第i个行星轮轴中心的位置角，φpi=θzc+φpi0，φpi0为第i个行星轮轴心的初始位置角；es和epi分别为太阳轮和行星轮的偏心距；φs和φpi分别为太阳轮和行星轮的自转角度，φs=θzs+φs0，φpi=θzpi+φpi0，φs0和φpi0分别为太阳轮和行星轮质心的初始位置角。

太阳轮与行星轮之间的动态啮合角为

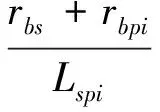
(4)

由几何关系可得太阳轮与第i个行星轮之间任意时刻的相对位置角为

(5)

其中：sign为符号函数。

Aspi和yspi分别如下

(6)

(7)

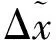
(8)

啮合力方向通过啮合线与坐标轴Oy的夹角ψspi判断。齿面啮合时，ψspi=αspi-γspi；齿背啮合时，ψspi=αspi+γspi。

1.2 齿圈-行星轮动态啮合角

齿圈和第i个行星轮的动力学模型在Oxy平面上的投影模型如图 3所示。其中：Cr为齿圈的质心位置；er为齿圈偏心距；αrpi为任意时刻啮合角；γrpi为任意时刻相对位置角。

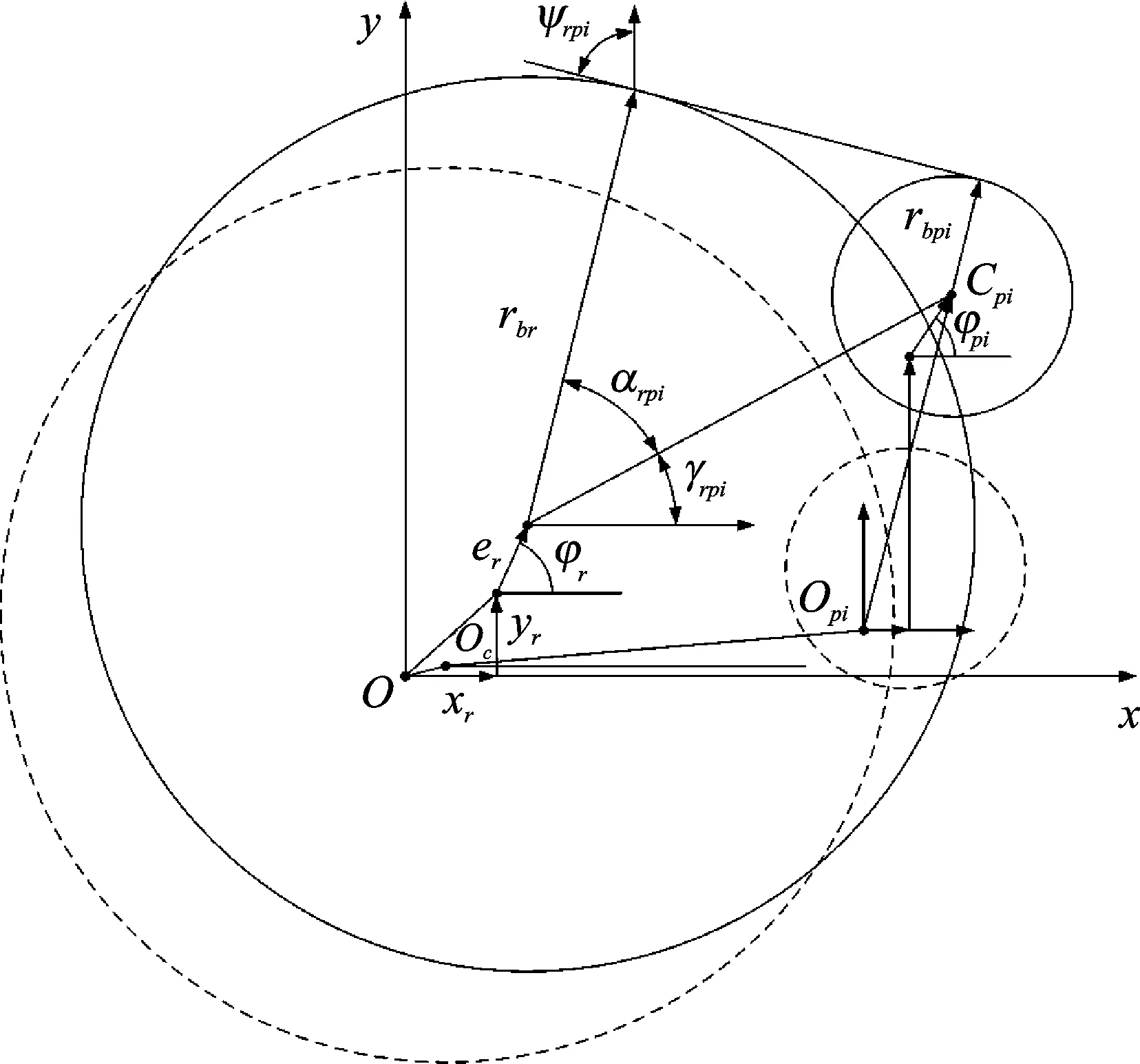
图3 齿圈和第i个行星轮二维动力学模型Fig.3 2D dynamic model of ring and planetary gear pair

由几何关系得到齿圈和第i个行星轮任意时刻中心距，即动态中心距为

(9)

其中：Rr为齿圈质心位置矢量。

Δx和Δy分别为

Δx=xc+rccos(φpi)+xpi+epicos(φpi)-

xr-ercos(φr)

(10)

Δy=yc+rcsin(φpi)+ypi+episin(φpi)-

yr-ersin(φr)

(11)

其中：φr为齿圈的转动角度，φr=θzr+φr0。

齿圈和第i个行星轮动态啮合角为

(12)

由几何关系可得任意时刻齿圈和第i个行星轮任意时刻的相对位置角为

(13)

其中：sign为符号函数。

Arpi和yrpi分别为

(14)

(15)

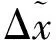
(16)

啮合力方向通过啮合线与坐标轴Oy的夹角ψrpi判断。齿面啮合时，ψrpi=αrpi+γrpi；齿背啮合时，ψrpi=αrpi-γrpi。

1.3 太阳轮-行星轮动态间隙

太阳轮-行星轮副间隙如图 4所示，其中：Lspi为动态中心距；αspi为动态啮合角。

动态齿侧间隙为

(17)

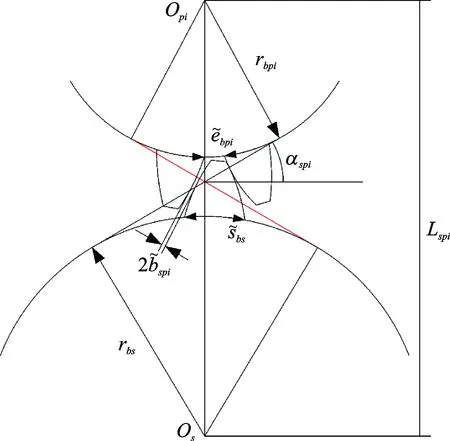
图4 外啮合齿轮副齿侧间隙Fig.4 Illustration of external meshing backlash

由图4中几何关系和渐开线性质，结合式(17)推导得到动态齿侧间隙为

(18)

1.4 齿圈-行星轮动态间隙

齿圈-行星轮组成的内啮合齿轮副的齿侧间隙如图 5所示，其中：Lrpi为动态中心距；αrpi为动态啮合角。由渐开线齿轮啮合原理可得动态齿侧间隙

(19)

由图5中几何关系和渐开线性质，结合式(19)推导得到动态齿侧间隙为

图5 内啮合齿轮副齿侧间隙Fig.5 Illustration of internal meshing backlash

(20)

1.5 太阳-行星动态非线性啮合力

太阳轮啮合点压力角与转速关系如图 6所示。坐标系Osxy在太阳轮的理论中心位置，坐标轴Oy始终指向行星轮的理论中心位置。旋转坐标系Osεη的中心在太阳轮的理论中心位置并随太阳轮旋转。由几何关系得太阳轮啮合点的压力角

(21)

其中：αspi0为啮合周期起始时刻啮合点压力角；t∈[t1,t2)，t1为啮合周期起始时刻，t2为啮合周期终止时刻；ωs为行星架的旋转坐标系下太阳轮的相对转速，定义逆时针为正，顺时针为负。

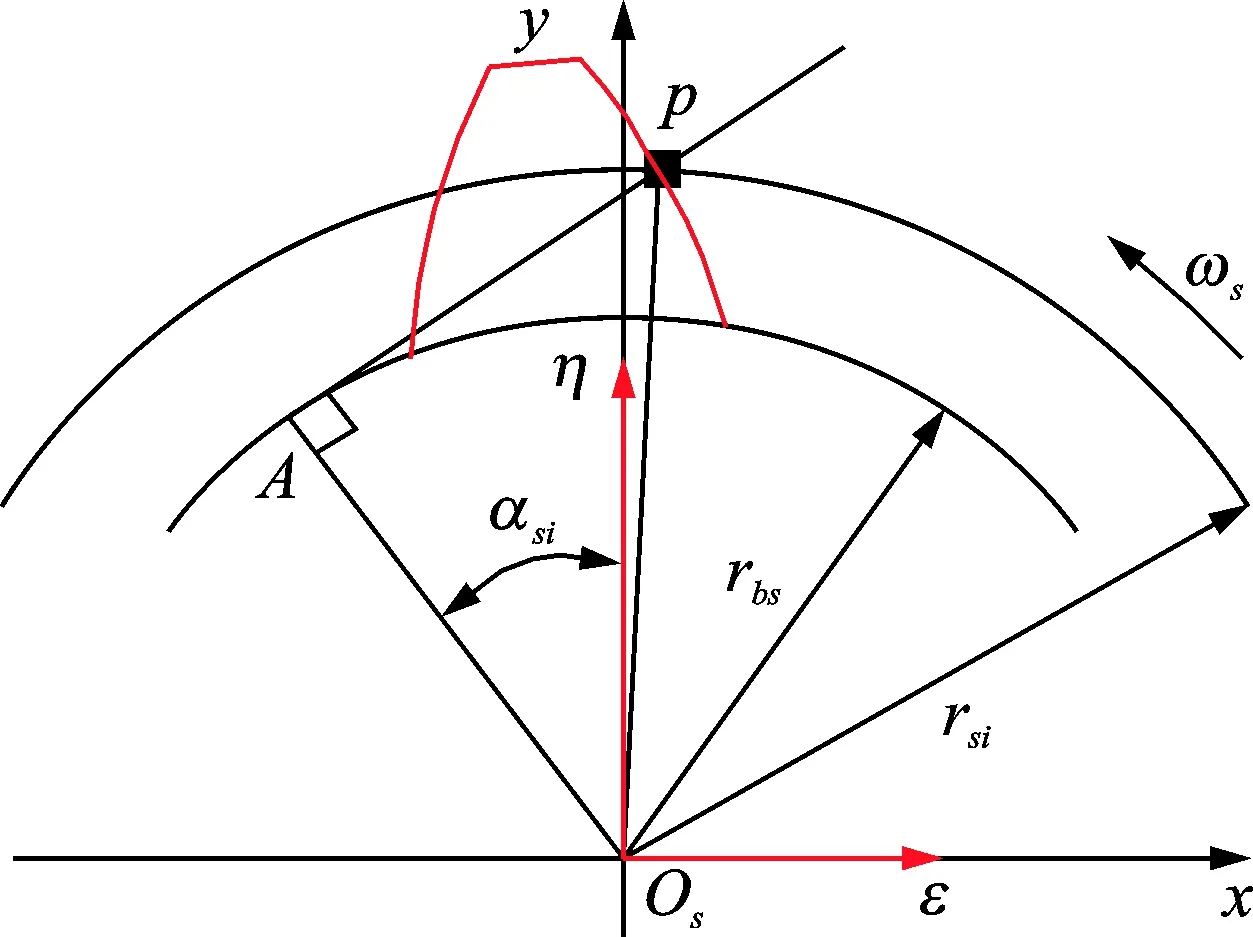
图6 啮合点速度分析Fig.6 Velocity analysis of meshing point

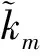
(22)

其中：αa，αb和αc为单、双齿啮合边界条件，由渐开线齿轮啮合原理得到；ks为单齿啮合区的啮合刚度；ks1，ks2分别为双齿啮合区不同齿对的啮合刚度。

本研究采用解析法计算单对齿啮合刚度。将动态齿侧间隙和动态啮合刚度代替以往啮合模型中定常间隙和准静态周期时变啮合刚度，可得太阳轮和行星轮之间动态啮合力为

(23)

f和f1的表达式分别为

(24)

(25)

动态传递误差分别为

Δspi1= (xs-xc-xpi)sin(αspi-γspi)+

(ys-yc-ypi)cos(αspi-γspi)+θzsRs-

θzcRs-θpiRzpi+Espi

(26)

Δspi2= (xs-xc-xpi)sin(αspi+γspi)-(ys-

yc-ypi)cos(αspi+γspi)-θzsRs+θzcRs+

θpiRzpi+Espi

(27)

其中：γspi为齿轮位置角；αspi为动态啮合角；Espi为由齿形误差等引起的齿形偏差。

1.6 齿圈-行星轮动态非线性啮合力

行星轮啮合点压力角与转速的关系如图 7所示。坐标系Opxy原点在行星轮的理论中心位置，坐标轴Oy反向始终指向齿圈的理论中心位置，旋转坐标系Opεη的中心为行星轮的理论中心位置并随行星轮旋转。由几何关系得任意时刻行星轮啮合点的压力角为

(28)

其中：arpi0为啮合周期起始时刻啮合点压力角；t∈[t1,t2)，t1为啮合周期起始时刻，t2为啮合周期终止时刻；ωpi为行星架的旋转坐标系下行星轮的自转速度，定义逆时针为正，顺时针为负。

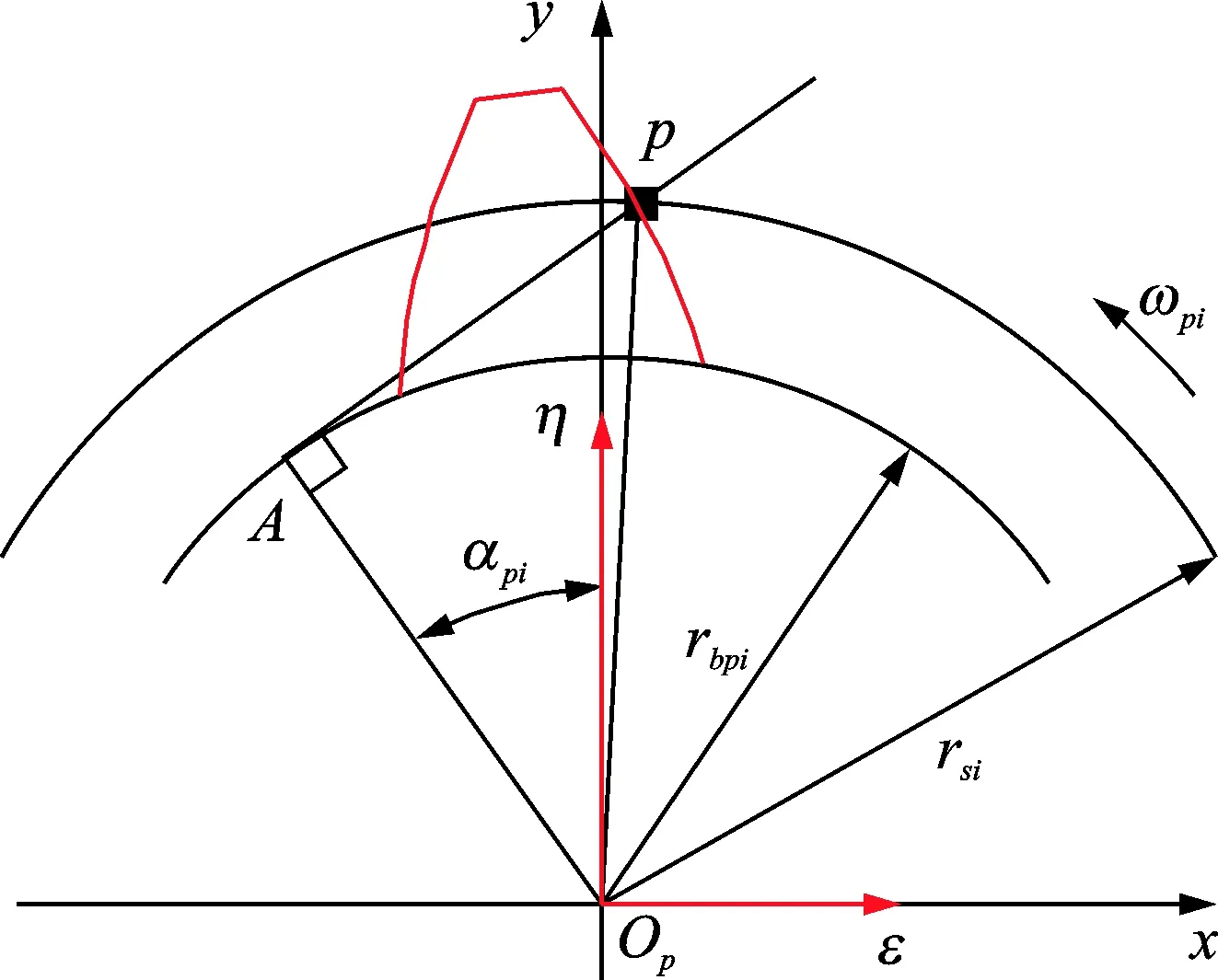
图7 啮合点速度分析Fig.7 Velocity analysis of meshing point

结合渐开线齿轮的啮合原理、动态中心距和动态啮合角可推导得出齿圈啮合点压力角

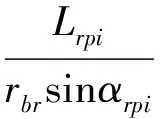
(29)

通过式(28)、式(29)可确定齿面或齿背啮合状态任意参与啮合轮齿的啮合点压力角。

对于齿圈和行星轮组成的内啮合副，采用解析法计算啮合刚度，单齿啮合刚度计算公式为

ks(αpi)=

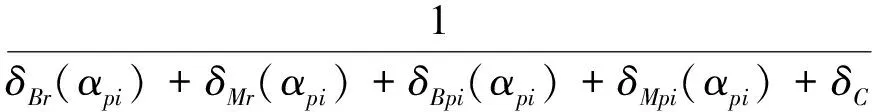
(30)

其中：δBr和δBpi分别为齿圈和第i个行星轮轮齿本身的变形；δMr和δMpi分别为齿圈和第i个行星轮轮体的附加变形；δC为轮齿之间的接触变形。

将动态齿侧间隙和动态啮合刚度代替以往啮合模型中定常间隙和准静态周期时变啮合刚度，可得齿圈和行星轮之间动态啮合力为

(31)

f和f1的表达式分别为

(32)

(33)

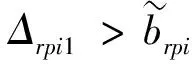
Δrpi1= (xr-xc-xpi)sin(αrpi+γrpi)-

(yr-yc-ypi)cos(αrpi+γrpi)+θzpiRpi-

θzrRr-θzcRr+Erpi

(34)

Δrpi2= (xr-xc-xpi)sin(αrpi-γrpi)+

(yr-yc-ypi)cos(αrpi-γrpi)-θzpiRpi+

θzrRr+θzcRr+Erpi

(35)

其中：γrpi为齿轮位置角；αrpi为动态啮合角；Erpi为齿形误差。

2 行星齿轮系统非线性动力学模型

通过拉格朗日方程建立系统动力学模型。动能函数包括太阳轮、齿圈、行星轮和行星架的动能函数，势能函数包含行星架与各行星轮之间的势能函数，而耗能函数等于0，未考虑传动轴和轴承等弹性元件。非保守力包括行星齿轮传动的内、外啮合齿轮副在齿面啮合、齿背啮合交替变化时产生的动态啮合力。结合图2和图 3，分别针对齿面、齿背啮合状态进行受力分析，将作用于太阳轮、齿圈和第i个行星轮各广义坐标上的非保守广义力组成列向量Qs，Qr和Qpi。将动能函数、势能函数和非保守力带入拉格朗日方程得出行星系统动力学方程。

太阳轮动力学方程为

(36)

齿圈动力学方程为

(37)

行星架动力学方程为

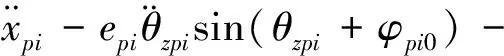
(38a)

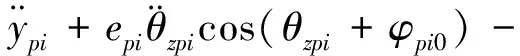
(38b)

(38c)

第i个行星轮动力学方程为

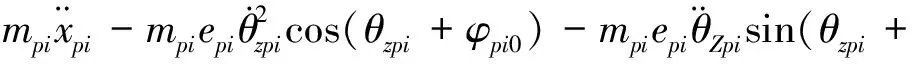
-Fspisin(αspi-Γspiγspi)+Frpisin(αrpi+Γrpiγrpi)

(39a)

-ΓspiFspicos(αspi-Γspiγspi)-

ΓrpiFrpicos(αrpi+Γrpiγrpi)

(39b)

φpi0))=rbpi(ΓspiFspi+ΓrpiFrpi)

(39c)

上式中Fxcpi和Fycpi如下

(40)

其中：Fspi和Frpi分别为太阳轮和齿圈与第i个行星轮之间的动态啮合力；齿面啮合状态时，Γspi=Γrpi=1；齿背啮合状态时，Γspi=Γrpi=-1；αspi和αrpi为动态啮合角；γspi和γrpi为相对位置角。

非线性动力学模型与非线性动态啮合模型反馈计算流程如图 8所示。

图8 计算流程Fig.8 Simulation flowchart

3 行星齿轮系统试验验证

针对单排行星齿轮传动试验装置分别进行数值仿真和试验测试，试验及模型中齿轮均未进行变位，且各齿轮参数如表1所示。

表1 单级行星齿轮传动参数表

行星齿轮传动试验台布置如图 9所示。

图9 单排行星齿轮传动试验台布置示意图Fig.9 Test diagram of planetary transmission

3.1 测试原理

3.1.1 齿圈齿根应变测试原理

在齿圈端面上选择8个轮齿作为测点，每两个相邻轮齿作为1组，各组工作片的相对位置相同且相距90°，温度补偿片的位置在靠近工作片的齿圈外侧，应变片的连接桥路采用单臂半桥方式连接。齿圈应变片粘贴图和连接桥路如图 10所示。

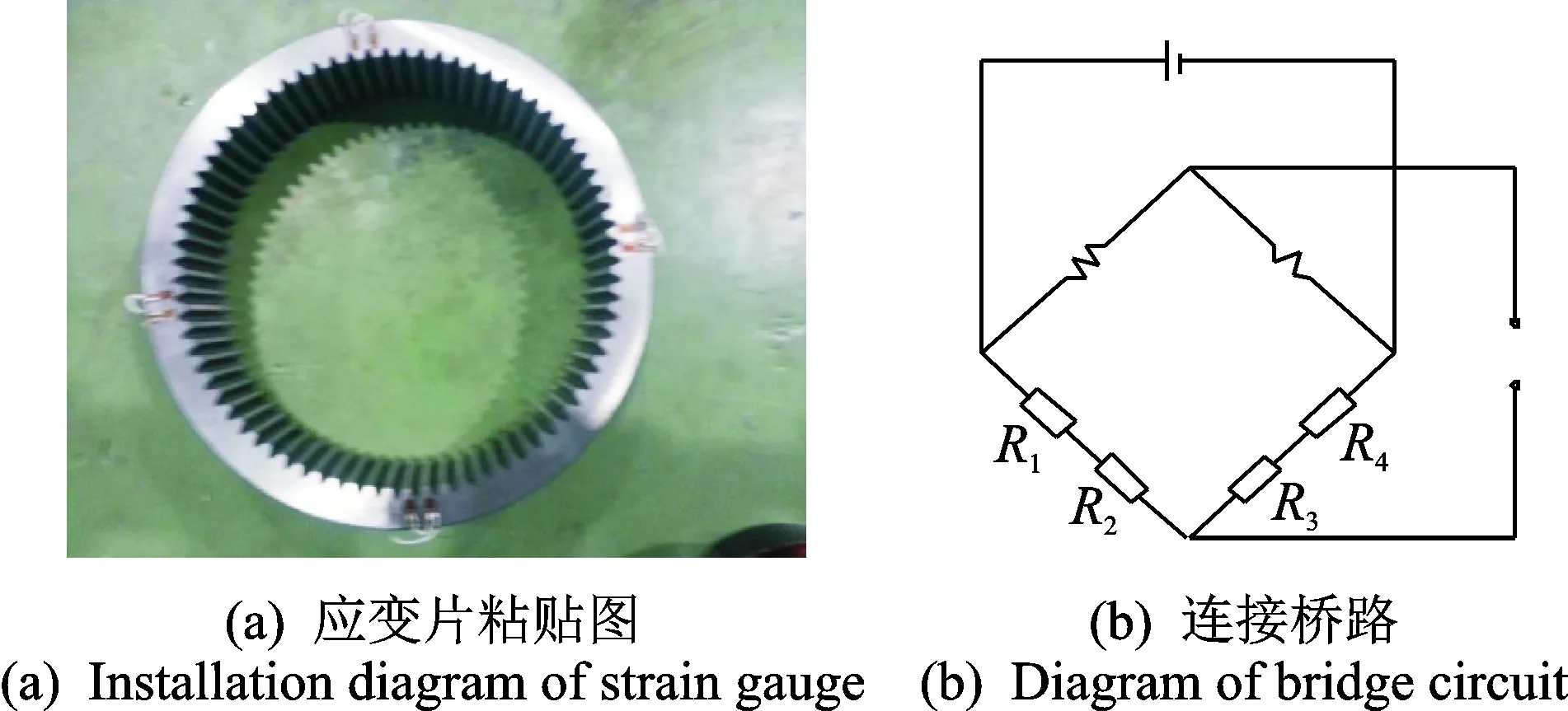
图10 齿圈应变片粘贴图和连接桥路Fig.10 Installation diagram of strain gauge and diagram of bridge circuit

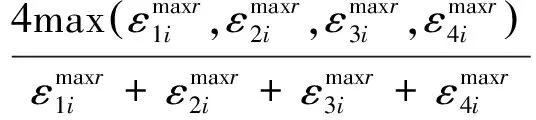
(41)

由采集时间内各短时信号内啮合均载系数，可得采集时间内的内啮合均载系数最大值为

(42)

其中：N为采集时间内所包含的短时信号的个数。

3.1.2 齿圈横向振动位移

在箱体的侧辅板上安装1个电涡流位移传感器，测试齿圈的横向振动位移，如图 11所示。位移传感器信号线通过箱盖上预留的导线孔伸出与控制器相联，从控制器出来的信号线再与数采前端连接。

图11 电涡流位移传感器安装图Fig.11 Installation diagram of eddy current displacement sensor

3.2 测试结果分析

静态条件下，电涡流位移传感器前端距齿圈表面0.8mm左右。输入转速为1kr/min，输入转矩分别为28和57N·m时，电涡流位移传感器试验结果如图12和图13所示。由图可知，传感器端面最远距离齿圈表面0.9mm左右，最近距离齿圈表面0.7mm左右，即齿圈的振动位移在0.2mm左右。结合频谱图，齿圈的横向振动位移的频率成分主要在0～200Hz范围内，包含输入和输出端转频及转频的倍频，同时存在一些无法分析原因的频率成分。

图12 齿圈振动位移(28N·m，1kr/min)Fig.12 Vibration displacement of ring(28N.m，1kr/min)

图13 齿圈振动位移(57N·m，1kr/min)Fig.13 Vibration displacement of ring(57N.m，1kr/min)

输入转速为3.5kr/min，输入转矩分别为28和57N·m时，位移传感器试验结果如图 14和图 15所示。由图可知，齿圈振动位移幅值在0.25mm左右，较转速1kr/min下的振动位移增加了0.05mm左右。结合频谱图，由于转速增加，齿圈的横向振动位移的频带变宽，频率成分主要集中在0～600Hz范围内，主要包含太阳轮和行星架的转频及转频的倍频，同样存在一些无法分析出原因的频率成分。

图14 齿圈振动位移(28N·m，3.5kr/min)Fig.14 Vibration displacement of ring(28N·m，3.5kr/min)

图15 齿圈振动位移(57N·m，3.5kr/min)Fig.15 Vibration displacement of ring(57N·m，3.5kr/min)

根据齿圈横向振动位移的试验结果，计算其峰峰值，将其与仿真计算结果进行对比。仿真结果与试验结果及两者之间的误差如表2所示。由表可知，随着转速和转矩的变化，仿真结果与试验结果均无明显变化趋势，且二者之间的最大相对误差为18.78%。

表 2 齿圈横向振动位移峰峰值

对于振动位移，仿真结果与试验结果之间产生误差的主要原因包括：a.电涡流位移传感器并非严格对准齿圈中心；b.仿真中齿圈简化为刚体，实际上在受力状态下齿圈会产生弹性变形；c.在测量过程中箱体辅板上的电涡流传感器会随着箱体的振动而振动。

由齿圈各测点的应变测试结果，结合式(41)和式(42)得到内啮合均载系数，将其与仿真计算结果进行对比。不同工况下内啮合均载系数的仿真结果与试验结果及误差如表3所示。由表可以看出，随着转速和转矩的变化，内啮合均载系数均无明显变化趋势。仿真结果与试验结果的最大相对误差为18.51%。

表3 内啮合均载系数对比分析

对于均载系数，造成仿真结果与试验结果之间产生误差的主要原因包括：a.由于采集系统通道数量，无法在每个齿根进行贴片，测试结果仅为几个离散位置的结果；b.不同应变片之间的粘贴方向无法完全相同；c.应变片的粘贴工艺、连接导线的阻抗和应变仪自身测量误差都对测试信号形成干扰。

4 结 论

1) 针对行星齿轮传动系统，分析了几何偏心、中心距偏差和横向位移引起的中心距变化对啮合角和间隙的影响，分析了齿轮的转速波动、齿轮中心距变化对啮合点位置的影响。分别针对太阳轮-行星轮与齿圈-行星轮提出了齿轮啮合动态模型，推导出齿轮中心距变化对啮合刚度、啮合力的影响。考虑中心距变化、陀螺力矩并结合齿轮啮合动态模型，采用拉格朗日法推导出行星齿轮横-扭耦合非线性动力学模型。

2) 针对单排行星齿轮传动试验装置，开展了振动特性试验研究。对比分析了多个稳态工况下齿轮传动系统中齿圈横向振动位移和内啮合均载系数的数值仿真结果与试验结果，并分析了可能导致仿真结果与试验结果之间产生误差的原因。结果表明，随着转速的增大，齿圈横向振动位移频带变宽，频率成分分布范围更广，且仿真结果与试验结果值均无明显波动，二者的变化趋势基本吻合，其误差在可接受范围内，从而验证了所提出的渐开线直齿轮传动横-扭耦合非线性动力学模型和非线性动态啮合模型的正确性。

[1] 李润方, 王建军. 齿轮系统动力学[M]. 北京: 科学出版社, 1996:132-133.

[2] Ozguven H N, Houser D R. Mathematical models used in gear dynamics-a review[J]. Journal of Sound and Vibration, 1988, 121:383-411.

[3] Wang Jianjun, Li Runfang, Peng Xianghe. Survey of nonlinear vibration of gear transmission systems[J]. Applied Mechanics Reviews, 2003, 56(3):222-227.

[4] Umezawa K, Houjoh H, Matsumura S, et al. Experimental investigation on modal behavior of a helical gear units with various ratio[C]∥Proceedings of the ASME Power Transmission and Gearing Conference. San Diego:[s.n.], 1996:509-517.

[5] Kahraman A, Singh R. Interactions between time varying mesh stiffness and backlash non-linearity in a geared system[J]. Journal of Sound and Vibration, 1991, 146: 135-156.

[6] 董海军, 沈允文, 高志英, 等. 转速激励下齿轮系统拍击振动的分岔特性[J]. 机械工程学报, 2006, 42 (2):169-172.

Dong Haijun, Shen Yunwen, Gao Zhiying, et al. Bifuration character of rattling in the gear system under the excitation of the rotational speed fluctuation [J]. Journal of Mechanical Engineering, 2006, 42 (2): 169-172.(in Chinese)

[7] Walha L, Fakhfakh T, Haddar M. Nonlinear dynamics of a two-stage gear system with mesh stiffness fluctuation, bearing exibility and backlash[J]. Mechanism and Machine Theory, 2009, 44:1058-1069.

[8] 崔亚辉, 刘占生, 叶建槐. 齿轮-转子耦合系统的动态响应及齿侧间隙对振幅跳跃特性的影响[J]，机械工程学报,2009,45(7):7-15.

Cui Yahui, Liu Zhansheng, Ye Jianhuai. Dynamic response of geared rotor system and the effect of clearance on jump characteristics of amplitude[J]. Journal of Mechanical Engineering, 2009,45(7):7-15.(in Chinese)

[9] Chen Z G, Shao Y M, Lim T C. Nonlinear dynamic simulation of gear response under the idling condition[J]. International Journal of Automotive Technology, 2012, 13:541-552.

[10] Kim W, HeeYoo H, Chung J. Dynamic analysis for a pair of spur gears with transla-tional motion due to bearing deformation[J]. Journal of Sound and Vibration, 2010, 329: 4409-4421.

[11] Chen Siyu, Tang Jinyuan, Luo Caiwang, et al. Nonlinear dynamic characteristics of geared rotor bearing systems with dynamic backlash and friction[J]. Mechanism and Machine Theory, 2011, 46:466-478.

10.16450/j.cnki.issn.1004-6801.2017.06.025

国家自然科学基金资助项目(51375047)

2015-12-11；

2016-05-03

TH113.1

刘辉，女，1975年10月生，教授、博士生导师。主要研究方向为车辆动力学。曾发表《A generalized dynamic model of geared system:establishment and application》(《International Journal of Computational Intelligence System》2011,Vol.4,No.6)等论文。

E-mail：lh@bit.edu.cn