双向驱动压电作动器结构设计
2018-01-04刘雪瑞黄卫清孙梦馨
刘雪瑞, 黄卫清, 王 寅, 孙梦馨
(1.南京航空航天大学机械结构力学及控制国家重点实验室 南京,210016)(2.华侨大学机电及自动化学院 厦门,361021)
双向驱动压电作动器结构设计
刘雪瑞1, 黄卫清1, 王 寅2, 孙梦馨1
(1.南京航空航天大学机械结构力学及控制国家重点实验室 南京,210016)(2.华侨大学机电及自动化学院 厦门,361021)
为了实现叠层压电作动器双向驱动、提高作动行程的目的,设计了利用三角位移放大原理的双向驱动压电作动器。分析了作动机构的运动及放大机理,建立了作动器的输出位移的理论模型和有限元静力模型。样机输出特性试验结果显示:压电作动器的位移放大倍数达5.45,与有限元仿真得到的放大倍数5.71以及解析计算得到的5.76倍相对偏差分别是4.77%和5.69%;驱动器在幅值为200 V正弦电压的激励下,作动行程达105.5 μm,作动行程与电压幅值具有很高的线性度(相关程度R2=0.997),且有很高的重复精度;作动器的输出特性受频率影响较小,频率每升高10 Hz,作动振幅减小0.04 μm;放大机构的迟滞效应相比单个叠层压电陶瓷有很大改善,迟滞回线中心对称。该结构实现了较大行程、双向对称驱动的目的,适用于需要往复驱动特性对称的应用场合。
叠层压电陶瓷; 微位移放大机构; 双向驱动; 迟滞效应
引 言
近年来,随着半导体制造、精密测量、生物工程及航空宇航等领域技术的发展和研究的深入,对运动控制系统提出了更高的要求,迫切需要高分辨率、大行程、快响应以及体积小巧的作动机构。作为精密机械与精密仪器的关键技术之一,压电微位移技术得到了迅速的发展[1]。压电微位移作动器尤其是叠层压电陶瓷作动器,作为一种新型微位移驱动元件,具有位移分辨率高、响应快、无噪声、刚度大及可微小化等优点,在微型机械制造、微机械装配、精密光学系统、纳米加工以及光纤对接等精密驱动领域得到广泛应用[2]。由于压电陶瓷的输出位移较小,即使是叠层压电陶瓷的输出位移一般也只有几微米到几十微米(通常只有其自身长度的0.1%)[3],而且随着输出位移的增加,叠层压电陶瓷的成本也大大增加,因此在实际应用中,常常需要将压电陶瓷驱动器的输出位移进行放大[3-10]。
目前,研究人员对微位移放大装置的研究主要集中在杠杆放大[4-5]、压曲放大[6-7]、桥式放大[8-9]及三角放大[10-11]等几种放大机构上。这些位移放大机构能够实现一定程度的位移放大,在精密驱动领域得到了广泛的应用。但这些常见的位移放大机构通常利用结构的弹性变形来放大叠层压电材料产生的变形,然而弹性放大限制了压电材料输出力大、响应速度快等优点的发挥,此外由于叠层压电陶瓷可以承受较大压应力而不能受到拉应力,因此难以实现往复运动机构的对称运动。
为克服上述问题,文献[1]提出了一种基于改进三角放大原理的菱形微位移放大机构,以柔性铰链作为传动结构,实现了双向主动驱动,放大倍数达到2.4倍。在此基础上,笔者设计了一种双向驱动压电作动器,旨在现有的加工、装配水平下,所生产的驱动器在驱动过程中能够尽量避免产生传力部件的弹性变形,实现一维双向作动。该位移放大机构以叠层压电陶瓷作为核心驱动单元,利用三角放大原理,将4个叠层压电陶瓷菱形对称布置,在实现输出位移放大的同时,获得双向对称的作动特性。通过理论计算以及有限元仿真,分析其静态和动态特性,并通过试验对其位移放大的效果、频率特性进行了研究。
1 作动器结构设计
为了实现位移放大和双向对称驱动,笔者提出的作动器结构如图1所示。
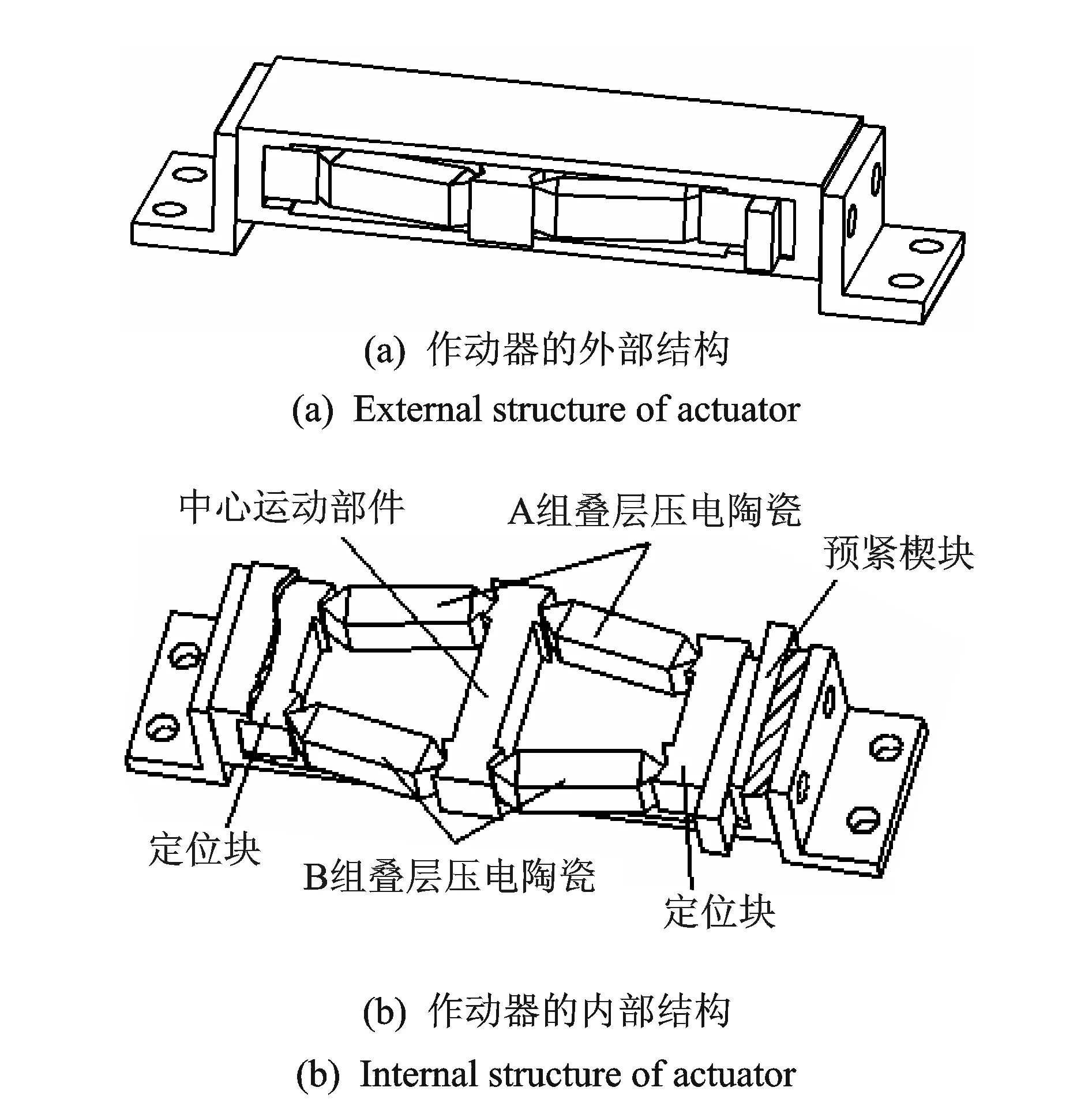
图1 作动器结构Fig.1 Structure of actuator
如图1(b)所示,驱动器包含4个菱形分布的叠层压电陶瓷,分为上下两组。为了保证将叠堆产生的位移直接传递到中心运动件上,同时减小三角块和定位块之间的摩擦,叠层压电陶瓷两端固定了三角块,三角块与定位块之间线线接触。位于中央的中心运动部件通过和它线线接触的4个三角块与四个叠层压电陶瓷相连接。内部驱动结构通过预紧楔块压紧固定,同时提供叠层压电陶瓷工作状态下必要的预紧力。
2 驱动器工作原理
2.1 三角放大原理
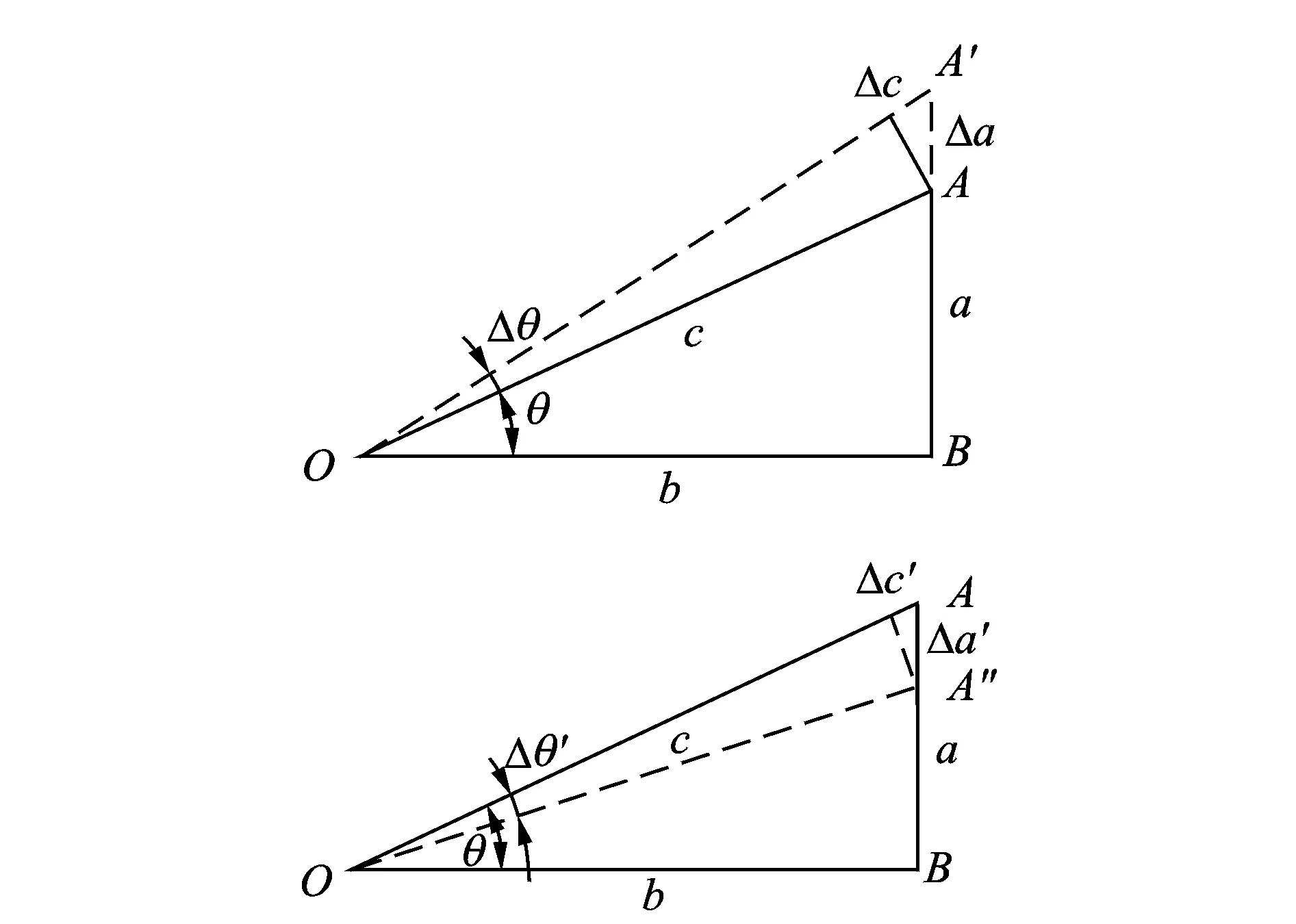
图2 三角放大原理Fig.2 Triangle amplification principle
三角放大原理如图2所示。设短直角边为a,长直角边为b,斜边为c,长直角边与斜边的初始角为θ。当长直角边b保持不变,斜边c伸长Δc时,短直角边a伸长Δa,根据勾股定理得
b2=c2-a2=(c+Δc)2-(a+Δa)2
(1)
Δc2+2cΔc=Δa2+2aΔa
(2)
忽略二阶小量,得放大机构的放大倍数
(3)
当叠层压电陶瓷缩短时,同样能得到式(3)。由式(3)可知,笔者所采用的三角位移放大倍数β只与叠层压电陶瓷和横坐标的夹角θ有关系,理论上可以通过减小夹角θ无限制增大机构的位移放大倍数。由于sinθ≥1 ,放大倍数β≥1。
2.2 作动器驱动原理
根据三角放大原理设计的菱形双向驱动压电作动器,如图3所示,其菱形的四边与两条对角线构成4个直角三角形,对斜边上的叠层压电陶瓷产生的位移进行放大,中心运动件为菱形的短对角线。

图3 驱动器激励信号Fig.3 Exciting signal of actuator
当一组叠层压电陶瓷同时伸长或者缩短相同的长度时,在中心运动件上产生的输出位移大小相同,方向相反。
设计驱动信号如下。
A组叠层压电陶瓷两端电压为
UA=U0+UC
(4)
B组叠层压电陶瓷两端电压为
UB=U0-UC
(5)
其中:U0为基础恒定电压,用于避免叠层压电两端电压为负值使其退极化(U0大于UC的峰值);UC为控制电压,通过调节UC对中心运两端的输出位移进行大小、方向等进行控制,当UC=0时,机构处于平衡位置。
由于叠层压电陶瓷伸长量在低频下近似与电压呈线性关系[12-13],设伸长量与施加电压的关系为
δ=nd33U-nF/k0
(6)
其中:n为叠层压电陶瓷的陶瓷片数;d33为压电应变系数;F为压电叠堆上所受外力;k0为单个陶瓷片的刚度。
假设中心运动部件为刚体,则有
βδA=-βδB
(7)
化简得
nd33U0=nF/k0
(8)
式(7)中,中心运动件的位移为
βδA=βnd33UC
(9)
由式(8)、式(9)可知,基础恒定电压U0不能使运动件运动,只转化为叠层压电陶瓷中的应力;当结构参数和叠层压电陶瓷一定时,运动部件的位移只与控制电压UC有关,且与控制电压的大小呈正比,通过控制电压控制运动部件运动的方向和大小。
2.3 预紧装置
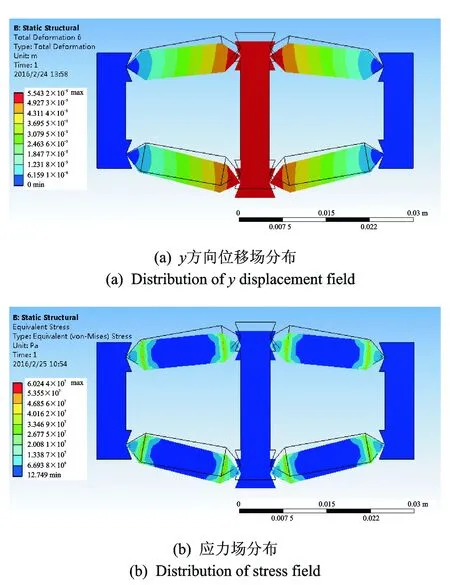
为了使叠层压电陶瓷工作在最佳状态,并在工作状态下能够稳定,需要设计预紧机构实现对叠层压电陶瓷预紧力的连续施加。如图4所示,选用楔块作为预紧和自锁装置。通过在楔块两端加力F1来对每个叠层压电陶瓷施加均等的预紧力,此时装置不能自锁。当施加预紧力后楔块只受预紧力合成的正压力F2, 需要楔块具有自锁的能力, 因此楔块的结构参数α 图4 预紧楔块Fig.4 Preload device 采用有限元法对提出的作动器进行静力学仿真分析。结构选用弹簧钢65 Mn,将其视为各向同性材料,屈服极限σs≥784 Mpa 。简化结构模型只保留作动部分,如图5所示,取结构参数θ=10°,结构的总体长为54.4 mm,宽为27 mm,理论放大倍数约为5.76。 图5 有限元仿真分析Fig.5 Finite element analysis 利用Ansys workbench软件对结构进行建模,叠层压电陶瓷部分材料采用PZT压电陶瓷材料(锆钛酸铅)进行近似替代。设置定位块两个外框为固定边界,三角块与叠层压电陶瓷绑定为一体,三角块与定位块以及中心运动件的V型凹槽为线线绑定接触。 当叠层压电陶瓷两端施加电压使输出位移为 9.7 μm 时,如图5(a)所示,放大机构在中心作动件作动方向y方向输出位移为55.4 μm,放大倍数约为5.71倍。放大倍数的理论解和有限元解非常接近,这说明结构的理论简化十分合理。 图5(b)为作动部分的应力场分布,可以看出,在三角块间断和三角块与叠层压电陶瓷连接的部分为应力集中的部分,距离该连接部分2 mm及以上,应力逐渐均匀并减小到稳定值。可以选用更加耐磨、耐疲劳的材料制作三角块。 根据上面的设计分析,设计制作了样机,并对该机构进行了性能测试。本研究中的叠层压电陶瓷采用丹麦NOLIAC公司 NAC2013-H14型的叠层压电陶瓷, 该陶瓷长14 mm,最大自由伸长位移为20 μm。样机驱动部分尺寸采用有限元建模的尺寸,如图6所示,整机外形尺寸为54.4 mm×27 mm×10 mm 。试验前将其分为两两一组,各自两端通过胶将三角块粘在叠层压电陶瓷两端,并分别对称安装于固定外壳中,构成菱形的放大机构。通过2个预紧楔块对4个叠层压电陶瓷施加预紧力,预紧力加载到50 N。 图6 装配图Fig.6 Assembly diagram 低频下中心运动件输出位移仅与控制信号有关,设置控制信号UC为正弦波,基础电压U0为正弦波的幅值(即由信号发生器产生两路完全偏置且相互反相的正弦信号)。在此激励下,中心运动件在平衡位置做简谐振动,保持信号频率为20 Hz,改变电压幅值,从10 V起,以10 V的幅度依次升压到200 V。系统测试如图7所示,样机被固定在隔振台上,通过激光位移传感器(基恩士LK-H1W,最小分辨率为1 nm)的激光垂直于中心运动件的位移输出表面,得到中心运动件的输出位移,由电脑读取测量数据。为了减少随机误差对结果的影响,每个电压对应的振幅均取5组数据,取均值。 图7 样机测试系统Fig.7 Experiment of the prototype 图8 20 Hz频率下幅值-电压关系Fig.8 Vibration amplitude-voltage under 20 Hz 其振幅均值随电压幅值的大小变化以及线性拟合直线如图8所示。当频率恒定时,输出幅值与电压幅值近似呈线性关系,拟合优度R2=0.997,具有很高的线性度。在输入电压幅值为200 V时,中心运动件具有105.5 μm的作动行程。 对作动器在不同电压下的振动幅值均取了5组数据,取其中40,80,120,160及200 V的重复试验数据,如表1所示,检验放大机构输出位移的稳定性。 表1 部分试验数据及标准差 由表1可以看出,经过多次测量,相同试验条件下不同幅值的正弦激励电压之下,中心运动部件的振动幅值只在很小的范围内浮动,作动器的动态性能很稳定。 测量单个叠层压电陶瓷在相同预紧力(50 N)下,在UA的驱动下产生的振动幅值,机构的放大效果如图9所示。可以看出,机构的输出位移与叠层压电陶瓷输入位移近似成正比关系,其斜率通过线性拟合得出为5.45,即放大倍数为5.45,相关程度为R2=0.999 5,具有很高的线性度。与有限元仿真得到的放大倍数5.71以及解析计算得到的5.76倍相对偏差分别为4.77%和5.69%。 图9 作动器放大效果Fig.9 Amplification effect 叠层压电陶瓷的频率响应特性影响着作动器的动态性能。采用上面的激励信号及试验装置,保持信号幅值大小为100 V,每10 Hz递增改变频率的大小,从10 Hz至300 Hz。通过激光位移传感器读取不同频率下的中心运动件的振动幅值,其随频率大小的变化如图10所示。试验结果表明,在频率升高的同时,输出振幅均匀缓慢减小。频率每升高10 Hz,输出振幅平均减小0.04 μm。 图10 100 V电压下幅值-频率Fig.10 Vibration amplitude- frequency under 100 V 压电叠堆输出位移与驱动电压之间存在多值对应的迟滞现象,了解驱动器的迟滞现象有助于实现作动器的快速、高精密定位。采用与前述试验相同的测试系统,在50 N预紧力的条件下,控制信号为三角波信号,其幅值为180 V,频率为20 Hz。测量叠层压电陶瓷和作动器的迟滞回线如图11所示。 图11 迟滞回线Fig.11 Hysteresis loop 由图11可以看出,作动器的迟滞回线、迟滞环最大宽度比由叠层压电陶瓷的11.45%变为放大机构输出的10.73%,迟滞曲线相比叠层压电陶瓷的迟滞曲线要光滑很多。同时迟滞环由叠层压电陶瓷的非中心对称迟滞环变为作动器的中心对称的迟滞环,作动器有双向对称的作动特性。 提出了一种利用三角形位移放大原理的新型双向压电作动器,分析了其工作原理,建立了理论和有限元静力模型。作动器所采用的放大机构区别于现有的通过弹性变形实现位移放大的机构,将叠层压电陶瓷产生的位移直接放大输出于作动件,位移放大效果与理论值、有限元仿真结果非常接近。样机试验表明:在幅值为200 V的正弦信号的激励下,行程达到105 μm,多组试验数据有很高的重复性;开环条件下,固定激励信号频率时,输出振幅与电压幅值呈线性关系,且有很高的线性度,拟合优度R2=0.997;当固定激励电压幅值时,驱动器的行程受激励频率影响较小,频率每升高10 Hz,作动振幅减小0.04 μm;放大机构的迟滞效应相比单个叠层压电陶瓷的迟滞效应有所改善,作动器迟滞回线为中心对称,具有双向对称作动特性。该作动器能够满足较大工作行程的高分辨率、双向对称主动驱动的驱动要求,适用于需要双向性能对称的精密作动及定位的场合。 [1] Tadigadapa S. Piezoelectric microelectromechanical systems-challenges and opportunities[J]. Procedia Engineering, 2010,5(2):468-471. [2] 赵淳生.超声电机技术与应用[M].北京:科学出版社,2007:534-551. [3] Callow D, Lee J, Blumenstein M, et al. Development of hybrid optimisation method for artificial intelligence based bridge deterioration model-feasibility study[J]. Automation in Construction, 2013,31:83-91. [4] 李会文,吴晖辉,胡俊峰.一种位移放大微动平台的设计和特性分析[J].机床与液压,2014(15):101-103. Li Huiwen, Wu Huihui, Hu Junfeng. Properties analysis and design of a dsplacement amplification micro-stage[J]. Machine Tool and Hydraulics, 2014(15):101-103. (in Chinese) [5] 靳宏,金龙,徐志科,等.压电叠堆位移放大致动器的动态特性[J].振动与冲击,2012,31(21):146-150. Jin Hong, Jin Long, Xu Zhike, et al. Dynamic characteristics of a piezoelectric-stack displacement-amplifying actuator[J]. Journal of Vibration and Shock, 2012,31(21):146-150. (in Chinese) [6] Lam K H, Wang X X, Chan H L W. Lead-free piezoceramic cymbal actuator[J]. Sensors and Actuators A: Physical, 2006,125(2):393-397. [7] 汪建新,刘曜宁,张玲聪,等.磁致伸缩换能器辐射板位移放大机构设计[J].机械设计与制造,2015(3):201-207. Wang Jianxin, Liu Yaoning, Zhang Lingcong, et al. Magnetostrictive transducer tadiating plate displacement magnifying mechanism design[J].Machinery Design and Manufacture,2015(3):201-207. (in Chinese) [8] Jiang Xin, Zhu Yuchuan. Mechanical amplifier for giant magnetostrictive materials and piezoelectric materials[J]. Hydromechatronics Engineering,2013,41(24):30-43. [9] Xu Qingsong, Li Yangmin. Analytical modeling, optimization and testing of a compound bridge-type compliant displacement amplifier[J]. Mechanism and Machine Theory,2011,46(2):183-200. [10] Zhou Huixing, Brian H. Analysis of a diamond-shaped mechanical amplifier for a piezo actuator[J]. International Journal Advanced Manafacturing Technology, 2007,32:1-7. [11] 黄卫清,史小庆,王寅.菱形压电微位移放大机构的设计[J].光学精密工程,2015,23(3):803-809. Huang Weiqing, Shi Xiaoqing, Wang Yin. Desigh of diamond piezoelectric micro displacement amplification mechanism[J]. Optics and Precision Engineering, 2015,23(3):803-809. (in Chinese) [12] Preumont A. Piezoelectric systems[M]. Borlin, Germany: Springer Netherlands, 2006:95-130. [13] Uchino K. Ceramic actuators: principles and applications[M]. Dittsbnrgy, United States: MRS Bulletin, 1993:42-48. [14] 闻邦椿.机械设计手册[M].北京:机械工业出版社, 2010:8-10. 10.16450/j.cnki.issn.1004-6801.2017.06.016 中航工业产学研资助项目(CXY2013NH09);国家自然科学基金资助项目(51375224);华侨大学高层次人才科研启动费资助项目(15BS102) 2016-02-25; 2016-04-14 TH112.5; TN384 刘雪瑞,女,1992年10月生,硕士生。主要研究方向为压电精密驱动技术。 E-mail:liuxr@nuaa.edu.cn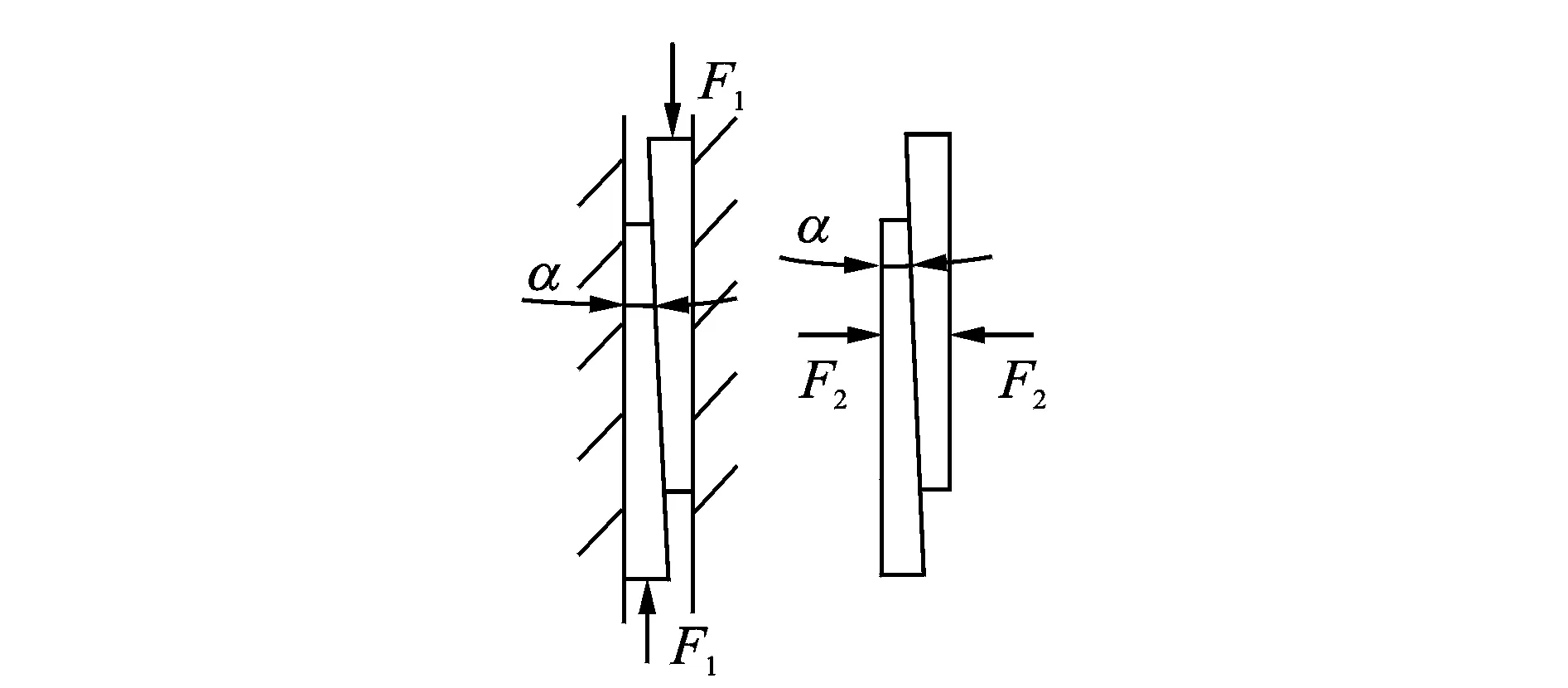
3 放大机构有限元静力分析
4 微位移放大机构的输出特性

4.1 输出幅值与电压的幅值的关系


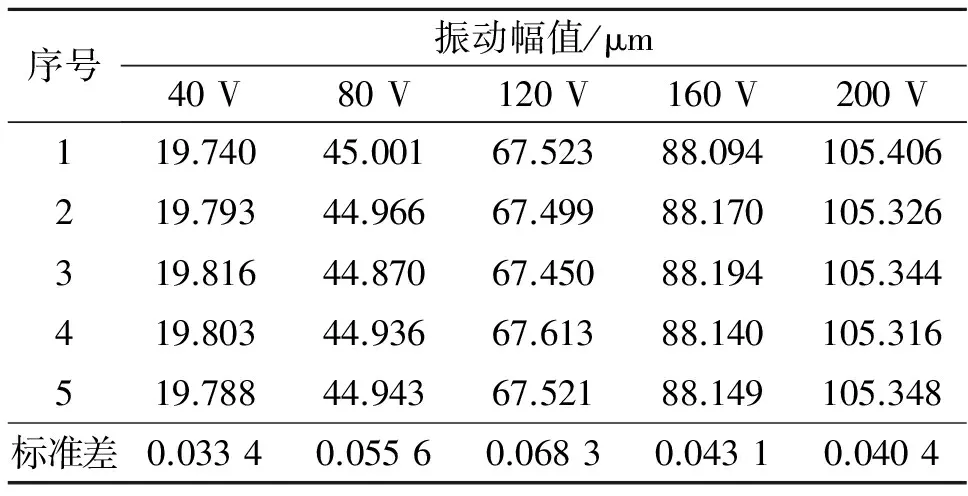
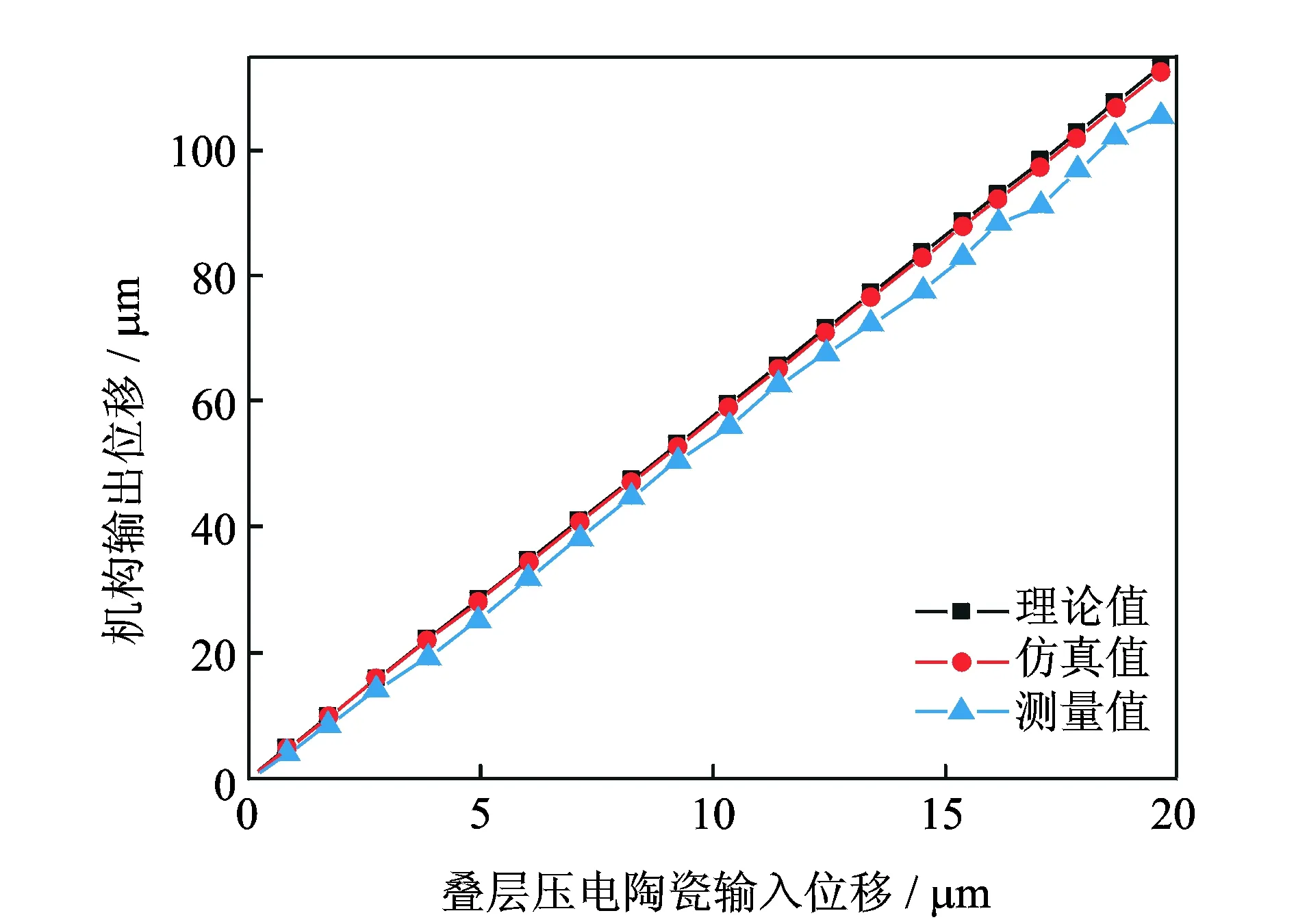
4.2 输出幅值的频率特性
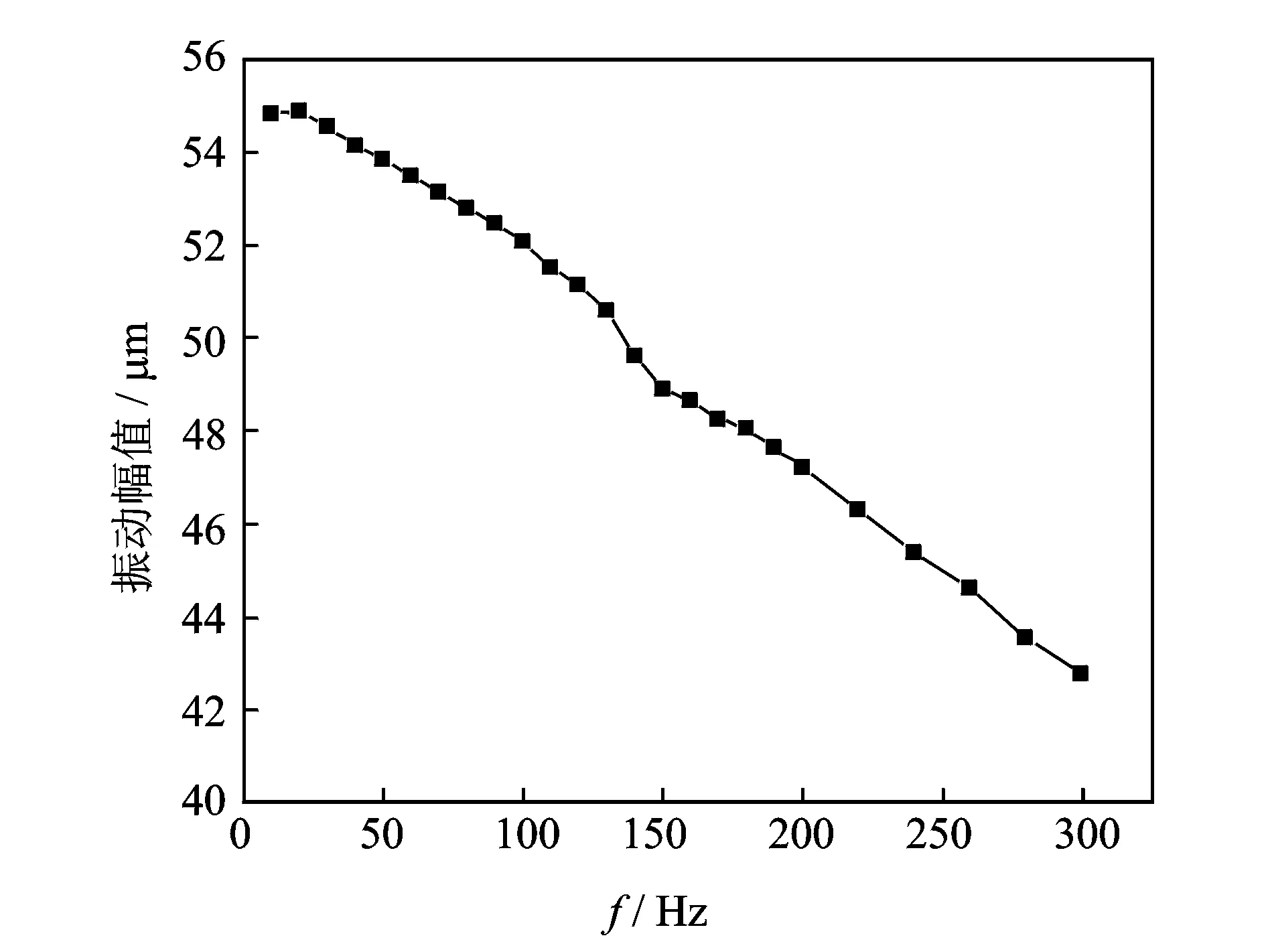
4.3 迟滞效应

5 结束语

