弹性体基础变形下的岸桥车梁耦合振动

2018-01-04童民慧王悦民邱惠清

振动、测试与诊断 2017年6期

关键词：大梁弹性体轮轨

童民慧，王悦民，邱惠清

(1．上海海事大学物流工程学院上海，201306) (2．同济大学机械与能源工程学院上海，201804)

弹性体基础变形下的岸桥车梁耦合振动

童民慧1,2，王悦民1，邱惠清2

(1．上海海事大学物流工程学院上海，201306) (2．同济大学机械与能源工程学院上海，201804)

为了研究弹性体基础变形下的岸桥高速小车轮轨耦合振动的问题，岸桥面对大型集装箱船进行装卸作业，其结构高耸庞大，前大梁横跨于集装箱船上方，具有的大跨度梁结构特点，起重小车在岸桥大梁的弹性体轨道高速往复运行，小车车轮与岸桥的大梁轨道发生轮轨接触，从而使得小车结构与岸桥结构产生耦合振动。根据小车-岸桥轨道耦合的动力学理论，建立岸桥的小车-大梁轨道的数学模型，选择合适的数值积分方法进行模拟计算，从而获得了小车振动以及客观存在的大梁轨道变形对小车轮轨之间的影响。在试验研究基础上对仿真研究的成果进行验证，包括岸桥在装卸工作过程中的结构应变、加速度和变形等数据，将实验采集到的数据与数值模拟计算得到的数据进行对比验证，分析得到岸桥高速耦合振动的规律，给出提高小车速度的措施。本研究以岸桥大跨度弹性体悬臂梁为基础，建立了大跨度弹性基础梁的车梁耦合动力学模型，找出小车与轨道系统垂向动力参数，得到各参数对轮轨动力作用的影响规律。

岸桥；车梁耦合；动力响应；耦合振动；弹性体基础变形

引言

随着航运业的快速发展，集装箱船舶运输的能力不断提高，对港口的吞吐能力、装卸技术提出了更高的要求。随着岸桥小车速度的不断提高，起升载荷不断增加，小车与岸桥的动力相互作用问题受到更多关注。岸桥是大跨度梁结构，高速小车在岸桥大梁的弹性体轨道运行，小车通过轮轨接触与岸桥结构形成耦合振动，高速小车运行时对岸桥结构产生冲击，对岸桥的工作状态和寿命产生影响，同时结构的振动又对运行小车的平稳性和安全性产生影响，这些成为评价岸桥结构动力设计参数的重要因素。对岸桥小车高速化发展具有非常重要的理论及工程实际意义。

笔者对岸边高速岸桥耦合振动和随机响应进行研究，探究高速岸桥的振动特性，并找出克服和减少振动的方法，为岸桥的高速发展提供理论基础和设计指导，对起重小车速度的提高、增加岸桥的装卸效率及解决大型岸桥小车高速问题有重要的意义。

1 岸桥特点

1.1 岸桥

岸桥是一种工作条件十分繁重的重型机械设备[1]。其载荷复杂多变，动态性质显著，整个岸桥的金属结构是关键部件。结构必须要满足总体要求，即工作幅度、跨度、前伸距、后伸距及起升高度等作业空间的要求；同时要考虑岸桥的结构必须安全可靠，具有足够的强度、刚度和稳定性。港口集装箱装卸专用设备岸桥是目前全世界各大港口装卸集装箱的主要设备[2]，具有结构大型化、载荷重载化、运行高速化、装卸高效化及专业化等特点。

1.2 岸桥车梁耦合振动理论

车梁耦合动力学属于工程应用针对性极强的技术学科，涉及车辆工程、轨道工程、振动力学、数值分析方法及计算机仿真技术等多个学科领域，学科交叉性强。研究这样复杂的问题，一般需要从理论模型、数值仿真和现场试验三方面入手，采用理论与试验相结合的研究方法，在实际工程中的具体应用则必须经过最终的现场试验来验证。

1.3 岸桥力学模型

由图1可以看出，岸桥装卸作业时，小车在岸桥大梁上运行[3]，而大梁由门框和拉杆多点支撑，形成多段简支梁结构(大梁最前端除外)。下面分别讨论不计质量的移动载荷(移动力)，即单个车轮(质量)以及单个车轮(簧下质量)+弹簧(阻尼器)+簧上质量通过简支梁时系统的分析模型、动平衡方程及其解的表达式，推导出小车-岸桥大梁耦合振动方程。

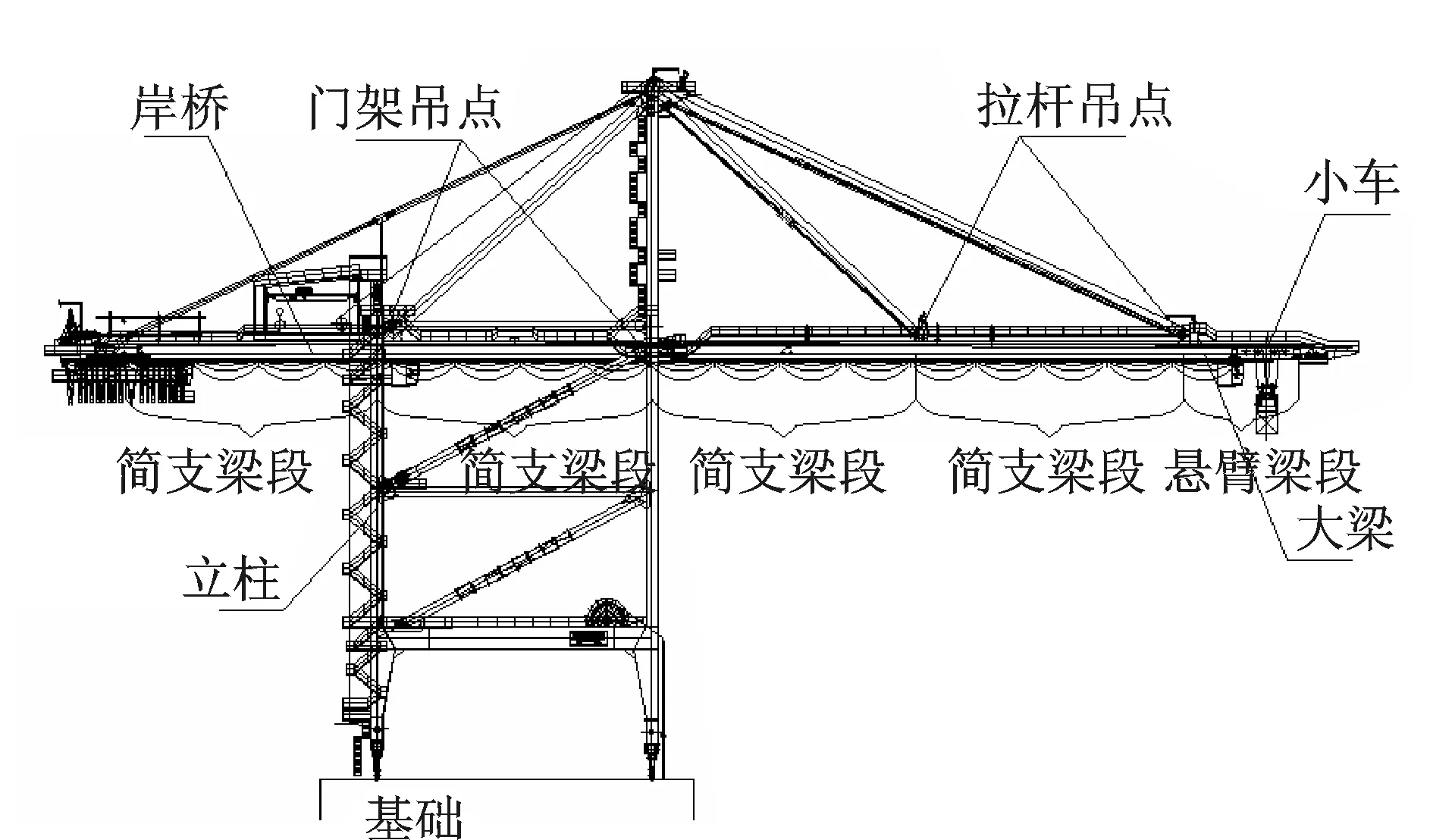
图1 岸桥小车在大梁上运行时产生的车-梁相互作用Fig.1 Interaction between trolley-boom in the container crane during running

1.4 简支梁在移动质量作用下的振动

对于简支梁，如果移动载荷的质量与梁的质量相比不能忽略，就必须同时考虑载荷的重力作用以及随梁一起振动时产生的惯性力，而简化成为图2所示的模型。考虑一个车轮通过岸桥的情况，车轮质量假定沿梁长移动而不脱离梁体，则其位移与它所在位置的梁的挠度是一致的。

图2 移动质量作用下的简支梁模型Fig.2 The mechanics model of simple supported girder by moving load

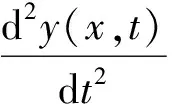
(1)

移动载荷质量的简支梁耦合动力平衡方程为

(2)

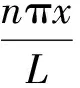
(3)

对于简支梁，如果位移级数中取N项，则整个简支梁的自由度将从无穷多个减少到N个，系统运动方程的N阶矩阵表达式[4]为

(4)

其中：q为广义位移向量，q=[q1,q2,…,qn]T；F为广义力向量，F=[ρFφ1,ρFφ2,…,ρFφN]；M为广义质量矩阵。

其中：C为广义阻尼矩阵；K为广义刚度矩阵。

C，K均为对角矩阵

2 岸桥大梁弹性体轨道下的小车车梁耦合振动

岸桥的大梁是弹性体轨道，小车车轮在弹性体轨道上高速运行，轮轨接触产生的动力相互作用对岸桥结构产生耦合振动[5]。小车-岸桥的车梁耦合振动的研究方法如下：首先，建立起小车-岸桥的耦合模型；然后，对耦合模型进行求解，得到振动的位移、速度和加速度，从而得到振动的各项参数[6]。

小车高速运动对岸桥产生动力冲击作用，直接影响其工作寿命；岸桥的振动又对小车的平稳性和安全性产生影响。采用理论分析、数值模拟的方法，对高速岸桥的动力特性进行研究，具体结果[7]如下。

由图3结果可以看出，小车满载从最大前伸距开始由海侧向陆侧运行，接着反向从陆侧向海侧运行，最后制动至停止整个过程[8]，垂向位移变化的情况如下：大梁最前端的垂向位移先增至最大，然后逐渐减小，运行至门框中卸箱位置时，垂向位移最小；接着小车折返运行，垂向位移逐渐增大，当运行至最大前伸距制动并停止，垂向位移逐渐稳定在一个恒定值；而大梁最后端的垂向位移变化正好相反；大梁跨中的位移变化趋势与大梁最前端类似，但位移值相对较小[9]。

图3 小车速度为4m/s时大梁的垂向位移振动曲线Fig.3 Vertical vibration curve of girder during trolley′s speed 4 m/s

由图4结果可以看出，小车满载从最大前伸距开始由海侧向陆侧运行，接着反向从陆侧向海侧运行，最后制动至停止整个过程，纵向位移变化的情况如下：大梁最前端的纵向位移先增至最大，然后逐渐减小，运行至门框中卸箱位置时，纵向位移最小；接着小车折返运行，纵向位移逐渐增大，当运行至最大前伸距制动并停止，纵向位移逐渐稳定在一个恒定值[10]；而大梁最后端及大梁跨中的位移变化趋势与大梁最前端类似，但位移值相对较小。

图4 小车速度为4m/s时大梁的纵向位移振动曲线Fig.4 Longitudinal vibration curve of girder during trolley′s speed 4 m/s

由图5结果可以看出，小车满载从最大前伸距开始由海侧向陆侧运行，接着反向从陆侧向海侧运行，最后制动至停止整个过程，横向位移变化的情况如下：大梁最前端的纵向位移先增至最大，然后逐渐减小，运行至门框中卸箱位置时，横向位移最小；接着小车折返运行，横向位移逐渐增大，当运行至最大前伸距制动并停止，横向位移逐渐稳定在一个恒定值；而大梁最后端及大梁跨中的位移变化趋势与大梁最前端类似，但位移值相对较小。

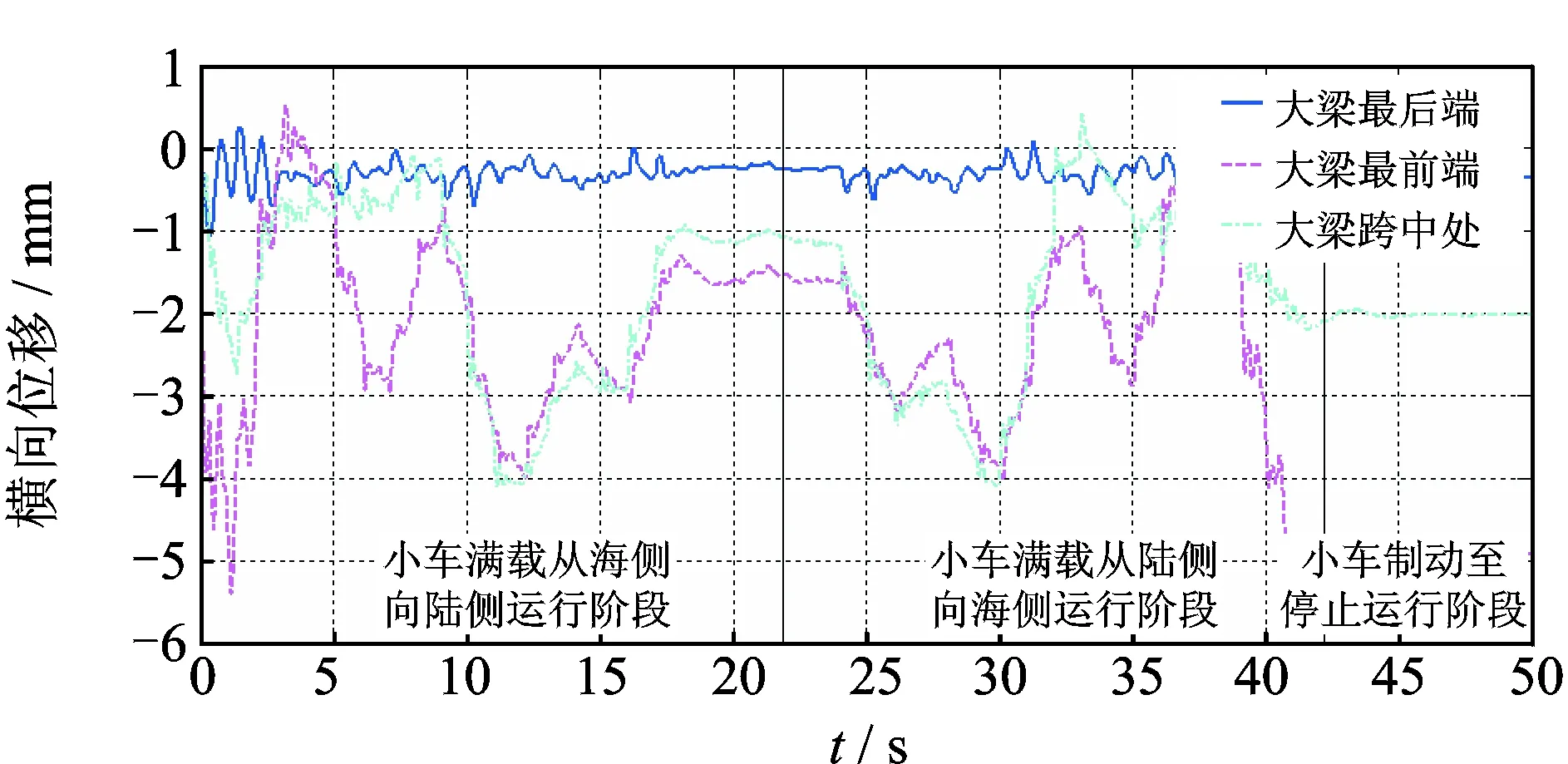
图5 小车速度为4m/s时大梁的横向位移振动曲线Fig.5 Transverse vibration curve of girder during trolley′s speed 4 m/s

小车不同速度下的结构响应比较如图6～图9及表1所示。

图6 不同小车速度下岸桥大梁头部垂向位移时程曲线Fig.6 Vertical vibration curve of girder during trolley′s varying speeds

图7 不同小车速度下岸桥大梁头部纵向位移时程曲线Fig.7 Longitudinal vibration curve of girder during trolley′s varying speeds

图8 不同小车速度下岸桥大梁头部横向位移时程曲线Fig.8 Transverse vibration curve of girder during trolley′s varying speeds

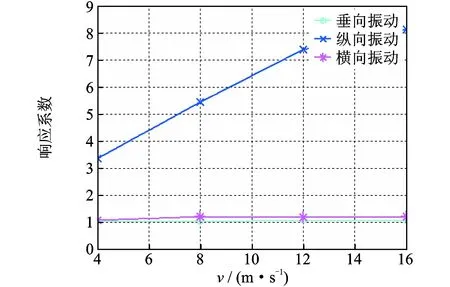
图9 不同小车速度三个方向的响应系数比较曲线Fig.9 Comparison of three directions response factors during trolley′s varying speeds

从上述计算结果可知，随着小车速度增加，岸桥结构振动响应不断增加，小车运行方向的纵向响应明显，垂向与横向响应略有增加，说明小车在岸桥上运行时，速度增加对岸桥结构的纵向影响大。通过在岸桥上布置加速度传感器，测出真实的岸桥振动，测点如图10～图12所示。

表1 小车速度与大梁前端振动响应的关系

图10 大梁最前端振动加速度测点Fig.10 The acceleration test point on the boom tip

图11 大梁跨中振动加速度测点Fig.11 The acceleration test point on the boom middle

图12 测点布置示意图Fig.12 Arrangement figure of test points

测试工况如下：

1) 调零状态，即载荷置于地面上，钢丝绳放松；

2) 小车吊起试验载荷，并全速运行到前大梁最外端，载荷下降后制动，全速上升后制动，结构振动至基本平稳；

3) 小车运行至前拉杆铰点位置，载荷下降后制动，全速上升后制动，结构振动至基本平稳；

4) 小车运行至前拉杆与前中拉杆跨中位置，载荷下降后制动，结构振动至基本平稳；

5) 小车运行至前中拉杆铰点位置，载荷下降后制动，结构振动至基本平稳；

6) 小车运行至前中拉杆与大梁铰点跨中位置，载荷下降后制动，结构振动至基本平稳；

7) 小车运行至后大梁门框跨中位置，载荷下降后制动，结构振动至基本平稳；

8) 系统回零，检查测试系统是否正常。

根据图13所示的实测数据，与模拟计算比较，大梁最前端垂向加速度在起升时最大，小车水平运行时，加速度相对较小，这与模拟计算的结果一致。大梁最前端横向加速度在起升时也是最大，小车水平运行时，加速度相对较小[11]。实测数值比模拟计算的结果略小，说明模拟计算的结果偏于保守。

图13 岸桥实测加速度曲线Fig.13 The acceleration testing curve on the real container crane

3 结论

1) 研究高速小车-岸桥轨道耦合振动规律，岸桥的高速化导致小车与大梁之间的相互动力作用问题，直接影响着岸桥的安全与效率。对高速小车岸桥耦合振动及随机响应进行研究，找出了高速岸桥的振动特性，小车运行在轨道上，来自轨道的激扰使车辆产生振动，反过来又使轨道产生振动，二者处于相互耦合的振动状态。通过对小车与轨道系统垂向动力参数的研究，综合评价轮轨间的垂向动力作用，总结出各参数对轮轨动力作用的影响规律。

2) 利用车梁耦合法对有限元计算得到的响应数据，分析大梁轨道变形引起的振动特点，寻找减轻有害振动的措施。大梁轨道变形也是引起结构振动的原因，引起高速小车与结构振动。以大梁轨道变形作为基础，小车在弹性梁上运行，由于岸桥大梁是大跨度梁结构，在小车动载运行下，会发生较大振动与变形，而小车通过固定于大梁上的轨道，在大梁上运行，所以大梁的晃动及大跨度变形会产生很大影响。小车在大梁上的正常运行，这样小车的振动和岸桥大梁的结构振动互相作用，相互影响，形成耦合振动问题。岸桥小车的基础为弹性梁，以大跨度悬臂梁作为基础，建立了大跨度弹性基础梁的车梁耦合动力学模型。

[1] 蒋国仁.岸边集装箱起重机[M]．武汉：湖北科学技术出版社，2001：25-29.

[2] 中华人民共和国国家标准局. GB3811—2008 起重机设计规范[S]. 北京：中国标准出版社，2008.

[3] 卢凯良, 张卫国, 吴志君, 等. 集装箱起重机减隔震装置及其模型试验[J].振动、测试与诊断,2011,31(4):501-506.

Lu Kailiang, Zhang Weiguo, Wu Zhijun, et al.Anti-seismic device design for container crane and its model test[J]. Journal of Vibration, Measurement & Diagnosis , 2011,31(4):501-506. (in Chinese)

[4] 邱惠清,卢凯良,李雪,等. 岸桥前大梁铰支座支承对其横向振动的影响[J].振动、测试与诊断,2009, 29 (3): 299-302.

Qiu Huiqing,Lu Kailiang,Li Xue, et al. Influence of support means of hinge-bearing for container crane′s boom on lateral vibration[J].Journal of Vibration, Measurement & Diagnosis ,2009, 29 (3):299-302. (in Chinese)

[5] 翟婉明. 车辆-轨道耦合动力学[M].3版. 北京：科学出版社, 2007:4-11.

[6] 曾宇清.车桥(轨)耦合振动系统仿真中的基本问题、解决办法及其应用范围[J].中国铁道科学，2002,23(4): 12-17.

Zeng Yuqing. Vehicles-bridge (rail) coupling vibration system simulation of the basic problems, solution and application scope[J]. China Railway Science，2002,23(4):12-17. (in Chinese)

[7] 唐友刚．高等结构动力学[M]．天津：天津大学出版社，2002:121-126.

[8] 夏禾. 车辆与结构动力相互作用[M]. 北京：科学出版社, 2002:144-149.

[9] R.W.克拉克J，彭津.结构动力学[M]. 王光远,译. 北京：科学出版社，2002:46-52.

[10] 张国瑞.有限元法[M]. 北京：机械工业出版，1991:19-23.

[11] 童民慧. 超巴拿马双小车集装箱岸桥钢结构动力响应研究[D].上海：上海海事大学，2004.

10.16450/j.cnki.issn.1004-6801.2017.06.010

国家高技术研究发展计划(“八六三”计划)资助项目(2009AA043000)

2015-09-15；

2015-11-23

TH113.1