基于流形学习的SAR图像目标分类∗

彭易锦

（中国电子科技集团公司第十研究所 成都 610036）

基于流形学习的SAR图像目标分类∗

彭易锦

（中国电子科技集团公司第十研究所 成都 610036）

提出一种基于流形学习的SAR图像特征降维和目标分类方法，该方法包含以下三个步骤：1）提取SAR图像目标的高维特征向量；2）采用基于流形学习的方法提取嵌入在高维特征向量中目标的本征维特征；3）利用本征特征进行目标分类。实验结果表明，论文方法在利用较少维数特征的条件下，得到了与利用全部特征时相当的目标分类精度，证实了论文方法是有效的。

流形学习；目标分类；SAR图像；特征提取

1 引言

目标分类是SAR图像解译和分析的重要组成部分，是国内外图像处理和模式识别领域的研究热点，广泛应用于国防和民用的诸多领域。目标分类的一种典型研究思路是从大量包含目标的数据中学习并抽取目标特征，并采用统计分类技术进行目标分类识别［1］。

图像目标的特征有很多种，常用的有灰度特征、统计特征、纹理特征、形状结构特征等［2～3］。为了实现特定的图像分析和解译任务，通常的做法是先提取各种图像特征，并组成特征向量。这种方法存在以下两个问题：1）所提取的图像特征向量通常都位于维数较高的空间，直接对这些数据进行处理，会出现所谓的“维数灾难”问题，巨大的计算量是无法忍受的；2）高维特征向量通常没有反映出图像的本质特征，存在大量无用信息，直接对这种特征向量进行处理，难以得到理想的结果。针对这一问题，普遍的做法是，对高维数据作维数约减处理，从中提取低维空间中的本征特征。

如何将高维数据表示在低维空间中，并由此发现反映其内在结构的低维数据是高维信息处理研究的关键问题之一。维数约减的基本原理是把数据样本从高维输入空间通过线性或非线性映射投影到一个低维空间，从而找出隐藏在高维观测数据中有意义的低维结构。从几何的观点来看，降维可以看成是挖掘嵌入在高维数据中的低维线性或非线性流形。这种嵌入保留了原始数据的几何特性，即在高维空间中靠近的点在嵌入空间中也相互靠近。最近兴起的流形学习方法是一种线性降维的方法，并且依靠它们在探测嵌入在高维空间中低维流形的能力和灵活性而被广泛应用。具有代表性的流形学习算法包括线性方法中的主成分分析（PCA）、线性判别分析（LDA），非线性方法中的等距映射（Isomap）、核主成分分析（KPCA）、局部线性嵌入（LLE）、拉普拉斯特征映射（LE）等［4～8］。

本文着眼于SAR图像目标的分类，首先提取SAR图像目标的高维特征向量，然后对其进行维数约减提取本征特征，并基于所提取的本征特征进行目标分类识别。

2 图像特征

图像特征是指图像中可用作标志的属性，其中有些是直觉感受到的自然特性，有些需要通过变换或测量才得到的人为特征。常见的图像自然特征有亮度、色彩、纹理以及轮廓等；认为特征有灰度直方图特征、投影特征、标记、Fourier描述子、矩特征、比例特征、线条特征等。通过图像的这些特征，还可以得到如角点、顶点、边缘、边界、形状等结构特征［9］。

SAR图像的特征提取是SAR图像解译和分析的重要步骤，通过特征提取可以有效地降低数据空间的维数，从而达到快速、准确地对SAR图像解译的目的。实际应用中，为了实现SAR图像的解译，通常提取灰度统计特征、纹理特征以及形状结构特征等。为了验证本文算流形学习算法以及分类方法的有效性，本文提取了灰度直方图特征、Gabor纹理特征以及LBP直方图特征［10～11］。

3 流形学习

流形学习本质上是一个维数约减的过程，假设数据是均匀采样于一个高维欧氏空间中的低维流形，流形学习就是从高维采样数据中恢复出低维流形结构，找到内蕴在高维空间中的低维流形，并求出相应的嵌入映射，以实现数据的维数约减，即从观测到的现象中去寻找事物的本质，找到产生数据的内在规律［4～8，12］。流形学习的数学定义可以描述如下：

给定观测数据集X={x ，i=1，…N }∈RD，假

i设X中的数据样本是由低维空间中的数据集Y={ yi，i=1，…N }∈Rd，通过某个未知的光滑映射f所产生，其中d≪D，则流形学习的任务是基于给定的观测数据集X：

1）恢复出低维表示；

2）构造从高维观测空间到低维空间的光滑映射：f-1:RD→Rd。

从定义可以看出，流形学习的基本假设是一个位于高维观测空间中的数据集有其内蕴的低维流形结构，流形学习的目的在于：在保持原始数据集某种结构不变的准则下，从观测到的高维数据中恢复出其低维流形表示并得到相应的映射，从而抓住数据的本质规律。

根据流形学习技术对数据基本假设的不同，可以将其分为线性流形学习技术和非线性流形学习技术。线性流形学习技术通常假设数据位于一个全局线性结构中，在这种假设前提下，只需找到一个显式的线性映射便可来实现数据从高维观测空间到低维本征空间的降维过程，常见的线性流形学习技术如PCA方法、LDA方法等。非线性流形学习技术通常假设数据位于一个局部线性，全局非线性的流形曲面上，要实现对原始高维数据的维数约减，就需要在保持原始数据某种拓扑结构在降维后不变的准则下，对数据进行非线性映射，常见的非线性流形学习技术如Isomap、KPCA、LLE、LE 等［4～8，12］。

非线性流形学习方法与线性方法相比的一个显著特点是，分析中的局部性，原因在于对数据集合的内蕴结构而言，有下列特性：

1）由泰勒定理，任何可微函数在一点的充分小的邻域之内满足线性性。形象的来讲，相当于认为曲面流形可由大小不一的局部线性块拼接而成；

2）数据流形经常是由许多可分割的子流形所组成；

3）数据流形的本征维数沿着流形不断的发生变化，只有局部性才能抓住其根本特性。

由于现实问题通常是非线性的，实际应用中，非线性流形学习方法的处理结果往往优于线性方法的处理结果。

由于真实自然数据通常表现为复杂的高度非线性结构，因此全局线性的假设通常不再适用，这时就需要采用非线性流形学习技术。由于篇幅限制，本文只就其中的PCA方法和LE技术作简单介绍。

3.1 主成分分析（PCA）

PCA技术将数据方差的大小作为衡量信息量多少的标准，方差越大则提供的信息越多，方差越小则提供的信息越少。基于这一判断依据，PCA技术通过线性变换保留数据中方差大、信息量多的分量，而丢掉方差小、信息量少的分量，即只用少数几个最主要的分量来表达数据，从而达到降维的目的。PCA技术可以描述为如下几个步骤：

1）求取数据集 X={xi，i=1，…N}∈RD的协方差矩阵：

2）按式（1）对协方差矩阵作特征值分解，其中U是由特征矢量构成的正交矩阵，Λ=diag(λ1，…，λD)是由特征值构成的对角矩阵，且λ1≥…≥λD：

3）选取前d个较大特征值对应的特征向量构成投影矩阵U0

4）将原始数据集按下式投影至由U0T张成的线性子空间上即得到d维特征向量

3.2 拉普拉斯特征映射（LE）

LE技术将微分流形、谱图论的知识应用于降维之中，使人们对降维过程的认识产生了又一个新的飞跃，拓展了实际中降维方法的应用，其基本思想是：在高维空间中距离相隔很近的点投影到低维空间中像也应该相距很近，最终求解归结到求拉普拉斯算子的广义特征值问题。。该技术的算法描述如下：

1）构建邻接图G：在高维观测空间中，求每个数据点 xi的k邻域Ji；

2）构建加权邻接图W：对邻接图G加权得到加权矩阵W，其中t是一个比例参数：

3）特征映射：计算d维嵌入。假设y=(yi，…，yN)T是一个未知的投影，可以通求解如下的目标函数最小得到

用D表示对一个对角矩阵，它的每个对角元素为矩阵W的每行所有元素的和，即L=D-W是邻接图的Laplacian矩阵。对任意的y有下式成立：

可以将该最优化问题转化为对Laplacian矩阵的广义特征值分解：

她穿过客厅，走到阳台上，这个阳台，是最佳的观景处，想必爸爸当年也是站在这样的位置看见这样的风景吧？春天时风摆杨柳、夏天时碧云满天、秋天时秋月扬辉……冬天时……冬天时，冬岭秀孤松……

假设前d+1个最小特征值对应的特征向量为u，…，u，那么 X的低维嵌入表示为 y=，2d+1ii进而得到低维本征空间Rd中的数据集Y={ yi，i=1，…，N } 。

从LE算法的描述可以看出，它的准则在于保持数据的局部距离结构信息，将在原始高维观测空间中离得近的点在映射后拉得更近，它隐式地体现了数据集自然聚类效果。另外，在分类问题中，通常离得较近的点属于同一类别的概率较大，因此LE技术也适合分类问题中的维数约减。

4 分类方法流程

为了验证流形学习方法的性能，本文设计如图2所示的分类方法流程。首先，分别提取训练图像和测试图像的多种特征，并分别组成特征向量；然后，利用第3部分介绍的流行学习方法对提取的特征向量进行维数约减，得到本征特征；最后，利用本征特征对图像目标分类。

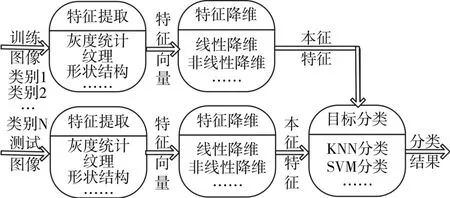
图1 分类方法流程

5 实验及结果分析

为了验证流形学习算法的性能以及上述方法流程在图像目标分类中的有效性，本文在真实SAR图像上进行实验。

图2 各类目标的样本示例

5.1 实验数据

实验数据为TerraSAR卫星获取X波段SAR图像，获取时间为2008年5月24日，距离向和方位向的分辨率均为1.25m，包含五类地物的目标样本，分别为河流、湿地、耕地、建筑和山地，样本大小为128像素×128像素，各类别的样本数分别为204个、379个、340个446个和387个，图2是各类目标的样本示例。

5.2 实验结果及分析

实验中提取的特征包括三种：灰度直方图（图像为16位数据，分成128个灰度阶得到128维特征）、Gabor滤波器组（不同尺度、不同方向滤波器组，得到40维特征）和LBP特征（统计LBP直方图，得到32维特征）。

为了说明各维特征的有效性，本文采用判别数作为客观评价指标［13］。判别数J可由下式表示

其 中 ，Sb=(xˉi-xˉ)2表 示 类 间 离 散 度 ，S=σ表示类内离散度，xˉ为第 i类的均值，xˉwii为总体均值，σi为第i类的样本方差。J值越大，则表示特征所携带的信息量越丰富，类别可分性也越好。

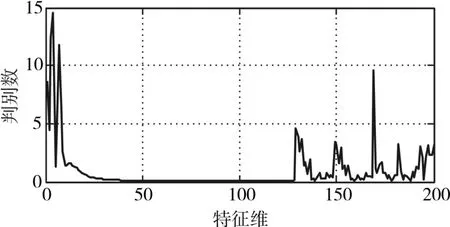
图3 不同特征的判别数

为了直观地展现特征的类可分性，图4画出了上述判别数较大的六维特征对应的散点图。由图可以看出，各维特征、不同类别之间均存在较大程度的重叠。

以上实验结果说明两点：1）高维特征向量存在冗余或无效信息；2）高维特征具有非线性特性。直接利用这种数据进行分类识别，难以得到理想的处理结果。因此，有必要对高维特征向量作降维处理。本文选择非线性流形学习方法Laplacian特征映射对高维特征向量作降维处理。为了说明非线性流形学习方法的优越性能，实验中同时也实现了经典的PCA线性降维方法，以便对比。

实验中，分别采用PCA降维和Laplacian特征映射方法对所提取的200维特征向量作降维处理，并得到维数为10的本征维特征，图5是其中三维特征的散点图分布情况。由图5可以看出，与原特征相比，降维后的特征类间离散度更大、类内聚集性更好，这一结果直观上说明了特征降维对目标分类识别的有效性。

图4 降维前特征的散点图（a）第3，4，7维特征的散点图（b）第129，149，169维特征的散点图

图5 降维后特征的散点图（a）PCA降维后其中三维特征的散点图（b）LE降维后其中三维特征的散点图

为了进一步客观地说明特征降维的有效性，本文在SAR图像样本数据上进行分类实验，分别利用原始200维特征、PCA降维和Laplacian特征映射后的10维本征特征对样本分类。本文采用K近邻（KNN）分类方法［14～15］，它是—种最基本的基于实例的方法，以其简单、有效和高鲁棒性而被广泛地应用于机器学习与数据挖掘领域解决分类问题。其分类思想是：给定一个待分类的样本x，首先找出与x最接近的或最相似的k个已知类别标签的训练集样本，然后根据这k个训练样本的类别标签确定样本x的类别。该方法不对特征作优化处理，更能反映特征本身的有效性，这也是选择该方法的重要原因。

实验中的参数设置如下：近邻数K=11，每类的训练样本数为100个，其中，训练样本是随机选择的，并独立重复10次实验，分类精度为10次实验结果的平均值。

实验结果如表1所示。由表1可以看出，利用原始200维特征的分类方法的平均分类精度为96.4%，利用由PCA方法得到的10维特征的分类方法的平均精度为87.6%，有较大程度的精度下降；而利用由流形学习方法得到的10维本征特征的分类方法的平均分类精度为95.1%，很好地保持了分类精度。本次实验结果表明：1）Laplacian特征映射方法能够较好地提取嵌入在高维数据中的本征维特征；2）非线性流形学习方法较线性方法，在实现数据降维的同时，能更好地保留高维数据的内在结构。3）数据降维是以牺牲一部分信息为代价的，PCA方法和Laplacian特征映射方法都存在一定程度的信息损失。

表1 目标分类精度对比

6 结语

本文提出了一种基于流形学习的SAR图像目标分类方法，该方法在提取SAR图像目标的高维特征向量后，通过流形学习降维得到嵌入在高维特征向量中的本征特征，并在TerraSAR图像上进行分类实验，分类准确率达到了95.1%。本次实验的结果表明，SAR图像目标的高维特征中存在较大程度的信息冗余，这些信息不仅需要较大的存储空间，而且会提高计算复杂，不适合直接用于目标分类，需要进行特征的维数约减；基于拉普拉斯特征映射的流行学习方法，能在大幅度实现特征降维的同时，较好地提取本征特征，其在SAR图像目标分类实验中的分类性能明显优于PCA方法。因此，本文提出的方法是有效的，在目标分类识别应用中具有一定的理论意义和应用价值。

［1］D.Lu and Q.Weng.A survey of image classification meth⁃ods and techniques for improving classification perfor⁃mance［J］.International Journal of Remote Sensing，2007，28（5）：823-870.

［2］王润生.图像理解［M］.长沙：国防科技大学出版社，1995.WANG Runsheng.Image Understanding［M］.Changsha：Press of National Defense University of Science and Tech⁃nology，1995.

［3］陈宏.基于形状特征的图像检索［D］.西安：西安电子科技大学，2010.CHEN Hong.Image Retrieval Based on Shape Feature［D］.Xi'an：Xidian University，2010.

［4］Shangtan Tu，Jiayu Chen，Wen Yang，Hong Sun.Lapla⁃cian Eigenmaps-based Polarimetric Dimensionality Re⁃duction for SAR Image Classification［J］.IEEE Trans.Geosci.Remote Sens.，2012，50（1）：170-179.

［5］L.J.P.van der Maaten，E.O.Postma，and H.J.van den Herik.Dimensionality reduction：A comparative review［R］.Tilburg Univ.，Tilburg，the Netherlands，Tech.Rep.TiCC-TR 2009-005，2009.

［6］H.Hotelling.Analysis of a complex of statistical variables into principal components.Warwick&York，Inc，1933.

［7］M.Belkin，P.Niyogi.Laplacian Eigenmaps and spectral techniques for embedding and clustering［M］.Advances in Neural Information Processing Systems，Cambridge，MA，USA：MIT Press，2002，14：585-591.

［8］J.B.Tenenbaum，V.de Silva，J.C.Langford.A global geo⁃metric framework for nonlinear dimensionality reduction［J］.Science，2000，290（5500）：2319-2323.

［9］鲍文霞.基于结构特征的图像匹配算法及应用［D］.合肥：安徽大学，2010.BAO Wenxia.Image Matching Algorithm Based on Struc⁃ture Feature and Its Application［D］.Hefei：Anhui Univer⁃sity，2010.

［10］薛玉利.基于Gabor变换的特征提取及其应用［D］.济南：山东大学，2007.XUE Yuli.Gabor Transform-Based Feature Extraction and Its Application［D］.Jinan：Shandong University，2007.

［11］Ahonen T，Hadid A，Pietikainen M.Face description with local binary patterns：Application to face recognition［J］.IEEE Trans.on PAMI，2006，28（12）：2037-2041.

［12］H.Seung，D.Lee.The manifold ways of perception［J］.Science，290（2000）2268-2269.

［13］骆玉霞，陈焕伟.遥感图像的特征提取与选择研究［J］.信息记录材料，2002，3（2）：22-26.LUO Yuxia，CHEN Huanwei.Research on Feature Ex⁃traction and Selection of Remote Sensing Image［J］.In⁃formation Recording Materials，2002，3（2）：22-26.

［14］豆增发，王英强，王保保.一种基于信息增益的K-NN改进算法［J］.计算机工程与应用，2007，43（19）：52-56.DOU Zengfa，WANG Yingqiang，WANG Baobao.An Im⁃proved KNN Algorithm Based on Information Gain［J］.Computer Engineering and Applications，2007，43（19）：52-56

［15］张莹.基于自然最近邻居的分类算法研究［D］.重庆：重庆大学，2015.ZHANG Ying.Research on Classification Algorithm Based on Natural Nearest Neighbors［D］.Chongqing：Chongqing University，2015.

Manifold Learning-based SAR Image Target Classification

PENG Yijin
（China Electronics Technology Group Corporation No.10 Research Institute，Chengdu 610036）

A manifold learning-based approach is proposed for dimension reduction and target classification of SAR image.This approach includes three steps：1） Extracting high-dimensional feature vector of SAR image target；2） Manifold learn⁃ing-based innate character extracting from the high-dimensional feature vector；3）Target classification using the innate character.The experimental result indicates that the proposed approach obtain relatively high accuracy of target classification in the case of us⁃ing low-dimensional feature compared to the high-dimensional feature vector，which proves the effectiveness of the proposed ap⁃proach.

manifold learning，target classification，SAR image，feature extraction

Class Number TP753

TP753

10.3969/j.issn.1672-9722.2017.12.035

2017年6月9日，

2017年7月28日

国家自然科学基金项目（编号：61501178）资助。

彭易锦，男，博士，工程师，研究方向：机器学习、情报处理、信息融合、目标识别等。