带领导者和不同时滞的多无人机系统编队控制∗

邵俊倩 李成凤 孙 剑

（绥化学院信息工程学院 绥化 152061）

带领导者和不同时滞的多无人机系统编队控制∗

邵俊倩 李成凤 孙 剑

（绥化学院信息工程学院 绥化 152061）

基于多智能体系统时滞一致性理论，对有领导者和不同时滞的多无人机系统编队控制问题进行研究，改进了系统的控制协议，使多无人机系统在获得很少信息的情况下就能实现一致。在变拓扑网络结构下，采用时域LMI方法得到不同时滞二阶多无人机系统达到一致的充分条件，通过解线性矩阵不等式得到了时滞的最大容许值。进一步，对无人机间通信时滞和无人机与领导者间通信时滞相同的情况加以讨论，并通过仿真实验验证了控制器设计的有效性。

多无人机系统；通信时滞；控制器；一致性理论

1 引言

多智能体系统的时滞一致性理论由于其应用的广泛性，已受到诸多专家学者的关注，成为多智能体系统协调控制的研究热点之一［1］。然而，对于时滞一致性来说，其研究历史相对较短。Olfati-Sa⁃ber等［2］在2004年首次对动态系统的时滞一致性问题进行了建模，通过频域分析法，获得了传输为单常时滞的多智能体系统实现一致性的充要条件。2005年，Bliman［3］等进一步对时变时滞及多时滞问题进行研究，得到了单时变时滞情况下的充要条件及多时变时滞情况下的充分条件。由于处于时滞一致性研究的初期，上述研究的智能体系统模型均为一阶积分器。然而，从控制一致性的角度来看，二阶积分器模型较一阶积分器模型能更精确地刻画系统的动态［1］。早在 2005年，Ren［4］等就对无通信时滞二阶积分器型智能体系统一致性进行了理论研究，但是，对于有时滞的一致性问题，直到2007年，Lin等才对固定拓扑下的常时滞二阶多智能体系统的一致性进行了研究［5］。对二阶多智能体系统一致性问题的研究，真正意义上地将代数图论与动力学理论有机地结合起来，为一致性理论的研究与发展奠定了基础。针对二阶多智能体系统的时滞一致性，人们同样进行了大量的研究，并取得了丰硕的成果［6～14］。

虽然，在文献［6］中对具有随机时滞的多智能体系统的一致性进行了研究，但在控制器的设计上有一些局限。本文将文献［6］中的控制器加以改进，把智能体具体化为无人机，研究有领导者和不同时滞的二阶多无人机系统的一致性控制。在变拓扑网络结构下，采用时域LMI方法对不同时滞多无人机系统进行研究，通过解线性矩阵不等式得到时滞的最大容许值。

2 图论基础

有向图 G(V，E，A)包含 n 个节点，其中V={e1，e2，…，en}为节点集，E⊆V×V 为图G 的边集，其元素eij=(i，j)∈E称为图G的边，边的权值矩阵为 A=[aij]称为邻接矩阵，其中 aij≥0(i≠j)，aii=0。图G的节点在集合 I={1，2，…，n}中取值。如果这个有向图满足aij=aji(i，j∈I)，则图G称为无向图。节点ei的邻集可以记为Ni={ej∈V:(ei，ej)∈E}，图 G 的Laplacian矩阵为 L=(lij)，其中。如果存在一个节点使得任意节点到这个节点都有有向路径，则称有向图是强联通的。

引理1：设 L是有向图G的Laplacian矩阵，则L有一个零特征值，其余n-1个特征值全部具有正实部。特别的，若G是无向图，它的特征值全是正实数。

3 系统模型

考虑由 n+1个无人机 e0，e1，…，en构成的多无人机系统，其中节点e0代表领导者且为全局可达点，其它节点 e1，e2，…，en代表跟随者。同样，定义一个对角矩阵D∈Rn×n为领导者的邻接矩阵，其对角元素为di=ai0。如果节点e0是节点ei的邻居节点，则ai0＞0；否则，ai0=0。其余n个跟随者的系统动态可描述为

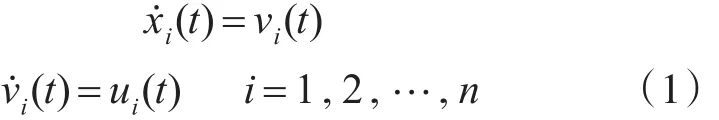
且 初 始 条 件 为 xi(t)=xi(0)，vi(t)=vi(0)，t∈(-∞，0]，其中，xi(t)∈Rn，vi(t)∈Rn分别表示第 i个无人机的位置和速度状态，ui(t)∈Rn为控制协议。

假定领导者的速度为恒定值，它的运动状态是独立的，不受其它节点的影响，而跟随者受领导者和其它跟随者的影响。领导者的状态方程为

其中，x0(t)为领导者的位置，v0为期望的常值速度。

控制协议设计的目的是使跟随者与领导者的位置和速度趋于相同，即多无人机系统（1）达到一致当且仅当无人机的位置和速度变量分别满足：

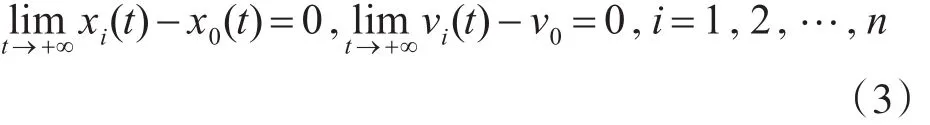
为了解决上述有领导者的二阶多无人机系统的一致性问题，在变拓扑网络结构下，考虑无人机之间的通信时滞和无人机与领导者之间通信时滞不相等的情况，选取如下控制协议：

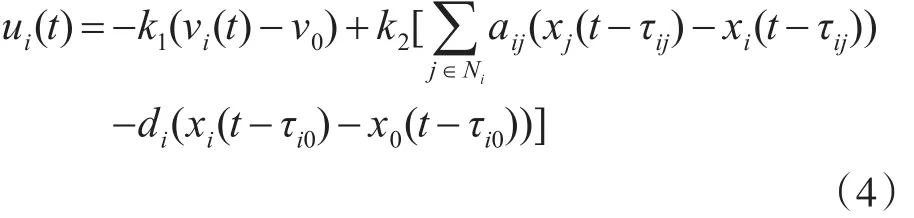
其中，k1＞0，k2＞0为控制参数，aij为有向图边的权值，τ是系统中无人机间的通信时滞，di为领导者邻接矩阵中的元素，且di=ai0。

当无人机之间的通信时滞τij和无人机与领导者之间通信时滞τi0不相等时，设

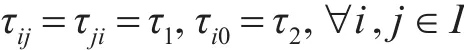
令

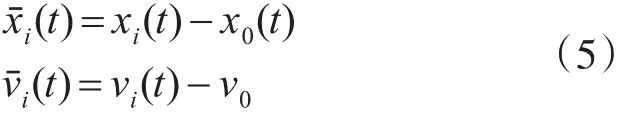
可得

记

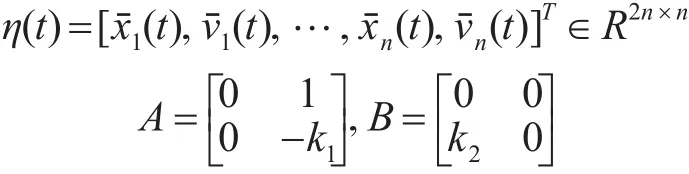
于是，变拓扑网络下系统动态可表示为

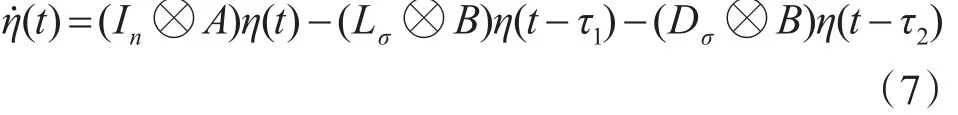
这里Lσ是图G的Laplacian矩阵，Dσ为领导者与跟随者之间的邻接矩阵，‘⊗’表示Kronecker积。

4 带领导者的不同时滞多无人机系统稳定性分析

引理 2［15］设向量 x，y∈Rn，对任意正定矩阵N∈Rn×n，有 2xTy≤xTN-1x+yTNy。

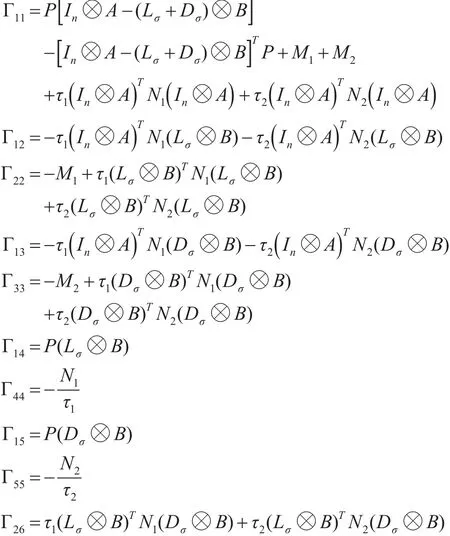
则多无人机系统（7）的状态能够达到一致。其中证明：定义系统（7）的Lyapunov函数如下：

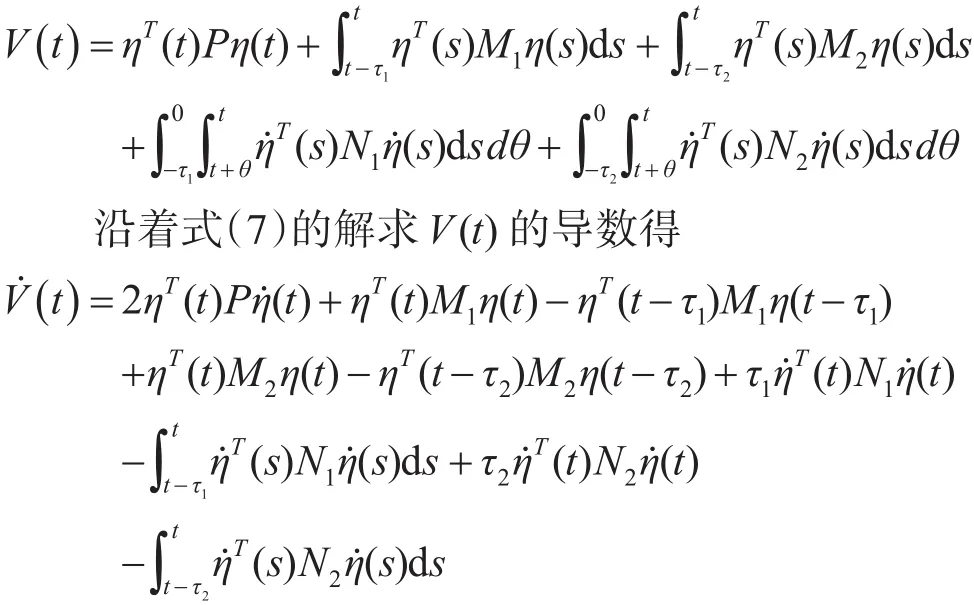
由于V(t)＜0 的充要条件是

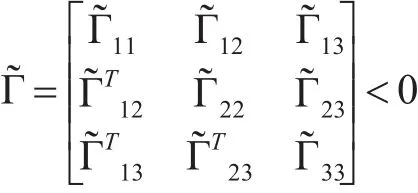
这里

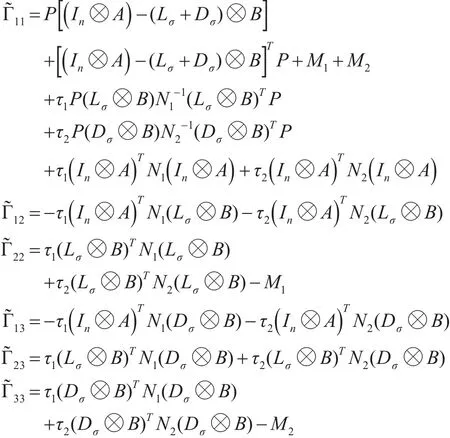
由引理3可知L＜0的充要条件是L＜0。于是，在定理1的条件下有

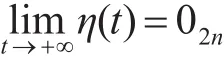
成立，因此系统（7）是渐近稳定的，因此

综上所述，变拓扑网络结构下带领导者的不同时滞多无人机系统（7）可以达到一致。

当无人机之间的通信时滞τij和无人机与领导者之间通信时滞τi0相等时，设

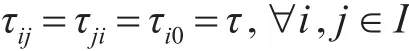
利用控制协议（4），变拓扑网络下系统动态可表示为

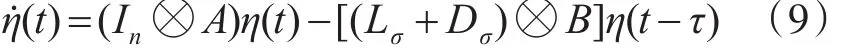
定理2 考虑无人机之间的通信时滞和无人机与领导者之间通信时滞相等的有向切换拓扑网络结构下的二阶多无人机系统，利用控制协议（4），如 果 存 在 对 称 矩 阵 P＞0，M＞0，N＞0 ，且P，M，N∈R2n×2n满足

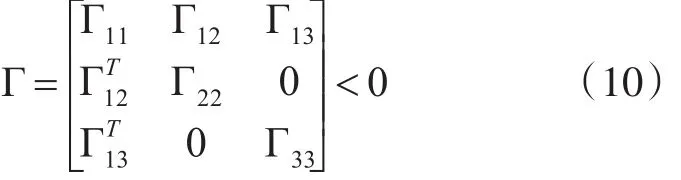
则多无人机系统（9）能够达到一致。其中，

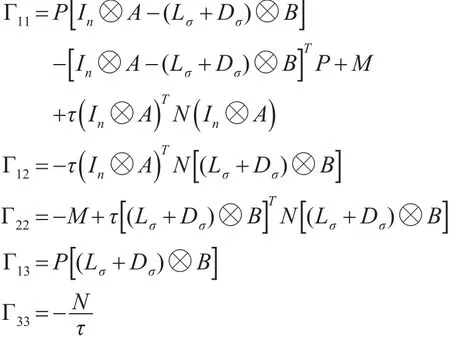
证明：定义系统（9）的Lyapunov函数如下：

沿着式（9）的解求V(t)的导数得

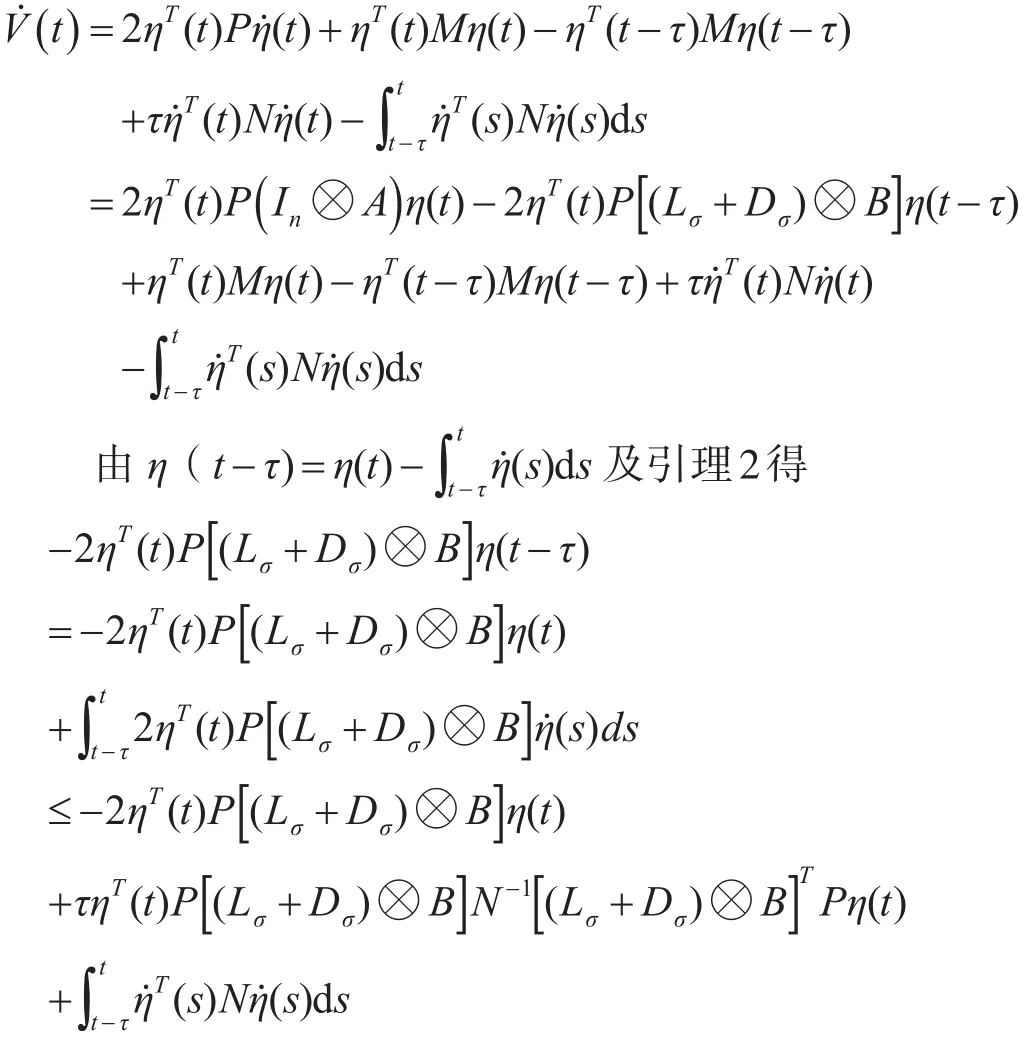
于是

由引理3可知L＜0的充要条件是Γ＜0。于是，在定理1的条件下有

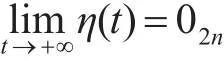
成立，因此系统（9）是渐近稳定的，因此

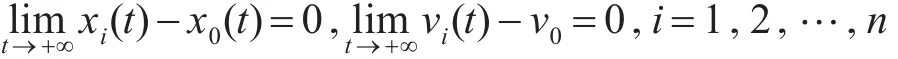
综上所述，切换拓扑网络结构下带领导者的相同时滞多无人机系统（9）可以达到一致。

推论 对于无时滞有向变拓扑网络结构下带领导者的二阶多无人机系统（9），如果存在对称矩阵 P＞0，M＞0，N＞0，且 P，M，N∈R2n×2n满足

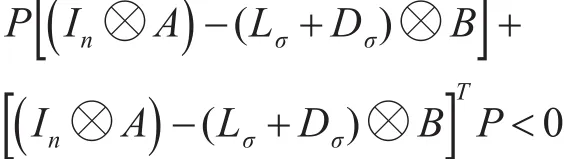
那么，二阶多无人机系统（9）可以达到一致。

5 仿真结果

考虑包含4个无人机的有领导者和时滞的变拓扑有向网络，图1中Ga，Gb，Gc表示三种不同的无人机与领导者的连接拓扑图，节点0为全局可达点，每一边对应的权值为1，图2为拓扑切换图，描述了切换从Ga开始每隔0.02s切换到下一个状态。设领导者的初始状态及期望速度为x0=0，v0=0.2，系统状态的初始值设为

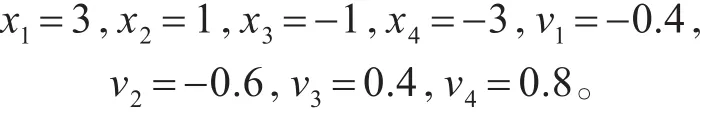
取协议参数k1=k2=1，应用定理2，可知线性矩阵不等式（10）有可行解，并解得系统的最大容许时滞为τ=0.469s。这里取τ=0.3s，变拓扑网络结构下的位置和速度误差曲线分别为图3和图4，所有智能体（无人机）与领导者能够达到渐近一致。此外，对具有不相同时滞的二阶有领导者的多无人机系统进行仿真。依然取k1=k2=1，由定理1，经过计算可得最大不相等时滞分别为τ1=0.435s，τ2=0.583s，图5和图6分别为 τ1=0.2s，τ2=0.4s时变拓扑网络下的位置和速度误差曲线。仿真结果验证了定理1与定理2结论的正确性和有效性。

图1 无人机与领导者的连接拓扑图

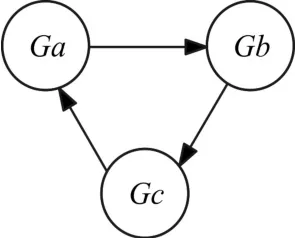
图2 拓扑切换图

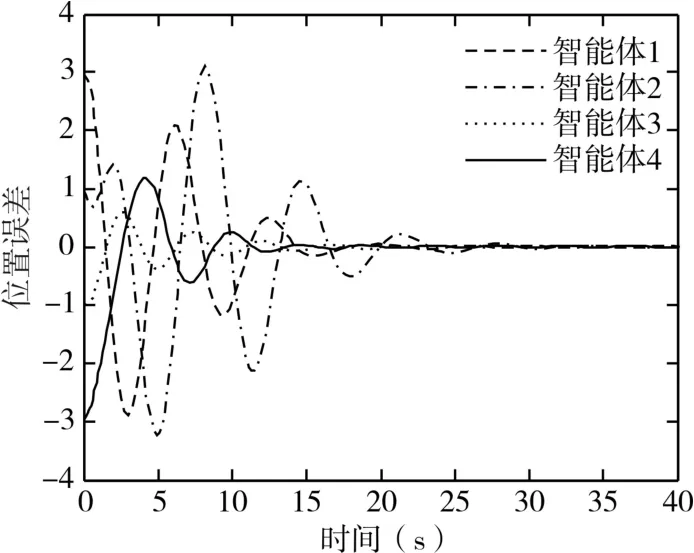
图3 τ=0.3s时位置误差曲线

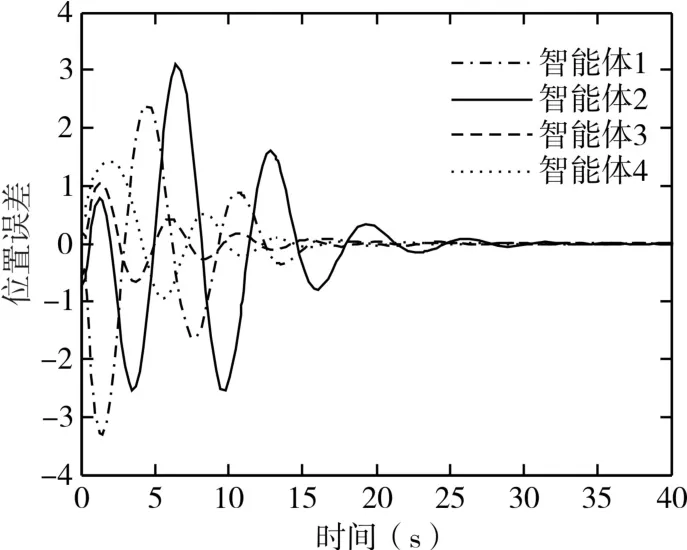
图4 τ=0.3s时速度误差曲线

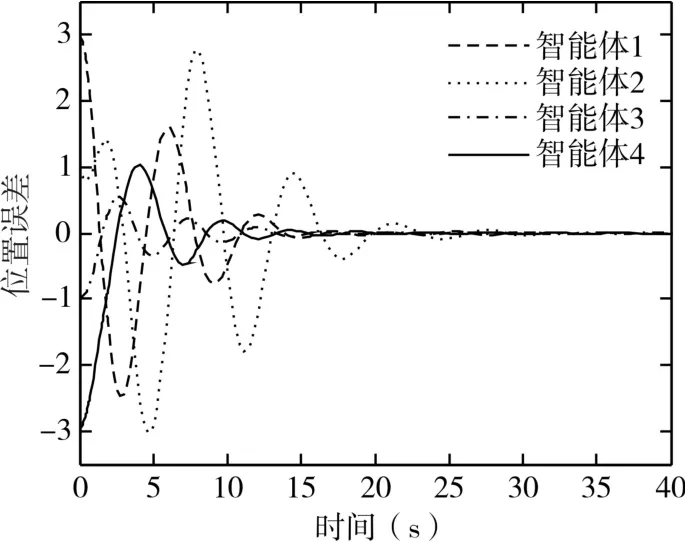
图5 τ1=0.2s，τ2=0.4s时位置误差曲线

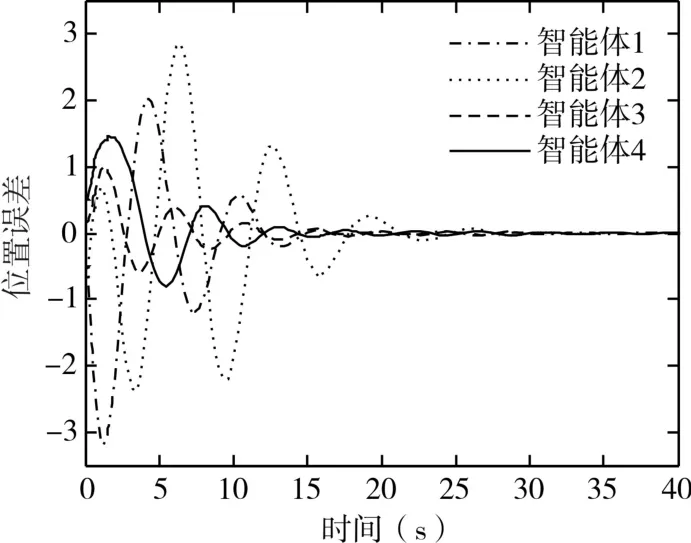
图6 τ1=0.2s，τ2=0.4s时速度误差曲线

6 结语

本文研究了带领导者的不同时滞多无人机系统一致性控制问题。在变拓扑网络结构下，针对无人机间通信时滞和无人机与领导者间通信时滞相同与不同两种情况，采用时域LMI方法得到二阶时滞多无人机系统一致性的充分条件，该条件是以线性矩阵不等式形式给出的，通过解该不等式可以得到时滞的最大容许值。最后，仿真结果验证了所得理论结果的正确性和有效性。本文的研究为下一步进行有领导者的随机时滞多无人机系统的一致性控制问题打下了坚实的基础。

［1］丛一睿.高阶线性多智能体时延一致性理论及其在多无人机协同控制中的应用［D］.长沙：国防科学技术大学，2013.CONG Yirui.High-order Linear Multi-agent Systems Time-delayed Consensus Theory and Its Applications to Multi-UAVs Cooperative Control［D］.Changsha：National University of Defense Technology，2013.

［2］Olfati-Saber R，Murray R.Consensus problems in net⁃works of agents with switching topology and time-delays［J］.IEEE Transactions on Automatic Control，2004，49（9）：1520-1533.

［3］Bliman P，Ferrari-Trecate G.Average consensus problems in networks of agents with delayed communications［C］//Proceedings of the 44th IEEE Conference on Decision Con⁃trol and European Control Conference.Seville，SPAIN：IEEE，2005：7066-7071.

［4］Ren W，Atkins E.Second-order consensus protocols in multiple vehicle systems with local interactions.AIAA Guidance，Navigation，and Control Conference［J］.San Francisco，CA，USA：American Institute of Aeronautics and Astronautics Inc，2005：3689-3701.

［5］Lin P，Jia Y，Du J and Yuan S.Distributed consensus con⁃trol for second-order agents with fixed topology and time-delay［C］//Proceedings of the 26th Chinese Control Conference.Zhangjiajie，P R CHINA：Beijing Univ Aero⁃nautics&Astronautics Press，2007：577-581.

［6］高庆文，樊春霞，韦庆阳.具有随机时延的多智能体系统的一致性研究［J］.计算机技术与发展，2013，23（10）：52-55.GAO Qingwen，FAN Chunxia，WEI Qingyang.Research on ConsensusofMulti-agentSystem with Random Time-delay［J］.Computer Technology and Development，2013，23（10）：52-55.

［7］Sun Y，Wang L.Consensus problems in networks of agents with double-integrator dynamics and time-varying delays［J］.International Journal of Control，2009，82（10）：1937-1945.

［8］ Lin P，Jia Y.Consensus of a class of second-order multi-agent systems with time-delay and jointly-connect⁃ed topologies.IEEE Transactions on Automatic Control，2010，55（3）：778-784.

［9］Xiao F，Wang L，Chen J.Partial state consensus for net⁃works of second-order dynamic agents［J］.Systems&Con⁃trol Letters，2010，59（12）：775-781.

［10］ Liu C，Liu F.Consensus problem of second-order multi-agent systems with time-varying communication delay and switching topology［J］.Journal of Systems En⁃gineering and Electronics，2011，22（4）：672-678.

［11］Liu K，Xie G，Wang L.Consensus for multi-agent sys⁃tems under double integrator dynamics with time-vary⁃ing communication delays［J］.International Journal of Robustand NonlinearControl，2012，22 （17） ：1881-1898.

［12］Ou M，Du H，Li S.Robust consensus of second-order multi-agent systems with input and time-varying commu⁃nication delays［J］.International Journal of Modelling，Identification and Control，2012，17（4）：285-294.

［13］欧美英，谷胜伟，董可秀.具有时变时延的二阶多智能体系统在有向拓扑下的一致性问题［J］.中国科学技术大学学报，2015，45（10）：871-880.OU Meiying，GU Shengwei，DONG Kexiu.Consensus of second-order multi-agent systems with directed topolo⁃gies and time-varying delays［J］.Journal of University of Science and Technology of China，2015，45（10）：871-880.

［14］邵俊倩，栾孟杰，张岩.有leader的二阶时滞多智能体系统一致性分析［J］.兰州理工大学学报，2015，4（4）：90-94.SHAO Juqian，LUAN Mengjie，ZHANU Yan.Consensus analysis of second-order multi-agent systems with leader and time-delay［J］.Journal of Lanzhou University of Technology，2015，4（4）：90-94.

［15］De Souza Carlos E.，Li Xi.Delay-Dependent Robust H∞Control of Uncertain Linear State-Delayed Systems［J］.Automatica，1999，35（7）：1313-1321.

［16］贾英民.鲁棒H∞控制［M］.北京：科学出版社，2007.144-145.JIA Yingmin.Robust H∞ Control［M］.Beijing：Science Press，2007.144-145.

Formation Control of Multi-UAVs System With One Leader and Different Time-Delay

SHAO Junqian LI Chengfeng SUN Jian
（College of Information Engineering，Suihua University，Suihua 152061）

Based on consistency theory of Multi-agent systems with time-delay，the formation control problem is studied for multi-UAVs system with one leader and different time-delay.Control protocol of the system is Improved，it make multi-UAVs sys⁃tem in the case of a few information to ensure consensus.In the network with switching topology，the time domain linear matrix in⁃equality（LMI）method is employed，suffcient condition in terms of LMI is derived to ensure consensus of second order multi-UAVs system，which can provide the allowable upper bound of time-delay.Further communication time-delay among unmanned aerial ve⁃hicles is equal to communication time-delay between unmanned aerial vehicle and the leader that condition is discussed，and a sim⁃ulation example is provided to show the effectiveness of controllers design.

multi-UAVs system，communication time-delay，controller，consistency theory

Class Number TP18

TP18

10.3969/j.issn.1672-9722.2017.12.013

2017年6月28日，

2017年7月29日

黑龙江省绥化市科技计划项目（编号：SHKJ2015-017）；绥化学院杰出青年基金项目（编号：SJ15005）资助。

邵俊倩，女，硕士，讲师，研究方向：多智能体系统协调控制。李成凤，女，硕士，讲师，研究方向：多智能体系统协调控制。孙剑，女，硕士，副教授，研究方向：多智能体系统协调控制。