对传统几种组卷算法改进与比较分析∗

张亚妮

（宝鸡职业技术学院 宝鸡 721013）

对传统几种组卷算法改进与比较分析∗

张亚妮

（宝鸡职业技术学院 宝鸡 721013）

组卷算法也是网络考试系统中的关键问题之一，论文在组卷算法方面也进行了一定的研究，实现了一种改进的随机算法和遗传算法，并对算法的实际效果进行了比较分析。

遗传算法；智能组卷

1 引言

自动组卷是考试系统自动化或半自动化操作的核心目标之一，而如何保证生成的试卷最大程度地满足用户的不同需要，并且具有随机性、科学性、合理性，这是现实中的一个难点［1］。尤其在交互式环境下用户对于组卷速度要求较高，题目应具有多样性、不宜作弊等，因此一个良好的组卷系统对于考试来说起着非常重要的作用［2］。组卷算法是网络考试系统的核心功能之一，一个优秀的组卷算法决定了考试系统的实用性。本文分析多种组卷算法并对其进行改进，使得用户能够根据不同的考试要求和题库模式选择最适合的组卷算法。

2 改进的随机算法

结合一般的随机算法与贪心算法的思想，在组卷过程中可以避免完全盲目的抽题、试验［3］。在抽题过程中，可以充分利用已经选取题目的信息，辅助抽取后面的题目。具体的做法是引入贪心算法的思想，在选取下一道试题时，总是去抽取最能满足当前约束条件的试题。算法的关键就什么样的题目是最能满足当前约束条件的题目以及如何与现有约束条件结合来确定这样的题目［4］。

试卷的约束条件是一个二维矩阵，已选取的题目同样能组成一个对应的二维矩阵，可将该矩阵成为当前约束条件矩阵［5］。初始时，已选题目数为0，当前约束条件矩阵中的元素也全部都是0。随着组卷过程的进行，矩阵元素的值是不断累加的。在理想的情况下，最终的当前约束条件矩阵应该与目标约束矩阵是完全一致的。

初始当前约束条件矩阵：

组卷过程中的当前约束条件矩阵：

将试卷的目标约束矩阵与当前约束矩阵做矩阵减法运算，将得到的矩阵称之为目标差矩阵。

某一时刻的目标差矩阵：

从另一面来想，每选定一道题目，该矩阵中就会有些元素的值减小，组卷的过程就是不断地让这个目标差矩阵累减为0的过程。这里就可以结合贪心算法的思想，每选一道题目时，都尽量使得矩阵中尽可能多的元素值和尽可能大的元素值减小，这便是组卷过程中的局部最优。上面的示例矩阵只是为了表述方便，实际上，在组卷过程中矩阵中元素的值是均匀地减小的，目标差矩阵不会出现同一约束条件中一些值特别大获特别小的情况。

具体实施时，从得到的目标差矩阵中，找出每一个约束条件上值最大的一个，其对应的状态空间可以组成一个一维的矩阵，如在上面的示例中，得到的一维矩阵将是［单选，较易，了解，知识点3，小节5］，而这个矩阵就是最能满足当前约束条件的题目所应该满足的条件，符合这个条件的题目就是当前的局部最优解。因为在约束条件矩阵中，每一行代表了一个约束条件，而当前题目矩阵的每一行是该约束的当前满足情况，那么目标差矩阵中每一行的最大值，就是该约束条件中最亟需满足的。在选取题目时，优先选择满足这个差距最大的值，以使目标差矩阵尽快地趋进于0，从而选定题目尽快地趋近给定约束矩阵。这时选取每一道题目时就带有很强的目的性，在满足这个一维矩阵条件情况下的题目中随机选择一道。因为在每一个约束条件上都是差距最大的，一次选题的成功率会明显提高。在理想的情况下，整张试卷的题目能够一次选题成功，其选题效率的提高是显而易见的。

3 改进遗传算法

有很多人已经研究过采用遗传算法来解决组卷问题，用基本的遗传算法解决组卷问题，会产生早期的盲目搜索、过早收敛、收敛于局部最优解、局部搜索能力不强等弊病，这是由传统遗传算法的缺陷造成的［6］。在组卷应用中可以对遗传算法进行改进，采用整数编码和竞争选择方法［7］。这种方法不仅避免了遗传算法中经常出现的“早熟现象”，而且有效地解决了智能组卷中的约束优化问题，具有很好的性能和实用性。在求解时，关键完成以下几个方面：

1）确定编码方案

一份试卷就是组卷算法的一个最终可行解，因此将一份试卷映射成一个染色体，每个试题映射为染色体中的基因。通常情况下，基因的值用试题在题库中的题号表示，因为在实际实现中将采用面向对象的模型构建算法，基因的值就可以是一个试题的元数据对象，而试题在试题库中的编号作为一个试题的标识。这样一个染色体的编码可表示为：{q1，q2，…，qm}，式中 qi为试题的题号或者一个试题的元数据对象，且同种题型的试题编号组在一起形成段，每一段反映一个题型：

{(q1，q2，…，qm)，(qm+1，qm+2，…，qm+p)，…，(…)}

在一个染色体中，每一段长度由约束条件中该题型的数量决定；在试题库中每一段长度由题库内该题型的数量决定。这样易于用面向对象的模型实现，克服了二进制编码的编码、解码的过程，明显缩短了求解时间，在进化时表现出很好的搜索性能。

2）初始群体的生成

组卷算法的初始群体并不是完全随机生成的，而是根据某一个较强的约束条件，来确定初始群体。在编码方案中，根据题型将试题也就是基因分成了不同的段，因此在初始化群体时也是根据题型分别初始化染色体的每一段，使得初始化后群体中的每一个染色体根据题型约束自然分段。这个划分也为简化后面的进化操作奠定了基础。

根据组卷约束条件中题型分布的要求，计算出各类型的试题应该抽取的数目，随机在题型相同但其他条件任意的试题库子集中抽取试题组成一个染色体，然后重复此过程，直到达到事先指定的种群规模，这些染色体构成了初始群体。

在一些组卷算法中，通过在抽取试题的过程中在题库中设置标志位，来避免同一个染色体和不同染色体之间中出现重复试题的情况。但是这样在同一时刻只能进行一套试卷的抽题操作，即使不在原题中设置标志位，也会增加访问题库的频率，影响种群初始化的速度。因此在多人在线考试系统中，这并不是一种十分理想的做法［8］。利用随机函数在一定程度上保证生成的初始个体将均匀地分布在整个解空间上，并保证随机产生的各个体间有明显的差距、初始群体含有较丰富的模式、增强了搜索收敛于全局最优点的可能［9］。同时，在后面的进化操作中，要避免新的染色体中出现相同试题。

通过这个初始化操作，每个染色体时间上都已经满足了一个约束条件——题型，因此在后面的进化操作中就可以省去题型这个约束条件。

3）适应度函数的确定

在遗传算法中，以适应度函数的大小来区分群体中个体的优劣一般情况下，适应度函数是由目标函数变换而成的，其值越大个体越好，对前面的组卷模型来说是最小化问题［10］。在组卷的适应度函数中，应该计算染色体的整体适应度，要同时考虑组卷的各个指标，使得组卷的各项指标均向要求的值收敛。

4）遗传操作

遗传操作主要包括交叉、变异和选择3个操作，这3个操作也称为遗传算子，遗传算子决定了群体的进化行为。

（1）优选父代自适应交叉操作。算法在进行交叉操作时，提高被交叉父代个体的质量，以期望产生高质量的子代。具体操作为：从上代群体中随机选择两个个体，保留适应值大的个体（如二者适应值相同，则随机保留一个），再进行一次上述两两优选操作。对保留下来的两个个体进行交叉。交叉采用二进制编码遗传算法中的多点交叉方式，且规定交叉在两个个体的各个相同题型段内同时进行。

交叉概率采用改进式自适应方式产生，采用改进式不但在进化后期表现良好，而且在进化初期提高群体中表现优良个体的交叉率，使得它们不会处于一种近似停滞不前的状态，降低进化走向局部最优解的可能性。改进式自适应交叉概率由下式确定：

式中：Fc为要交叉的两个串中较大的适应值；Fmax、Favr为上代群体中个体的最大适应值及群体的平均适应值；pc1=0.9，pc2=0.6。

（2）自适应变异操作。变异采用段内单位置替换式变异，即在个体的各个不同题型段内随机选取一位进行替换，且规定该位被替换后的试题不能与该个体的其他位试题重复。变异概率采用改进式自适应变异概率，使变异在进化初期和后期都有很好的表现，其具体表达式为

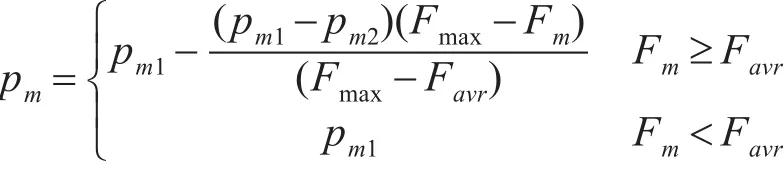
式中Fmax、Favr为上代群体中个体的最大适应值及群体的平均适应值；Fm为要变异个体的适应值；pm1=0.1，pm2=0.001。

（3）选择操作。为了保证搜索达到的最佳个体不会被各种遗传操作破坏，并保留上代群体的优良特性，算法把上代群体全部复制并保留到匹配池中。

5）终止条件

组卷系统可以采用下面3种类型的停止标准：最简单的标准是在固定进化次数后停止。另一种停止标准是基于群体中收敛的程度。即已生成的所有个体的平均适应度与最好个体的平均适应度的比 ≥0.99则算法终止。第三种停止标准是算法执行一段时间后，如果没有新的更好解产生，则停止。

4 实验结果及分析结论

本网络考试系统采用Java语言编写，实现了随机和遗传2种组卷算法，并利用中华人民共和国卫生部测试题库进行了算法测试。为了便于对算法进行对比测试，测试版的软件同时给出了随机算法和遗传算法组卷的入口。

题库中共有试题3875道试题，在题型、难度、认知层次等试题属性上的分布情况如表1所示。

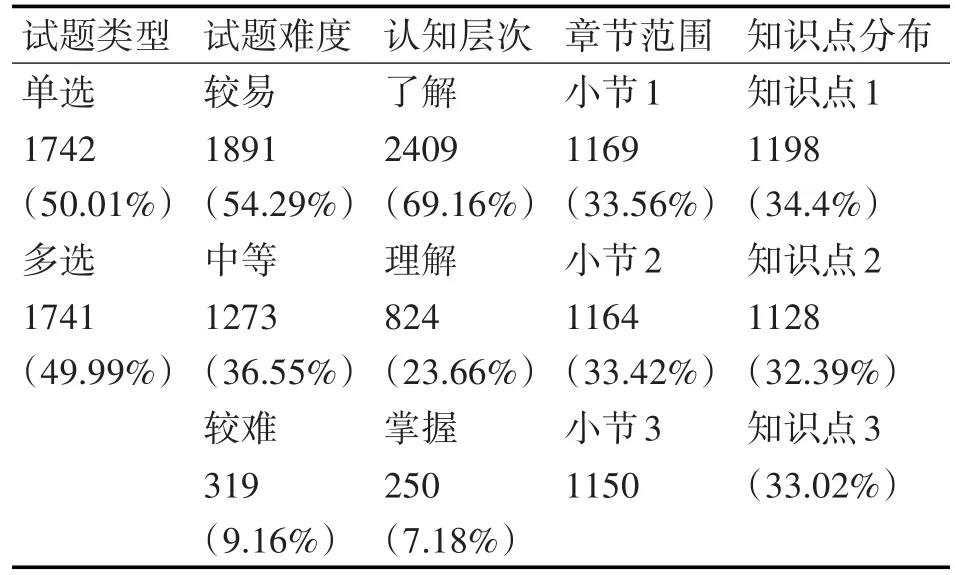
表1 试题库状态分布

试验的软硬件环境分别为：操作系统：Window 2003 Server；Web 服务器：Tomcat5.0.29；数据库：MySQL 4.1；PC 机：一台；CPU：迅驰 1.4G；内存：768M；Web服务器和数据库服务器位于同一台PC机上。

当试卷要求题目总数为20道，只有题型、难度和认知层次3个约束条件下，具体约束条件如表2。

表2 组卷约束条件

随机算法得到的组卷结果如表3，用时0.431s。

表3 随机算法组卷结果

遗传算法得到的组卷结果如表4，用时35.15s。

表4 遗传算法组卷结果

当试卷要求题目总数为40道题时，得到的组卷结果与以上基本一致，随机算法用时增加到0.93s，遗传算法在种群规模60迭代代数为40的情况下用时增加到57.77s。

在同样的条件下40道题，分别对随机算法和遗传算法连续测试20次，得到的组卷结果与以上一致。随机算法平均用时0.9s，遗传算法平均用时55s。

当试卷要求题目总数为60道，约束条件包括题型、难度、认知层次、知识点分布、章节分布5个条件，具体约束条件如表5。

表5 组卷约束条件

遗传算法得到的测试结果如表6，用时72.0s。

表6 遗传算法组卷结果

将种群规模和迭代代数都增加到60时，遗传算法得到的结果如表7。

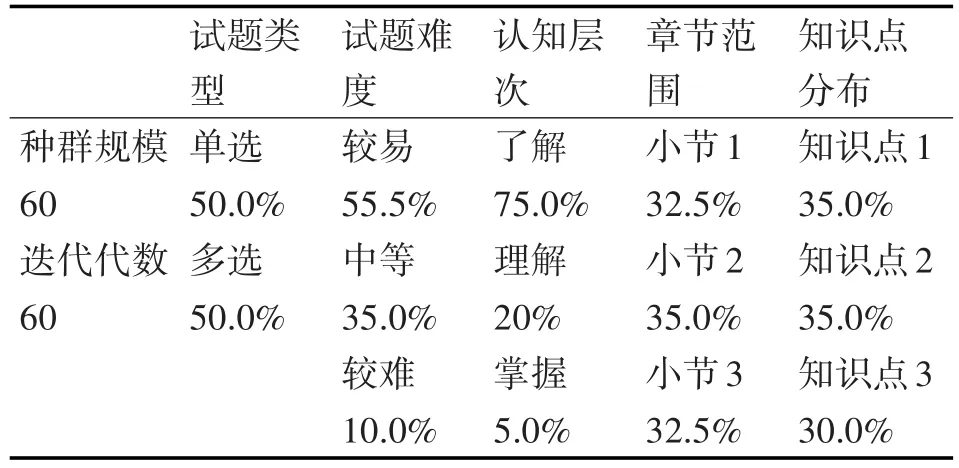
表7 遗传算法组卷结果

在5个约束条件下抽取60道题目，分别对随机算法和遗传算法连续测试20次，组卷结果的平均情况与以上结果基本一致，随机算法平均用时1.4s，遗传算法平均用时75s。

测试结果表明，随机算法与遗传算法哪个效率高并不是绝对的，随着约束条件的改变，各自的表现也有所不同。

加入了贪心算法思想的随机算法在组卷速度上有着明显的优势。当约束条件较少，试卷要求的题目数量与题库题目数量相比是很少时，其组卷的各项指标都能够100%地达到要求的约束，用时也极少，最少的不足1s，最多也不过5、6s。当约束条件扩充时，用时上并没有增加许多，但是组卷质量却有所下降。这是因为算法在最后无法找到最合适的题目时会削弱约束条件，以保证组卷成功，这时组出的试卷各项指标并不是与约束条件完全吻合的。多次试验也表明，约束增加后试卷之间重复题目的数量也开始增多，试题的随机性显著下降。

遗传算法在约束条件较少、试卷要求的题目数也较少时，并没有显示出明显的优势，甚至在组卷速度上用时是随机算法的好几十倍。但是随着约束条件的增加以及试卷题目数量的增加，遗传算法在组卷质量上要好于随机算法。试卷的质量表现在，虽然有很多试卷指标与要求的约束没有达到100%的吻合，但是差距与要求的约束相差很小，都在可以接受的范围之内。这是因为遗传算法每次进化都并行的考虑所有约束条件，并在全局范围内寻优，使得各项指标都能均匀地向要求的约束收敛。同时，遗传算法还有一个优势就是一次同时组出多份满意的试卷。除种群最好的个体外，排在前几位的次好好个体也基本上能够满足要求。

5 结语

综上所述，随机算法和遗传算法在组卷中的应用都有相应的优势和不足，选用哪一种算法并不是绝对的。在实际应用当中，算法的选择应该根据试卷的约束情况、题库中题目数量和题目的分布情况以及对试卷指标的误差定义来决定。

［1］Zhouguobing，Liutingting，Liu，et al.Algorithm and strat⁃egy research of generating test paper for large scale online examination［C］//International Conference on Electronic and Mechanical Engineering and Information Technology，Emeit 2011，Harbin，Heilongjiang，China，12-14 August.2011：3285-3288.

［2］ Mei Y，Cheng L.Scoring Fairness in Large-Scale High-Stakes English Language Testing：An Examination of the National Matriculation English Test［M］//English Language Education and Assessment：Recent Develop⁃ments in Hong Kong and Chinese Mainland，2014：171-187.

［3］Yang C Y，Li Z Y，Gu Y D，et al.A Study on Improving Methods of Multi-Source and Multipath in Large-Scale Examination System Cloud Environment［J］.Applied Me⁃chanics&Materials，2014，687-691：2722-2727.

［4］Yu F，Liu W，Cui M.Heuristic Genetic Test Paper Algo⁃rithm for Online Examination System［J］.Advanced Mate⁃rials Research，2013，798-799：676-679.

［5］Tang H T.Strategy for Test Paper Composition Based on Genetic Algorithm［J］.Applied Mechanics&Materials，2014，513-517（513-517）：1688-1691.

［6］Tang C S，Dong Y D，Xiong R.Algorithm for random creat⁃ing test papers online and its realization［J］.Journal of He⁃fei University of Technology，2006，29（3）：296-299.

［7］Huang B L.Application of Adaptive Genetic Algorithm in Intelligent Test Paper Composition［J］.Computer Engi⁃neering，2011，37（14）：161-163.

［8］Li X，Wang Z，Wu X，et al.The design of adaptive test pa⁃per composition algorithm based on the item response theo⁃ry［C］//Information Technology and Artificial Intelligence Conference.IEEE，2011：157-159.

［9］Chang T Y，Ke Y R.A personalized e-course composition based on a genetic algorithm with forcing legality in an adaptive learning system［J］.Journal of Network&Com⁃puter Applications，2013，36（1）：533-542.

［10］Chang T Y，Ke Y R.A personalized e-course composi⁃tion based on a genetic algorithm with forcing legality in an adaptive learning system［J］.Journal of Network&Computer Applications，2013，36（1）：533-542.

Analysis of Several Groups of Traditional Algorithm Improvement and Comparative

ZHANG Yani
（Baoji Professional Technology Institute，Baoji 721013）

Group algorithm also is one of the key issues in the network examination system，This paper has conducted the group algorithm research，achieved an improved random algorithm and genetic algorithm，and analyzed the actual effect of the algo⁃rithm.

genetic algorithms，smart group volume

Class Number TP301

TP301

10.3969/j.issn.1672-9722.2017.12.009

2017年6月5日，

2017年7月27日

张亚妮，女，硕士，讲师，研究方向：计算机应用技术。